当前位置：首页 > news >正文

树上LCA和树链剖分（未完待续）

news 2025/9/23 7:21:31

一、树上最近公共祖先

树上最近公共祖先简称 LCA，在有根树里面，两个结点的 LCA 指的是两者往根节点爬的过程中路径第一次重合的那个结点。

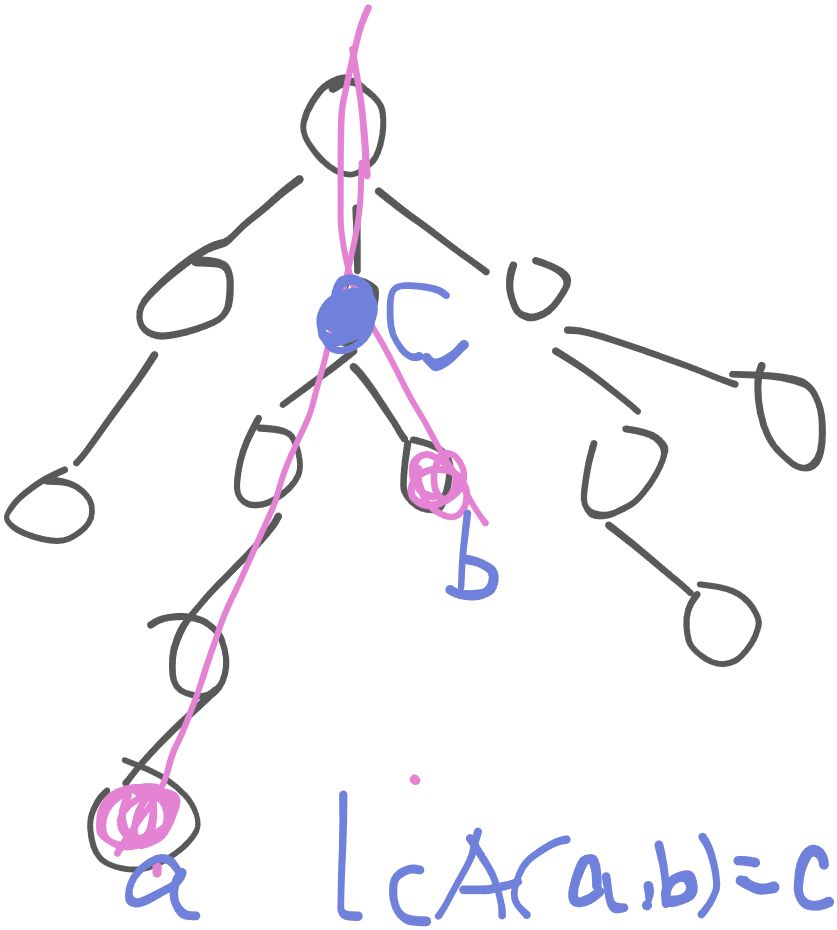
LCA 具有以下几个性质：

LCA(x) = x，即一个结点的最近公共祖先是自己。
如果 x 是 y 的祖先，那么 LCA(x, y) = x。
如果 x，y 并不是对方的祖先，那么 x，y 分别位于 LCA(x, y) 的两棵不同的组数中。
记 S 为树中的点集。前序遍历中，LCA(S) 出现在所有结点之前，后续遍历中，LCA(S) 出现在所有结点的最后。
LCA(x, y) 一定在 x，y 的简单路径上.
记 A，B 为树中两个点集，那么 LCA(LCA(A), LAC(B)) = LCA(A ∪ B)。
两点简单路径长度为 d(x, y) = d(x, r) + d(y, r) - 2 * d(r, LCA(x, y))。

（一）、朴素解法

向上标记法：两个节点分别往上走，标记途径的结点，第一次相遇的位置即为所求的LCA。

时间复杂度：如果没有告知父节点，预处理父节点的时间复杂度为O（n）。针对于每次的查询，最坏情况下会遍历整个树一次，为O（n）。

如果多次查询LCA，时间复杂度是O（qn），效率较慢。

（二）、树上倍增

利用倍增的思想，优化朴素解法，类似于st表。

树上倍增需要准备以下数组：

f[x][i]：表示 x 结点往上跳 2^i 次方步后所能到达的结点。
dep[x]：表示 x 结点的深度。

这两个信息我们都可以通过一次 dfs 遍历

f[x][i] = f[f[x][i - 1]][i]。
dep[x] = dep[fa] + 1。
f[x][0] = fa。

预处理的时间复杂度为O（logn）

#include <iostream>
#include <vector>
using namespace std;
const int N = 5e5 + 10, M = 25;
int dep[N], f[N][M];
vector<int> edges[N];void dfs(int x, int fa)
{dep[x] = dep[fa] + 1;f[x][0] = fa;for(int i = 1; i <= 20; i++)f[x][i] = f[f[x][i - 1]][i - 1];for(auto y : edges[N]){if(y == fa) continue;dfs(y, x);}
}

下面我们还需要实现几个操作：

让 x 向上爬到 y 层。

void up(int x, int y)
{for(int i = 20; i >= 0; i--){if(dep[f[x][i]] >= y) // 本质上是枚举 y - x 的二进制{x = f[x][i];}}
}

（三）、LCA

求解 LCA 的思路

让 x， y 结点同层。
x，y 一起往上爬，爬到 lca(x, y) 的的下一个结点。

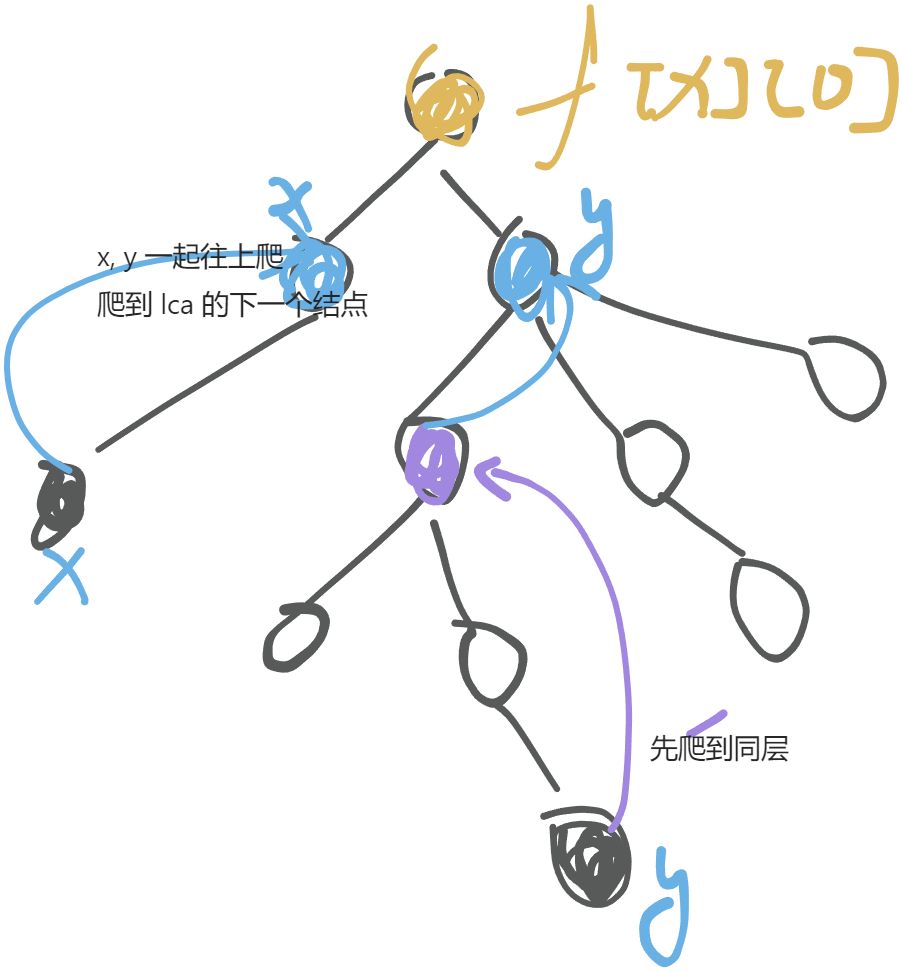
【模板】最近公共祖先（LCA）

#include <iostream>
#include <vector>
#include <unordered_map>
#include <map>
#include <unordered_set>
#include <set>
#include <algorithm>
#include <cmath>
#include <string>
#include <cstring>
#include <queue>
#include <cstring>using namespace std;
#define endl '\n'
typedef long long LL;
typedef pair<int, int> PII;
#define lc p << 1
#define rc p << 1 | 1
#define lowbit(x) (x & -x)
const int N = 5e5 + 10, M = 25;
const LL MOD = 1e9 + 7;
const double ln2 = log(2);
const double rec_ln2 = 1.0 / ln2;
int f[N][M]; // f[x][i]：表示 x 结点往上走 2 ^ i 步走到的结点
int dep[N]; // dep[x]：x 结点的深度
int n, m, s;
vector<int> edges[N];void dfs(int x, int fa)
{dep[x] = dep[fa] + 1;f[x][0] = fa;for(int i = 1; i <= 20; i++)f[x][i] = f[f[x][i - 1]][i - 1];for(auto y : edges[x]){if(y == fa) continue;dfs(y, x);}
}int lca(int x, int y)
{if(dep[x] < dep[y]) swap(x, y); // 让高度低的往上跳for(int i = 20; i >= 0; i--){if(dep[f[x][i]] >= dep[y]){x = f[x][i];}}if(x == y) return x; // y 是 x 的祖先for(int i = 20; i >= 0; i--){if(f[x][i] != f[y][i]){x = f[x][i];y = f[y][i];}}return f[x][0];
}void solve()
{cin >> n >> m >> s;for(int i = 1; i <= n - 1; i++){int u, v; cin >> u >> v;edges[u].push_back(v);edges[v].push_back(u);}dfs(s, 0);while(m--){int a, b; cin >> a >> b;cout << lca(a, b) << endl;}
}int main()
{cin.tie(0), cout.tie(0), ios::sync_with_stdio(false);int T = 1;// cin >> T;while(T--){solve();}return 0;
}

时间复杂度：

预处理：O（n * logn）
每次查询：O（logn）

（四）、tarjin 算法

tarjin 算法是一种离线算法，巧妙的利用并查集一次查询出大量的lca。但需要注意离线操作只能线下查询，并不能在线操作。

下面是tarjin 算法的流程，算法中操作的顺序：

在某个点回溯之后，把这个结点所在的集合，合并到父节点所在的集合。
递归完成以某个点为根节点的子树后，往上回溯之前，查询相关操作，如果查询的另一个点已经遍历遍历完成，这个点所在集合的代表元素就是两者的 lca。

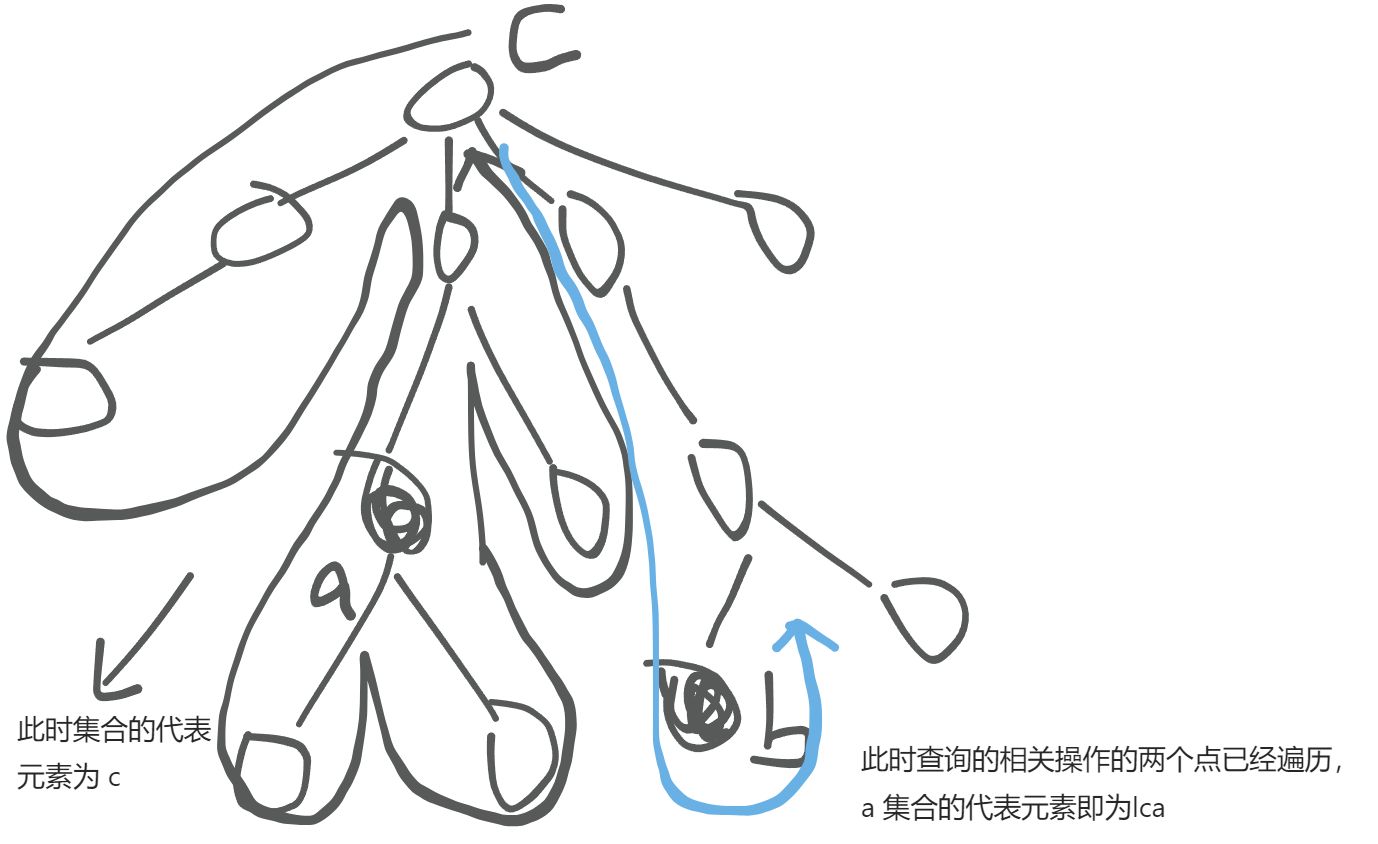
tarjin 算法的正确性可以感性理解以下，当 y 不是 x 的父节点时，x， y 位于 lca 的两颗子树中，递归遍历lca的子树时，会先把先出现那一个结点先挂到 lca 上，在该子树没有遍历完前，这个代表元素不会改变，这样当查到另一个结点的时候，x 所在集合的代表元素正好是他们的lca。

tarjin 算法的流程：

从根节点开始dfs；
进入时，打上已经遍历的标记，st[x]=true
枚举的孩子y，如果没有访问过，遍历 y。
回溯时，将这个子树上的点合并到上， fa[y]=x
递归完以为根的子树，向上回溯时，更新结果。枚举以为x起点的查询： (x,y)
- 如果被搜索过，则所在并查集的根结点就是的LCA(x, y)；
- 如果没有被访问过，那么这个查询会在遍历到结点的时候再去更新结果 ;

code：

#include <iostream>
#include <vector>
#include <unordered_map>
#include <map>
#include <unordered_set>
#include <set>
#include <algorithm>
#include <cmath>
#include <string>
#include <cstring>
#include <queue>
#include <cstring>using namespace std;
#define endl '\n'
typedef long long LL;
typedef pair<int, int> PII;
#define lc p << 1
#define rc p << 1 | 1
#define lowbit(x) (x & -x)
const int N = 5e5 + 10;
const LL MOD = 1e9 + 7;
const double ln2 = log(2);
const double rec_ln2 = 1.0 / ln2;
int n, m, s;
bool st[N];
vector<PII> query[N]; // 离线处理查询，和 i 有关的所有操作
int ans[N]; // 答案
int fa[N]; // 并查集
vector<int> edges[N];int find(int x)
{return fa[x] == x ? x : fa[x] = find(fa[x]);
}void tarjin(int x, int f)
{st[x] = true;for(auto y : edges[x]){if(st[y]) continue;tarjin(y, x);fa[y] = x; // 回溯之后}// 回溯之前for(auto& [y, i] : query[x]){if(st[y]) ans[i] = find(y);}
}void solve()
{cin >> n >> m >> s;for(int i = 1; i <= n; i++) fa[i] = i;for(int i = 1; i <= n - 1; i++){int u, v; cin >> u >> v;edges[u].push_back(v);edges[v].push_back(u);}for(int i = 1; i <= m; i++){int a, b; cin >> a >> b;query[a].push_back({b, i});query[b].push_back({a, i});}tarjin(s, 0);for(int i = 1; i <= m; i++) cout << ans[i] << endl;cout << endl;} int main()
{cin.tie(0), cout.tie(0), ios::sync_with_stdio(false);int T = 1;// cin >> T;while(T--){solve();}return 0;
}

时间复杂度：做出询问为O（1），预处理为O（n + m）

（五）、最近公共祖先练习题

1.「一本通 4.4 练习 1」Dis

题目描述：给出 n 个点的一棵树，多次询问两点之间的最短距离。

注意：边是双向的。

【解题】：x, y两点间的最短距离简单路径上的边权和，求出两点的最近公共祖先c，答案为dist[x] + dist[y] - 2 * dist[c]。

code：

#include <iostream>
#include <vector>
#include <unordered_map>
#include <map>
#include <unordered_set>
#include <set>
#include <algorithm>
#include <cmath>
#include <string>
#include <cstring>
#include <queue>
#include <cstring>using namespace std;
#define endl '\n'
typedef long long LL;
typedef pair<int, int> PII;
#define lc p << 1
#define rc p << 1 | 1
#define lowbit(x) (x & -x)
const int N = 1e4 + 10, M = 25;
const LL MOD = 1e9 + 7;
const double ln2 = log(2);
const double rec_ln2 = 1.0 / ln2;
int n, m;
vector<PII> edges[N];
int dep[N], f[N][M], dist[N];void dfs(int x, int fa)
{dep[x] = dep[fa] + 1;f[x][0] = fa;for(int i = 1; i <= 20; i++)f[x][i] = f[f[x][i - 1]][i - 1];for(auto& [y, w] : edges[x]){if(y == fa) continue;dist[y] = dist[x] + w;dfs(y, x);}
}int lca(int x, int y)
{if(dep[x] < dep[y]) swap(x, y);for(int i = 20; i >= 0; i--){if(dep[f[x][i]] >= dep[y]){x = f[x][i];}}if(x == y) return x;for(int i = 20; i >= 0; i--){if(f[x][i] != f[y][i]){x = f[x][i];y = f[y][i];}}return f[x][0];
}void solve()
{cin >> n >> m;for(int i = 1; i <= n - 1; i++){int u, v, k; cin >> u >> v >> k;edges[u].push_back({v, k});edges[v].push_back({u, k});}dfs(1, 0);while(m--){int x, y; cin >> x >> y;cout << dist[x] + dist[y] - 2 * dist[lca(x, y)] << endl;}
}int main()
{cin.tie(0), cout.tie(0), ios::sync_with_stdio(false);int T = 1;// cin >> T;while(T--){solve();}return 0;
}

2. 商务旅行

题目描述：有 N 个城镇，首都编号为 1。商人从首都出发，其他各城镇之间都有道路连接。

任意两个城镇之间如果有直连道路，在他们之间行驶需要花费单位时间。如果从首都出发，能到达任意一个城镇。

请你求出商人最短的旅行时间。

【解题】：商人从 x 走到 y 走的是 x->y 的简单路径，初始位置在 cur = 1 结点，随后依次对每个结点求与前面所在结点的LCA，累加路径 dep[cur] + dep[x] - 2 * dep[LCA(cur, x)]。

#include <iostream>
#include <vector>
#include <unordered_map>
#include <map>
#include <unordered_set>
#include <set>
#include <algorithm>
#include <cmath>
#include <string>
#include <cstring>
#include <queue>
#include <cstring>using namespace std;
#define endl '\n'
typedef long long LL;
typedef pair<int, int> PII;
#define lc p << 1
#define rc p << 1 | 1
#define lowbit(x) (x & -x)
const int N = 3e4 + 10, M = 25;
const LL MOD = 1e9 + 7;
const double ln2 = log(2);
const double rec_ln2 = 1.0 / ln2;
int n, m;
vector<int> edges[N];
int dep[N], f[N][M];void dfs(int x, int fa)
{dep[x] = dep[fa] + 1;f[x][0] = fa;for(int i = 1; i <= 20; i++){f[x][i] = f[f[x][i - 1]][i - 1];}for(auto y : edges[x]){if(y == fa) continue;dfs(y, x);}
}int lca(int x, int y)
{if(dep[x] < dep[y]) swap(x, y);for(int i = 20; i >= 0; i--){if(dep[f[x][i]] >= dep[y]){x = f[x][i];}}if(x == y) return x;for(int i = 20; i >= 0; i--){if(f[x][i] != f[y][i]){x = f[x][i];y = f[y][i];}}return f[x][0];
}void solve()
{cin >> n;for(int i = 1; i <= n - 1; i++){int a, b; cin >> a >> b;edges[a].push_back(b);edges[b].push_back(a);}dfs(1, 0);cin >> m;int cur = 1, ans = 0;for(int i = 1; i <= m; i++){int x; cin >> x;ans += dep[x] + dep[cur] - 2 * dep[lca(cur, x)];cur = x;}cout << ans << endl;
}int main()
{cin.tie(0), cout.tie(0), ios::sync_with_stdio(false);int T = 1;// cin >> T;while(T--){solve();}return 0;
}

3. 大量的工作沟通

题目描述：某公司有 N 名员工，编号从 0 至 N−1。其中，除了 0 号员工是老板，其余每名员工都有一个直接领导。我们假设编号为 i 的员工的直接领导是 f__i。

该公司有严格的管理制度，每位员工只能受到本人或直接领导或间接领导的管理。具体来说，规定员工 x 可以管理员工 y，当且仅当 x=y，或 x=f__y，或 x 可以管理 f__y。特别地，0 号员工老板只能自我管理，无法由其他任何员工管理。

现在，有一些同事要开展合作，他们希望找到一位同事来主持这场合作，这位同事必须能够管理参与合作的所有同事。如果有多名满足这一条件的员工，他们希望找到编号最大的员工。你能帮帮他们吗？

【解题】：能够管理给出所有员工的人为所有人的 lca 及其父节点，用 maxn[x] 维护从 x 到根节点的编号最大的员工，输出 max[lca(S)] 即可。

code：

#include <iostream>
#include <vector>
#include <unordered_map>
#include <map>
#include <unordered_set>
#include <set>
#include <algorithm>
#include <cmath>
#include <string>
#include <cstring>
#include <queue>
#include <cstring>using namespace std;
#define endl '\n'
typedef long long LL;
typedef pair<int, int> PII;
#define lc p << 1
#define rc p << 1 | 1
#define lowbit(x) (x & -x)
const int N = 2e5 + 10, M = 25;
const LL MOD = 1e9 + 7;
const double ln2 = log(2);
const double rec_ln2 = 1.0 / ln2;
int n, q;
vector<int> edges[N];
int dep[N], f[N][M];
int maxn[N];void dfs(int x, int fa)
{dep[x] = dep[fa] + 1;f[x][0] = fa;maxn[x] = max(maxn[fa], x);for(int i = 1; i <= 20; i++){f[x][i] = f[f[x][i - 1]][i - 1];}for(auto y : edges[x]){if(y == fa) continue;dfs(y, x);}
}int lca(int x, int y)
{if(dep[x] < dep[y]) swap(x, y);for(int i = 20; i >= 0; i--){if(dep[f[x][i]] >= dep[y]){x = f[x][i];}}if(x == y) return x;for(int i = 20; i >= 0; i--){if(f[x][i] != f[y][i]) {x = f[x][i];y = f[y][i];}}return f[x][0];
}void solve()
{cin >> n;for(int i = 1; i <= n - 1; i++){int x; cin >> x;edges[x].push_back(i);}    dfs(0, 0);cin >> q;while(q--){int m; cin >> m;int cur; cin >> cur;for(int i = 2; i <= m; i++){int x; cin >> x;cur = lca(cur, x);}cout << maxn[cur] << endl;}
}int main()
{cin.tie(0), cout.tie(0), ios::sync_with_stdio(false);int T = 1;// cin >> T;while(T--){solve();}return 0;
}

4. 树上询问

题目描述：给定一棵 n 个点的无根树，有 q 次询问。

每次询问给一个参数三元组 (a,b,c) ，求有多少个 i 满足这棵树在以 i 为根的情况下 a 和 b 的 LCA 为 c 。

【解题】：

a，b 的 lca 为 c，则 c 一定在 a，b 的简单路径上。
若 a，b 的简单路径不包含 c，答案为 0。
否则，会出现以下三种情况.

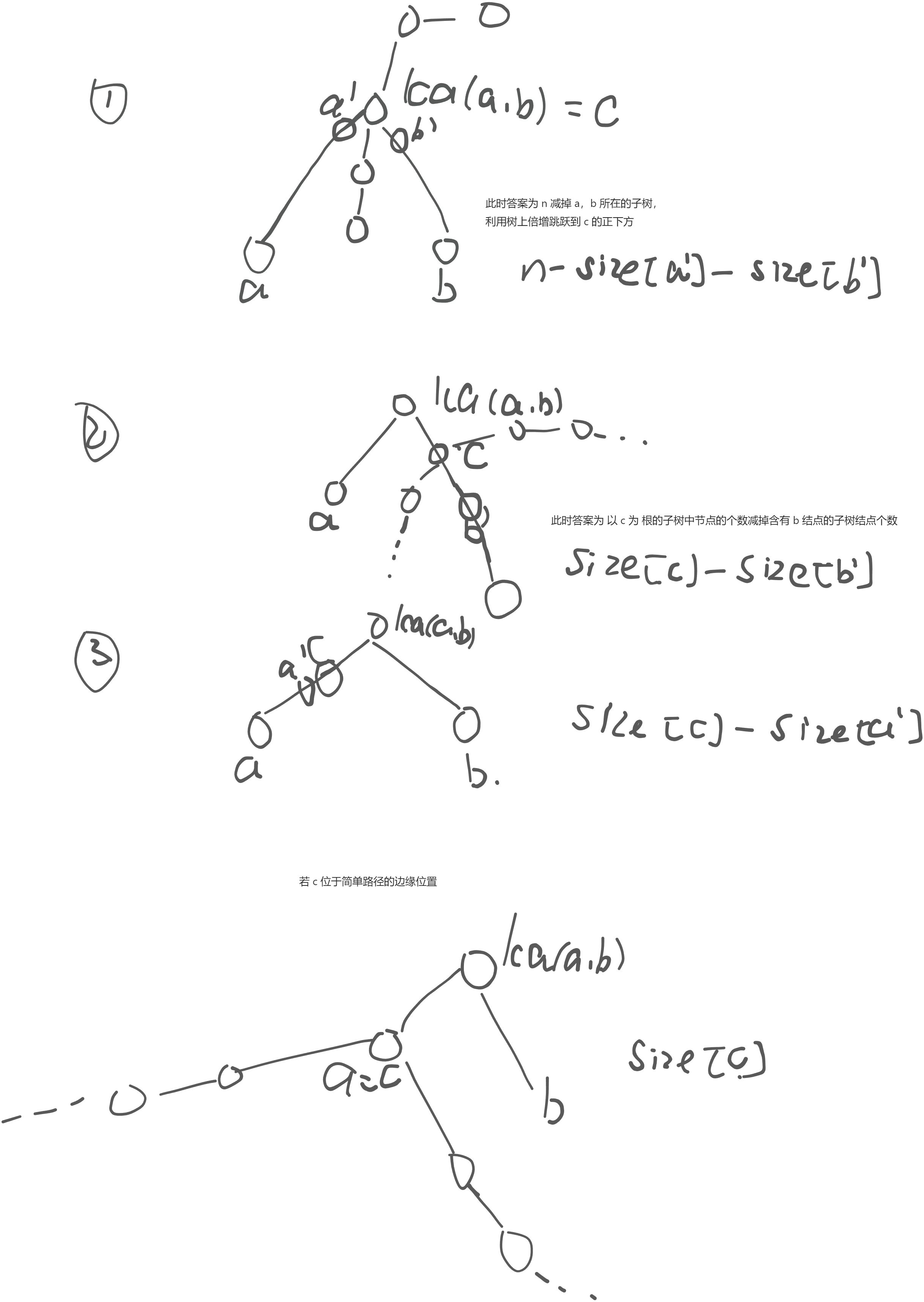
code：

#include <iostream>
#include <vector>
#include <unordered_map>
#include <map>
#include <unordered_set>
#include <set>
#include <algorithm>
#include <cmath>
#include <string>
#include <cstring>
#include <queue>
#include <cstring>using namespace std;
#define endl '\n'
typedef long long LL;
typedef pair<int, int> PII;
#define lc p << 1
#define rc p << 1 | 1
#define lowbit(x) (x & -x)
const int N = 5e5 + 10, M = 25;
const LL MOD = 1e9 + 7;
const double ln2 = log(2);
const double rec_ln2 = 1.0 / ln2;
int dep[N], f[N][M];
int n, q;
vector<int> edges[N];
int cnt[N]; // 以 i 结点为根的子树的大小void dfs(int x, int fa)
{dep[x] = dep[fa] + 1;f[x][0] = fa;for(int i = 1; i <= 20; i++){f[x][i] = f[f[x][i - 1]][i - 1];}cnt[x] = 1;for(auto y : edges[x]){if(y == fa) continue;dfs(y, x);cnt[x] += cnt[y];}
}int lca(int x, int y)
{if(dep[x] < dep[y]) swap(x, y);for(int i = 20; i >= 0; i--){if(dep[f[x][i]] >= dep[y]){x = f[x][i];}}if(x == y) return x;for(int i = 20; i >= 0; i--){if(f[x][i] != f[y][i]){x = f[x][i];y = f[y][i];}}return f[x][0];
}int calc(int x, int y)
{if(x == y) return 0;for(int i = 20; i >= 0; i--){if(dep[f[x][i]] > dep[y]){x = f[x][i];}}return cnt[x];
}void solve()
{cin >> n >> q;for(int i = 1; i <= n - 1; i++){int u, v; cin >> u >> v;edges[u].push_back(v);edges[v].push_back(u);}dfs(1, 0);while(q--){int a, b, c; cin >> a >> b >> c;int x = lca(a, b);if(x == c) cout << n - calc(a, c) - calc(b, c) << endl;else if(lca(a, c) == c && lca(c, x) == x) cout << cnt[c] - calc(a, c) << endl;else if(lca(b, c) == c && lca(c, x) == x) cout << cnt[c] - calc(b, c) << endl;else cout << 0 << endl;}
}int main()
{cin.tie(0), cout.tie(0), ios::sync_with_stdio(false);int T = 1;// cin >> T;while(T--){solve();}return 0;
}

5. 紧急集合 / 聚会

题目大意：欢乐岛上有个非常好玩的游戏，叫做“紧急集合”。在岛上分散有 n 个等待点，有 n−1 条道路连接着它们，每一条道路都连接某两个等待点，且通过这些道路可以走遍所有的等待点，通过道路从一个点到另一个点要花费一个游戏币。

参加游戏的人三人一组，开始的时候，所有人员均任意分散在各个等待点上（每个点同时允许多个人等待），每个人均带有足够多的游戏币（用于支付使用道路的花费）、地图（标明等待点之间道路连接的情况）以及对话机（用于和同组的成员联系）。当集合号吹响后，每组成员之间迅速联系，了解到自己组所有成员所在的等待点后，迅速在 n 个等待点中确定一个集结点，组内所有成员将在该集合点集合，集合所用花费最少的组将是游戏的赢家。

小可可和他的朋友邀请你一起参加这个游戏，由你来选择集合点，聪明的你能够完成这个任务，帮助小可可赢得游戏吗？

【解题】：假设这颗树以 1 为根节点，a，b，c 的位置会出现下面两种情况

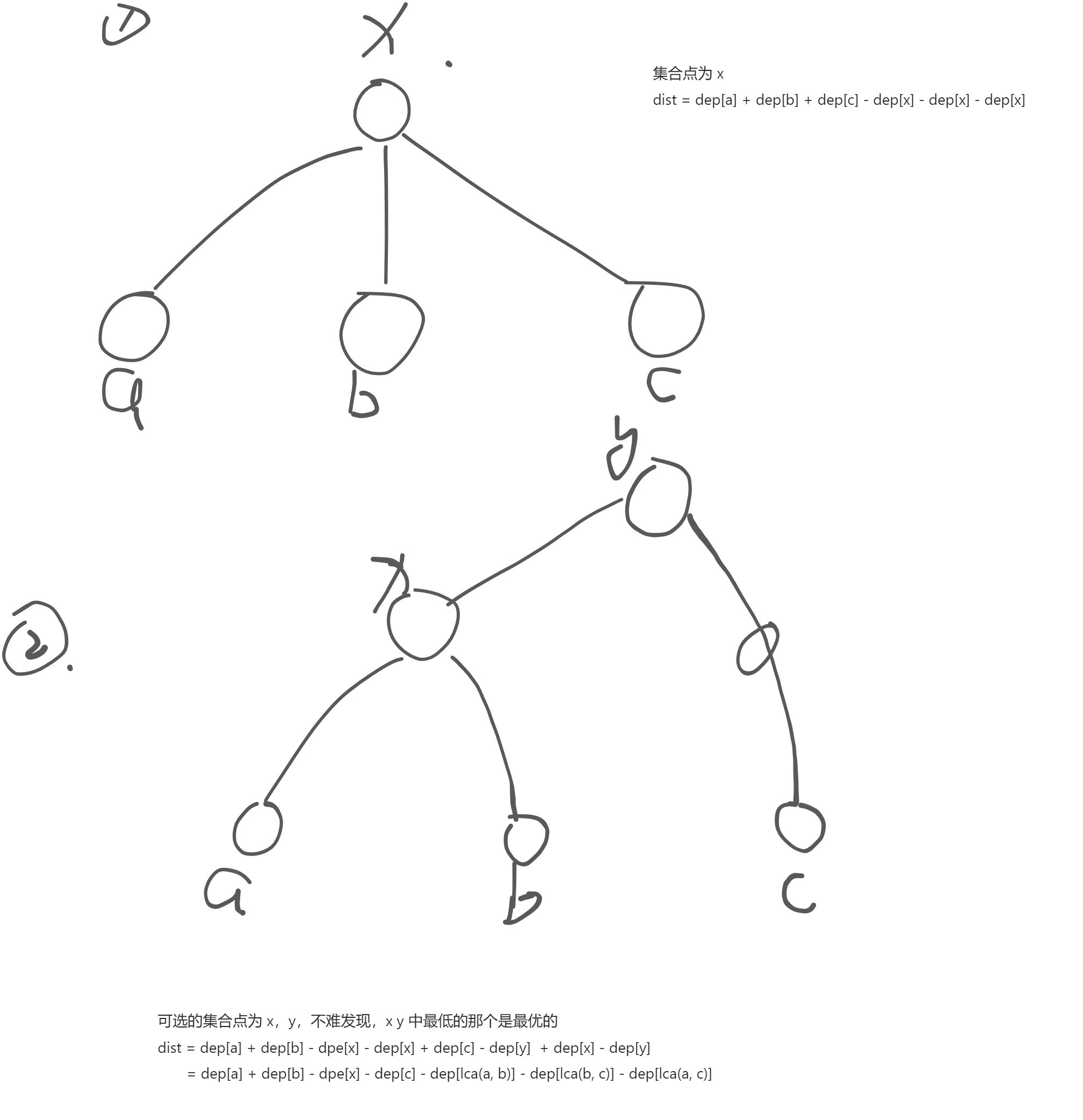
code：

#include <iostream>
#include <vector>
#include <unordered_map>
#include <map>
#include <unordered_set>
#include <set>
#include <algorithm>
#include <cmath>
#include <string>
#include <cstring>
#include <queue>
#include <cstring>using namespace std;
#define endl '\n'
typedef long long LL;
typedef pair<int, int> PII;
#define lc p << 1
#define rc p << 1 | 1
#define lowbit(x) (x & -x)
const int N = 5e5 + 10, M = 25;
const LL MOD = 1e9 + 7;
const double ln2 = log(2);
const double rec_ln2 = 1.0 / ln2;
int n, m;
vector<int> edges[N];
int dep[N], f[N][M];void dfs(int x, int fa)
{dep[x] = dep[fa] + 1;f[x][0] = fa;for(int i = 1; i <= 20; i++)f[x][i] = f[f[x][i - 1]][i - 1];for(auto y : edges[x]){if(y == fa) continue;dfs(y, x);}
}int lca(int x, int y)
{if(dep[x] < dep[y]) swap(x, y);for(int i = 20; i >= 0; i--){if(dep[f[x][i]] >= dep[y]){x = f[x][i];}}if(x == y) return x;for(int i = 20; i >= 0; i--){if(f[x][i] != f[y][i]){x = f[x][i];y = f[y][i];}}return f[x][0];
}void solve()
{cin >> n >> m;for(int i = 1; i <= n - 1; i++){int a, b; cin >> a >> b;edges[a].push_back(b);edges[b].push_back(a);}    dfs(1, 0);while(m--){int x, y, z; cin >> x >> y >> z;int a = lca(x, y), b = lca(y, z), c = lca(x, z);int p = a;if(dep[b] > dep[p]) p = b;if(dep[c] > dep[p]) p = c;cout << p << " " << dep[x] + dep[y] + dep[z] - dep[a] - dep[b] - dep[c] << endl;}
}int main()
{cin.tie(0), cout.tie(0), ios::sync_with_stdio(false);int T = 1;// cin >> T;while(T--){solve();}return 0;
}

6. 仓鼠找 sugar

题目大意：小仓鼠的和他的基（mei）友（zi）sugar 住在地下洞穴中，每个节点的编号为 1∼n。地下洞穴是一个树形结构。这一天小仓鼠打算从从他的卧室（a）到餐厅（b），而他的基友同时要从他的卧室（c）到图书馆（d）。他们都会走最短路径。现在小仓鼠希望知道，有没有可能在某个地方，可以碰到他的基友？

小仓鼠那么弱，还要天天被 zzq 大爷虐，请你快来救救他吧！

【解题】：即a -> b 的简单路径是否会与 c -> d 的简单路径有重合部分。

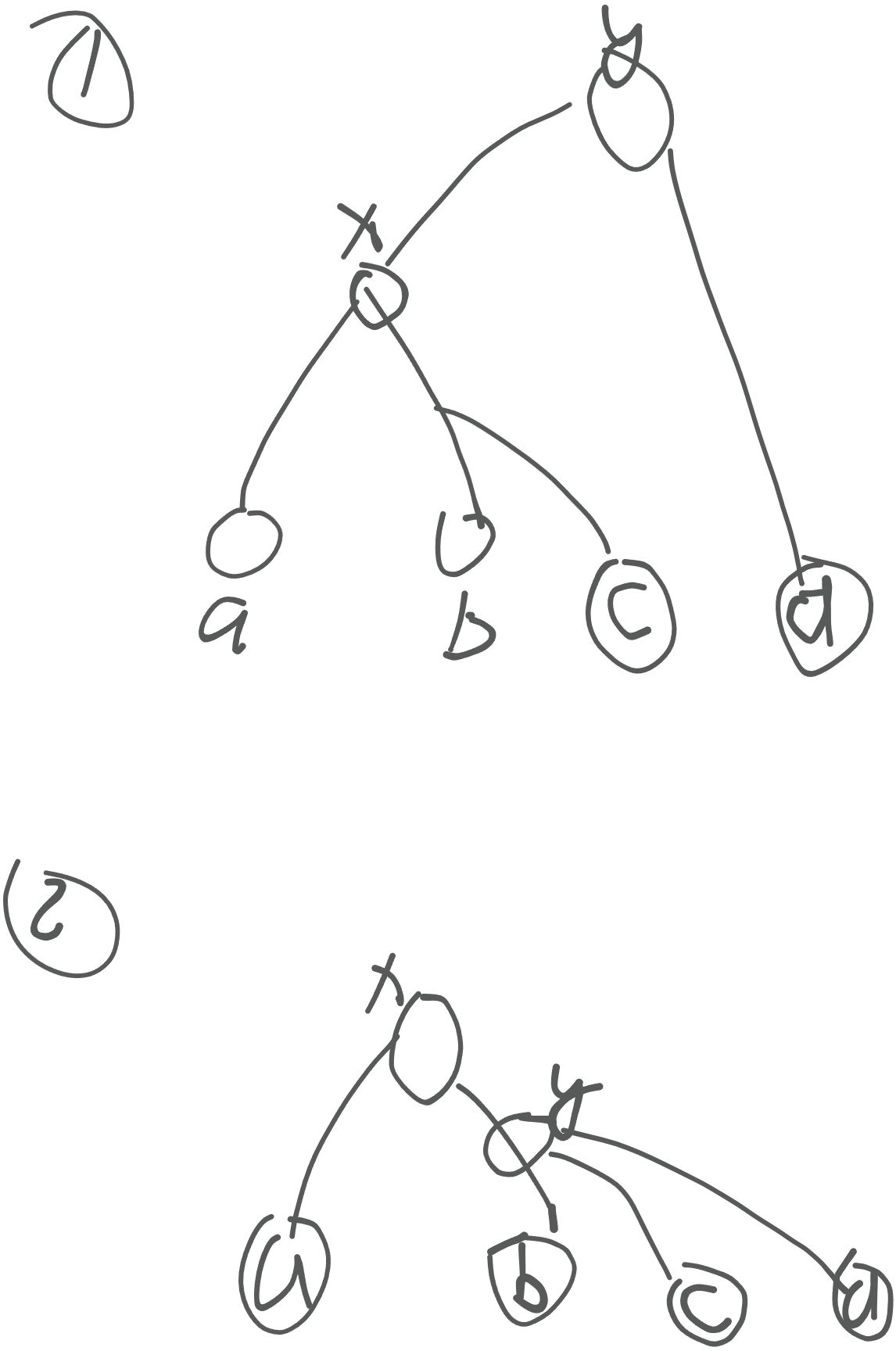
即看 lca(a, b) 是否在 c -> d 的简单路径上，或者 lca(c, d) 是否在 a -> b 。

判断方式也很简单：若 lca(a, b) 在 c -> d 的简单路径上，dist(c, d) = dist(c, x) + dist(d, x)，x 为 lca(a, b)。

code：

#include <iostream>
#include <vector>
#include <unordered_map>
#include <map>
#include <unordered_set>
#include <set>
#include <algorithm>
#include <cmath>
#include <string>
#include <cstring>
#include <queue>
#include <cstring>using namespace std;
#define endl '\n'
typedef long long LL;
typedef pair<int, int> PII;
#define lc p << 1
#define rc p << 1 | 1
#define lowbit(x) (x & -x)
const int N = 1e5 + 10, M = 25;
const LL MOD = 1e9 + 7;
const double ln2 = log(2);
const double rec_ln2 = 1.0 / ln2;
int n, q;
vector<int> edges[N];
int dep[N], f[N][M];void dfs(int x, int fa)
{dep[x] = dep[fa] + 1;f[x][0] = fa;for(int i = 1; i <= 20; i++) f[x][i] = f[f[x][i - 1]][i - 1];for(auto y : edges[x]){if(y == fa) continue; dfs(y, x);}
}int lca(int x, int y)
{if(dep[x] < dep[y]) swap(x, y);for(int i = 20; i >= 0; i--){if(dep[f[x][i]] >= dep[y]){x = f[x][i];}}if(x == y) return x;for(int i = 20; i >= 0; i--){if(f[x][i] != f[y][i]){x = f[x][i];y = f[y][i];}}return f[x][0];
}bool check(int u1, int x, int y, int u2)
{int dist1 = dep[x] + dep[y] - 2 * dep[u2];int a = lca(x, u1), b = lca(y, u1);int dist2 = dep[x] + dep[u1] - 2 * dep[a] + dep[y] + dep[u1] - 2 * dep[b];return dist1 == dist2;
}void solve()
{cin >> n >> q;    for(int i = 1; i <= n - 1; i++){int a, b; cin >> a >> b;edges[a].push_back(b);edges[b].push_back(a);}dfs(1, 0);while(q--){int a, b, c, d; cin >> a >> b >> c >> d;int u1 = lca(a, b), u2 = lca(c, d);if(check(u1, c, d, u2) || check(u2, a, b, u1)) cout << "Y" << endl;else cout << "N" << endl;}
}int main()
{cin.tie(0), cout.tie(0), ios::sync_with_stdio(false);int T = 1;// cin >> T;while(T--){solve();}return 0;
}

7. 货车运输

题目大意：A 国有 n 座城市，编号从 1 到 n，城市之间有 m 条双向道路。每一条道路对车辆都有重量限制，简称限重。

现在有 q 辆货车在运输货物，司机们想知道每辆车在不超过车辆限重的情况下，最多能运多重的货物。

【解题】：贪心 + kruskal重构树 + LCA

对于这种图论问题，显然两地连接的多条边中，只会走最大边权的那一条，因此用kruskal算法重构一颗最大生成树，然后两地的走法显然又是最的越少越好，在一颗树中，两点的最短距离即必须走过的路径即为简单路径，用 LCA 解决，我们要求的是这条最短路径中的最小边权，可以维护一个额外的数组 g[x][i]：表示从 x 向上走 2^i 步后路径中的最小边权。

code：

#include <iostream>
#include <vector>
#include <unordered_map>
#include <map>
#include <unordered_set>
#include <set>
#include <algorithm>
#include <cmath>
#include <string>
#include <cstring>
#include <queue>
#include <cstring>using namespace std;
#define endl '\n'
typedef long long LL;
typedef pair<int, int> PII;
#define lc p << 1
#define rc p << 1 | 1
#define lowbit(x) (x & -x)
const int N = 1e4 + 10, M = 5e4 + 10;
const LL MOD = 1e9 + 7;
const int INF = 0x3f3f3f3f;
const double ln2 = log(2);
const double rec_ln2 = 1.0 / ln2;
int fa[N];
int n, m;
vector<PII> edges[N]; // 存的是重构完的树
struct node
{int x, y, z;bool operator< (const node& b) const{return z > b.z;}
}e[M];
int dep[N], f[N][20], g[N][20];int find(int x)
{return fa[x] == x ? x : fa[x] = find(fa[x]);
}void dfs(int x, int Fa, int w)
{dep[x] = dep[Fa] + 1;f[x][0] = Fa;g[x][0] = w;for(int i = 1; i <= 15; i++) {f[x][i] = f[f[x][i - 1]][i - 1];g[x][i] = min(g[x][i - 1], g[f[x][i - 1]][i - 1]);}for(auto [y, w] : edges[x]){if(y == Fa) continue;dfs(y, x, w);}
}int lca(int x, int y)
{int ret = INF;if(dep[x] < dep[y]) swap(x, y);for(int i = 15; i >= 0; i--){if(dep[f[x][i]] >= dep[y]){ret = min(g[x][i], ret);x = f[x][i];}}if(x == y) return ret;for(int i = 15; i >= 0; i--){if(f[x][i] != f[y][i]){ret = min({ret, g[x][i], g[y][i]});x = f[x][i];y = f[y][i];}}return min({ret, g[x][0], g[y][0]});
}void solve()
{cin >> n >> m;for(int i = 1; i <= n; i++) fa[i] = i;for(int i = 1; i <= m; i++){cin >> e[i].x >> e[i].y >> e[i].z;} sort(e + 1, e + 1 + m);for(int i = 1; i <= m; i++){int x = e[i].x, y = e[i].y, z = e[i].z;int fx = find(x), fy = find(y);if(fx != fy){fa[fx] = fy;edges[x].push_back({y, z});edges[y].push_back({x, z});}}// 可能有多棵树for(int i = 1; i <= n; i++)if(dep[i] == 0)dfs(i, 0, INF); int q; cin >> q;while(q--){int x, y; cin >> x >> y;if(find(x) != find(y)) cout << -1 << endl;else cout << lca(x, y) << endl;}
}int main()
{cin.tie(0), cout.tie(0), ios::sync_with_stdio(false);int T = 1;// cin >> T;while(T--){solve();}return 0;
}

8. 严格次小生成树

题目大意：小 C 最近学了很多最小生成树的算法，Prim 算法、Kruskal 算法、消圈算法等等。正当小 C 洋洋得意之时，小 P 又来泼小 C 冷水了。小 P 说，让小 C 求出一个无向图的次小生成树，而且这个次小生成树还得是严格次小的，也就是说：如果最小生成树选择的边集是 E__M，严格次小生成树选择的边集是 E__S，那么需要满足：(value(e) 表示边 e 的权值) ∑e∈EMvalue(e)<∑e∈ESvalue(e)。

这下小 C 蒙了，他找到了你，希望你帮他解决这个问题。

【解题】：非常好的紫题，使我的大脑旋转。

次小生成树一定是通过替换最小生成树中的一条边的来的。
替换后的生成树的权值为 len + z - x ，其中 len 为最小生成树权值，z 为替换边的权值，x 为 z 连接的两个结点 a，b 的简单路径中的一条边权。
显然 x 越大，结果就更接近次小生成树的权值。
所以要去找 a，b 的简单路径的最大值，通过树上倍增 + dp 寻找。
问题的关键在于如果简单路径上的最大值等于 z，就需要找严格小于 z 的次大边权，因为最小生成树的缘故，这个次大值仅需找一次就可以。
类似于上一题的货车运输维护这一题的 g[x][i]：x 结点往上跳 2^i 步的路径中的最大边权，不过额外要维护 h[x][i]：x 结点往上跳 2^i 步的路径中的严格次大边权，针对于这个 h ，假设一维数轴上分布从小到大分布 x1，x2 表示次大和最大值，当来了一个 x3，如果x3 > x2，次大值为 x2，最大值为 x3；若x3 == x2 不变；若 x3 < x2，最大值不变，次大值为 max(x1, x3)

code：

#include <iostream>
#include <vector>
#include <unordered_map>
#include <map>
#include <unordered_set>
#include <set>
#include <algorithm>
#include <cmath>
#include <string>
#include <cstring>
#include <queue>
#include <cstring>using namespace std;
#define endl '\n'
typedef long long LL;
typedef pair<int, int> PII;
#define lc p << 1
#define rc p << 1 | 1
#define lowbit(x) (x & -x)
const int N = 2e5 + 10, M = 3e5 + 10;
const int INF = 0x3f3f3f3f;
const LL MOD = 1e9 + 7;
const double ln2 = log(2);
const double rec_ln2 = 1.0 / ln2;
int n, m;
vector<PII> edges[N];
int fa[N];
bool st[M];
struct node
{int x, y, z;bool operator<(const node& b) const{return z < b.z;}
}e[M];int dep[N], f[N][25], g[N][25], h[N][25];int find(int x)
{return fa[x] == x ? x : fa[x] = find(fa[x]);
}
// m1 为次大，m2 为最大
void calc(int m3, int& m1, int& m2)
{if(m3 > m2) {m1 = m2;m2 = m3;}else if(m3 < m2) m1 = max(m1, m3);
}void dfs(int x, int dad, int w)
{dep[x] = dep[dad] + 1;f[x][0] = dad;g[x][0] = w;h[x][0] = -INF;for(int i = 1; i <= 20; i++){f[x][i] = f[f[x][i - 1]][i - 1];int m1 = -INF, m2 = -INF;calc(g[x][i - 1], m1, m2);calc(h[x][i - 1], m1, m2);calc(g[f[x][i - 1]][i - 1], m1, m2);calc(h[f[x][i - 1]][i - 1], m1, m2);g[x][i] = m2;h[x][i] = m1;}for(auto& [y, z] : edges[x]){if(y == dad) continue;dfs(y, x, z);}
}void lca(int x, int y, int& m1, int& m2)
{if(dep[x] < dep[y]) swap(x, y);for(int i = 20; i >= 0; i--){if(dep[f[x][i]] >= dep[y]){calc(g[x][i], m1, m2);calc(h[x][i], m1, m2);x = f[x][i];}}if(x == y) return;for(int i = 20; i >= 0; i--){if(f[x][i] != f[y][i]){calc(g[x][i], m1, m2);calc(h[x][i], m1, m2);calc(g[y][i], m1, m2);calc(h[y][i], m1, m2);x = f[x][i];y = f[y][i];}}calc(h[x][0], m1, m2);calc(g[x][0], m1, m2);calc(h[y][0], m1, m2);calc(g[y][0], m1, m2);
}void solve()
{cin >> n >> m;for(int i = 1; i <= n; i++) fa[i] = i;for(int i = 1; i <= m; i++){cin >> e[i].x >> e[i].y >> e[i].z;}sort(e + 1, e + 1 + m);LL len = 0;// kruskal重构最小生成树for(int i = 1; i <= m; i++){int x = e[i].x, y = e[i].y, z = e[i].z;int fx = find(x), fy = find(y);if(fx != fy){len += z;fa[fx] = fy;st[i] = true;edges[x].push_back({y, z});edges[y].push_back({x, z});}}dfs(1, 0, -INF);LL ans = 1e18;for(int i = 1; i <= m; i++){if(st[i]) continue;int x = e[i].x, y = e[i].y, z = e[i].z;int m1 = -INF, m2 = -INF; // m1 为次大，m2 为最大lca(x, y, m1, m2);if(m2 != z) ans = min(len + z - m2, ans);else ans = min(ans, len + z - m1);}cout << ans << endl;
}int main()
{cin.tie(0), cout.tie(0), ios::sync_with_stdio(false);int T = 1;// cin >> T;while(T--){solve();}return 0;
}

二、树链剖分

前言：树链剖分并不是一个简单的部分，这个算法从难度到码量上可以说的上是不太友好，仅仅是预处理部分就需要两个dfs，在加上会与线段树和树上LCA结合，码量通常会将近两百行。不过不要灰心，吃屎的算法不止这一个，要不然ACM也不会这么劝退。

先来介绍以下树链剖分：相比于常规的线性结构，树形结构的区间维护并不方便，针对于这种情况，树链剖分会把树结构剖分成几条链，用一些维护线性结构的数据结构对齐进行维护（线段树，st表，树状数组）。

树链剖分分为 重链剖分，长链剖分 和用于 Link/cut Tree 的剖分（有时被称作「实链剖分」）

（一）、重链剖分

重链剖分可以讲树上的任意一条路径分成不超过 O(logn) 条连续的路径，且路径上的结点的深度各不相同（即是自底向上的一条链，链上所有点的 LCA 为链的一个端点）。

下面通过一道模板题来了解一下流程。

【模板】重链剖分/树链剖分

题目的意思很简单，即完成树上的一些区间操作：

1 x y z，表示将树从 x 到 y 结点最短路径上所有节点的值都加上 z。
2 x y，表示求树从 x 到 y 结点最短路径上所有节点的值之和。
3 x z，表示将以 x 为根节点的子树内所有节点值都加上 z。
4 x，表示求以 x 为根节点的子树内所有节点值之和。

【解题】：

一、重链剖分的过程

（一）、重儿子

一个结点的重儿子指的是该结点得孩子结点中以该节点为根节点得子树中最大得那一个，如果有多个重儿子，任取其一，如果为叶子结点，则无重儿子。

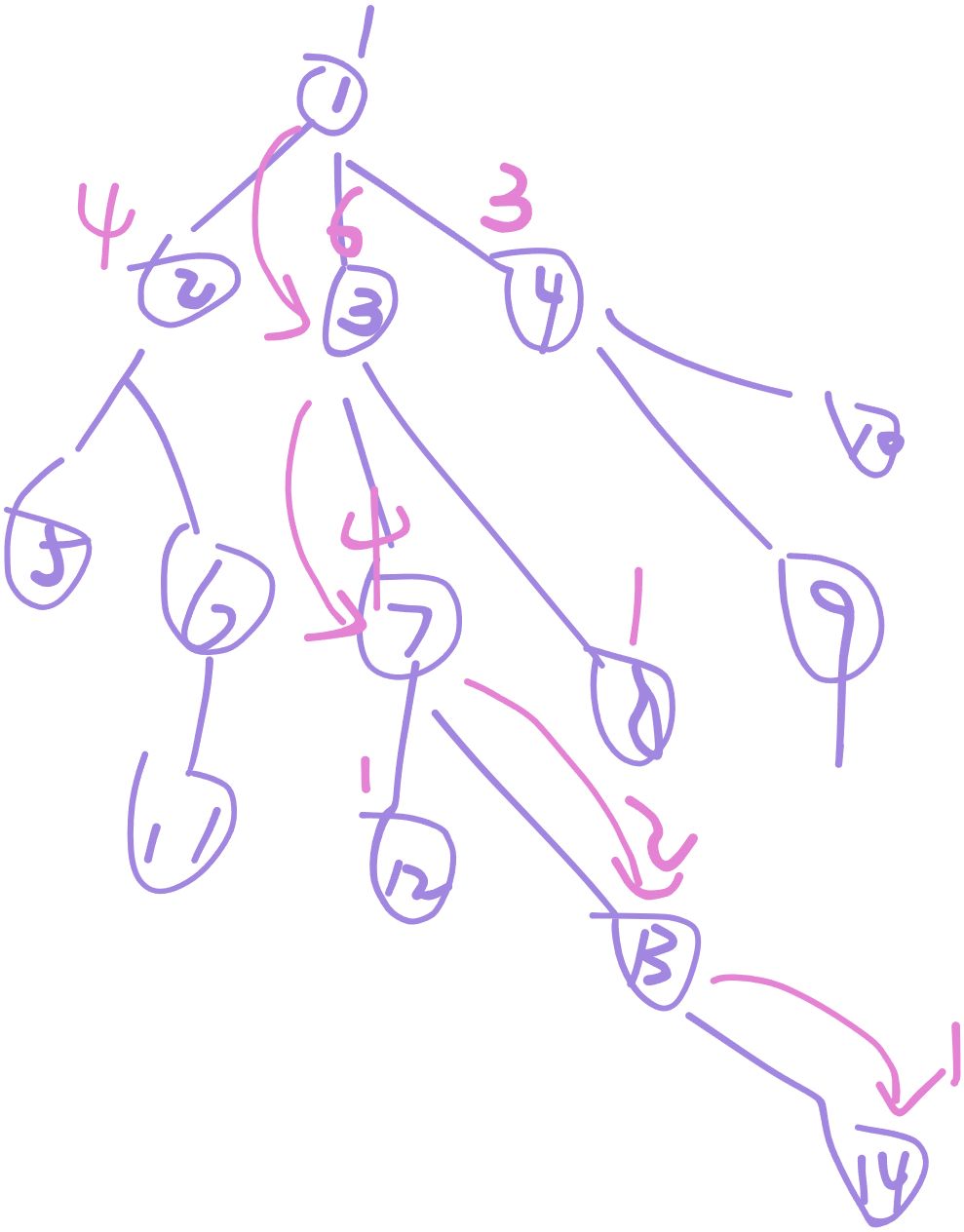
上图中 1 号结点的重儿子为 3 号结点，3 号节点的重儿子为 7 号结点，随后为 13 和 14 号结点。

重链剖分时，优先遍历一个结点重儿子，作为整体重链，当该结点的重链遍历完成之后，遍历其余结点作为一条新开始的重链的头节点。

（二）、dfs1

了解的上面的信息，可以着手书写 dfs1 的代码，在该函数中需要设计下面的几个信息。

- cnt[x]：以 x 结点的根的子树的大小
- fa[x]：x 号结点父节点。
- son[x]：x 号的重儿子。
- dep[x]：x 结点的深度。

void dfs1(int x, int f)
{// x 结点的父节点fa[x] = f; // x 结点的深度dep[x] = dep[f] + 1;cnt[x] = 1;for(auto y : edges[x]){if(y == f) continue;dfs1(y, x);// 树的大小cnt[x] += cnt[y];// 重儿子的设置if(!son[x] || cnt[son[x]] < cnt[y]) son[x] = y;}
}

（三）、dfs2

该 dfs 中需要设置的信息：

dfn[x]：x 结点的遍历序。
top[x]：x 所在重链的头节点。
seg[x]：dfn 需要为 x 的节点的原始编号。

// t 为当前重链的头节点
void dfs2(int x, int t)
{top[x] = t;dfn[x] = ++id;seg[id] = x;if(!son[x]) return; // 叶子节点dfs2(son[x], x, t); // 重儿子优先遍历for(auto y : edges[x]){if(y == fa[x] || y == son[x]) continue; // 其余不是重儿子的结点当作一条新的重链重新开始遍历dfs2(y, x, y);}
}

二、处理区间操作

至此预处理信息已经全部准备完毕，剖分完毕的树中的线性结构如下：

同一个重链的结点，dfn 连续。
同一个子树的结点，dfn 连续。

（一）、线段树的创建

线段树的创建与原始线段树的创建并无太大的区别，唯一的区别在于 node 的左右端点**指向的每个结点的 dfn 序，**所以在初始化 sum 的时候需要找到该 dfn序原始的的结点编号。

void pushup(int p)
{tr[p].sum = (tr[lc].sum + tr[rc].sum) % MOD;
}void build(int p, int l, int r)
{tr[p] = {l, r, 0, 0};if(l >= r){tr[p].sum = a[seg[l]];return;}int mid = (l + r) >> 1;build(lc, l, mid);build(rc, mid + 1, r);pushup(p);
}void lazy(int p, LL k)
{int l = tr[p].l, r = tr[p].r;tr[p].cnt = (tr[p].cnt + k) % MOD;tr[p].sum = (tr[p].sum + (LL)(r - l + 1) * k % MOD);
}void pushdown(int p)
{lazy(lc, tr[p].cnt);lazy(rc, tr[p].cnt);tr[p].cnt = 0;
}void modify(int p, int x, int y, LL k)
{int l = tr[p].l, r = tr[p].r;if(x <= l && y >= r){lazy(p, k);return;}pushdown(p);int mid = (l + r) >> 1;if(x <= mid) modify(lc, x, y, k);if(y >= mid + 1) modify(rc, x, y, k);pushup(p);
}LL query(int p, int x, int y)
{int l = tr[p].l, r = tr[p].r;if(x <= l && y >= r) return tr[p].sum;pushdown(p);int mid = (l + r) >> 1;LL ans = 0;if(x <= mid) ans = (ans + query(lc, x, y)) % MOD;if(y >= mid + 1) ans = (ans + query(rc, x, y)) % MOD;return ans;
}

至此预处理信息已经全部准备完毕，区间修改操作和区间查询操作的本质是一样的，下面以区间修改为例。

（二）、将以 x 为根节点的子树的所有结点统一加上 val。

同一个子树的 dfn 序连续，对于以 x 结点为根结点的子树的 dfn 序为 [dfn[x], dfn[x] + cnt[x] - 1，在用 modify 直接修改就行

void subtr_modify(int x, LL k)
{modify(1, dfn[x], dfn[x] + cnt[x] - 1, k);
}
LL subtr_query(int x)
{return query(1, dfn[x], dfn[x] + cnt[x] - 1);
}

（三）、将 x 到 y 的简单路径上的结点加上 val。

同一条重链的 dfn 序连续。

对于两个可能不在同一条重链中的结点，采用类似 LCA 的跳跃方式，跳跃的高度为直接跳到 top[x]。这个跳跃以 top 较深的结点优先。
x 结点跳跃后，修改这段重链的权值和。
循环进行，知道两个结点处于同一条重链中。
最后修改这两个结点路径的权值。


void path_modify(int x, int y, LL k)
{while(top[x] != top[y]) // 两个结点不位于同一条重链，注意比较的是 dep{if(dep[top[x]] >= dep[top[y]]) // x 结点所在重链的头节点较深{modify(1, dfn[top[x]], dfn[x], k); // 区间修改的是 dfn 序x = fa[top[x]];}else{modify(1, dfn[top[y]], dfn[y], k);y = fa[top[y]];}}// 最后修改这两个已经位于同一条重链的结点modify(1, min(dfn[x], dfn[y]), max(dfn[x], dfn[y]), k);
}LL path_query(int x, int y)
{LL ans = 0;while(top[x] != top[y]){if(dep[top[x]] >= dep[top[y]]) // x 结点所在重链的头节点较深{ans += query(1, dfn[top[x]], dfn[x]);ans %= MOD;x = fa[top[x]];}else{ans += query(1, dfn[top[y]], dfn[y]);ans %= MOD;y = fa[top[y]];}}ans += query(1, min(dfn[x], dfn[y]), max(dfn[x], dfn[y]));ans %= MOD;return ans;
}

（四）、完整 code

#include <iostream>
#include <vector>
#include <unordered_map>
#include <map>
#include <unordered_set>
#include <set>
#include <algorithm>
#include <cmath>
#include <string>
#include <cstring>
#include <queue>
#include <cstring>using namespace std;
#define endl '\n'
typedef long long LL;
typedef pair<int, int> PII;
#define lc p << 1
#define rc p << 1 | 1
#define lowbit(x) (x & -x)
const int N = 1e5 + 10;
const double ln2 = log(2);
const double rec_ln2 = 1.0 / ln2;
vector<int> edges[N];
int n, m, r;
LL MOD;
int dep[N], cnt[N], son[N], fa[N];
int top[N], seg[N], dfn[N], id;
LL a[N]; // 存储节点的权值
struct node
{int l, r;LL sum;LL cnt; // 懒标记
}tr[N << 2];void dfs1(int x, int f)
{// x 结点的父节点fa[x] = f; // x 结点的深度dep[x] = dep[f] + 1;cnt[x] = 1;for(auto y : edges[x]){if(y == f) continue;dfs1(y, x);// 树的大小cnt[x] += cnt[y];// 重儿子的设置if(!son[x] || cnt[son[x]] < cnt[y]) son[x] = y;}
}
// t 为当前重链的头节点
void dfs2(int x, int t)
{top[x] = t;dfn[x] = ++id;seg[id] = x;if(!son[x]) return; // 叶子节点dfs2(son[x], t); // 重儿子优先遍历for(auto y : edges[x]){if(y == fa[x] || y == son[x]) continue; // 其余不是重儿子的结点当作一条新的重链重新开始遍历dfs2(y, y);}
}void pushup(int p)
{tr[p].sum = (tr[lc].sum + tr[rc].sum) % MOD;
}void build(int p, int l, int r)
{tr[p] = {l, r, 0, 0};if(l >= r){tr[p].sum = a[seg[l]] % MOD; // 虽然输入都是 int 范围内的数，但是很无语的一点是，还是有爆的风险，尽量取模吧return;}int mid = (l + r) >> 1;build(lc, l, mid);build(rc, mid + 1, r);pushup(p);
}void lazy(int p, LL k)
{int l = tr[p].l, r = tr[p].r;tr[p].cnt = (tr[p].cnt + k) % MOD;tr[p].sum = (tr[p].sum + (LL)(r - l + 1) * k % MOD) % MOD;
}void pushdown(int p)
{lazy(lc, tr[p].cnt);lazy(rc, tr[p].cnt);tr[p].cnt = 0;
}void modify(int p, int x, int y, LL k)
{int l = tr[p].l, r = tr[p].r;if(x <= l && y >= r){lazy(p, k);return;}pushdown(p);int mid = (l + r) >> 1;if(x <= mid) modify(lc, x, y, k);if(y >= mid + 1) modify(rc, x, y, k);pushup(p);
}LL query(int p, int x, int y)
{int l = tr[p].l, r = tr[p].r;if(x <= l && y >= r) return tr[p].sum;pushdown(p);int mid = (l + r) >> 1;LL ans = 0;if(x <= mid) ans = (ans + query(lc, x, y)) % MOD;if(y >= mid + 1) ans = (ans + query(rc, x, y)) % MOD;return ans;
}void subtr_modify(int x, LL k)
{modify(1, dfn[x], dfn[x] + cnt[x] - 1, k);
}
LL subtr_query(int x)
{return query(1, dfn[x], dfn[x] + cnt[x] - 1);
}
void path_modify(int x, int y, LL k)
{while(top[x] != top[y]) // 两个结点不位于同一条重链，注意比较的是 dep{if(dep[top[x]] >= dep[top[y]]) // x 结点所在重链的头节点较深{modify(1, dfn[top[x]], dfn[x], k); // 区间修改的是 dfn 序x = fa[top[x]];}else{modify(1, dfn[top[y]], dfn[y], k);y = fa[top[y]];}}// 最后修改这两个已经位于同一条重链的结点modify(1, min(dfn[x], dfn[y]), max(dfn[x], dfn[y]), k);
}LL path_query(int x, int y)
{LL ans = 0;while(top[x] != top[y]){if(dep[top[x]] >= dep[top[y]]) // x 结点所在重链的头节点较深{ans += query(1, dfn[top[x]], dfn[x]);ans %= MOD;x = fa[top[x]];}else{ans += query(1, dfn[top[y]], dfn[y]);ans %= MOD;y = fa[top[y]];}}ans += query(1, min(dfn[x], dfn[y]), max(dfn[x], dfn[y]));ans %= MOD;return ans;
}void solve()
{cin >> n >> m >> r >> MOD;for(int i = 1; i <= n; i++) cin >> a[i];for(int i = 1; i <= n - 1; i++) {int u, v; cin >> u >> v;edges[u].push_back(v);edges[v].push_back(u);}dfs1(r, 0);dfs2(r, r);build(1, 1, n);int op, x, y;LL z;while(m--){cin >> op;if(op == 1){cin >> x >> y >> z;z %= MOD;path_modify(x, y, z);}else if(op == 2){cin >> x >> y;cout << path_query(x, y) << endl;}else if(op == 3){cin >> x >> z;z %= MOD;subtr_modify(x, z);}else {cin >> x;cout << subtr_query(x) << endl;;}}
}int main()
{cin.tie(0), cout.tie(0), ios::sync_with_stdio(false);int T = 1;// cin >> T;while(T--){solve();}return 0;
}

2. 树链剖分解决LCA

通过上面模板的学习，我们了解到了重链中的跳跃，这种跳跃还可以解决 LCA 问题，即两个不同重链的结点跳跃到同时一个重链中，返回较低或者 dfn 较小的那一个。

#include <iostream>
#include <vector>
#include <unordered_map>
#include <map>
#include <unordered_set>
#include <set>
#include <algorithm>
#include <cmath>
#include <string>
#include <cstring>
#include <queue>
#include <cstring>using namespace std;
#define endl '\n'
typedef long long LL;
typedef pair<int, int> PII;
#define lc p << 1
#define rc p << 1 | 1
#define lowbit(x) (x & -x)
const int N = 5e5 + 10;
const LL MOD = 1e9 + 7;
const double ln2 = log(2);
const double rec_ln2 = 1.0 / ln2;
int dep[N], fa[N], son[N], cnt[N];
int top[N], dfn[N], id; // 无需建立线段树，seg 不需要了
vector<int> edges[N];
int n, m, s;void dfs1(int x, int f)
{dep[x] = dep[f] + 1;cnt[x] = 1;fa[x] = f;for(auto y : edges[x]){if(y == f) continue;dfs1(y, x);cnt[x] += cnt[y];if(!son[x] || cnt[son[x]] < cnt[y]) son[x] = y;}
}void dfs2(int x, int t)
{dfn[x] = ++id;top[x] = t;if(!son[x]) return;dfs2(son[x], t);for(auto y : edges[x]){if(y == fa[x] || y == son[x]) continue;dfs2(y, y);}
}int lca(int x, int y)
{while(top[x] != top[y]){if(dep[top[x]] >= dep[top[y]]){x = fa[top[x]];}else{y = fa[top[y]];}}return (dfn[x] <= dfn[y] ? x : y);
}void solve()
{cin >> n >> m >> s;for(int i = 1; i < n; i++){int x, y; cin >> x >> y;edges[x].push_back(y);edges[y].push_back(x);}dfs1(s, 0);dfs2(s, s);while(m--){int a, b; cin >> a >> b;cout << lca(a, b) << endl;}
}int main()
{cin.tie(0), cout.tie(0), ios::sync_with_stdio(false);int T = 1;// cin >> T;while(T--){solve();}return 0;
}

3. 练习题

一、P2590 [ZJOI2008] 树的统计

题目描述：

I. CHANGE u t : 把结点 u 的权值改为 t。
II. QMAX u v: 询问从点 u 到点 v 的路径上的节点的最大权值。
III. QSUM u v: 询问从点 u 到点 v 的路径上的节点的权值和。

注意：从点 u 到点 v 的路径上的节点包括 u 和 v 本身。
【解题】：对树的单点修改 + 区间查询。树链剖分 + 线段树。

code：

#include <iostream>
#include <vector>
#include <unordered_map>
#include <map>
#include <unordered_set>
#include <set>
#include <algorithm>
#include <cmath>
#include <string>
#include <cstring>
#include <queue>
#include <cstring>using namespace std;
#define endl '\n'
typedef long long LL;
typedef pair<int, int> PII;
#define lc p << 1
#define rc p << 1 | 1
#define lowbit(x) (x & -x)
const int N = 3e4 + 10;
const LL MOD = 1e9 + 7;
const double ln2 = log(2);
const double rec_ln2 = 1.0 / ln2;
int dep[N], fa[N], cnt[N], son[N];
int dfn[N], seg[N], top[N], id;
LL a[N];
struct node
{int l, r;LL sum, max;
}tr[N << 2];
vector<int> edges[N];
int n;void dfs1(int x, int f)
{dep[x] = dep[f] + 1;cnt[x] = 1;fa[x] = f;for(auto y : edges[x]){if(y == f) continue;dfs1(y, x);cnt[x] += cnt[y];if(!son[x] || cnt[son[x]] < cnt[y]) son[x] = y;}
}void dfs2(int x, int t)
{top[x] = t;dfn[x] = ++id; seg[id] = x;if(!son[x]) return;dfs2(son[x], t);for(auto y : edges[x]){if(y == fa[x] || y == son[x]) continue;dfs2(y, y);}
}void pushup(int p)
{tr[p].max = max(tr[lc].max, tr[rc].max);tr[p].sum = tr[lc].sum + tr[rc].sum;
}void build(int p, int l, int r)
{tr[p] = {l, r, 0, 0};if(l >= r){tr[p].max = tr[p].sum = a[seg[l]];return;}int mid = (l + r) >> 1;build(lc, l, mid);build(rc, mid + 1, r);pushup(p);
}void modify(int p, int x, LL k)
{int l = tr[p].l, r = tr[p].r;if(l == r && l == x){tr[p].sum = tr[p].max = k;return;}int mid = (l + r) >> 1;if(x <= mid) modify(lc, x, k);else modify(rc, x, k);pushup(p);
}LL query_sum(int p, int x, int y)
{int l = tr[p].l, r = tr[p].r;if(x <= l && y >= r) return tr[p].sum;int mid = (l + r) >> 1;LL ans = 0;if(x <= mid) ans += query_sum(lc, x, y);if(y >= mid + 1) ans += query_sum(rc, x, y);return ans;
}LL query_max(int p, int x, int y)
{int l = tr[p].l, r = tr[p].r;if(x <= l && y >= r) return tr[p].max;int mid = (l + r) >> 1;LL ans = -1e18;if(x <= mid) ans = max(ans, query_max(lc, x, y));if(y >= mid + 1) ans = max(ans, query_max(rc, x, y));return ans;
}LL path_max(int x, int y)
{LL ans = -1e18;while(top[x] != top[y]){if(dep[top[x]] >= dep[top[y]]){ans = max(ans, query_max(1, dfn[top[x]], dfn[x]));x = fa[top[x]];}else{ans = max(ans, query_max(1, dfn[top[y]], dfn[y]));y = fa[top[y]];}}return max(ans, query_max(1, min(dfn[x], dfn[y]), max(dfn[x], dfn[y])));
}LL path_sum(int x, int y)
{LL ans = 0;while(top[x] != top[y]){if(dep[top[x]] >= dep[top[y]]){ans += query_sum(1, dfn[top[x]], dfn[x]);x = fa[top[x]];}else{ans += query_sum(1, dfn[top[y]], dfn[y]);y = fa[top[y]];}}return ans + query_sum(1, min(dfn[x], dfn[y]), max(dfn[x], dfn[y]));
}void solve()
{cin >> n;for(int i = 1; i <= n - 1; i++){int x, y; cin >> x >> y;edges[x].push_back(y);edges[y].push_back(x);}for(int i = 1; i <= n; i++) cin >> a[i];// 题目中给的是无根树，但是简单路径和根节点无关dfs1(1, 0);dfs2(1, 1); build(1, 1, n);int q; cin >> q;string op; int x, y;while(q--){cin >> op >> x >> y;if(op == "QMAX"){cout << path_max(x, y) << endl;}else if(op == "QSUM"){cout << path_sum(x, y) << endl;}else{modify(1, dfn[x], y);}}
}int main()
{cin.tie(0), cout.tie(0), ios::sync_with_stdio(false);int T = 1;// cin >> T;while(T--){solve();}return 0;
}

二、 P2146 [NOI2015] 软件包管理器

题目描述：你决定设计你自己的软件包管理器。不可避免地，你要解决软件包之间的依赖问题。如果软件包 a 依赖软件包 b，那么安装软件包 a 以前，必须先安装软件包 b。同时，如果想要卸载软件包 b，则必须卸载软件包 a。

现在你已经获得了所有的软件包之间的依赖关系。而且，由于你之前的工作，除 0 号软件包以外，在你的管理器当中的软件包都会依赖一个且仅一个软件包，而 0 号软件包不依赖任何一个软件包。且依赖关系不存在环（即不会存在 m 个软件包 a1,a2,…,a__m，对于 i<m，a__i 依赖 a__i+1，而 a__m 依赖 a1 的情况）。

现在你要为你的软件包管理器写一个依赖解决程序。根据反馈，用户希望在安装和卸载某个软件包时，快速地知道这个操作实际上会改变多少个软件包的安装状态（即安装操作会安装多少个未安装的软件包，或卸载操作会卸载多少个已安装的软件包），你的任务就是实现这个部分。

注意，安装一个已安装的软件包，或卸载一个未安装的软件包，都不会改变任何软件包的安装状态，即在此情况下，改变安装状态的软件包数为 0。

【解题】：题目中说的很麻烦，但是题还是很简单的。

install 把 x 结点到 1 结点的所有状态变为 1 （已安装）。
uninstall 把以 x 结点为根的子树的所有节点的状态变为 0 （未安装）

code：

#include <iostream>
#include <vector>
#include <unordered_map>
#include <map>
#include <unordered_set>
#include <set>
#include <algorithm>
#include <cmath>
#include <string>
#include <cstring>
#include <queue>
#include <cstring>using namespace std;
#define endl '\n'
typedef long long LL;
typedef pair<int, int> PII;
#define lc p << 1
#define rc p << 1 | 1
#define lowbit(x) (x & -x)
const int N = 1e5 + 10;
const LL MOD = 1e9 + 7;
const double ln2 = log(2);
const double rec_ln2 = 1.0 / ln2;
int dep[N], fa[N], cnt[N], son[N];
int dfn[N], seg[N], top[N], id;
LL a[N];
struct node
{int l, r;LL sum; // 1 的个数int chage; // -1 为无效状态，0 1 记录懒标记
}tr[N << 2];
vector<int> edges[N];
int n;void dfs1(int x, int f)
{dep[x] = dep[f] + 1;cnt[x] = 1;fa[x] = f;for(auto y : edges[x]){if(y == f) continue;dfs1(y, x);cnt[x] += cnt[y];if(!son[x] || cnt[son[x]] < cnt[y]) son[x] = y;}
}void dfs2(int x, int t)
{top[x] = t;dfn[x] = ++id; seg[id] = x;if(!son[x]) return;dfs2(son[x], t);for(auto y : edges[x]){if(y == fa[x] || y == son[x]) continue;dfs2(y, y);}
}void pushup(int p)
{tr[p].sum = tr[lc].sum + tr[rc].sum;
}void build(int p, int l, int r)
{tr[p] = {l, r, 0, -1};if(l >= r) return;int mid = (l + r) >> 1;build(lc, l, mid);build(rc, mid + 1, r);pushup(p);
}void lazy(int p, int k)
{if(k == -1) return;tr[p].chage = k;tr[p].sum = (tr[p].r - tr[p].l + 1) * k;
}void pushdown(int p)
{lazy(lc, tr[p].chage);lazy(rc, tr[p].chage);tr[p].chage = -1;
}void modify(int p, int x, int y, int k)
{int l = tr[p].l, r = tr[p].r;if(x <= l && y >= r){lazy(p, k);return;}pushdown(p);int mid = (l + r) >> 1;if(x <= mid) modify(lc, x, y, k);if(y >= mid + 1) modify(rc, x, y, k);pushup(p);
}int query(int p, int x, int y)
{int l = tr[p].l, r = tr[p].r;if(x <= l && y >= r) return tr[p].sum;pushdown(p);int mid = (l + r) >> 1;int ans = 0;if(x <= mid) ans += query(lc, x, y);if(y >= mid + 1) ans += query(rc, x, y);return ans;
}int install(int x)
{int y = 1;int tmp = x;int ans = query(1, dfn[y], dfn[x]);while(top[x] != top[y]){if(dep[top[x]] >= dep[top[1]]){modify(1, dfn[top[x]], dfn[x], 1);x = fa[top[x]];}else{modify(1, dfn[top[y]], dfn[y], 1);y = fa[top[y]];}}modify(1, min(dfn[x], dfn[y]), max(dfn[x], dfn[y]), 1);return abs(ans - query(1, dfn[y], dfn[tmp]));
}int uninstall(int x)
{int ans = query(1, dfn[x], dfn[x] + cnt[x] - 1);modify(1, dfn[x], dfn[x] + cnt[x] - 1, 0);return ans;
}void solve()
{cin >> n;for(int i = 2; i <= n; i++){int x; cin >> x;x++;edges[x].push_back(i);edges[i].push_back(x);}   dfs1(1, 0);dfs2(1, 1);build(1, 1, n);int q; cin >> q;string op; int x;while(q--){cin >> op >> x; x++;if(op == "install"){cout << install(x) << endl;}else{cout << uninstall(x) << endl;}}
}int main()
{cin.tie(0), cout.tie(0), ios::sync_with_stdio(false);int T = 1;// cin >> T;while(T--){solve();}return 0;
}

三、P2486 [SDOI2011] 染色

题目大意：
给定一棵 n 个节点的无根树，共有 m 个操作，操作分为两种：

将节点 a 到节点 b 的路径上的所有点（包括 a 和 b）都染成颜色 c。
询问节点 a 到节点 b 的路径上的颜色段数量。

颜色段的定义是极长的连续相同颜色被认为是一段。例如 112221 由三段组成：11、222、1。

【解题】：树链剖分 + 线段树 + 分治。

可以说这一题是很板的。假设本来就是对区间的操作，这和线段树的例题里面的有多少连续的 1 的思路还是很像的。这一题无非就是树上操作，树链剖分以下就行，比较麻烦的是统计结果的时候需要注意什么情况减一。

#include <iostream>
#include <vector>
#include <unordered_map>
#include <map>
#include <unordered_set>
#include <set>
#include <algorithm>
#include <cmath>
#include <string>
#include <cstring>
#include <queue>
#include <cstring>using namespace std;
#define endl '\n'
typedef long long LL;
typedef pair<int, int> PII;
#define lc p << 1
#define rc p << 1 | 1
#define lowbit(x) (x & -x)
const int N = 2e5 + 10;
const LL MOD = 1e9 + 7;
const double ln2 = log(2);
const double rec_ln2 = 1.0 / ln2;
int dep[N], cnt[N], son[N], fa[N];
int seg[N], dfn[N], top[N], id;
int n, q, a[N];
vector<int> edges[N];
struct node
{int l, r;int lcolor, rcolor;int sum;int change; // 懒标记，0 表示无有效信息
}tr[N << 2];void dfs1(int x, int f)
{dep[x] = dep[f] + 1;cnt[x] = 1;fa[x] = f;for(auto y : edges[x]){if(y == f) continue;dfs1(y, x);cnt[x] += cnt[y];if(!son[x] || cnt[son[x]] < cnt[y]) son[x] = y;}
}void dfs2(int x, int t)
{top[x] = t;dfn[x] = ++id;seg[id] = x;if(!son[x]) return;dfs2(son[x], t);for(auto y : edges[x]){if(y == fa[x] || y == son[x]) continue;dfs2(y, y);}
}void pushup(node& C, node& L, node& R)
{C.lcolor = L.lcolor;C.rcolor = R.rcolor;C.sum = L.sum + R.sum - (L.rcolor == R.lcolor);
}void build(int p, int l, int r)
{tr[p] = {l, r, 0, 0, 0, 0};if(l >= r){tr[p].lcolor = tr[p].rcolor = a[seg[l]];tr[p].sum = 1;return;}int mid = (l + r) >> 1;build(lc, l, mid);build(rc, mid + 1, r);pushup(tr[p], tr[lc], tr[rc]);
}void lazy(int p, int k)
{if(k == 0) return;tr[p].lcolor = tr[p].rcolor = k;tr[p].sum = 1;tr[p].change = k;
}void pushdown(int p)
{lazy(lc, tr[p].change);lazy(rc, tr[p].change);tr[p].change = 0;
}void modify(int p, int x, int y, int k)
{int l = tr[p].l, r = tr[p].r;if(x <= l && y >= r){lazy(p, k);return;}pushdown(p);int mid = (l + r) >> 1;if(x <= mid) modify(lc, x, y, k);if(y >= mid + 1) modify(rc, x, y, k);pushup(tr[p], tr[lc], tr[rc]);
}node query(int p, int x, int y)
{int l = tr[p].l, r = tr[p].r;if(x <= l && y >= r) return tr[p];pushdown(p);int mid = (l + r) >> 1;if(y <= mid) return query(lc, x, y);if(x >= mid + 1) return query(rc, x, y);else{node C, L = query(lc, x, y), R = query(rc, x, y);pushup(C, L, R);return C;}
}void path_modify(int x, int y, int k)
{while(top[x] != top[y]){if(dep[top[x]] >= dep[top[y]]){modify(1, dfn[top[x]], dfn[x], k);x = fa[top[x]];}else{modify(1, dfn[top[y]], dfn[y], k);y = fa[top[y]];}}modify(1, min(dfn[x], dfn[y]), max(dfn[x], dfn[y]), k);
}int path_query(int x, int y)
{int ans = 0, sonc, fac; // 重链交接部分的头和其孩子while(top[x] != top[y]){if(dep[top[x]] >= dep[top[y]]){ans += query(1, dfn[top[x]], dfn[x]).sum;sonc = query(1, dfn[top[x]], dfn[top[x]]).lcolor;fac = query(1, dfn[fa[top[x]]], dfn[fa[top[x]]]).lcolor;x = fa[top[x]];}else{ans += query(1, dfn[top[y]], dfn[y]).sum;sonc = query(1, dfn[top[y]], dfn[top[y]]).lcolor;fac = query(1, dfn[fa[top[y]]], dfn[fa[top[y]]]).lcolor;y = fa[top[y]];}if(sonc == fac) ans--;}ans += query(1, min(dfn[x], dfn[y]), max(dfn[x], dfn[y])).sum;return ans;
}void solve()
{cin >> n >> q;for(int i = 1; i <= n; i++) cin >> a[i];for(int i = 1; i <= n - 1; i++){int x, y; cin >> x >> y;edges[x].push_back(y);edges[y].push_back(x);}// 虽说是无根树，但是还是仅涉及到简单路径的信息，无关根节点dfs1(1, 0);dfs2(1, 1);build(1, 1, n);char op; int a, b, c;while(q--){cin >> op;if(op == 'C'){cin >> a >> b >> c;path_modify(a, b, c);}else{cin >> a >> b;cout << path_query(a, b) << endl;}}
}int main()
{cin.tie(0), cout.tie(0), ios::sync_with_stdio(false);int T = 1;// cin >> T;while(T--){solve();}return 0;
}