【从零开始的大模型原理与实践教程】--第五章:动手搭建大模型LLaMA2

Meta（原Facebook）于2023年2月发布第一款基于Transformer结构的大型语言模型LLaMA，并于同年7月发布同系列模型LLaMA2。我们在第四章已经学习和了解了LLM，以及如何训练LLM等内容。本小节我们就来学习如何动手实现一个LLaMA2模型。

LLaMA2 模型结构如下图5.1所示：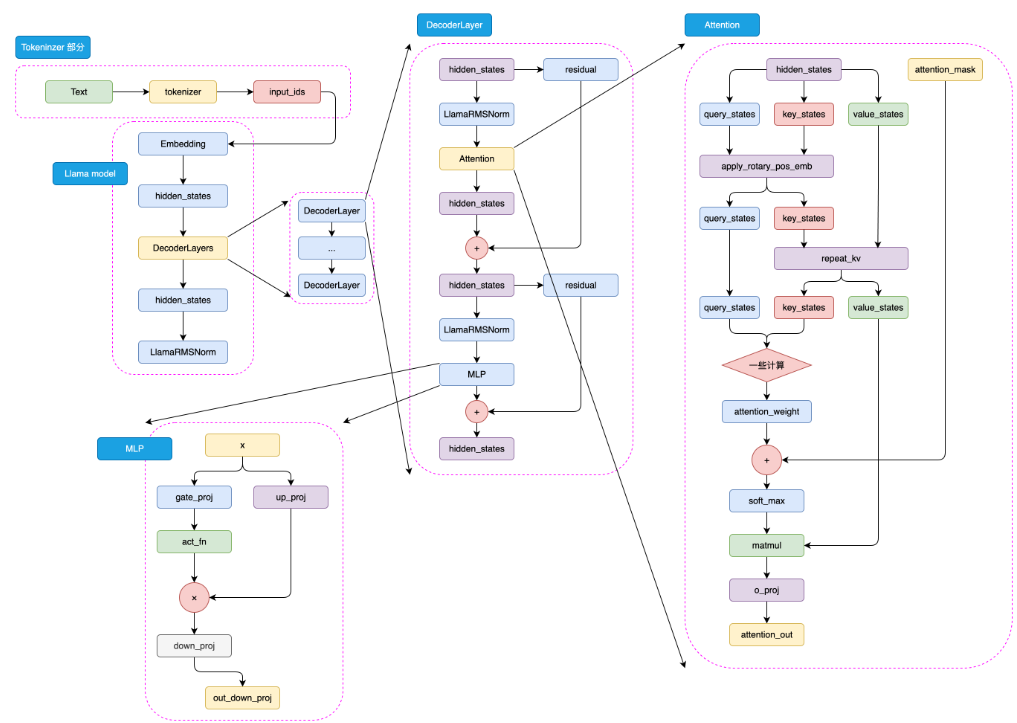

目录

1.动手实现一个 LLaMA2 大模型

1.1.定义超参数

1.2.构建 RMSNorm

1.3.构建 LLaMA2 Attention

1.3.1.repeat_kv

1.3.2.旋转嵌入

1.3.3.组装LLaMA2 Attention

1.4.构建 LLaMA2 MLP模块

1.5.LLaMA2 Decoder Layer

1.6.构建 LLaMA2 模型

2.训练 Tokenizer

2.1.Word-based Tokenizer

2.2.Character-based Tokenizer

2.3.训练一个 Tokenizer

Step 1: 安装和导入依赖库

Step 2: 加载训练数据

Step 3: 创建配置文件

Step 4: 训练 BPE Tokenizer

Step 5: 使用训练好的 Tokenizer

3.预训练一个小型LLM

3.1.数据下载

3.2 训练 Tokenizer

3.3.Dataset

3.4.预训练

3.5.SFT 训练

3.6 使用模型生成文本

参考资料

---

1.动手实现一个 LLaMA2 大模型

1.1.定义超参数

首先我们需要定义一些超参数，这些超参数包括模型的大小、层数、头数、词嵌入维度、隐藏层维度等等。这些超参数可以根据实际情况进行调整。

这里我们自定义一个ModelConfig类，来存储和记录我们的超参数，这里我们继承了PretrainedConfig类，这是transformers库中的参数类，我们可以通过继承这个类来方便的使用transformers库中的一些功能，也方便在后续导出Hugging Face模型。

from transformers import PretrainedConfigclass ModelConfig(PretrainedConfig):model_type = "Tiny-K"def __init__(self,dim: int = 768, # 模型维度n_layers: int = 12, # Transformer的层数n_heads: int = 16, # 注意力机制的头数n_kv_heads: int = 8, # 键值头的数量vocab_size: int = 6144, # 词汇表大小hidden_dim: int = None, # 隐藏层维度multiple_of: int = 64, norm_eps: float = 1e-5, # 归一化层的epsmax_seq_len: int = 512, # 最大序列长度dropout: float = 0.0, # dropout概率flash_attn: bool = True, # 是否使用Flash Attention**kwargs,):self.dim = dimself.n_layers = n_layersself.n_heads = n_headsself.n_kv_heads = n_kv_headsself.vocab_size = vocab_sizeself.hidden_dim = hidden_dimself.multiple_of = multiple_ofself.norm_eps = norm_epsself.max_seq_len = max_seq_lenself.dropout = dropoutself.flash_attn = flash_attnsuper().__init__(**kwargs)

在以下代码中出现 args 时，即默认为以上 ModelConfig 参数配置

        我们来看一下其中的一些超参数的含义，比如dim是模型维度，n_layers是Transformer的层数，n_heads是注意力机制的头数，vocab_size是词汇表大小，max_seq_len是输入的最大序列长度等等。上面的代码中也对每一个参数做了详细的注释，在后面的代码中我们会根据这些超参数来构建我们的模型。

1.2.构建 RMSNorm

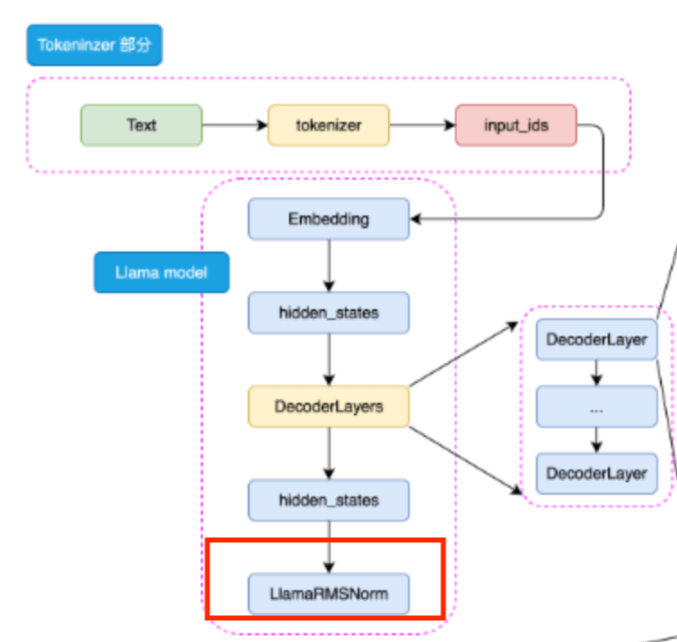
​​RMSNorm（Root Mean Square Layer Normalization，均方根层归一化）​​ 是深度学习，尤其是大语言模型（如 GPT 系列、LLaMA 等）中常用的一种高效且数值稳定的归一化方法。相比传统的 ​​LayerNorm​​，RMSNorm ​​不减去均值（centering）​​，只对输入的 ​​均方根（Root Mean Square, RMS）​​ 做归一化，因此计算更简单、推理更快，且通常效果相当甚至更好。

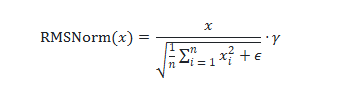
其中：

• xi 是输入向量的第 i 个元素
• γ 是可学习的缩放参数（对应代码中的 self.weight）
• n 是输入向量的维度数量
• ϵ 是一个小常数，用于数值稳定性（以避免除以零的情况）

这种归一化有助于通过确保权重的规模不会变得过大或过小来稳定学习过程，这在具有许多层的深度学习模型中特别有用。

class RMSNorm(nn.Module):def __init__(self, dim: int, eps: float):super().__init__()# eps是为了防止除以0的情况self.eps = eps# weight是一个可学习的参数，全部初始化为1self.weight = nn.Parameter(torch.ones(dim))def _norm(self, x):# 计算RMSNorm的核心部分# x.pow(2).mean(-1, keepdim=True)计算了输入x的平方的均值# torch.rsqrt是平方根的倒数，这样就得到了RMSNorm的分母部分，再加上eps防止分母为0# 最后乘以x，得到RMSNorm的结果return x * torch.rsqrt(x.pow(2).mean(-1, keepdim=True) + self.eps)def forward(self, x):# forward函数是模型的前向传播# 首先将输入x转为float类型，然后进行RMSNorm，最后再转回原来的数据类型# 最后乘以weight，这是RMSNorm的一个可学习的缩放因子output = self._norm(x.float()).type_as(x)return output * self.weight

1.3.构建 LLaMA2 Attention

在 LLaMA2 模型中，虽然只有 LLaMA2-70B模型使用了分组查询注意力机制（Grouped-Query Attention，GQA），但我们依然选择使用 GQA 来构建我们的 LLaMA Attention 模块，它可以提高模型的效率，并节省一些显存占用。

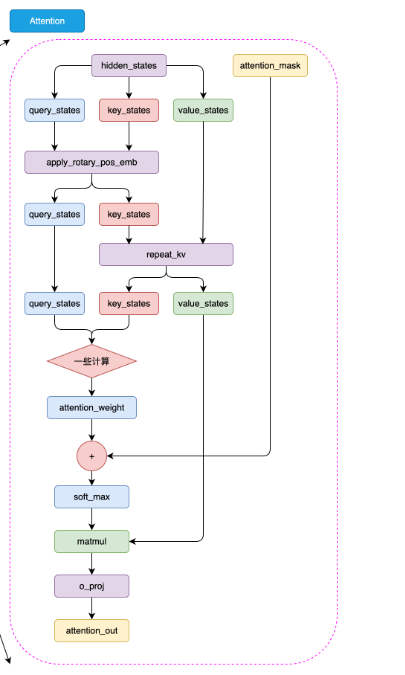
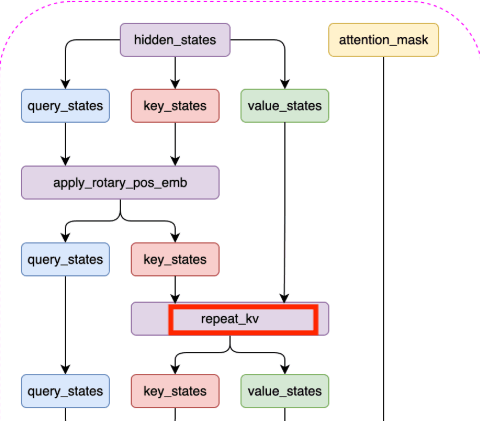
1.3.1.repeat_kv

​​处理 Key（K）和 Value（V）张量维度对齐问题​​ 的一个操作

参数名	类型	含义
x	torch.Tensor	输入张量，代表 ​​Key（K）或 Value（V）​​，来自多头注意力机制中的 K 或 V 投影后的结果
n_rep	int	​​重复次数​​，表示每个原始的“头”要复制多少份，通常是 num_query_heads // num_kv_heads，用来让 K/V 的头数与 Q 对齐

在 LLaMA2 模型中，我们需要将键和值的维度扩展到和查询的维度一样，这样才能进行注意力计算。我们可以通过如下代码实现repeat_kv：

def repeat_kv(x: torch.Tensor, n_rep: int) -> torch.Tensor:# 获取输入张量的形状：批量大小、序列长度、键/值对头的数量、每个头的维度大小bs, slen, n_kv_heads, head_dim = x.shape# 如果重复次数为1，则不需要重复，直接返回原始张量if n_rep == 1:return x# 对张量进行扩展和重塑操作以重复键值对return (x[:, :, :, None, :]  # 在第四个维度（头的维度前）添加一个新的维度.expand(bs, slen, n_kv_heads, n_rep, head_dim)  # 将新添加的维度扩展到n_rep大小，实现重复的效果.reshape(bs, slen, n_kv_heads * n_rep, head_dim)  # 重新塑形，合并键/值对头的数量和重复次数的维度)

在上述代码中：

• 首先，获取输入张量的形状：首先，代码通过 x.shape 获取输入张量的形状，包括批量大小（bs）、序列长度（slen）、键/值对头的数量（n_kv_heads）以及每个头的维度大小（head_dim）。

• 然后，检查重复次数：接着，代码检查重复次数 n_rep 是否为1。如果是1，则说明不需要对键和值进行重复，直接返回原始张量 x。

• 最后，扩展和重塑张量：

  • 在第三个维度（即键/值对头的维度）之后添加一个新的维度，形成 x[:, :, :, None, :]。
  • 使用 expand 方法将新添加的维度扩展到 n_rep 大小，实现键/值对的重复效果。
  • 最后，通过 reshape 方法重新塑形，将扩展后的维度合并回键/值对头的数量中，即 x.reshape(bs, slen, n_kv_heads * n_rep, head_dim)，这样最终的张量形状就达到了与查询维度一致的效果。

1.3.2.旋转嵌入

旋转嵌入（Rotary Position Embedding，RoPE）

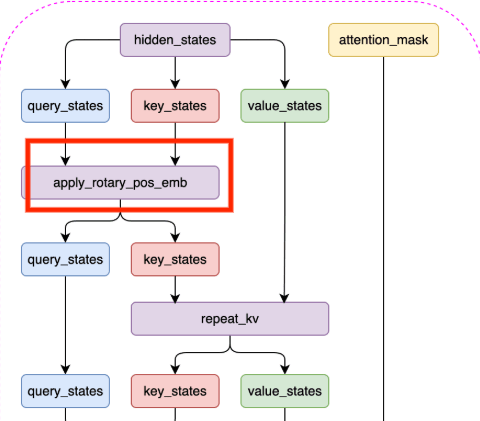
接着我们来实现旋转嵌入，旋转嵌入是 LLaMA2 模型中的一个重要组件，它可以为注意力机制提供更强的上下文信息，从而提高模型的性能。

首先，我们要构造获得旋转嵌入的实部和虚部的函数：

下面计算：

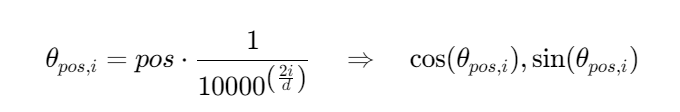
# 注意：此处的dim应为 dim//n_head，因为我们是对每个head进行旋转嵌入
def precompute_freqs_cis(dim: int, end: int, theta: float = 10000.0):# torch.arange(0, dim, 2)[: (dim // 2)].float()生成了一个从0开始，步长为2的序列，长度为dim的一半# 然后每个元素除以dim，再取theta的倒数，得到频率freqs = 1.0 / (theta ** (torch.arange(0, dim, 2)[: (dim // 2)].float() / dim))# 生成一个从0到end的序列，长度为endt = torch.arange(end, device=freqs.device)# 计算外积，得到一个二维矩阵，每一行是t的元素乘以freqs的元素freqs = torch.outer(t, freqs).float()# 计算频率的余弦值，得到实部freqs_cos = torch.cos(freqs)# 计算频率的正弦值，得到虚部freqs_sin = torch.sin(freqs)return freqs_cos, freqs_sin

最终，该函数返回两个矩阵 freqs_cos 和 freqs_sin，分别表示旋转嵌入的实部和虚部，用于后续的计算。

接着，我们来构造调整张量形状的reshape_for_broadcast函数，这个函数的主要目的是调整 freqs_cis 的形状，使其在进行广播操作时与 x 的维度对齐，从而能够进行正确的张量运算。

def reshape_for_broadcast(freqs_cis: torch.Tensor, x: torch.Tensor):# 获取x的维度数ndim = x.ndim# 断言，确保1在x的维度范围内assert 0 <= 1 < ndim# 断言，确保freqs_cis的形状与x的第二维和最后一维相同assert freqs_cis.shape == (x.shape[1], x.shape[-1])# 构造一个新的形状，除了第二维和最后一维，其他维度都为1，这样做是为了能够将freqs_cis与x进行广播操作shape = [d if i == 1 or i == ndim - 1 else 1 for i, d in enumerate(x.shape)]# 将freqs_cis调整为新的形状，并返回return freqs_cis.view(shape)

最后，我们可以通过如下代码实现旋转嵌入：

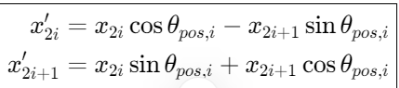
def apply_rotary_emb(xq: torch.Tensor,xk: torch.Tensor,freqs_cos: torch.Tensor,freqs_sin: torch.Tensor
) -> Tuple[torch.Tensor, torch.Tensor]:# 将查询和键张量转换为浮点数，并重塑形状以分离实部和虚部xq_r, xq_i = xq.float().reshape(xq.shape[:-1] + (-1, 2)).unbind(-1)xk_r, xk_i = xk.float().reshape(xk.shape[:-1] + (-1, 2)).unbind(-1)# 重新塑形频率张量以进行广播freqs_cos = reshape_for_broadcast(freqs_cos, xq_r)freqs_sin = reshape_for_broadcast(freqs_sin, xq_r)# 应用旋转，分别计算旋转后的实部和虚部xq_out_r = xq_r * freqs_cos - xq_i * freqs_sinxq_out_i = xq_r * freqs_sin + xq_i * freqs_cosxk_out_r = xk_r * freqs_cos - xk_i * freqs_sinxk_out_i = xk_r * freqs_sin + xk_i * freqs_cos# 将最后两个维度合并，并还原为原始张量的形状xq_out = torch.stack([xq_out_r, xq_out_i], dim=-1).flatten(3)xk_out = torch.stack([xk_out_r, xk_out_i], dim=-1).flatten(3)return xq_out.type_as(xq), xk_out.type_as(xk)

这里我们给出可以测试apply_rotary_emb函数的代码，大家也可以尝试在代码中添加断点，来查看每一步的计算结果。

xq = torch.randn(1, 50, 6, 48) # bs, seq_len, dim//n_head, n_head_dim
xk = torch.randn(1, 50, 6, 48) # bs, seq_len, dim//n_head, n_head_dim# 使用 precompute_freqs_cis 函数获取 sin和cos
cos, sin = precompute_freqs_cis(288//6, 50)
print(cos.shape, sin.shape)
xq_out, xk_out = apply_rotary_emb(xq, xk, cos, sin)xq_out.shape, xk_out.shape

1.3.3.组装LLaMA2 Attention

在上面我们已经完成了旋转嵌入的实现，接下来我们就可以构建 LLaMA2 Attention 模块了。

class Attention(nn.Module):def __init__(self, args: ModelConfig):super().__init__()# 根据是否指定n_kv_heads，确定用于键（key）和值（value）的头的数量。self.n_kv_heads = args.n_heads if args.n_kv_heads is None else args.n_kv_heads# 确保总头数可以被键值头数整除。assert args.n_heads % self.n_kv_heads == 0# 模型并行处理大小，默认为1。model_parallel_size = 1# 本地计算头数，等于总头数除以模型并行处理大小。self.n_local_heads = args.n_heads // model_parallel_size# 本地键值头数，等于键值头数除以模型并行处理大小。self.n_local_kv_heads = self.n_kv_heads // model_parallel_size# 重复次数，用于扩展键和值的尺寸。self.n_rep = self.n_local_heads // self.n_local_kv_heads# 每个头的维度，等于模型维度除以头的总数。self.head_dim = args.dim // args.n_heads# 定义权重矩阵。self.wq = nn.Linear(args.dim, args.n_heads * self.head_dim, bias=False)self.wk = nn.Linear(args.dim, self.n_kv_heads * self.head_dim, bias=False)self.wv = nn.Linear(args.dim, self.n_kv_heads * self.head_dim, bias=False)# 输出权重矩阵。self.wo = nn.Linear(args.n_heads * self.head_dim, args.dim, bias=False)# 定义dropout。self.attn_dropout = nn.Dropout(args.dropout)self.resid_dropout = nn.Dropout(args.dropout)# 保存dropout概率。self.dropout = args.dropout# 检查是否使用Flash Attention（需要PyTorch >= 2.0）。self.flash = hasattr(torch.nn.functional, 'scaled_dot_product_attention')if not self.flash:# 若不支持Flash Attention，则使用手动实现的注意力机制，并设置mask。print("WARNING: using slow attention. Flash Attention requires PyTorch >= 2.0")# 创建一个上三角矩阵，用于遮蔽未来信息。mask = torch.full((1, 1, args.max_seq_len, args.max_seq_len), float("-inf"))mask = torch.triu(mask, diagonal=1)# 注册为模型的缓冲区self.register_buffer("mask", mask)def forward(self, x: torch.Tensor, freqs_cos: torch.Tensor, freqs_sin: torch.Tensor):# 获取批次大小和序列长度，[batch_size, seq_len, dim]bsz, seqlen, _ = x.shape# 计算查询（Q）、键（K）、值（V）。xq, xk, xv = self.wq(x), self.wk(x), self.wv(x)# 调整形状以适应头的维度。xq = xq.view(bsz, seqlen, self.n_local_heads, self.head_dim)xk = xk.view(bsz, seqlen, self.n_local_kv_heads, self.head_dim)xv = xv.view(bsz, seqlen, self.n_local_kv_heads, self.head_dim)# 应用旋转位置嵌入（RoPE）。xq, xk = apply_rotary_emb(xq, xk, freqs_cos, freqs_sin)# 对键和值进行扩展以适应重复次数。xk = repeat_kv(xk, self.n_rep)xv = repeat_kv(xv, self.n_rep)# 将头作为批次维度处理。xq = xq.transpose(1, 2)xk = xk.transpose(1, 2)xv = xv.transpose(1, 2)# 根据是否支持Flash Attention，选择实现方式。if self.flash:# 使用Flash Attention。output = torch.nn.functional.scaled_dot_product_attention(xq, xk, xv, attn_mask=None, dropout_p=self.dropout if self.training else 0.0, is_causal=True)else:# 使用手动实现的注意力机制。scores = torch.matmul(xq, xk.transpose(2, 3)) / math.sqrt(self.head_dim)assert hasattr(self, 'mask')scores = scores + self.mask[:, :, :seqlen, :seqlen]scores = F.softmax(scores.float(), dim=-1).type_as(xq)scores = self.attn_dropout(scores)output = torch.matmul(scores, xv)# 恢复时间维度并合并头。output = output.transpose(1, 2).contiguous().view(bsz, seqlen, -1)# 最终投影回残差流。output = self.wo(output)output = self.resid_dropout(output)return output

同样大家可以使用下面的代码来对注意力模块进行测试，可以看到代码最终输出的形状为torch.Size([1, 50, 768])，与我们输入的形状一致，说明模块的实现是正确的。

# 创建Attention实例
attention_model = Attention(args)# 模拟输入数据
batch_size = 1
seq_len = 50  # 假设实际使用的序列长度为50
dim = args.dim
x = torch.rand(batch_size, seq_len, dim)  # 随机生成输入张量
# freqs_cos = torch.rand(seq_len, dim // 2)  # 模拟cos频率，用于RoPE
# freqs_sin = torch.rand(seq_len, dim // 2)  # 模拟sin频率，用于RoPEfreqs_cos, freqs_sin = precompute_freqs_cis(dim//args.n_heads, seq_len)# 运行Attention模型
output = attention_model(x, freqs_cos, freqs_sin)# attention出来之后的形状 依然是[batch_size, seq_len, dim]
print("Output shape:", output.shape)

1.4.构建 LLaMA2 MLP模块

​​多层感知机

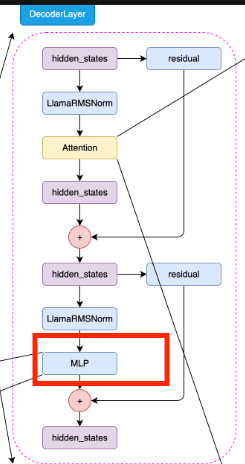
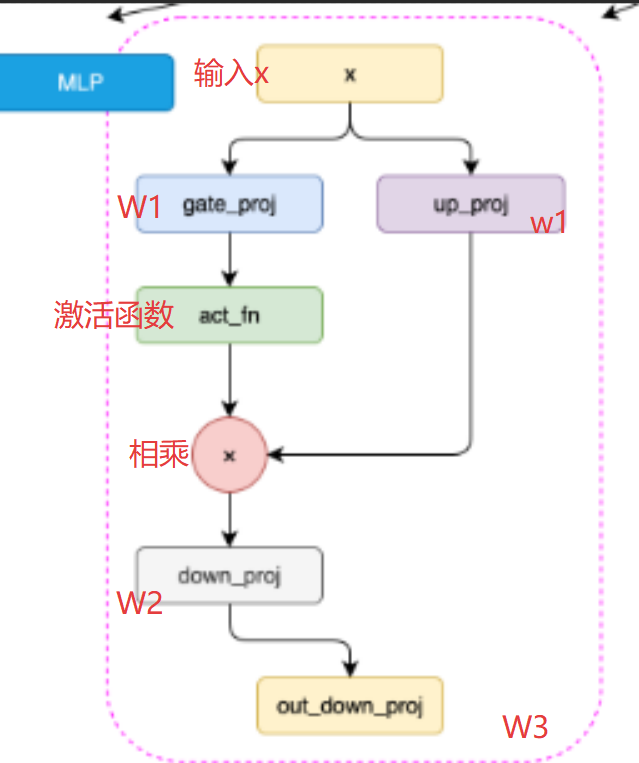
相对于前面我们实现的LLaMA2 Attention模块，LLaMA2 MLP模块的实现要简单一些。我们可以通过如下代码实现MLP：

class MLP(nn.Module):def __init__(self, dim: int, hidden_dim: int, multiple_of: int, dropout: float):super().__init__()# 如果没有指定隐藏层的维度，我们将其设置为输入维度的4倍# 然后将其减少到2/3，最后确保它是multiple_of的倍数if hidden_dim is None:hidden_dim = 4 * dimhidden_dim = int(2 * hidden_dim / 3)hidden_dim = multiple_of * ((hidden_dim + multiple_of - 1) // multiple_of)# 定义第一层线性变换，从输入维度到隐藏维度self.w1 = nn.Linear(dim, hidden_dim, bias=False)# 定义第二层线性变换，从隐藏维度到输入维度self.w2 = nn.Linear(hidden_dim, dim, bias=False)# 定义第三层线性变换，从输入维度到隐藏维度self.w3 = nn.Linear(dim, hidden_dim, bias=False)# 定义dropout层，用于防止过拟合self.dropout = nn.Dropout(dropout)def forward(self, x):# 前向传播函数# 首先，输入x通过第一层线性变换和SILU激活函数# 然后，结果乘以输入x通过第三层线性变换的结果# 最后，通过第二层线性变换和dropout层return self.dropout(self.w2(F.silu(self.w1(x)) * self.w3(x)))

1.5.LLaMA2 Decoder Layer

到这里，我们已经实现了LLaMA2模型的Attention模块和MLP模块，接下来我们就可以构建LLaMA2的Decoder Layer了。

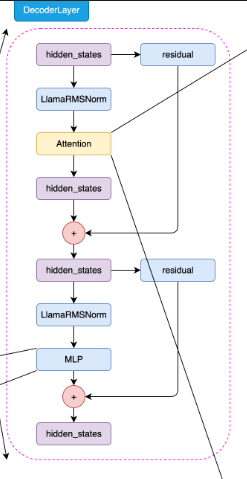
class DecoderLayer(nn.Module):def __init__(self, layer_id: int, args: ModelConfig):super().__init__()# 定义多头注意力的头数self.n_heads = args.n_heads# 定义输入维度self.dim = args.dim# 定义每个头的维度，等于输入维度除以头数self.head_dim = args.dim // args.n_heads# 定义LLaMA2Attention对象，用于进行多头注意力计算self.attention = Attention(args)# 定义LLaMAMLP对象，用于进行前馈神经网络计算self.feed_forward = MLP(dim=args.dim,hidden_dim=args.hidden_dim,multiple_of=args.multiple_of,dropout=args.dropout,)# 定义层的IDself.layer_id = layer_id# 定义注意力计算的归一化层self.attention_norm = RMSNorm(args.dim, eps=args.norm_eps)# 定义前馈神经网络计算的归一化层self.ffn_norm = RMSNorm(args.dim, eps=args.norm_eps)def forward(self, x, freqs_cos, freqs_sin):# 前向传播函数# 首先，输入x经过注意力归一化层，然后进行注意力计算，结果与输入x相加得到h# 然后，h经过前馈神经网络归一化层，然后进行前馈神经网络计算，结果与h相加得到输出