3.1 BP神经网络结构(反向传播算法)
BP神经网络(Back Propagation Neural Network,误差反向传播神经网络)是一种多层前馈神经网络,其核心特点在于利用“误差反向传播”算法进行训练。它的结构决定了其功能和能力。
一个典型的BP神经网络结构可以分为三个部分:
1.输入层
2.隐含层(一层或多层)
3.输出层
误差反向传播:当输出结果与真实值产生误差后,这个误差会沿着反方向(输出层 -> 隐含层 -> 输入层)传播,并根据误差来更新每一层的权重和偏置。这个过程是BP网络名称的由来和训练的核心
一、以2输入,2隐藏层,1个输出为例
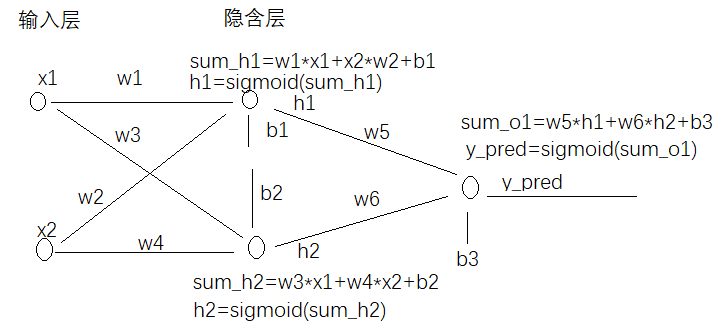
1.1 首先推导误差对w5,w6,b3的导数

1.2 继续推导误差对w1,w2,w3,w5,b1,b2的导数
二、例子代码
本案例输入为:超过平均值的体重、身高。一般男生体重身高都高于平均值,女生低于平均值。
import numpy as np
def sigmoid(x):return 1/(1+np.exp(-x))
def mse_loss(y_true,y_pred):return((y_true-y_pred)**2).mean()
def deriv_sigmoid(x):fx= sigmoid(x)return fx*(1-fx)class Neuron():def __init__(self,weights,bias):self.weights = weightsself.bias = biasdef feedforward(self,inputs):total = np.dot(self.weights,inputs) + self.biasreturn sigmoid(total)class OurNeuralNetworks():def __init__(self):weights = np.array([0,1])bias = 0self.h1 = Neuron(weights,bias)self.h2 = Neuron(weights,bias)self.o1 = Neuron(weights,bias)def feedforward(self,x):out_h1 = self.h1.feedforward(x)out_h2 = self.h2.feedforward(x)out_o1 = self.o1.feedforward(np.array([out_h1,out_h2]))return out_o1class OurNeuralNetwork2():def __init__(self):self.w1 = np.random.normal()self.w2 = np.random.normal()self.w3 = np.random.normal()self.w4 = np.random.normal()self.w5 = np.random.normal()self.w6 = np.random.normal()#biasself.b1 = np.random.normal()self.b2 = np.random.normal()self.b3 = np.random.normal()def feedforward(self,x):h1 = sigmoid(self.w1*x[0]+self.w2*x[1]+self.b1)h2 = sigmoid(self.w3 * x[0] + self.w4 * x[1] + self.b2)o1 = sigmoid(self.w5*h1 + self.w6*h2 + self.b3)return o1def train(self,data,all_y_trues):learn_rate = 0.1epochs=1000for epoch in range(epochs):for x, y_true in zip(data,all_y_trues):sum_h1 = self.w1 * x[0] + self.w2 * x[1] + self.b1h1 = sigmoid(sum_h1)sum_h2 = self.w3 * x[0] + self.w4 * x[1] + self.b2h2 = sigmoid(sum_h2)sum_o1 = self.w5 * h1 + self.w6 * h2 + self.b3o1 = sigmoid(sum_o1)y_pred = o1d_L_d_ypred = -2 * (y_true - y_pred)d_ypred_d_w5 = h1 * deriv_sigmoid(sum_o1)d_ypred_d_w6 = h2 * deriv_sigmoid(sum_o1)d_ypred_d_b3 = deriv_sigmoid(sum_o1)d_ypred_d_h1 = self.w5 * deriv_sigmoid(sum_o1)d_ypred_d_h2 = self.w6 * deriv_sigmoid(sum_o1)d_h1_d_w1 = x[0] * deriv_sigmoid(sum_h1)d_h1_d_w2 = x[1] * deriv_sigmoid(sum_h1)d_h1_d_b1 = deriv_sigmoid(sum_h1)d_h2_d_w3 = x[0] * deriv_sigmoid(sum_h2)d_h2_d_w4 = x[1] * deriv_sigmoid(sum_h2)d_h2_d_b2 = deriv_sigmoid(sum_h2)self.w5 -= learn_rate * d_L_d_ypred * d_ypred_d_w5self.w6 -= learn_rate * d_L_d_ypred * d_ypred_d_w6self.b3 -= learn_rate * d_L_d_ypred * d_ypred_d_b3self.w1 -= learn_rate * d_L_d_ypred * d_ypred_d_h1 * d_h1_d_w1self.w2 -= learn_rate * d_L_d_ypred * d_ypred_d_h1 * d_h1_d_w2self.b1 -= learn_rate * d_L_d_ypred * d_ypred_d_h1 * d_h1_d_b1self.w3 -= learn_rate * d_L_d_ypred * d_ypred_d_h2 * d_h2_d_w3self.w4 -= learn_rate * d_L_d_ypred * d_ypred_d_h2 * d_h2_d_w4self.b2 -= learn_rate * d_L_d_ypred * d_ypred_d_h2 * d_h2_d_b2if epoch % 10 == 0:y_preds = np.apply_along_axis(self.feedforward, 1, data)loss = mse_loss(all_y_trues, y_preds)print("Epoch %d loss: %.3f", (epoch, loss))data = np.array([[-2, -1], # Alice[25, 6], # Bob[17, 4], # Charlie[-15, -6] # diana
])all_y_trues = np.array([1, # Alice0, # Bob0, # Charlie1 # diana
])
network = OurNeuralNetwork2()
network.train(data, all_y_trues)emily = np.array([-7, -3]) # 128 pounds, 63 inches
frank = np.array([20, 2]) # 155 pounds, 68 inches
print("Emily: %.3f" % network.feedforward(emily)) # 0.951 - F
print("Frank: %.3f" % network.feedforward(frank)) # 0.039 - M结果满意:
Emily: 0.947
Frank: 0.039
