算法基础篇(4)枚举
枚举,顾名思义,就是把所有情况全部罗列出来,然后找出符合题目要求的那一个。因此,枚举是一种纯暴力的算法。一般情况下,枚举策略都是会超时的。此时要先根据题目的数据范围来判断暴力枚举是否可以通过。如果不行的话,就要用后面的各种算法来进行优化。
1、普通枚举
1.1 铺地毯
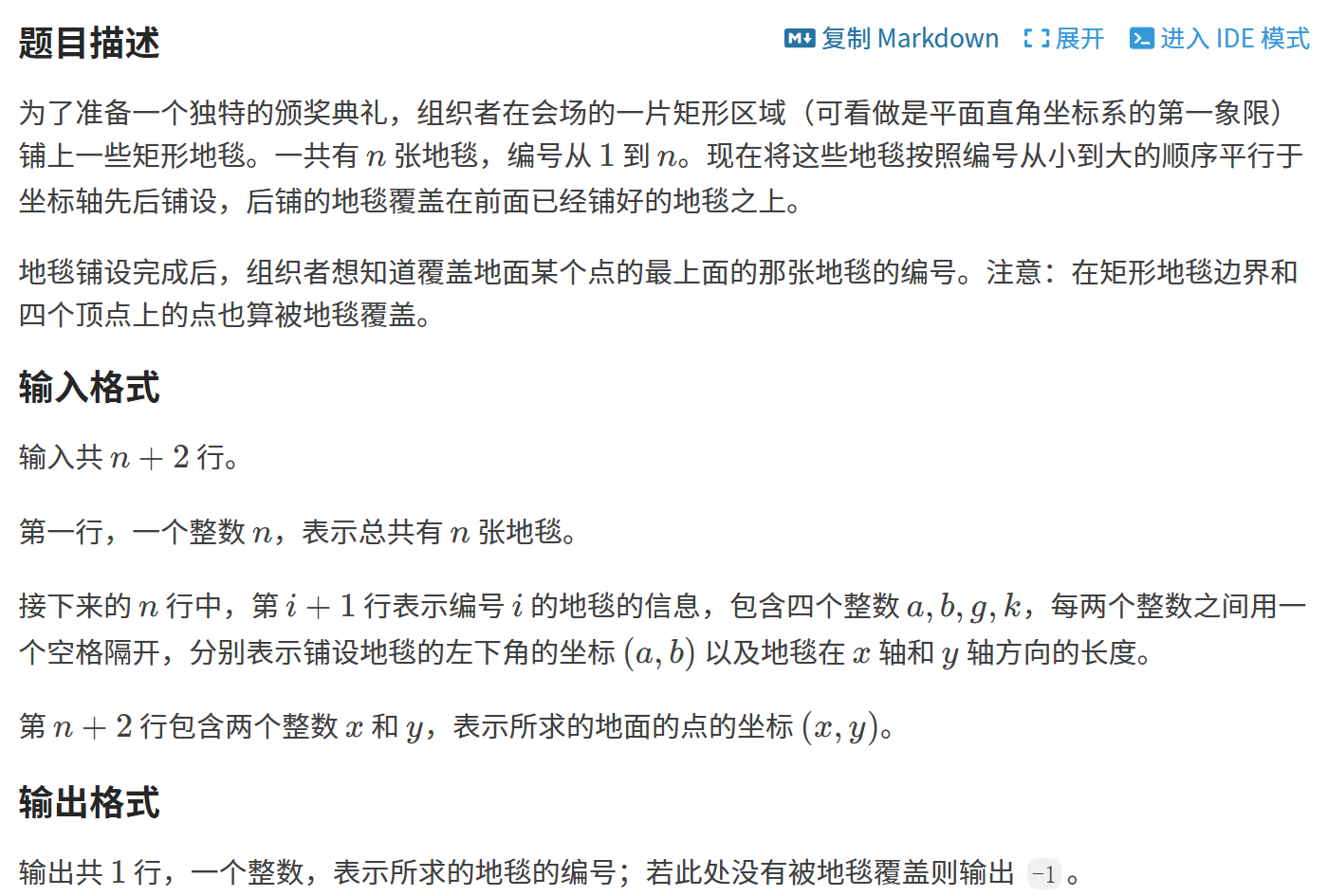
算法思路:枚举所有地毯,找出最后覆盖题目中点的那个地毯即可。
那么枚举的顺序是什么呢?如果从前往后枚举,我们至少要把所有地毯枚举完才能知道最终结果。但是如果逆序枚举的话,第一次找到的就是结果。
参考代码:
#define _CRT_SECURE_NO_WARNINGS 1
#include <iostream>
using namespace std;const int N = 1e4 + 10;int n;
int a[N], b[N], g[N], k[N];
int x, y;int find()
{//从后往前枚举for (int i = n;i >= 1;i--){//判断是否覆盖if (x >= a[i] && x <= a[i] + g[i] && y >= b[i] && y <= b[i] + k[i]){return i;}}return -1;
}int main()
{cin >> n;for (int i = 1;i <= n;i++){cin >> a[i] >> b[i] >> g[i] >> k[i];}cin >> x >> y;cout << find() << endl;return 0;
}1.2 回文日期
https://www.luogu.com.cn/problem/P2010
算法思路:这道题可以从以下三种方法中解决,这里更推荐使用第三种方法。
方法一:枚举x~y之间所有的数字,判断是否回文。如果回文,就拆分成年、月、日,判断是否是合法日期。
方法二:仅需枚举年份,然后拆分成回文形式的月、日,判断是否合法。
方法三:枚举所有的月、日,然后拼接成相应的年份,判断是否合法。那么这里需不需要判断闰年呢?不需要,因为2月29日(也就是0229)写成回文年份就是9220,是一个闰年。
参考代码:
#define _CRT_SECURE_NO_WARNINGS 1
#include <iostream>
using namespace std;int x, y;
int day[] = { 0,31,29,31,30,31,30,31,31,30,31,30,31 };int main()
{cin >> x >> y;int cnt = 0;//枚举日月的组合for (int i = 1;i <= 12;i++){for (int j = 1;j <= day[i];j++){int k = j % 10 * 1000 + j / 10 * 100 + i % 10 * 10 + i / 10;int num = k * 10000 + i * 100 + j;if (num >= x && num <= y){cnt++;}}}cout << cnt << endl;return 0;
}1.3 扫雷
https://www.luogu.com.cn/problem/P2327
算法思路:枚举第一列的第一个格子有没有放雷。
当第一行第一列的小格子状态确定之后,后续行的状态也跟着固定下来。因此,我们枚举第一行第一列的两种状态:要么有雷,要么没有雷,然后以此计算剩下的值,看是否满足题目所给数据。
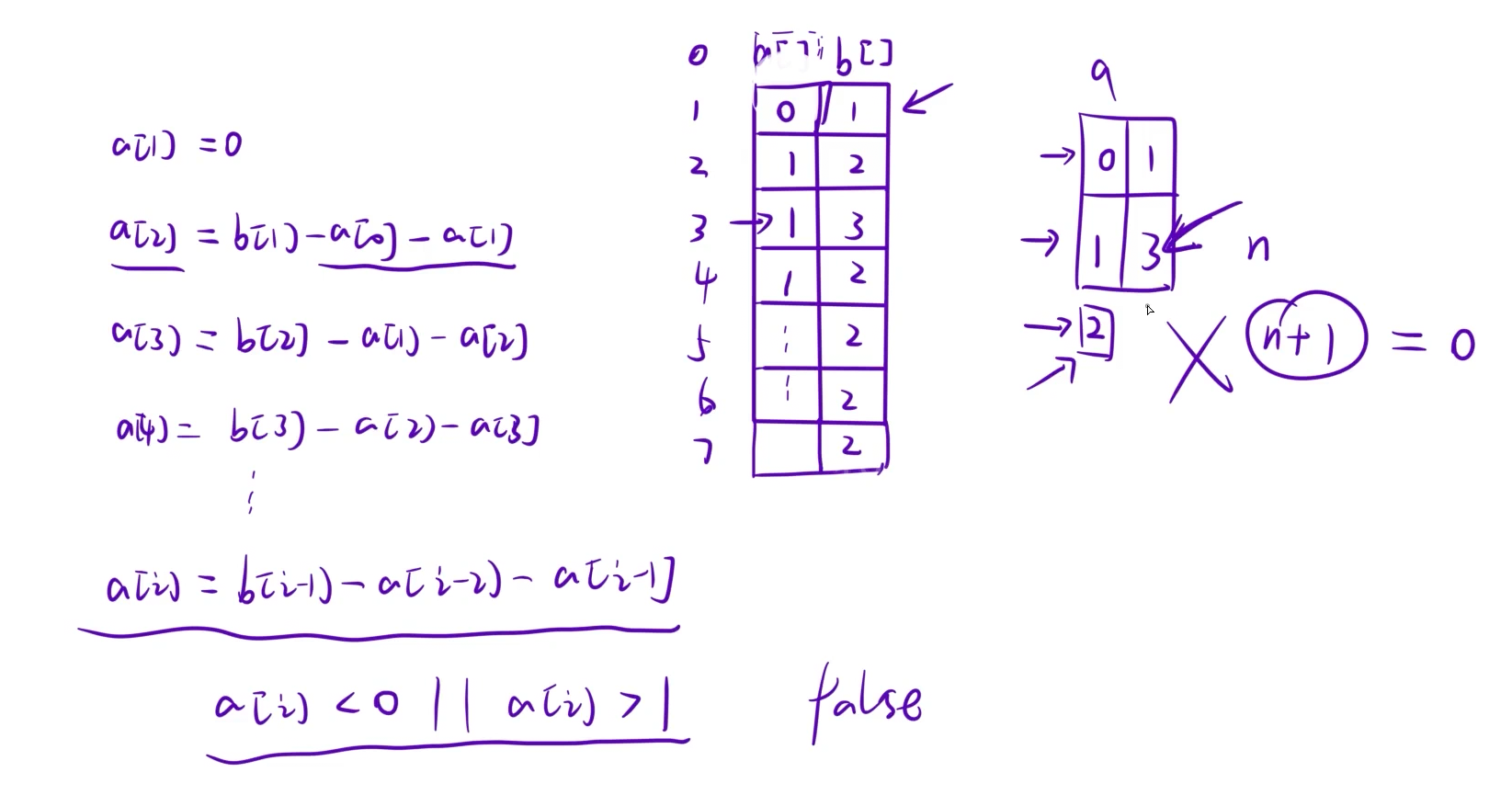
参考代码:
#define _CRT_SECURE_NO_WARNINGS 1
#include <iostream>
using namespace std;const int N = 1e4 + 10;int n;
int a[N], b[N];//不放地雷
int check1()
{a[1] = 0;for (int i = 2;i <= n + 1;i++){a[i] = b[i - 1] - a[i - 1] - a[i - 2];if (a[i] < 0 || a[i] > 1){return 0;}}if (a[n + 1] == 0)return 1;elsereturn 0;
}//放地雷
int check2()
{a[1] = 1;for (int i = 2;i <= n + 1;i++){a[i] = b[i - 1] - a[i - 1] - a[i - 2];if (a[i] < 0 || a[i] > 1){return 0;}}if (a[n + 1] == 0)return 1;elsereturn 0;
}int main()
{cin >> n;for (int i = 1;i <= n;i++){cin >> b[i];}int cnt = 0;cnt += check1(); //a[1]不放地雷cnt += check2(); //a[1]放地雷cout << cnt << endl;return 0;
}2、二进制枚举
二进制枚举:用一个数的二进制中的 0/1 表示两种状态,从而达到枚举各种情况。利用二进制枚举时,会运用到一些位运算的知识(关于位运算,可以去看算法基础篇(1))。关于利用二进制中0/1表示状态的这种方法,会在动态规划章节中的状态压缩dp中继续使用到。二进制枚举的方式也可以用递归实现。
2.1 子集

算法思路:运用二进制枚举的方式,把所有情况都枚举出来。

参考代码:
class Solution {
public:vector<vector<int>> subsets(vector<int>& nums) {vector<vector<int>> ret;size_t n = nums.size();//枚举所有状态for(int st = 0;st < (1 << n);st++){//根据 st 的状态,还原出要选的数vector<int> tmp; //存当前选的子集for(int i = 0;i < n;i++){if((st >> i) & 1){tmp.push_back(nums[i]);}}ret.push_back(tmp);}return ret;}
};2.2 费解的开关

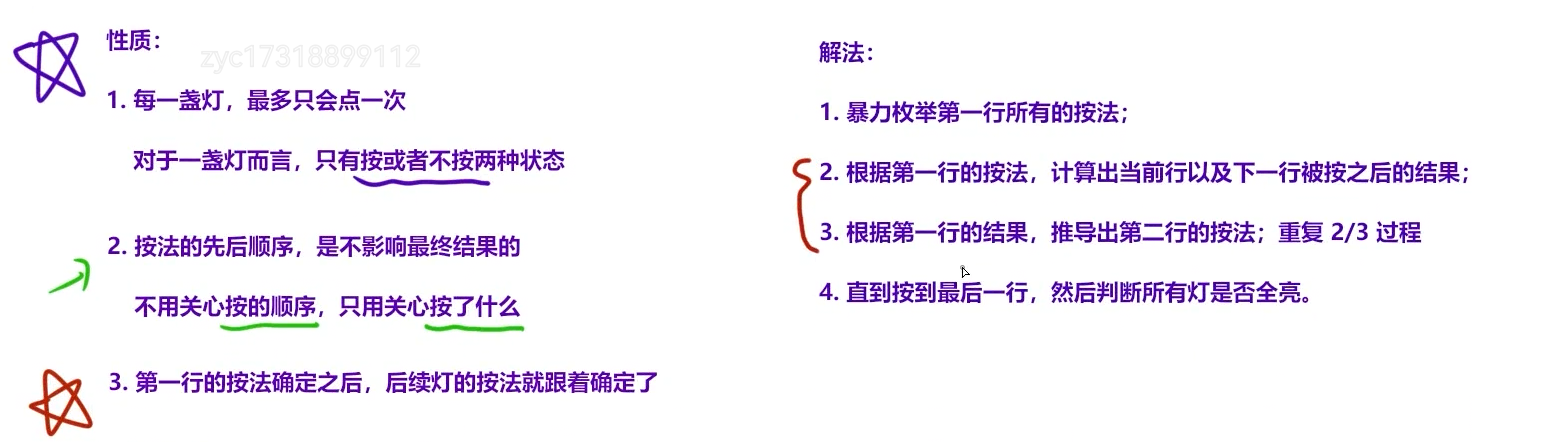
参考代码:
#define _CRT_SECURE_NO_WARNINGS 1
#include <iostream>
#include <cstring>
using namespace std;const int N = 10;
int n = 5;
int a[N]; //用二进制表示,来存储灯的状态
int t[N]; //备份a数组//计算x的二进制中一共有多少个1
int calc(int x)
{int count = 0;while (x){count++;x &= x - 1;}return count;
}int main()
{int T;cin >> T;while (T--){//多组测试时,一定要注意清空之前的数据memset(a, 0, sizeof(a));for (int i = 0;i < n;i++){for (int j = 0;j < n;j++){char ch;cin >> ch;//存成相反的if (ch == '0'){a[i] |= 1 << j;}}}int ret = 0x3f3f3f3f; //统计所有合法按法中的最小值//枚举第一行所有的按法for (int st = 0;st < (1 << n);st++){memcpy(t, a, sizeof(a));int push = st; //当前行的按法int cnt = 0; //统计当前按法下一共按了多少次//以此计算后续行的结果以及按法for (int i = 0;i < n;i++){cnt += calc(push);//修改当前行被按的结果t[i] = t[i] ^ push ^ (push << 1) ^ (push >> 1);t[i] = t[i] & ((1 << n) - 1); //清空影响//修改下一行的状态t[i + 1] = t[i + 1] ^ push;//下一行的按法push = t[i];}if (t[n - 1] == 0){ret = min(ret, cnt);}}if (ret > 6)cout << -1 << endl;elsecout << ret << endl;}return 0;
}