216. 组合总和 III
目录
题目链接:
题目:
解题思路:
代码:
总结:
题目链接:
216. 组合总和 III - 力扣(LeetCode)
题目:
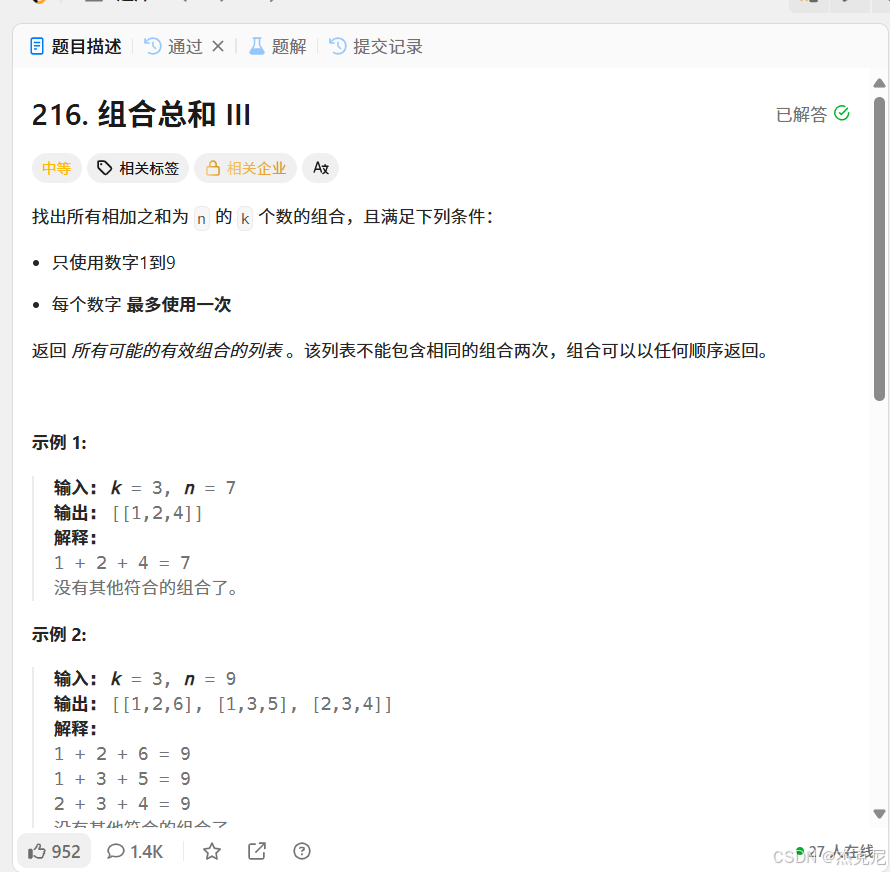
解题思路:
依旧回溯法
代码:
/*
*Stack Integer ArrayList String StringBuffer peek
*Collections imports LinkedList offer return
*empty polls offerLast pollFirst isEmpty
*List Deque append length HashMap null
*return
*/
class Solution {List<List<Integer>> res;List<Integer> path;public List<List<Integer>> combinationSum3(int k, int n) {res=new ArrayList<>();path=new ArrayList<>();find(1,n,k,0);return res;}public void find(int now,int n,int k,int sum){if(sum>n) return ;if(path.size()==k&&sum==n){res.add(new ArrayList<>(path));return ;}for(int i=now;i<=9-(k-path.size())+1;i++){path.add(i);find(i+1,n,k,sum+i);path.remove(path.size()-1);}}
}组合总和 III 算法深度解析:回溯法求解有限数字组合问题
组合总和 III 是 LeetCode 上的经典回溯算法问题,要求从 1 到 9 的数字中选出 k 个不重复的数字,使得它们的和等于 n。本文将详细解析一段高效求解该问题的代码,从算法设计、执行流程到优化策略,全方位理解回溯法在组合问题中的应用。
问题背景与需求分析
组合总和 III 问题可以描述为:
给定两个整数 k 和 n
需要从 1 到 9 的数字中选择 k 个不同的数字
使得这 k 个数字的和恰好等于 n
每个数字只能使用一次
返回所有可能的有效组合
例如,当 k=3,n=7 时,唯一有效的组合是 [1,2,4];当 k=3,n=9 时,有效组合包括 [1,2,6]、[1,3,5] 和 [2,3,4]。
这个问题的核心挑战在于:
确保组合中数字不重复
精确控制组合的长度为 k
保证组合的总和恰好为 n
高效穷举所有可能的组合而不重复
回溯法是解决这类组合搜索问题的最优策略,通过 "选择 - 递归 - 撤销" 的模式,能够系统性地探索所有可能的解。
代码整体结构解析
java
运行
import java.util.ArrayList;
import java.util.List;
class Solution {
// 存储所有符合条件的组合结果
List<List<Integer>> res;
// 存储当前正在构建的组合路径
List<Integer> path;
// 对外接口:输入k(数字个数)和n(目标和),返回所有有效组合
public List<List<Integer>> combinationSum3(int k, int n) {
res = new ArrayList<>();
path = new ArrayList<>();
// 启动回溯搜索:从1开始,目标和n,需要选k个,当前和0
find(1, n, k, 0);
return res;
}
// 回溯核心方法
public void find(int now, int n, int k, int sum) {
// 剪枝:如果当前和已经超过目标,直接返回
if (sum > n) return ;
// 终止条件:选够了k个数且和等于n
if (path.size() == k && sum == n) {
res.add(new ArrayList<>(path));
return ;
}
// 循环选择数字,带剪枝优化
for(int i = now; i <= 9 - (k - path.size()) + 1; i++){
path.add(i); // 选择当前数字
find(i + 1, n, k, sum + i); // 递归探索
path.remove(path.size() - 1); // 撤销选择(回溯)
}
}
}
这段代码采用标准的回溯法框架,主要包含两个部分:
对外接口combinationSum3:负责初始化结果集和路径,启动回溯过程
回溯核心方法find:实现 "选择 - 递归 - 撤销" 的核心逻辑,是算法的核心
代码中定义了两个关键变量:
res:用于存储所有符合条件的组合结果,是最终要返回的列表
path:用于记录当前正在构建的组合路径,随着回溯过程动态变化
核心变量与初始化逻辑
变量定义解析
java
运行
List<List<Integer>> res; // 结果集
List<Integer> path; // 当前路径
res是一个二维列表,每个元素都是一个符合条件的组合(长度为 k 的列表)
path是一个一维列表,用于临时存储正在构建的组合,在回溯过程中不断被修改
这两个变量的设计体现了回溯算法的典型思路:用一个临时变量记录当前状态,当找到有效解时,将当前状态的副本存入结果集。
初始化过程
java
运行
public List<List<Integer>> combinationSum3(int k, int n) {
res = new ArrayList<>();
path = new ArrayList<>();
find(1, n, k, 0);
return res;
}
初始化过程非常关键:
每次调用方法时都要重新初始化res和path,避免多次调用时的状态污染
调用find方法启动回溯,传入初始参数:
now=1:从数字 1 开始选择(因为数字范围是 1-9)
n:目标和
k:需要选择的数字个数
sum=0:当前组合的总和,初始为 0
回溯核心方法find深度解析
find方法是整个算法的核心,实现了回溯法的 "选择 - 递归 - 撤销" 三部曲,同时包含了关键的剪枝优化。我们逐部分解析其逻辑。
参数说明
java
运行
public void find(int now, int n, int k, int sum)
方法的四个参数各有明确用途:
now:当前可以选择的起始数字(用于避免重复组合)
n:目标和(需要达到的总和)
k:需要选择的数字总数
sum:当前组合的数字总和(已选择数字的累加和)
这些参数共同控制着回溯过程的状态,确保算法能够正确、高效地搜索所有可能的组合。
剪枝优化:提前终止无效路径
java
运行
if (sum > n) return ;
这是一个关键的剪枝条件:当当前组合的总和已经超过目标和 n 时,继续添加数字只会让总和更大,不可能得到有效解。此时直接返回,终止当前路径的搜索,避免无效的递归调用。
剪枝是回溯算法提高效率的核心手段,能够大幅减少不必要的计算。这个简单的判断可以在很多情况下提前终止搜索,尤其是当 n 较小时效果显著。
终止条件:收集有效组合
java
运行
if (path.size() == k && sum == n) {
res.add(new ArrayList<>(path));
return ;
}
这是回溯过程的终止条件,当同时满足两个条件时:
当前路径的长度等于 k(已经选择了 k 个数字)
当前组合的总和等于 n(满足和的要求)
此时说明找到了一个有效组合,需要将其加入结果集。这里有个关键细节:res.add(new ArrayList<>(path))而不是res.add(path)。
为什么要创建副本?因为path是一个引用类型,在后续的回溯过程中会被不断修改。如果直接添加引用,当path变化时,res中已存储的组合也会跟着变化。创建副本可以确保res中存储的是当前状态的快照,避免后续修改的影响。
循环选择与回溯过程
java
运行
for(int i = now; i <= 9 - (k - path.size()) + 1; i++){
path.add(i); // 选择当前数字
find(i + 1, n, k, sum + i); // 递归探索
path.remove(path.size() - 1); // 撤销选择(回溯)
}
这部分是回溯算法的核心逻辑,包含三个关键步骤:选择、递归、撤销,我们逐一解析。
循环范围:带剪枝的选择空间
循环的起始条件是i = now,这确保了:
数字不会被重复选择(每次选择都从当前数字之后开始)
组合不会重复(如 [1,2] 和 [2,1] 不会同时出现,因为只能从左到右选择)
循环的终止条件i <= 9 - (k - path.size()) + 1是一个精妙的剪枝优化:
k - path.size():还需要选择的数字个数
9 - (k - path.size()) + 1:确保有足够的数字可供选择
例如,当还需要选择 2 个数字时(k - path.size() = 2),最后一个可选择的数字是 8(因为 9-2+1=8),选择 8 后还能选 9;如果选择 9,就没有下一个数字可选了,无法满足还需 2 个数字的要求。
这个剪枝条件大幅减少了循环的次数,尤其在组合长度较大时效果明显。
选择:添加当前数字到路径
java
运行
path.add(i); // 选择当前数字
将当前数字 i 添加到路径中,标记为 "已选择"。这一步改变了当前状态,为下一步递归做准备。
递归:探索下一层选择
java
运行
find(i + 1, n, k, sum + i); // 递归探索
递归调用find方法,探索选择 i 之后的所有可能组合:
参数i + 1:下一次选择必须从 i+1 开始,确保数字不重复
参数sum + i:更新当前总和,加上刚刚选择的数字 i
这一步体现了回溯算法的 "深度优先" 特性,不断深入探索每一个可能的选择。
撤销:回溯到上一步状态
java
运行
path.remove(path.size() - 1); // 撤销选择(回溯)
这是回溯算法的关键步骤,在递归返回后,将刚刚添加的数字从路径中移除,恢复到选择之前的状态,以便尝试下一个可能的数字。
path.size() - 1确保我们总是移除最后添加的数字,这是栈式的操作方式,符合 "后进先出" 的原则。
算法执行流程示例
为了更直观地理解算法的工作原理,我们以k=3, n=9为例,详细模拟算法的执行流程。
初始调用
java
运行
find(1, 9, 3, 0); // now=1, n=9, k=3, sum=0, path=[]
第一层递归(path.size ()=0)
循环i从 1 到9 - (3-0) + 1 = 7(i=1 到 7)
i=1 分支
path.add(1) → path=[1]
调用 find (2, 9, 3, 1)
第二层递归(path.size ()=1)
循环i从 2 到9 - (3-1) + 1 = 8(i=2 到 8)
i=2 分支
path.add(2) → path=[1,2]
调用 find (3, 9, 3, 3)
第三层递归(path.size ()=2)
循环i从 3 到9 - (3-2) + 1 = 9(i=3 到 9)
i=6 分支
path.add(6) → path=[1,2,6]
sum=1+2+6=9,path.size()=3
满足条件,添加 [1,2,6] 到 res
返回,执行 path.remove → path=[1,2]
其他 i 值
i=3:sum=1+2+3=6 < 9 → 不满足
i=4:sum=7 < 9 → 不满足
i=5:sum=8 < 9 → 不满足
i=6:满足条件(已记录)
i=7:sum=10 > 9 → 触发剪枝
... 后续 i 值都会触发剪枝
回到第二层递归,继续 i=3 分支
i=3 分支
path.add(3) → path=[1,3]
调用 find (4, 9, 3, 4)
在第三层递归中,i=5 时:
path.add(5) → path=[1,3,5]
sum=1+3+5=9,满足条件,添加到 res
以此类推...
最终结果
经过完整的回溯过程,最终 res 将包含所有符合条件的组合:
plaintext
[[1,2,6], [1,3,5], [2,3,4]]
这个过程清晰地展示了回溯算法如何系统性地探索所有可能的组合,通过剪枝避免无效路径,通过撤销操作回溯到上一状态,最终找到所有有效解。
算法复杂度分析
时间复杂度
在最坏情况下,算法需要探索所有可能的组合,时间复杂度为 O (C (9, k)),即从 9 个数字中选择 k 个的组合数。因为 9 是一个固定的小数字(最大为 9),所以时间复杂度实际上是一个常数级别 O (1)。
具体来说,当 k=5 时,组合数 C (9,5)=126;当 k=9 时,组合数为 1。因此算法的实际运行效率非常高。
空间复杂度
空间复杂度主要取决于两个因素:
递归调用栈的深度:最大为 k(需要选择 k 个数字)
存储结果的空间:最多为 C (9, k) 个组合,每个组合包含 k 个元素
因此空间复杂度为 O (k * C (9, k)),同样由于 9 是固定的小数字,空间复杂度也是常数级别 O (1)。
代码优化策略分析
这段代码已经包含了两处关键的优化策略,使其效率达到最优:
1. 提前剪枝(sum > n)
当当前组合的总和已经超过目标 n 时,立即终止递归,避免继续添加数字导致的无效计算。这个优化在 n 较小时效果尤为明显,能减少大量不必要的递归调用。
2. 循环范围剪枝(i <= 9 - (k - path.size ()) + 1)
通过计算剩余所需数字的数量,动态调整循环的终止条件,确保有足够的数字可供选择,避免了选择到后期发现数字不足的情况。
这两种剪枝策略的结合,使得算法在实际运行中效率很高,即使对于最大的输入规模(k=9, n=45)也能快速得到结果。
与其他解法的对比
组合总和 III 问题还可以用其他方法解决,比如暴力枚举法,但回溯法是最优的选择:
与暴力枚举相比:
暴力枚举需要生成所有可能的 k 个数字组合,然后检查其和是否等于 n
回溯法通过剪枝可以提前排除无效组合,效率更高
回溯法的代码更简洁,扩展性更好
与动态规划相比:
动态规划适合解决计数问题(如 "有多少种组合"),但不适合生成所有具体组合
对于需要返回所有具体解的问题,回溯法是更自然的选择
因此,回溯法是解决组合总和 III 问题的最优策略,既能高效搜索所有可能的解,又能通过剪枝优化提高效率。
可能的扩展与变体
这段代码可以轻松扩展以解决类似的组合问题:
改变数字范围:如果需要从 1 到 m 而不是 1 到 9 选择数字,只需将循环条件中的 9 改为 m 即可
允许数字重复选择:如果允许重复选择同一数字,只需将递归参数 i+1 改为 i 即可
增加数字集合:如果数字不是连续的 1-9,而是给定的数字集合,只需循环遍历该集合并添加去重逻辑
例如,允许重复选择的版本只需修改一行代码:
java
运行
// 原代码(不允许重复)
find(i + 1, n, k, sum + i);
// 修改后(允许重复)
find(i, n, k, sum + i);
这种灵活性体现了回溯算法的强大之处,通过微小的调整就能适应不同的问题需求。
总结
本文详细解析了组合总和 III 问题的回溯法解决方案,从代码结构、核心逻辑到执行流程,全方位展示了回溯算法的工作原理。这段代码虽然简短,但包含了丰富的算法思想:
回溯法的 "选择 - 递归 - 撤销" 核心模式
有效的剪枝策略,大幅提高算法效率
利用引用类型的特性,通过副本保存中间结果
控制循环范围,避免重复组合
理解这个算法不仅能解决组合总和 III 问题,更能掌握回溯法的通用思想,为解决其他组合、排列、子集问题打下基础。回溯法作为一种重要的算法思想,在搜索问题、优化问题中有着广泛的应用,掌握它对于提升算法能力至关重要。
通过这个例子我们可以看到,优秀的算法往往是简洁而高效的,通过巧妙的状态控制和剪枝策略,能够在复杂的搜索空间中快速找到所有有效解。
总结:
本文解析了LeetCode 216题"组合总和III"的回溯算于n。算法采用回溯框架,通过选择-递归-撤销三步曲探索所有可能组合,并运用两项关键优化:1)当和超过n时提前终止;2)动态调整数字选择范围避免无效搜索。代码结构清晰,包含结果集res和当前路径path两个核心变量,通过深度优先搜索和剪枝策略高效求得所有解。该解法时间复杂度为组合数C(9,k),空间复杂度为O(k*C(9,k)),是解决此类组合问题的经典方法。法解决方案。该问题要求在1-9中找出k个不重复数字,使其和等
