669. 修剪二叉搜索树
目录
题目链接:
题目:
解题思路:
代码:
总结:
题目链接:
669. 修剪二叉搜索树 - 力扣(LeetCode)
题目:
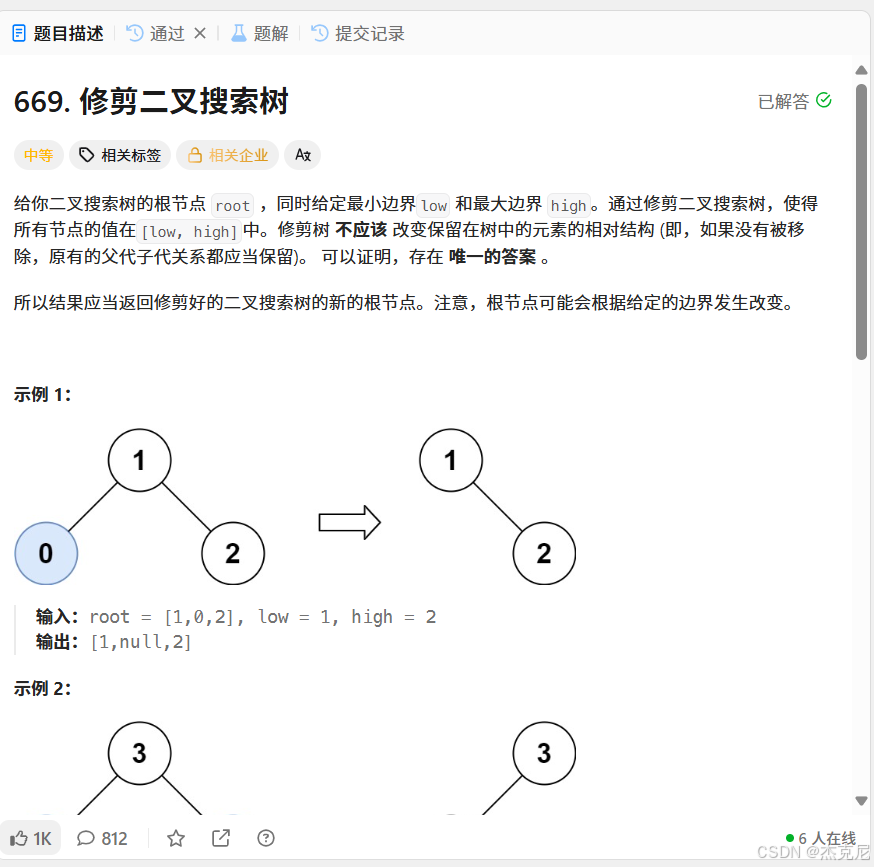
解题思路:
使用后序遍历,从根部开始往上一次处理,然后就是上一个博客一样的处理情况
代码:
/*** Definition for a binary tree node.* public class TreeNode {* int val;* TreeNode left;* TreeNode right;* TreeNode() {}* TreeNode(int val) { this.val = val; }* TreeNode(int val, TreeNode left, TreeNode right) {* this.val = val;* this.left = left;* this.right = right;* }* }*/
class Solution {public TreeNode trimBST(TreeNode root, int low, int high) {if(root==null) return null;root.left=trimBST(root.left,low,high);root.right=trimBST(root.right,low,high);if(root.val<low||root.val>high){if(root.left==null&&root.right==null) return n ull;else if(root.left!=null&&root.right==null) return root.left;else if(root.left==null&&root.right!=null) return root.right;else{TreeNode node=root.right;while(node.left!=null) node=node.left;node.left=root.left;return root.right;}}return root;}
}深入解析二叉搜索树修剪算法(trimBST)的实现与原理
在二叉搜索树(BST)的操作中,修剪操作是一个重要的功能,它能够移除所有值不在指定范围内的节点,同时保持 BST 的特性。本文将详细解析一段二叉搜索树修剪算法的代码,探讨其实现逻辑、执行流程以及背后的设计思想。
二叉搜索树修剪的基本概念
二叉搜索树的修剪(trim)指的是:给定一个范围 [low, high],移除二叉搜索树中所有值小于 low 或大于 high 的节点,并且保证修剪后的树仍然是一棵有效的二叉搜索树。
修剪操作需要满足两个核心要求:
修剪后的树只包含值在 [low, high] 范围内的节点
必须保持二叉搜索树的特性(左子树值 < 根节点值 < 右子树值)
代码整体结构
java
运行
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public TreeNode trimBST(TreeNode root, int low, int high) {
if(root==null) return null;
root.left=trimBST(root.left,low,high);
root.right=trimBST(root.right,low,high);
if(root.val<low||root.val>high){
if(root.left==null&&root.right==null) return null;
else if(root.left!=null&&root.right==null) return root.left;
else if(root.left==null&&root.right!=null) return root.right;
else{
TreeNode node=root.right;
while(node.left!=null) node=node.left;
node.left=root.left;
return root.right;
}
}
return root;
}
}
这段代码采用递归方式实现二叉搜索树的修剪,整体逻辑分为三个主要步骤:
递归修剪左子树
递归修剪右子树
判断并处理当前节点是否需要被修剪
关键代码逐行解析
递归终止条件
java
运行
if(root==null) return null;
这是递归的基本终止条件。当遇到空节点时,直接返回 null,表示这个位置不需要任何节点。
修剪左子树
java
运行
root.left=trimBST(root.left,low,high);
这行代码递归地修剪当前节点的左子树,并将修剪后的左子树结果重新赋值给当前节点的左指针。这确保了左子树中所有不符合条件的节点都已被移除。
修剪右子树
java
运行
root.right=trimBST(root.right,low,high);
类似地,这行代码递归地修剪当前节点的右子树,并将修剪后的结果重新赋值给当前节点的右指针。
判断当前节点是否需要修剪
java
运行
if(root.val<low||root.val>high){
// 处理当前节点需要被修剪的情况
}
这是修剪操作的核心判断:如果当前节点的值小于 low 或大于 high,则该节点需要被移除(修剪掉)。
根据当前节点被移除后,其左右子树的不同情况,代码分为四种处理方式:
情况 1:左右子树都为空
java
运行
if(root.left==null&&root.right==null) return null;
如果当前节点是叶子节点(左右子树都为空),且需要被修剪,则直接返回 null,表示这个位置不再有节点。
情况 2:只有左子树不为空
java
运行
else if(root.left!=null&&root.right==null) return root.left;
如果当前节点需要被修剪,且只有左子树存在,则返回左子树。这相当于用左子树替代了当前节点的位置,保持了树的连续性。
情况 3:只有右子树不为空
java
运行
else if(root.left==null&&root.right!=null) return root.right;
类似地,如果当前节点需要被修剪,且只有右子树存在,则返回右子树,用右子树替代当前节点的位置。
情况 4:左右子树都不为空
java
运行
else{
TreeNode node=root.right;
while(node.left!=null) node=node.left;
node.left=root.left;
return root.right;
}
这是最复杂的一种情况,当前节点需要被修剪,且左右子树都存在。处理方式如下:
找到右子树中最左侧的节点(即右子树中值最小的节点)
将当前节点的左子树连接到这个最小节点的左指针上
返回当前节点的右子树作为新的子树根节点
这种处理方式保证了修剪后仍然维持二叉搜索树的特性:原左子树的所有值都小于右子树最小节点的值,因此可以安全地连接到其左子树。
保留当前节点
java
运行
return root;
如果当前节点的值在 [low, high] 范围内,则不需要修剪,直接返回当前节点。
算法执行流程示例
为了更好地理解修剪过程,我们通过一个具体示例来模拟算法的执行:
假设初始二叉搜索树结构如下:
plaintext
3
/ \
0 4
\
2
/
1
修剪范围为 [1, 3](即保留值在 1 到 3 之间的节点)
执行流程:
从根节点 3 开始,首先递归修剪左子树(根为 0)和右子树(根为 4)
修剪左子树(根为 0):
递归修剪 0 的左子树(null)和右子树(根为 2)
修剪右子树(根为 2):
递归修剪 2 的左子树(根为 1)和右子树(null)
修剪左子树(根为 1):
1 的值在范围内,返回 1
2 的值在范围内,返回 2(其左子树已修剪为 1)
0 的值(0 < 1)需要被修剪:
0 的右子树不为空(根为 2)
返回右子树(根为 2)
根节点 3 的左子树更新为 2
修剪右子树(根为 4):
4 的值(4 > 3)需要被修剪:
4 的左右子树都为空
返回 null
根节点 3 的右子树更新为 null
处理根节点 3:
3 的值在范围内,不需要修剪
返回 3
最终修剪后的树结构:
plaintext
3
/
2
/
1
算法设计思想分析
后序遍历的应用
该算法采用了后序遍历的思想:先处理左子树,再处理右子树,最后处理当前节点。这种顺序的优势在于:
在判断当前节点是否需要修剪前,左右子树已经完成了修剪
处理当前节点时,可以直接使用修剪后的左右子树结果
确保了所有子树都已符合条件后,再决定当前节点的去留
利用 BST 特性的优化
虽然代码没有显式地利用 BST"左小右大" 的特性进行剪枝,但在处理左右子树都存在的情况时,通过寻找右子树最小值节点来连接左子树,正是利用了 BST 的特性,保证了修剪后的树仍然是有效的 BST。
递归的优势
递归实现使得代码简洁明了,每一层递归只关注当前节点的处理,符合 "分而治之" 的思想:
将大问题(修剪整棵树)分解为小问题(修剪左子树、右子树和当前节点)
每个小问题的解决方式相同
通过递归调用自底向上地构建解决方案
时间复杂度与空间复杂度
时间复杂度
算法的时间复杂度为 O (n),其中 n 是二叉树的节点总数。在最坏情况下,需要访问树中的每个节点一次,例如当所有节点都需要被修剪或所有节点都需要被保留时。
空间复杂度
空间复杂度为 O (h),其中 h 是二叉树的高度。这是由于递归调用栈的深度最多为树的高度:
在平衡二叉树中,h = log n,空间复杂度为 O (log n)
在最坏情况下(树退化为链表),h = n,空间复杂度为 O (n)
与其他修剪方法的对比
另一种常见的修剪思路是先判断当前节点是否需要保留,再决定修剪方向:
如果当前节点值 < low:直接返回右子树的修剪结果
如果当前节点值 > high:直接返回左子树的修剪结果
否则:分别修剪左右子树
两种方法各有优势:
本文解析的方法采用后序遍历,逻辑上更符合 "先处理子树再处理自身" 的思维
另一种方法更积极地利用 BST 特性,可以提前终止某些子树的遍历,在某些情况下更高效
但两种方法的时间复杂度和空间复杂度是相同的。
可能的错误与边界情况
空树处理:代码正确处理了空树情况(root == null 时返回 null)
单节点树:如果单节点值在范围内则保留,否则返回 null
所有节点都需要修剪:最终返回 null
所有节点都不需要修剪:返回原树结构
边界值处理:值等于 low 或 high 的节点会被保留
总结
本文解析的二叉搜索树修剪算法通过后序遍历的递归方式,实现了对二叉搜索树的高效修剪。算法的核心思想是:先递归修剪左右子树,再根据当前节点值决定是否保留该节点。当需要移除节点时,根据其左右子树的存在情况,采用不同的处理策略,确保修剪后的树仍然保持二叉搜索树的特性。
该算法的优势在于:
逻辑清晰,实现简洁
正确处理了所有可能的节点情况
保持了二叉搜索树的特性
时间和空间复杂度均处于较优水平
理解这个算法不仅有助于掌握二叉搜索树的修剪操作,也能加深对后序遍历和递归思想的理解,为处理更复杂的树结构问题提供参考。
总结:
本文解析了二叉搜索树的修剪算法trimBST,该算法通过后序遍历递归处理,先修剪左右子树再判断当前节点。核心逻辑是:若节点值超出范围[low,high],则根据子树情况执行不同处理策略:当左右子树均存在时,将左子树连接到右子树的最小节点下。该算法时间复杂度O(n),空间复杂度O(h),能有效保持BST特性,正确处理空树、单节点等边界情况,体现了分治思想和BST特性的巧妙运用。
