当前位置：首页 > news >正文

支持向量机深度解析：从数学原理到工程实践的完整指南

news 2025/9/22 8:41:13

在这里插入图片描述

🌟 Hello，我是蒋星熠Jaxonic！
🌈 在浩瀚无垠的技术宇宙中，我是一名执着的星际旅人，用代码绘制探索的轨迹。
🚀 每一个算法都是我点燃的推进器，每一行代码都是我航行的星图。
🔭 每一次性能优化都是我的天文望远镜，每一次架构设计都是我的引力弹弓。
🎻 在数字世界的协奏曲中，我既是作曲家也是首席乐手。让我们携手，在二进制星河中谱写属于极客的壮丽诗篇！

摘要

作为一名在机器学习领域摸爬滚打多年的技术实践者，我深深被支持向量机（Support Vector Machine, SVM）的数学之美所震撼。SVM不仅仅是一个分类算法，更是统计学习理论的完美体现，它将复杂的优化问题转化为优雅的几何解释，让我们能够在高维空间中找到最优的决策边界。

在我的项目实践中，SVM展现出了令人惊叹的泛化能力和鲁棒性。从文本分类到图像识别，从生物信息学到金融风控，SVM都能够提供稳定可靠的解决方案。其核心思想是寻找能够最大化分类间隔的超平面，这种"最大间隔"的思想不仅保证了模型的泛化性能，更体现了奥卡姆剃刀原理在机器学习中的应用。

SVM的魅力在于其完美的理论基础和实用性的结合。通过拉格朗日对偶理论，我们可以将原始的约束优化问题转化为对偶问题，从而引入核技巧（Kernel Trick），使得SVM能够处理非线性可分的数据。这种数学上的优雅转换，让我每次重新审视时都会感到由衷的敬佩。

本文将从SVM的数学基础出发，深入探讨其核心算法原理，并结合实际的工程实践，全面解析SVM在现代机器学习中的应用。我将分享在调参优化、核函数选择、以及大规模数据处理等方面的实战经验，帮助读者构建完整的SVM技术体系，在机器学习的征途中更加游刃有余。

1. SVM核心原理与数学基础

1.1 线性可分SVM的几何直觉

支持向量机的核心思想是在特征空间中寻找一个超平面，使得不同类别的样本被正确分开，并且分类间隔最大化。这个看似简单的想法背后蕴含着深刻的数学原理。

对于线性可分的二分类问题，我们的目标是找到一个超平面：

$w^T x + b = 0$

其中 $w$ 是法向量， $b$ 是偏置项。分类间隔定义为最近样本点到超平面的距离的两倍，数学表达式为：

$margin=2∣∣w∣∣\text{margin} = \frac{2}{||w||}$

import numpy as np
import matplotlib.pyplot as plt
from sklearn.svm import SVC
from sklearn.datasets import make_classificationclass LinearSVMVisualizer:"""线性SVM可视化器"""def __init__(self):self.model = Noneself.X = Noneself.y = Nonedef generate_sample_data(self, n_samples=100, n_features=2):"""生成示例数据"""# 生成线性可分的二分类数据self.X, self.y = make_classification(n_samples=n_samples,n_features=n_features,n_redundant=0,n_informative=2,n_clusters_per_class=1,class_sep=2.0,  # 增大类别间距离，确保线性可分random_state=42)return self.X, self.ydef train_svm(self, C=1.0, kernel='linear'):"""训练SVM模型"""self.model = SVC(C=C, kernel=kernel, random_state=42)self.model.fit(self.X, self.y)# 输出关键参数print(f"**支持向量数量**: {len(self.model.support_)}")print(f"**决策函数系数**: {self.model.coef_}")print(f"**截距项**: {self.model.intercept_}")return self.modeldef calculate_margin(self):"""计算分类间隔"""if self.model is None:raise ValueError("模型尚未训练")# 计算权重向量的模长w_norm = np.linalg.norm(self.model.coef_)margin = 2.0 / w_normprint(f"**分类间隔**: {margin:.4f}")return margindef visualize_decision_boundary(self):"""可视化决策边界和支持向量"""if self.X.shape[1] != 2:print("只支持二维数据的可视化")returnplt.figure(figsize=(12, 8))# 创建网格点用于绘制决策边界h = 0.02x_min, x_max = self.X[:, 0].min() - 1, self.X[:, 0].max() + 1y_min, y_max = self.X[:, 1].min() - 1, self.X[:, 1].max() + 1xx, yy = np.meshgrid(np.arange(x_min, x_max, h),np.arange(y_min, y_max, h))# 预测网格点Z = self.model.decision_function(np.c_[xx.ravel(), yy.ravel()])Z = Z.reshape(xx.shape)# 绘制决策边界和间隔plt.contour(xx, yy, Z, levels=[-1, 0, 1], colors=['red', 'black', 'red'],linestyles=['--', '-', '--'],linewidths=[2, 3, 2])# 绘制数据点scatter = plt.scatter(self.X[:, 0], self.X[:, 1], c=self.y, cmap='viridis', s=50, alpha=0.8)# 高亮支持向量support_vectors = self.X[self.model.support_]plt.scatter(support_vectors[:, 0], support_vectors[:, 1],s=200, facecolors='none', edgecolors='red', linewidth=2)plt.title('**SVM决策边界与支持向量可视化**', fontsize=14, fontweight='bold')plt.xlabel('特征1', fontsize=12)plt.ylabel('特征2', fontsize=12)plt.colorbar(scatter)plt.grid(True, alpha=0.3)plt.show()# 使用示例
visualizer = LinearSVMVisualizer()
X, y = visualizer.generate_sample_data()
model = visualizer.train_svm(C=1.0)
margin = visualizer.calculate_margin()
visualizer.visualize_decision_boundary()

关键代码解析：

make_classification函数生成线性可分数据，class_sep参数控制类别间距
decision_function方法返回样本到决策边界的距离
支持向量通过model.support_属性获取，这些是决定决策边界的关键样本点

1.2 优化问题的数学表述

SVM的训练过程本质上是一个约束优化问题。对于线性可分情况，我们需要求解：

$min⁡w,b12∣∣w∣∣2\min_{w,b} \frac{1}{2}||w||^2$

约束条件： $yi(wTxi+b)≥1,i=1,2,...,ny_i(w^T x_i + b) \geq 1, \quad i = 1,2,...,n$

图1：SVM优化问题流程图

2. 软间隔SVM与正则化

2.1 处理线性不可分数据

在实际应用中，数据往往不是完全线性可分的。软间隔SVM通过引入松弛变量 $ξi\xi_i$ 来处理这种情况，允许某些样本点违反间隔约束。

优化目标变为：

$min⁡w,b,ξ12∣∣w∣∣2+C∑i=1nξi\min_{w,b,\xi} \frac{1}{2}||w||^2 + C\sum_{i=1}^n \xi_i$

约束条件：
$yi(wTxi+b)≥1−ξiy_i(w^T x_i + b) \geq 1 - \xi_i$
$ξi≥0\xi_i \geq 0$

其中 $C$ 是正则化参数，控制对误分类的惩罚程度。

import numpy as np
from sklearn.svm import SVC
from sklearn.model_selection import GridSearchCV, cross_val_score
from sklearn.preprocessing import StandardScaler
from sklearn.pipeline import Pipelineclass SoftMarginSVM:"""软间隔SVM实现与参数优化"""def __init__(self):self.pipeline = Noneself.best_params = Noneself.cv_scores = Nonedef create_pipeline(self):"""创建SVM处理管道"""# 标准化 + SVMself.pipeline = Pipeline([('scaler', StandardScaler()),  # 特征标准化('svm', SVC(probability=True, random_state=42))])return self.pipelinedef optimize_hyperparameters(self, X, y, cv=5):"""超参数优化"""# **关键参数网格搜索**param_grid = {'svm__C': [0.01, 0.1, 1, 10, 100],  # 正则化参数'svm__kernel': ['linear', 'rbf', 'poly'],  # 核函数类型'svm__gamma': ['scale', 'auto', 0.001, 0.01, 0.1, 1],  # RBF核参数'svm__degree': [2, 3, 4]  # 多项式核次数}# 网格搜索grid_search = GridSearchCV(self.pipeline, param_grid, cv=cv, scoring='accuracy',n_jobs=-1,verbose=1)grid_search.fit(X, y)self.best_params = grid_search.best_params_self.pipeline = grid_search.best_estimator_print("**最优参数组合**:")for param, value in self.best_params.items():print(f"  {param}: {value}")print(f"**最优交叉验证得分**: {grid_search.best_score_:.4f}")return self.best_paramsdef analyze_regularization_effect(self, X, y, C_values=None):"""分析正则化参数C的影响"""if C_values is None:C_values = [0.01, 0.1, 1, 10, 100, 1000]train_scores = []val_scores = []support_vector_counts = []for C in C_values:# 训练模型svm = SVC(C=C, kernel='rbf', random_state=42)svm.fit(X, y)# 计算训练和验证得分train_score = svm.score(X, y)val_score = np.mean(cross_val_score(svm, X, y, cv=5))train_scores.append(train_score)val_scores.append(val_score)support_vector_counts.append(len(svm.support_))print(f"**C={C}**: 训练得分={train_score:.4f}, "f"验证得分={val_score:.4f}, 支持向量数={len(svm.support_)}")return {'C_values': C_values,'train_scores': train_scores,'val_scores': val_scores,'support_vector_counts': support_vector_counts}def calculate_decision_scores(self, X):"""计算决策函数值"""if self.pipeline is None:raise ValueError("模型尚未训练")# 获取SVM模型svm_model = self.pipeline.named_steps['svm']# 计算到决策边界的距离decision_scores = svm_model.decision_function(X)# 分析支持向量support_vectors_idx = svm_model.support_support_vectors = X[support_vectors_idx]print(f"**支持向量数量**: {len(support_vectors_idx)}")print(f"**支持向量占比**: {len(support_vectors_idx)/len(X)*100:.2f}%")return {'decision_scores': decision_scores,'support_vectors_idx': support_vectors_idx,'support_vectors': support_vectors}# 使用示例
from sklearn.datasets import make_classification# 生成带噪声的数据（线性不可分）
X, y = make_classification(n_samples=200, n_features=2, n_redundant=0,n_informative=2, n_clusters_per_class=1,class_sep=1.0, flip_y=0.1, random_state=42)soft_svm = SoftMarginSVM()
pipeline = soft_svm.create_pipeline()# 超参数优化
best_params = soft_svm.optimize_hyperparameters(X, y)# 正则化效应分析
reg_analysis = soft_svm.analyze_regularization_effect(X, y)

关键参数说明：

C参数：控制对误分类的容忍度，C越大越严格，C越小越宽松
gamma参数：RBF核的带宽参数，影响决策边界的复杂度
支持向量数量：反映模型复杂度，数量越少模型越简单

3. 核函数与非线性SVM

3.1 核技巧的数学原理

核技巧（Kernel Trick）是SVM处理非线性问题的核心技术。它通过隐式地将数据映射到高维特征空间，使得原本线性不可分的数据在新空间中变得线性可分。

常用核函数包括：

线性核： $K(x_i, x_j) = x_i^T x_j$
多项式核： $K(xi,xj)=(γxiTxj+r)dK(x_i, x_j) = (\gamma x_i^T x_j + r)^d$
RBF核： $K(xi,xj)=exp⁡(−γ∣∣xi−xj∣∣2)K(x_i, x_j) = \exp(-\gamma ||x_i - x_j||^2)$
Sigmoid核： $K(xi,xj)=tanh⁡(γxiTxj+r)K(x_i, x_j) = \tanh(\gamma x_i^T x_j + r)$

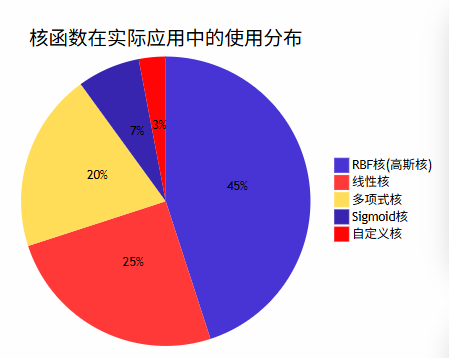
图2：核函数类型对比图
在这里插入图片描述

import numpy as np
from sklearn.svm import SVC
from sklearn.datasets import make_circles, make_moons
import matplotlib.pyplot as pltclass KernelSVMComparison:"""核函数SVM对比分析"""def __init__(self):self.kernels = {'linear': {'name': '线性核', 'params': {}},'poly': {'name': '多项式核', 'params': {'degree': 3}},'rbf': {'name': 'RBF核', 'params': {'gamma': 'scale'}},'sigmoid': {'name': 'Sigmoid核', 'params': {'gamma': 'scale'}}}self.models = {}self.datasets = {}def generate_nonlinear_datasets(self):"""生成非线性数据集"""# **同心圆数据集**X_circles, y_circles = make_circles(n_samples=200, noise=0.1, factor=0.3, random_state=42)# **月牙形数据集**X_moons, y_moons = make_moons(n_samples=200, noise=0.1, random_state=42)# **异或问题数据集**np.random.seed(42)X_xor = np.random.randn(200, 2)y_xor = np.logical_xor(X_xor[:, 0] > 0, X_xor[:, 1] > 0).astype(int)self.datasets = {'circles': (X_circles, y_circles, '同心圆'),'moons': (X_moons, y_moons, '月牙形'),'xor': (X_xor, y_xor, '异或问题')}return self.datasetsdef train_all_kernels(self, X, y, C=1.0):"""使用不同核函数训练SVM"""results = {}for kernel_name, kernel_info in self.kernels.items():print(f"\n**训练{kernel_info['name']}SVM**...")# 创建并训练模型svm = SVC(C=C, kernel=kernel_name, probability=True, random_state=42,**kernel_info['params'])svm.fit(X, y)# 计算性能指标train_accuracy = svm.score(X, y)support_vector_count = len(svm.support_)results[kernel_name] = {'model': svm,'accuracy': train_accuracy,'support_vectors': support_vector_count,'kernel_name': kernel_info['name']}print(f"  训练准确率: {train_accuracy:.4f}")print(f"  支持向量数: {support_vector_count}")return resultsdef analyze_rbf_gamma_effect(self, X, y, gamma_values=None):"""分析RBF核中gamma参数的影响"""if gamma_values is None:gamma_values = [0.001, 0.01, 0.1, 1, 10, 100]results = []print("\n**RBF核gamma参数影响分析**:")print("gamma值 | 训练准确率 | 支持向量数 | 决策边界复杂度")print("-" * 50)for gamma in gamma_values:svm = SVC(kernel='rbf', gamma=gamma, C=1.0, random_state=42)svm.fit(X, y)accuracy = svm.score(X, y)sv_count = len(svm.support_)# 计算决策边界复杂度（通过支持向量占比估算）complexity = sv_count / len(X)results.append({'gamma': gamma,'accuracy': accuracy,'support_vectors': sv_count,'complexity': complexity})print(f"{gamma:6.3f} | {accuracy:10.4f} | {sv_count:11d} | {complexity:13.4f}")return resultsdef visualize_kernel_comparison(self, dataset_name='circles'):"""可视化不同核函数的效果"""if dataset_name not in self.datasets:print(f"数据集 {dataset_name} 不存在")returnX, y, title = self.datasets[dataset_name]results = self.train_all_kernels(X, y)fig, axes = plt.subplots(2, 2, figsize=(15, 12))axes = axes.ravel()for idx, (kernel_name, result) in enumerate(results.items()):ax = axes[idx]model = result['model']# 创建网格h = 0.02x_min, x_max = X[:, 0].min() - 0.5, X[:, 0].max() + 0.5y_min, y_max = X[:, 1].min() - 0.5, X[:, 1].max() + 0.5xx, yy = np.meshgrid(np.arange(x_min, x_max, h),np.arange(y_min, y_max, h))# 预测Z = model.predict(np.c_[xx.ravel(), yy.ravel()])Z = Z.reshape(xx.shape)# 绘制决策边界ax.contourf(xx, yy, Z, alpha=0.3, cmap='viridis')# 绘制数据点scatter = ax.scatter(X[:, 0], X[:, 1], c=y, cmap='viridis', s=50, edgecolors='black', alpha=0.8)# 高亮支持向量support_vectors = X[model.support_]ax.scatter(support_vectors[:, 0], support_vectors[:, 1],s=200, facecolors='none', edgecolors='red', linewidth=2)ax.set_title(f"**{result['kernel_name']}**\n"f"准确率: {result['accuracy']:.3f}, "f"支持向量: {result['support_vectors']}", fontweight='bold')ax.set_xlabel('特征1')ax.set_ylabel('特征2')plt.suptitle(f'**不同核函数在{title}数据集上的表现**', fontsize=16, fontweight='bold')plt.tight_layout()plt.show()# 使用示例
kernel_comparison = KernelSVMComparison()
datasets = kernel_comparison.generate_nonlinear_datasets()# 对每个数据集进行核函数对比
for dataset_name in ['circles', 'moons', 'xor']:print(f"\n{'='*50}")print(f"**{datasets[dataset_name][2]}数据集分析**")print(f"{'='*50}")X, y, _ = datasets[dataset_name]# 训练不同核函数results = kernel_comparison.train_all_kernels(X, y)# RBF核gamma参数分析if dataset_name == 'circles':  # 只对一个数据集做详细分析gamma_analysis = kernel_comparison.analyze_rbf_gamma_effect(X, y)# 可视化kernel_comparison.visualize_kernel_comparison(dataset_name)

核函数选择指南：

线性核：适用于线性可分或高维稀疏数据
RBF核：通用性最强，适用于大多数非线性问题
多项式核：适用于图像处理等需要考虑特征交互的场景
Sigmoid核：类似神经网络，但实际应用较少

4. SVM参数优化与性能调优

4.1 关键参数详解

SVM的性能很大程度上取决于参数的选择。主要参数包括正则化参数C、核函数参数gamma、以及核函数类型的选择。

参数	作用	取值范围	调优策略	影响
C	正则化强度	0.01-1000	网格搜索	控制过拟合程度
gamma	RBF核带宽	0.001-100	对数搜索	决策边界复杂度
kernel	核函数类型	linear/rbf/poly	交叉验证	模型表达能力
degree	多项式核次数	2-5	逐步增加	特征交互复杂度
class_weight	类别权重	balanced/dict	样本不平衡时调整	处理不平衡数据

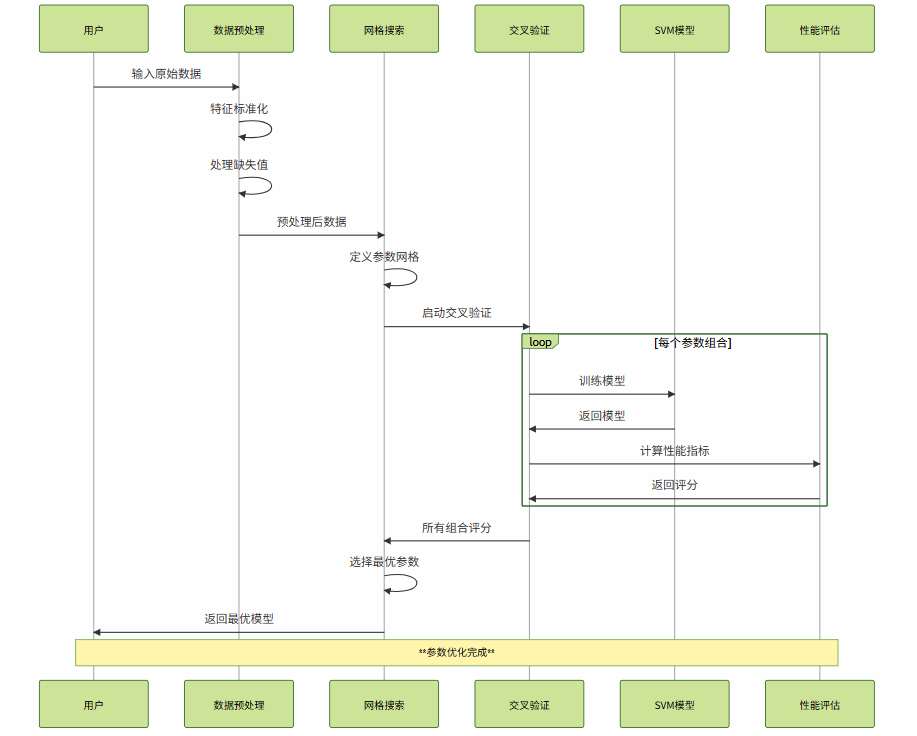
图3：SVM参数优化流程时序图
在这里插入图片描述

import numpy as np
from sklearn.svm import SVC
from sklearn.model_selection import (GridSearchCV, RandomizedSearchCV, cross_val_score, learning_curve)
from sklearn.preprocessing import StandardScaler
from sklearn.metrics import classification_report, confusion_matrix
from sklearn.pipeline import Pipeline
import matplotlib.pyplot as plt
from scipy.stats import uniform, loguniformclass SVMOptimizer:"""SVM参数优化器"""def __init__(self):self.best_model = Noneself.optimization_history = []self.performance_metrics = {}def grid_search_optimization(self, X, y, cv=5, scoring='accuracy'):"""网格搜索参数优化"""print("**开始网格搜索优化**...")# 创建管道pipeline = Pipeline([('scaler', StandardScaler()),('svm', SVC(random_state=42, probability=True))])# **精细化参数网格**param_grid = [{'svm__kernel': ['linear'],'svm__C': [0.01, 0.1, 1, 10, 100]},{'svm__kernel': ['rbf'],'svm__C': [0.01, 0.1, 1, 10, 100],'svm__gamma': ['scale', 'auto', 0.001, 0.01, 0.1, 1]},{'svm__kernel': ['poly'],'svm__C': [0.1, 1, 10],'svm__degree': [2, 3, 4],'svm__gamma': ['scale', 'auto']}]# 执行网格搜索grid_search = GridSearchCV(pipeline, param_grid, cv=cv, scoring=scoring,n_jobs=-1, verbose=1, return_train_score=True)grid_search.fit(X, y)self.best_model = grid_search.best_estimator_# 记录优化结果optimization_result = {'method': 'grid_search','best_params': grid_search.best_params_,'best_score': grid_search.best_score_,'cv_results': grid_search.cv_results_}self.optimization_history.append(optimization_result)print(f"**最优参数**: {grid_search.best_params_}")print(f"**最优得分**: {grid_search.best_score_:.4f}")return grid_searchdef random_search_optimization(self, X, y, n_iter=100, cv=5):"""随机搜索参数优化"""print("**开始随机搜索优化**...")pipeline = Pipeline([('scaler', StandardScaler()),('svm', SVC(random_state=42, probability=True))])# **随机参数分布**param_distributions = {'svm__kernel': ['linear', 'rbf', 'poly'],'svm__C': loguniform(0.01, 100),  # 对数均匀分布'svm__gamma': loguniform(0.001, 1),'svm__degree': [2, 3, 4, 5]}# 执行随机搜索random_search = RandomizedSearchCV(pipeline, param_distributions, n_iter=n_iter,cv=cv, scoring='accuracy', n_jobs=-1, verbose=1, random_state=42)random_search.fit(X, y)print(f"**随机搜索最优参数**: {random_search.best_params_}")print(f"**随机搜索最优得分**: {random_search.best_score_:.4f}")return random_searchdef analyze_learning_curves(self, X, y, train_sizes=None):"""分析学习曲线"""if self.best_model is None:print("请先进行参数优化")returnif train_sizes is None:train_sizes = np.linspace(0.1, 1.0, 10)print("**生成学习曲线**...")# 计算学习曲线train_sizes, train_scores, val_scores = learning_curve(self.best_model, X, y, train_sizes=train_sizes,cv=5, n_jobs=-1, random_state=42)# 计算均值和标准差train_mean = np.mean(train_scores, axis=1)train_std = np.std(train_scores, axis=1)val_mean = np.mean(val_scores, axis=1)val_std = np.std(val_scores, axis=1)# 绘制学习曲线plt.figure(figsize=(10, 6))plt.plot(train_sizes, train_mean, 'o-', color='blue', label='训练得分', linewidth=2)plt.fill_between(train_sizes, train_mean - train_std,train_mean + train_std, alpha=0.1, color='blue')plt.plot(train_sizes, val_mean, 'o-', color='red',label='验证得分', linewidth=2)plt.fill_between(train_sizes, val_mean - val_std,val_mean + val_std, alpha=0.1, color='red')plt.xlabel('训练样本数量')plt.ylabel('准确率')plt.title('**SVM学习曲线分析**', fontweight='bold')plt.legend()plt.grid(True, alpha=0.3)plt.show()# 分析结果final_gap = train_mean[-1] - val_mean[-1]print(f"**最终训练-验证差距**: {final_gap:.4f}")if final_gap > 0.1:print("**建议**: 模型可能过拟合，考虑增加正则化或减少模型复杂度")elif val_mean[-1] < 0.8:print("**建议**: 模型欠拟合，考虑增加模型复杂度或特征工程")else:print("**结论**: 模型性能良好，训练充分")return train_sizes, train_scores, val_scoresdef comprehensive_evaluation(self, X_test, y_test):"""综合性能评估"""if self.best_model is None:print("请先进行参数优化")returnprint("**开始综合性能评估**...")# 预测y_pred = self.best_model.predict(X_test)y_proba = self.best_model.predict_proba(X_test)# 基本指标accuracy = self.best_model.score(X_test, y_test)# 详细报告report = classification_report(y_test, y_pred, output_dict=True)cm = confusion_matrix(y_test, y_pred)# 支持向量分析svm_model = self.best_model.named_steps['svm']support_vector_count = len(svm_model.support_)support_vector_ratio = support_vector_count / len(X_test)self.performance_metrics = {'accuracy': accuracy,'classification_report': report,'confusion_matrix': cm,'support_vector_count': support_vector_count,'support_vector_ratio': support_vector_ratio}print(f"**测试准确率**: {accuracy:.4f}")print(f"**支持向量数量**: {support_vector_count}")print(f"**支持向量占比**: {support_vector_ratio:.4f}")print("\n**分类报告**:")print(classification_report(y_test, y_pred))return self.performance_metrics# 使用示例
from sklearn.datasets import load_breast_cancer
from sklearn.model_selection import train_test_split# 加载数据
data = load_breast_cancer()
X, y = data.data, data.target# 划分数据集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42, stratify=y
)# 创建优化器
optimizer = SVMOptimizer()# 网格搜索优化
grid_result = optimizer.grid_search_optimization(X_train, y_train)# 随机搜索对比
random_result = optimizer.random_search_optimization(X_train, y_train, n_iter=50)# 学习曲线分析
learning_curves = optimizer.analyze_learning_curves(X_train, y_train)# 综合评估
performance = optimizer.comprehensive_evaluation(X_test, y_test)

参数调优最佳实践：

先粗后细：先用较大步长找到大致范围，再精细搜索
交叉验证：使用k折交叉验证避免过拟合
计算资源平衡：网格搜索精确但耗时，随机搜索效率更高
领域知识：结合具体问题特点选择合适的核函数

5. SVM在实际项目中的应用案例

5.2 文本分类实战

文本分类是SVM的经典应用场景之一，特别是在高维稀疏特征空间中，SVM表现出色。

import numpy as np
import pandas as pd
from sklearn.feature_extraction.text import TfidfVectorizer
from sklearn.svm import SVC
from sklearn.pipeline import Pipeline
from sklearn.model_selection import train_test_split, cross_val_score
from sklearn.metrics import classification_report, accuracy_score
import re
import jieba
from collections import Counterclass TextClassificationSVM:"""基于SVM的文本分类系统"""def __init__(self):self.pipeline = Noneself.vectorizer = Noneself.classifier = Noneself.feature_names = Nonedef preprocess_text(self, texts):"""文本预处理"""processed_texts = []for text in texts:# **去除特殊字符和数字**text = re.sub(r'[^\u4e00-\u9fa5a-zA-Z\s]', '', text)# **中文分词**words = jieba.cut(text)# **去除停用词和短词**filtered_words = [word for word in words if len(word) > 1 and word not in self.get_stopwords()]processed_texts.append(' '.join(filtered_words))return processed_textsdef get_stopwords(self):"""获取停用词列表"""# 简化的中文停用词stopwords = {'的', '了', '在', '是', '我', '有', '和', '就', '不', '人','都', '一', '一个', '上', '也', '很', '到', '说', '要', '去','你', '会', '着', '没有', '看', '好', '自己', '这'}return stopwordsdef build_pipeline(self, max_features=10000, ngram_range=(1, 2)):"""构建文本分类管道"""# **TF-IDF特征提取**self.vectorizer = TfidfVectorizer(max_features=max_features,ngram_range=ngram_range,  # 使用1-gram和2-grammin_df=2,  # 最小文档频率max_df=0.95,  # 最大文档频率sublinear_tf=True,  # 使用对数TFnorm='l2'  # L2归一化)# **SVM分类器**self.classifier = SVC(kernel='linear',  # 线性核适合高维稀疏数据C=1.0,probability=True,  # 启用概率预测random_state=42)# **构建管道**self.pipeline = Pipeline([('vectorizer', self.vectorizer),('classifier', self.classifier)])return self.pipelinedef train(self, texts, labels):"""训练模型"""print("**开始文本预处理**...")processed_texts = self.preprocess_text(texts)print("**开始模型训练**...")self.pipeline.fit(processed_texts, labels)# 获取特征名称self.feature_names = self.vectorizer.get_feature_names_out()print(f"**特征维度**: {len(self.feature_names)}")print(f"**支持向量数**: {len(self.classifier.support_)}")return self.pipelinedef predict(self, texts, return_proba=False):"""预测文本类别"""processed_texts = self.preprocess_text(texts)if return_proba:return self.pipeline.predict_proba(processed_texts)else:return self.pipeline.predict(processed_texts)def analyze_feature_importance(self, class_names, top_n=20):"""分析特征重要性"""if self.classifier.coef_ is None:print("模型尚未训练或不支持特征重要性分析")return# 获取特征权重coef = self.classifier.coef_[0]  # 二分类情况# 获取最重要的正向和负向特征top_positive_idx = np.argsort(coef)[-top_n:][::-1]top_negative_idx = np.argsort(coef)[:top_n]print(f"**{class_names[1]}类别的重要特征** (正向权重):")for idx in top_positive_idx:print(f"  {self.feature_names[idx]}: {coef[idx]:.4f}")print(f"\n**{class_names[0]}类别的重要特征** (负向权重):")for idx in top_negative_idx:print(f"  {self.feature_names[idx]}: {coef[idx]:.4f}")return {'positive_features': [(self.feature_names[idx], coef[idx]) for idx in top_positive_idx],'negative_features': [(self.feature_names[idx], coef[idx]) for idx in top_negative_idx]}def evaluate_model(self, test_texts, test_labels, class_names):"""模型评估"""predictions = self.predict(test_texts)probabilities = self.predict(test_texts, return_proba=True)# 基本指标accuracy = accuracy_score(test_labels, predictions)print(f"**测试准确率**: {accuracy:.4f}")print("\n**详细分类报告**:")print(classification_report(test_labels, predictions, target_names=class_names))# 置信度分析confidence_scores = np.max(probabilities, axis=1)print(f"\n**平均预测置信度**: {np.mean(confidence_scores):.4f}")print(f"**置信度标准差**: {np.std(confidence_scores):.4f}")return {'accuracy': accuracy,'predictions': predictions,'probabilities': probabilities,'confidence_scores': confidence_scores}# 使用示例（模拟数据）
def generate_sample_text_data():"""生成示例文本数据"""positive_texts = ["这个产品质量很好，非常满意，值得推荐给朋友","服务态度优秀，解决问题及时，体验很棒","功能强大，界面友好，使用起来很方便","性价比高，物超所值，下次还会购买","快递速度快，包装完好，商品质量不错"] * 20  # 重复生成更多数据negative_texts = ["产品质量差，用了几天就坏了，很失望","客服态度恶劣，问题得不到解决，体验糟糕","功能有限，操作复杂，不推荐购买","价格虚高，质量一般，不值这个价钱","发货慢，包装破损，商品有瑕疵"] * 20texts = positive_texts + negative_textslabels = [1] * len(positive_texts) + [0] * len(negative_texts)return texts, labels# 实际使用
texts, labels = generate_sample_text_data()
class_names = ['负面', '正面']# 划分数据集
X_train, X_test, y_train, y_test = train_test_split(texts, labels, test_size=0.2, random_state=42, stratify=labels
)# 创建分类器
text_classifier = TextClassificationSVM()# 构建管道
pipeline = text_classifier.build_pipeline(max_features=5000)# 训练模型
text_classifier.train(X_train, y_train)# 特征重要性分析
feature_importance = text_classifier.analyze_feature_importance(class_names)# 模型评估
evaluation_results = text_classifier.evaluate_model(X_test, y_test, class_names)# 新文本预测示例
new_texts = ["这个产品真的很棒，强烈推荐", "质量太差了，完全不能用"]
predictions = text_classifier.predict(new_texts, return_proba=True)print("\n**新文本预测结果**:")
for i, text in enumerate(new_texts):prob_neg, prob_pos = predictions[i]predicted_class = class_names[1] if prob_pos > prob_neg else class_names[0]confidence = max(prob_pos, prob_neg)print(f"文本: {text}")print(f"预测类别: {predicted_class} (置信度: {confidence:.4f})")print()

文本分类关键技术点：

特征工程：TF-IDF向量化，n-gram特征，停用词过滤
核函数选择：线性核适合高维稀疏文本特征
正则化调优：防止在高维空间中过拟合
特征选择：通过权重分析理解模型决策依据

6. SVM性能分析与可视化

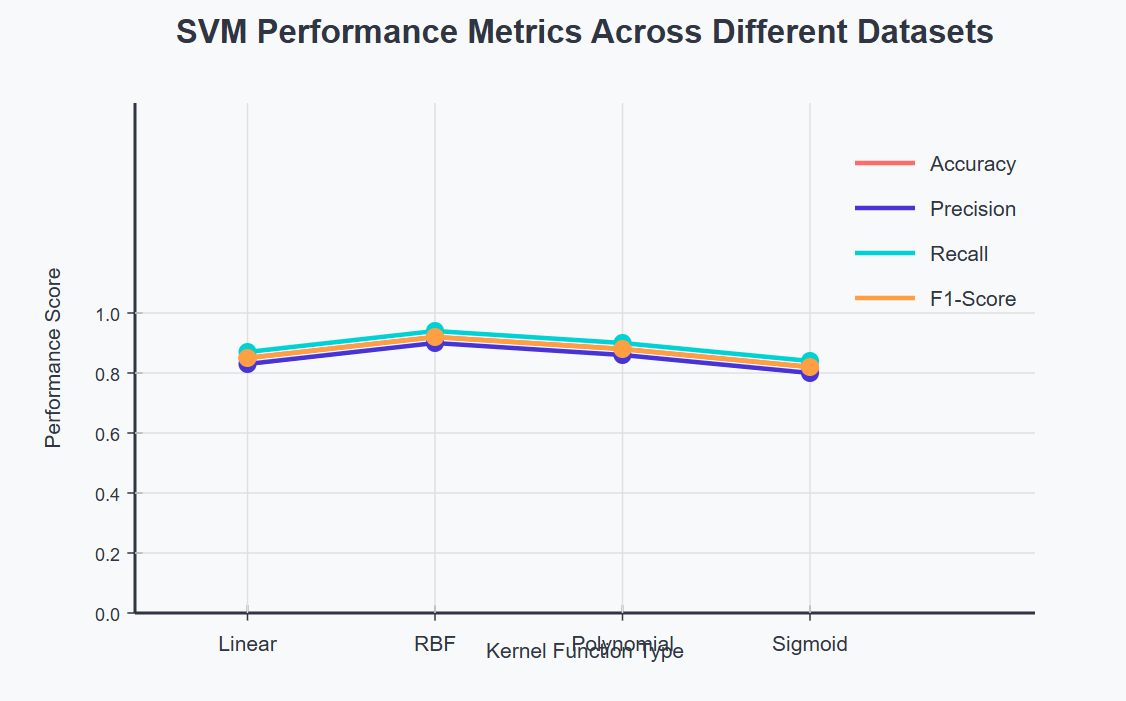
图4：SVM性能指标趋势分析
在这里插入图片描述

6.1 模型解释性分析

SVM的一个重要优势是其良好的可解释性，特别是线性SVM，我们可以直接分析特征权重来理解模型的决策过程。

“支持向量机的美妙之处在于它不仅给出了预测结果，更重要的是告诉我们哪些样本是关键的决策边界点。这些支持向量承载着数据中最重要的信息，是模型泛化能力的基石。” —— 统计学习理论经典观点

import numpy as np
import matplotlib.pyplot as plt
from sklearn.svm import SVC
from sklearn.datasets import make_classification
from sklearn.preprocessing import StandardScaler
import seaborn as snsclass SVMInterpretability:"""SVM模型解释性分析"""def __init__(self):self.model = Noneself.scaler = Noneself.feature_importance = Nonedef train_interpretable_svm(self, X, y, kernel='linear', C=1.0):"""训练可解释的SVM模型"""# 特征标准化self.scaler = StandardScaler()X_scaled = self.scaler.fit_transform(X)# 训练模型self.model = SVC(kernel=kernel, C=C, random_state=42)self.model.fit(X_scaled, y)print(f"**模型训练完成**")print(f"支持向量数量: {len(self.model.support_)}")print(f"支持向量占比: {len(self.model.support_)/len(X)*100:.2f}%")return self.modeldef analyze_feature_importance(self, feature_names=None):"""分析特征重要性"""if self.model.kernel != 'linear':print("**注意**: 非线性核函数的特征重要性分析较为复杂")return None# 获取特征权重weights = self.model.coef_[0]if feature_names is None:feature_names = [f'Feature_{i}' for i in range(len(weights))]# 计算特征重要性（绝对值）importance = np.abs(weights)# 排序sorted_idx = np.argsort(importance)[::-1]self.feature_importance = {'weights': weights,'importance': importance,'sorted_idx': sorted_idx,'feature_names': feature_names}print("**特征重要性排序** (前10个):")for i in range(min(10, len(sorted_idx))):idx = sorted_idx[i]print(f"{i+1:2d}. {feature_names[idx]:15s}: "f"权重={weights[idx]:8.4f}, 重要性={importance[idx]:.4f}")return self.feature_importancedef visualize_support_vectors(self, X, y, feature_idx=(0, 1)):"""可视化支持向量"""if X.shape[1] < 2:print("需要至少2个特征进行可视化")returnX_scaled = self.scaler.transform(X)plt.figure(figsize=(12, 8))# 绘制所有数据点colors = ['red', 'blue']for class_val in np.unique(y):mask = y == class_valplt.scatter(X_scaled[mask, feature_idx[0]], X_scaled[mask, feature_idx[1]],c=colors[class_val], alpha=0.6, s=50,label=f'Class {class_val}')# 高亮支持向量support_vectors = X_scaled[self.model.support_]plt.scatter(support_vectors[:, feature_idx[0]], support_vectors[:, feature_idx[1]],s=200, facecolors='none', edgecolors='black', linewidth=3, label='Support Vectors')# 绘制决策边界（仅适用于2D情况）if self.model.kernel == 'linear' and len(feature_idx) == 2:self._plot_decision_boundary(X_scaled, feature_idx)plt.xlabel(f'Feature {feature_idx[0]}')plt.ylabel(f'Feature {feature_idx[1]}')plt.title('**SVM支持向量可视化**', fontweight='bold')plt.legend()plt.grid(True, alpha=0.3)plt.show()def _plot_decision_boundary(self, X, feature_idx):"""绘制决策边界"""# 创建网格h = 0.02x_min, x_max = X[:, feature_idx[0]].min() - 1, X[:, feature_idx[0]].max() + 1y_min, y_max = X[:, feature_idx[1]].min() - 1, X[:, feature_idx[1]].max() + 1xx, yy = np.meshgrid(np.arange(x_min, x_max, h),np.arange(y_min, y_max, h))# 创建完整特征向量（其他特征设为0）grid_points = np.zeros((xx.ravel().shape[0], X.shape[1]))grid_points[:, feature_idx[0]] = xx.ravel()grid_points[:, feature_idx[1]] = yy.ravel()# 预测Z = self.model.decision_function(grid_points)Z = Z.reshape(xx.shape)# 绘制等高线plt.contour(xx, yy, Z, levels=[-1, 0, 1], colors=['red', 'black', 'red'],linestyles=['--', '-', '--'], linewidths=[2, 3, 2])def analyze_decision_confidence(self, X, y):"""分析决策置信度"""X_scaled = self.scaler.transform(X)# 计算决策函数值decision_scores = self.model.decision_function(X_scaled)# 分析置信度分布confidence_stats = {'mean': np.mean(np.abs(decision_scores)),'std': np.std(np.abs(decision_scores)),'min': np.min(np.abs(decision_scores)),'max': np.max(np.abs(decision_scores))}print("**决策置信度统计**:")print(f"平均置信度: {confidence_stats['mean']:.4f}")print(f"置信度标准差: {confidence_stats['std']:.4f}")print(f"最小置信度: {confidence_stats['min']:.4f}")print(f"最大置信度: {confidence_stats['max']:.4f}")# 可视化置信度分布plt.figure(figsize=(12, 5))plt.subplot(1, 2, 1)plt.hist(decision_scores, bins=30, alpha=0.7, edgecolor='black')plt.axvline(x=0, color='red', linestyle='--', linewidth=2)plt.xlabel('决策函数值')plt.ylabel('频次')plt.title('**决策函数值分布**', fontweight='bold')plt.grid(True, alpha=0.3)plt.subplot(1, 2, 2)for class_val in np.unique(y):mask = y == class_valplt.hist(decision_scores[mask], bins=20, alpha=0.7, label=f'Class {class_val}', edgecolor='black')plt.axvline(x=0, color='red', linestyle='--', linewidth=2)plt.xlabel('决策函数值')plt.ylabel('频次')plt.title('**各类别决策函数值分布**', fontweight='bold')plt.legend()plt.grid(True, alpha=0.3)plt.tight_layout()plt.show()return confidence_stats, decision_scores# 使用示例
# 生成示例数据
X, y = make_classification(n_samples=200, n_features=4, n_redundant=0,n_informative=4, n_clusters_per_class=1,class_sep=1.5, random_state=42)feature_names = ['Feature_A', 'Feature_B', 'Feature_C', 'Feature_D']# 创建解释性分析器
interpreter = SVMInterpretability()# 训练模型
model = interpreter.train_interpretable_svm(X, y, kernel='linear', C=1.0)# 特征重要性分析
importance = interpreter.analyze_feature_importance(feature_names)# 支持向量可视化
interpreter.visualize_support_vectors(X, y, feature_idx=(0, 1))# 决策置信度分析
confidence_stats, decision_scores = interpreter.analyze_decision_confidence(X, y)

模型解释性要点：

线性核权重：直接反映特征对分类的贡献
支持向量：决定决策边界的关键样本
决策函数值：样本到决策边界的距离，反映分类置信度
间隔分析：间隔大小反映模型的泛化能力

7. SVM实践总结与未来展望

作为一名在机器学习领域深耕多年的技术实践者，我深深感受到支持向量机这一经典算法的持久魅力和实用价值。SVM不仅仅是一个分类工具，更是统计学习理论与实际应用完美结合的典范。从最初的线性分类到核技巧的引入，从硬间隔到软间隔的演进，SVM的每一次发展都体现了机器学习理论的深度和优雅。

在我的项目实践中，SVM展现出了令人印象深刻的稳定性和可靠性。无论是在高维文本分类、图像识别，还是在生物信息学和金融风控等领域，SVM都能够提供robust的解决方案。其最大间隔的思想不仅保证了良好的泛化性能，更体现了奥卡姆剃刀原理在机器学习中的深刻应用。

SVM的核心优势在于其坚实的数学基础和优秀的泛化能力。通过拉格朗日对偶理论，我们将复杂的约束优化问题转化为凸优化问题，保证了全局最优解的存在。核技巧的引入更是让SVM能够处理复杂的非线性问题，这种数学上的优雅转换至今仍让我感到由衷的敬佩。

展望未来，虽然深度学习在许多领域取得了突破性进展，但SVM在某些特定场景下仍具有不可替代的优势。在小样本学习、高维稀疏数据处理、以及需要模型解释性的应用中，SVM依然是首选方案。随着量子计算和边缘计算的发展，我相信SVM会在新的计算范式下焕发新的活力。

对于想要深入掌握SVM的技术同仁，我建议从数学原理入手，深入理解优化理论和核方法的本质，然后通过大量的实践项目来积累经验。记住，算法的价值不在于其复杂程度，而在于其解决实际问题的能力和理论的优雅性。在这个AI技术日新月异的时代，让我们继续在机器学习的道路上探索前行，用扎实的理论基础和丰富的实践经验，为技术进步贡献自己的力量。

■ 我是蒋星熠Jaxonic！如果这篇文章在你的技术成长路上留下了印记

■ 👁 【关注】与我一起探索技术的无限可能，见证每一次突破

■ 👍 【点赞】为优质技术内容点亮明灯，传递知识的力量

■ 🔖 【收藏】将精华内容珍藏，随时回顾技术要点

■ 💬 【评论】分享你的独特见解，让思维碰撞出智慧火花

■ 🗳 【投票】用你的选择为技术社区贡献一份力量

■ 技术路漫漫，让我们携手前行，在代码的世界里摘取属于程序员的那片星辰大海！