南京大学 - 复杂结构数据挖掘（一）

目录

1. 数据挖掘的目标&作用

2. 应用案例

3. 可被挖掘的数据类型

4. 描述性数据挖掘 + 预测性数据挖掘

5. Attribute types属性类型

6. 隐私保护 -> 汇聚数据

7. 图像展示数据

8. Similarity 相似性分析 - 距离度量

9. 高质量数据

10. Data Cleaning 数据清洗

---

1. 数据挖掘的目标&作用

        具体分析问题前首先要充分了解数据的特征，再针对性地选择合适的建模方式与算法。例如，数据的分布情况、数据的维度、数据的噪声情况等，都会影响到建模与算法的选择。

        大数据、信息爆炸时代，需要在有限的时间内，迅速榨取数据中的有效信息。

        期望：从真实世界中的数据 收集+数据挖掘后的结果 可以适用于真实世界

        数据挖掘（DM，Data Mining）是数据库知识发现（KDD，Knowledge Discovery in Databases）的重要部分。KDD 是一个更广泛的过程，它包括从数据选择、预处理、数据挖掘到模式评估和知识表示等一系列步骤，而数据挖掘专注于从数据中发现模式这一核心环节。​

2. 应用案例

1. 零售：沃尔玛分析交易数据，发现啤酒和尿布常被一起购买，源于美国年轻父亲购物习惯。基于此，将二者并排摆放，提升了销量。​
2. 营销：企业借助数据挖掘分析用户信息、浏览及消费行为，定位潜在购买用户，开展精准营销，如推送专属优惠。​
3. 生物医学：科研人员挖掘基因序列，对比患者与健康人群基因，寻找疾病相关基因片段，助力疾病诊断与新药研发。​
4. 医疗诊断：整合患者影像、检验、病历等多源数据，运用数据挖掘辅助医生识别病变，提高诊断准确性。​
5. 金融投资：通过分析金融交易数据，利用时间序列、机器学习等方法预测股价走势，辅助投资者决策，金融机构也借此评估风险。​
6. 智能交通：自动驾驶汽车传感器数据经数据挖掘技术处理，识别道路环境，做出行驶决策，保障安全。​
7. 文物鉴定：收集文物材质、工艺等特征数据，构建模型鉴别真伪，促进文物市场健康发展。​
8. 政治竞选：竞选团队挖掘选民分布、支持率数据，选择合适演讲地点，提高候选人影响力 。

3. 可被挖掘的数据类型

1. 表格数据：每一行代表一个记录，每一列代表一个属性。例如常见的数据库表、Excel 表格数据等；结构清晰，便于进行传统的数据挖掘算法操作。​
2. 数据仓库（data warehouse）：是一个面向主题的、集成的、相对稳定的、反映历史变化的数据集合，用于支持管理决策。它整合了企业内多个数据源的数据，经过清洗、转换等处理后存储起来，为数据挖掘提供了丰富的数据资源，以支持企业的战略决策制定。​
3. 文本数据（text data）：如论文、pdf 文档、网页文本等。这类数据挖掘的难点在于分词和断句，因为自然语言具有复杂性和灵活性。不同的语言有不同的语法规则和表达方式，即使是同一种语言，也存在多种表达方式和语义歧义。需要通过自然语言处理NLP技术，将文本数据转化为适合挖掘的形式，例如提取关键词、构建文本向量等，进而挖掘文本中的主题、情感倾向、语义关系等信息。​
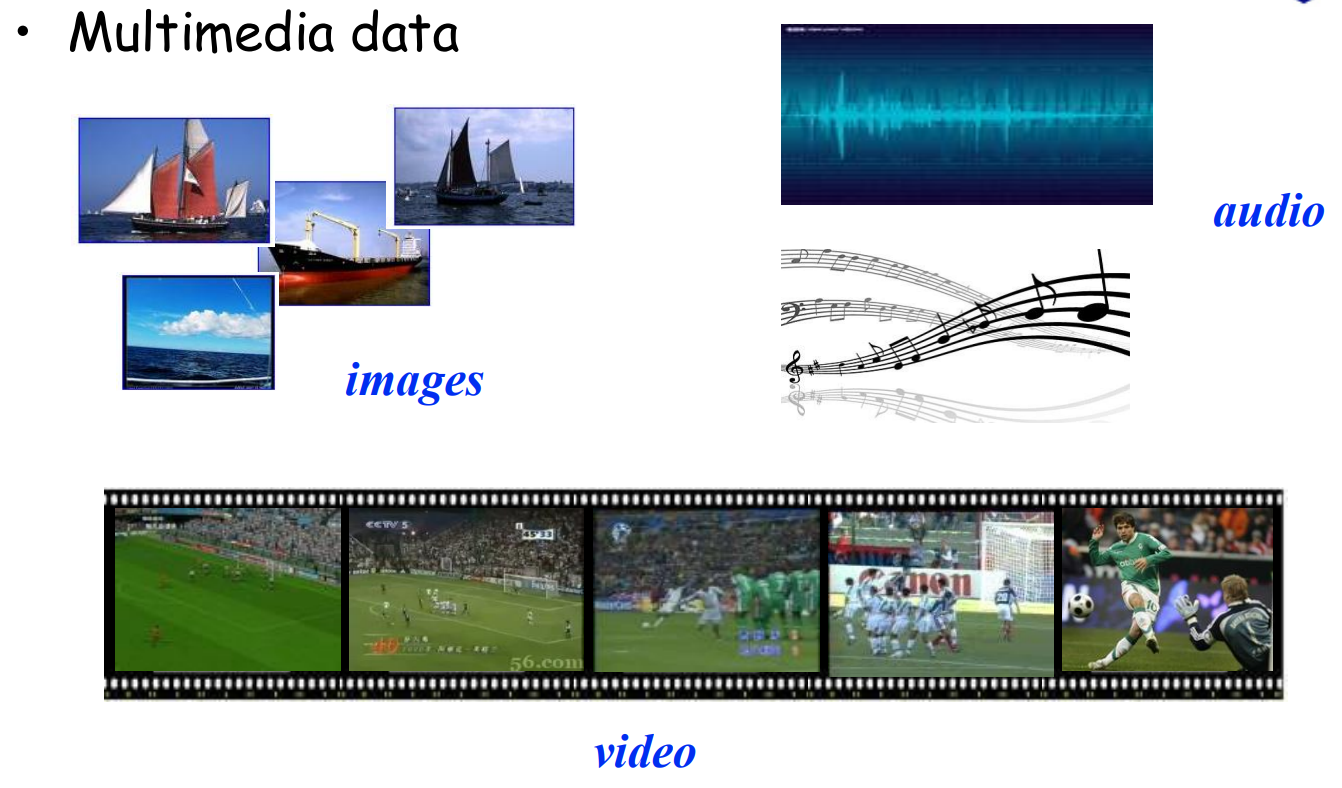
4. 多模态数据：包括音频、图像、视频等。
   1. 例如在图像数据挖掘中，可以识别图像中的物体、进行图像分类、目标检测等；
   2. 音频数据挖掘可以用于语音识别、音乐分类、情感分析等；
   3. 视频数据挖掘则可以结合图像和音频信息，进行视频内容分析、行为识别等。
   4. 由于多模态数据的复杂性，需要综合运用多种技术，如计算机视觉、语音识别、信号处理等，来挖掘其中有价值的信息。​

1. Web 数据：即互联网数据，在挖掘时还要考虑网页的安排结构。网页包含了各种类型的数据，如文本、图片、链接等，且其结构复杂多样。不同网站的页面布局、数据组织方式各不相同，需要通过网页爬虫技术获取数据，并对网页结构进行解析，提取出有用的数据进行挖掘。例如，可以通过挖掘网页链接关系，分析网站的影响力和用户浏览行为；通过分析网页文本内容，了解网站主题和用户需求等。​
2. 社交媒体数据：个体与个体之间在社交媒体平台上构成一张图，网络中保留了每个人特有的痕迹，包括用户发布的内容、点赞、评论、关注关系等。这些数据可以用于推荐系统推送，也可在刑事侦查方面，追踪嫌疑人的活动轨迹、人际关系等，辅助案件侦破。​
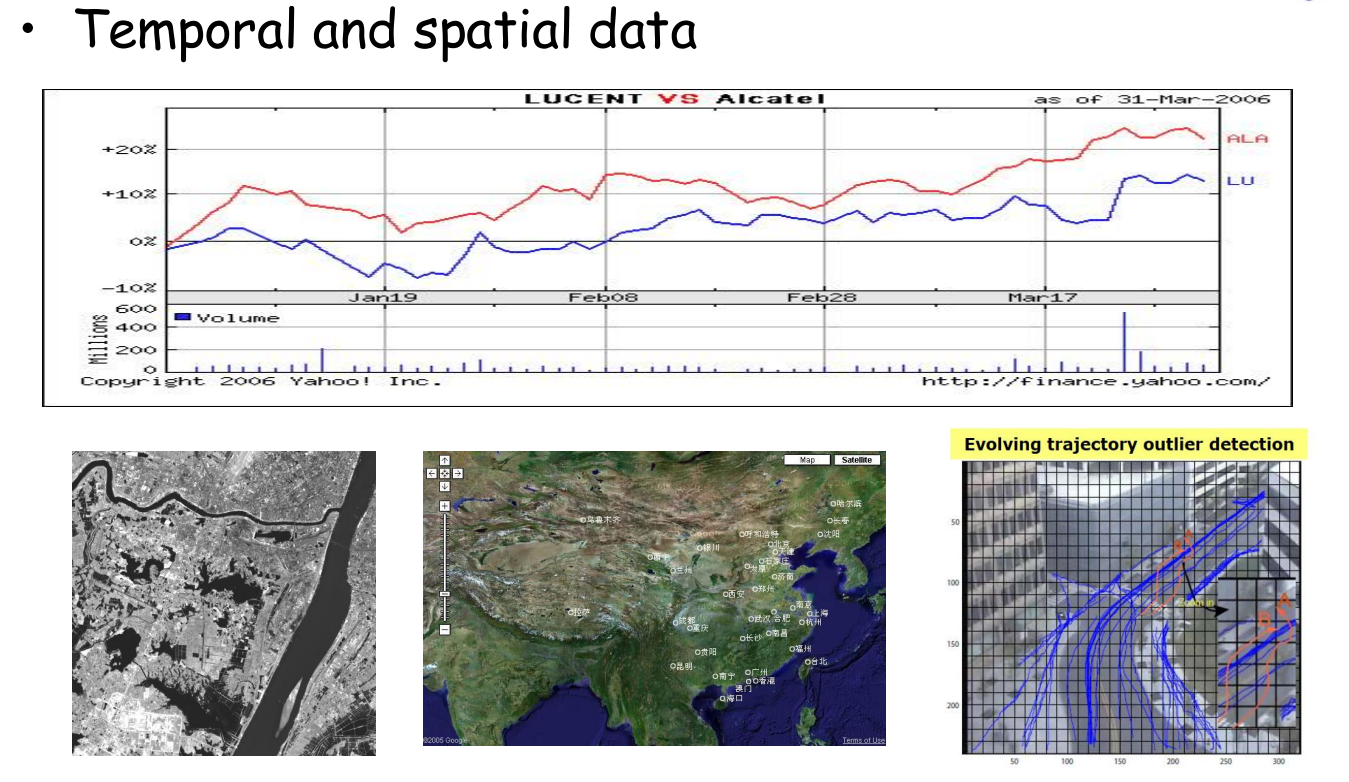
3. 时间空间数据（temporal and spatial data）：这类数据具有时间和空间上的特性，需要考虑数据在不同时间点和空间位置上的变化规律。
   • 天气预报，收集不同地区、不同时间的气温、气压、湿度等气象数据，预测未来的天气变化。
   • 交通领域，不同时间段和不同路段的变化情况。​

4. 描述性数据挖掘 + 预测性数据挖掘

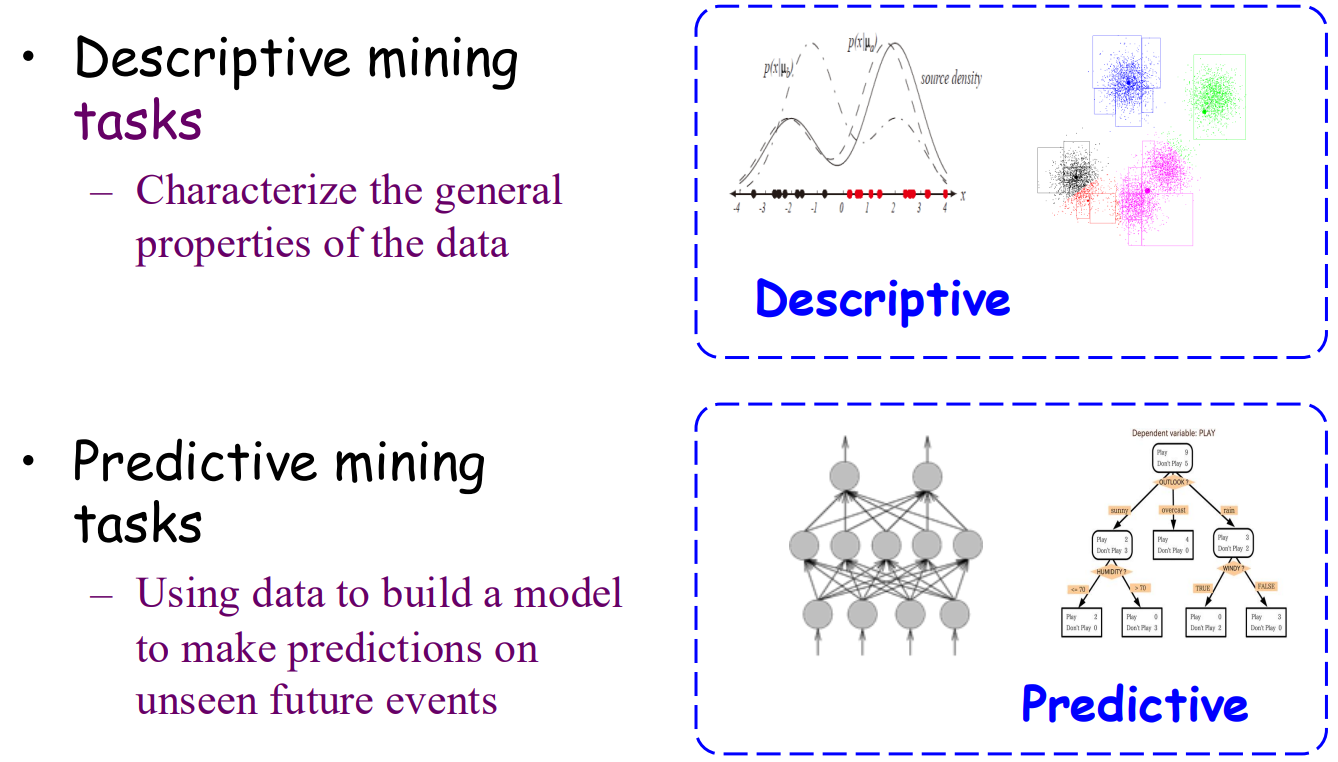
描述性数据挖掘：

• 特征总结：概括数据集中对象的一般特征，如分析学生群体的年龄、性别和成绩分布。

• 关联分析：发现数据之间的关联关系，例如商品购买中的啤酒与尿布组合。

• 聚类分析：基于相似性（如欧氏距离或余弦相似度）将数据分组，如按消费行为对客户分群以制定精准策略。

预测性数据挖掘：

• 分类：通过已有标签数据构建模型，预测新数据的类别，如邮件过滤或肿瘤诊断。

• 回归：建立变量间数学模型以预测数值结果，如房价或销售额预测。

• 异常分析：识别并分析显著偏离常规的数据点，应用于工业监控或金融反欺诈等领域。

5. Attribute types属性类型

        Nominal scale（名义尺度）编码只代表“类别”  比如 {1,2,3} 分类 也没有好坏大小之分

        Ordinal scale（顺序尺度） 值表征某个角度的好坏序列关系 （只表示 3 > 2 >1 并且3不代表比1大2）

        Numerical scale（数值尺度） 真正意义上的 可以用于大小算术计算

        Ratio scale（比率尺度）有绝对零点，乘除倍数也具有实际意义，如体重、时间、距离等。

        Interval scale（区间尺度）具有连续变化特性，但零点定义相对随意，可以作差表示差异。

        开尔文温度属于前者，摄氏度属于后者。

6. 隐私保护 -> 汇聚数据

        在数据处理过程中，防止数据泄露至关重要，隐私保护数据挖掘应运而生。其目标是在不泄露个人信息的前提下，汇聚的个人信息，将其转化为对全局有价值的信息。

        例如，在医疗数据挖掘中，可以通过对大量患者的病历数据进行分析，得出疾病的流行趋势、治疗方案的有效性等全局信息，同时又不暴露任何一位患者的个人隐私信息。​

7. 图像展示数据

一、单变量数据可视化

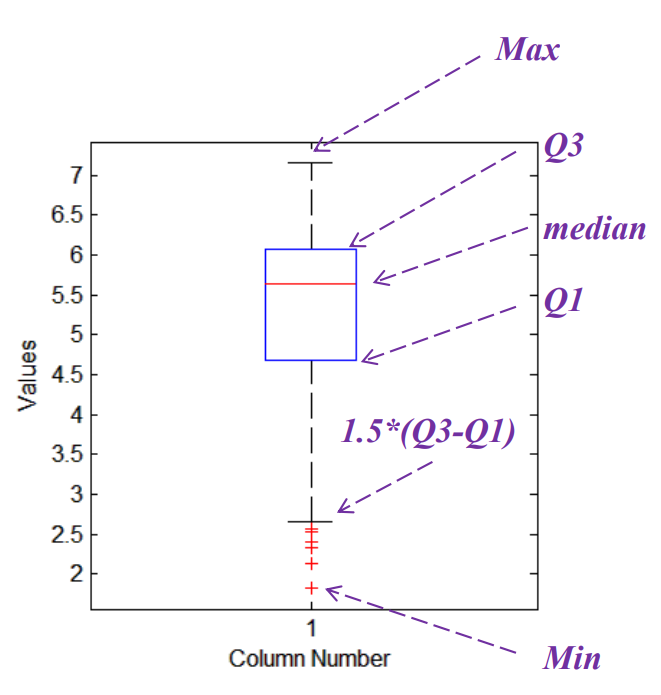
1. 箱型图 (Boxplot)

   • 作用：展示数据分散情况，识别异常值。

   • 五要素：最小值、Q1(下四分位数)、中位数、Q3(上四分位数)、最大值。

   • 异常值：小于 Q1 - 1.5IQR 或大于 Q3 + 1.5IQR（IQR = Q3 - Q1）。

   • 优点：对异常值不敏感，能稳定显示数据分布。

                        

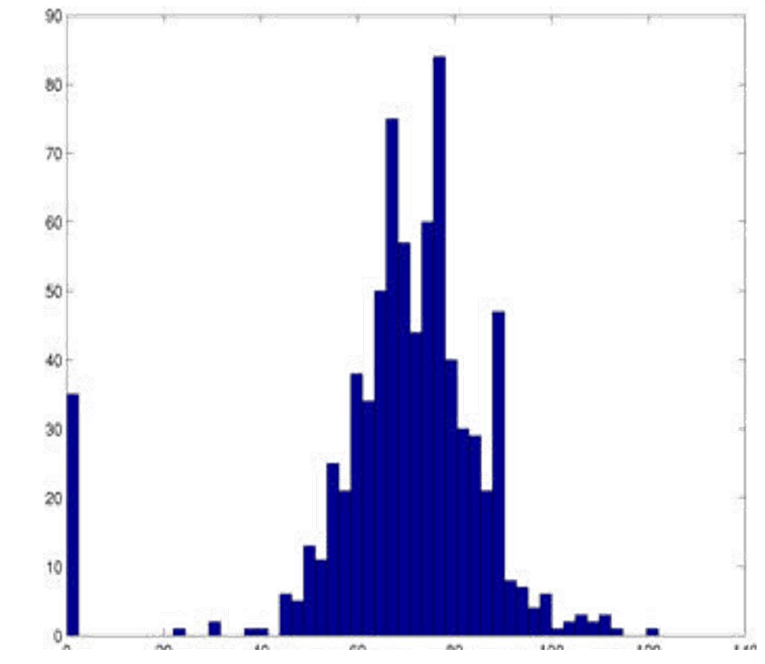
1. 直方图 (Histogram)

   • 作用：展示数据在各个区间的分布频率。

   • 关键：合理确定分组数（bin），平衡细节与整体趋势。

   • 绘制：矩形高度代表对应区间内数据点的数量。

                

二、双变量数据可视化

1. 散点图 (Scatterplot)

   • 作用：研究两个变量之间的相关关系（如线性、非线性）。

   • 绘制：将两个变量分别映射到x轴和y轴，每个数据点为一个坐标。

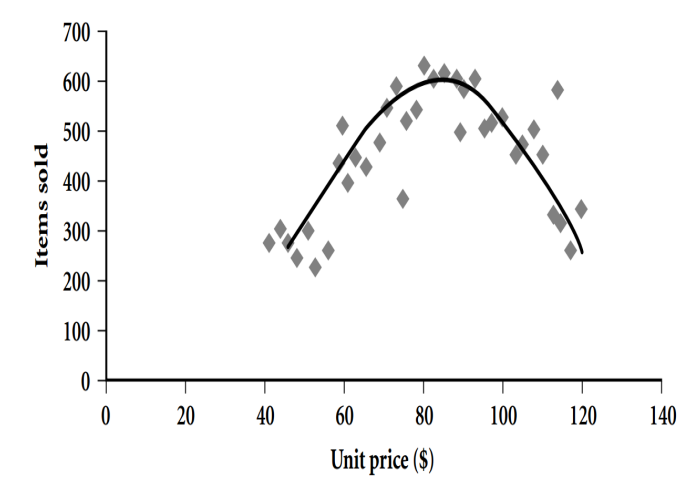
2. Loess 图 (Loess Plot)

   • 作用：在散点图基础上，通过局部加权回归拟合出一条平滑曲线，更清晰地揭示变量间的潜在趋势，尤其适用于波动较大的数据。

   • 

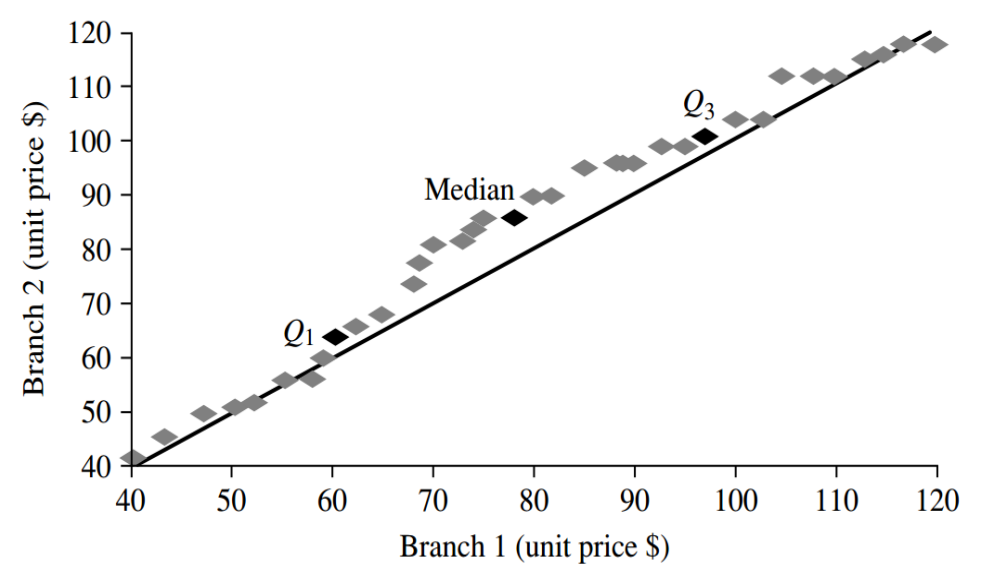
3. Q-Q 图 (Q-Q Plot)

   • 作用：检验数据是否服从某种理论分布（如正态分布）。

   • 原理：对比样本分位数与理论分位数。若点大致呈一条直线，则服从该分布。

   • 

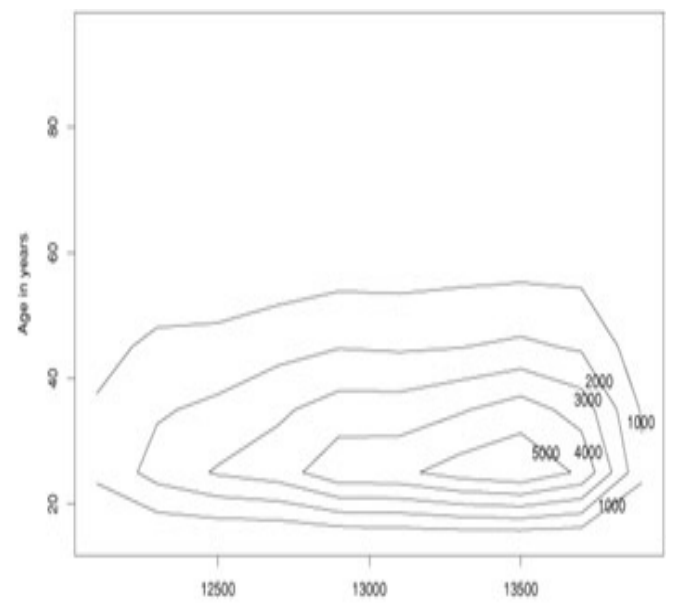
4. 等高线图 (Contour Plot)

   • 作用：展示二维散点的密度分布。

   • 原理：连接密度相同的点。线条越密集，表示该区域数据点越集中。

   • 

8. Similarity 相似性分析 - 距离度量

https://blog.csdn.net/nju_spy/article/details/149442782#t1

距离度量 metric （距离不完全等于相似度  只是某一种相似度）

距离的三个要求/性质：非负性（距离为0就是自己）；对称性；三角不等式 直递性。

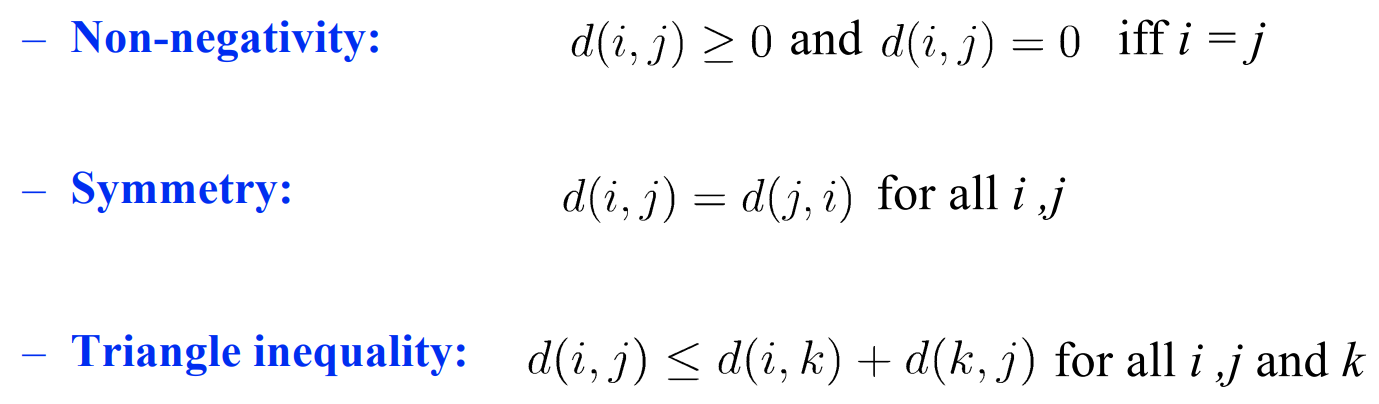
但实际任务会出现情况：人-马距离 > 人-半人马 + 马-半人马

我认为他是我好哥们，但他不一定这么觉得。 就不满足距离的特性。

闵可夫斯基距离 （Minkowski）每个维度贡献都一样；

不同的p 产生距离家族（p=1曼哈顿距离  p=2 欧式距离）。

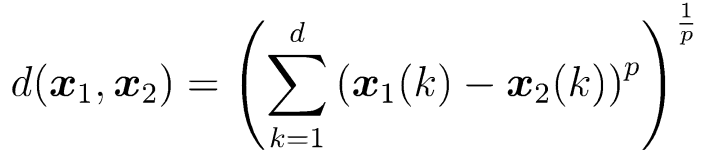
1. 归一化 (Normalization): 在计算距离前，先对每个维度进行标准化（如Min-Max, Z-Score），消除量纲影响。

2. 加权: 对求和项引入权重系数 w，以体现不同维度的重要性。

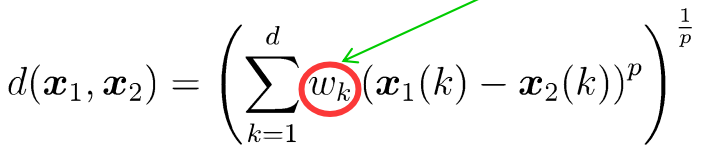
马氏距离（Mahalanobis Distance）

• 作用：通过引入协方差矩阵的逆 Σ⁻¹，马氏距离将数据投影到一个新的空间。在这个新空间里，数据的各个维度被标准化（方差变为1），并且消除了相关性（协方差变为0）。

• 效果：它相当于一个考虑了数据分布的弹性尺子。在数据点密集的方向上，距离会相对“拉长”（更敏感）；在数据点稀疏的方向上，距离会相对“缩短”（更不敏感）。最终，它测量的是点在数据分布中的标准差距离。

标称属性 (Nominal) 的距离度量 - VDM

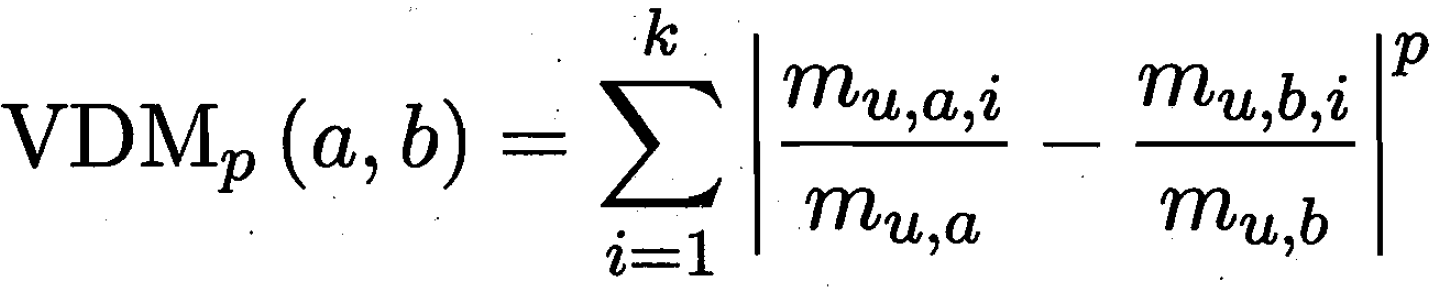
对属性u的两个种属性 a b；在k个类别群体的分布

比如 对食物属性的两种 牛奶和可乐，在k个目标人群（青年中年老年）购买的比例。

这两种购买年龄群体分布 的距离，展示了牛奶和可乐的距离。

度量学习 Metric Learning；根据data的类别 学习数据的距离关系；

距离度量学习 from 周志华《机器学习导论》第10章 降维与度量学习

• 核心思想: 让机器从数据中自动学习一个最优的距离度量函数，而不是手动选择（如欧氏距离、马氏距离）或设计（如VDM）。

• 目标: 学习一个变换，将数据投影到一个新的空间。在这个新空间中：

  • 同类样本之间的欧氏距离尽可能小。

  • 异类样本之间的欧氏距离尽可能大。

9. 高质量数据

Low Variance (低方差)  在相同条件下重复测量或收集，结果波动很小。

Low Bias (低偏差)  数据是准确且无系统误差的。   数据的平均值与真实值非常接近。

分布偏差 Polulation Drift  收集的样本要能代表总体：

例：飞机机翼 幸存者偏差

飞回来的飞机 严重受损都在机翼，机翼是最需要保护的吗？实则发动机被打坏的，都飞不回来。

这个例子收集的数据是 飞回来的样本，而不是整体的样本，出了分布偏差。

预处理三大步骤：数据清洗；数据转换（标准化）；数据约简（减少特征数）

10. Data Cleaning 数据清洗

1. 处理缺失值 (Handling Missing Data)

Ignore the tuple 删掉那一行/列；

numerical数据的话：平均值（整张表 或放在某个群体）；nominal数据的话：最多的那类；

根据其他 Attribute 相关性。

2. 平滑噪声数据 (Smoothing Noisy Data)

Noise：和正常数据差异、离群

Binning partition 划分；区间等宽 或者 每个桶元素数相同。再用平均数代替一组。

通过聚类 / 回归  找到异常点去掉

Data editing 局部有没有和邻居差的比较多的点；全局上 相对整个数据集的异常点。

3. 处理不一致性 (Handling Inconsistency)

• 来源：通常源于不同的数据源、数据录入错误或数据集成问题。

  • 例如：年龄 = “22”，出生年份 = “1990” (在2023年，这不一致)。

  • 例如：同一个人的职业在不同记录中分别为“教师”和“老师”。

数据约简 reduction 减少数据特征数，防止过拟合等问题。

可以通过 sample 采样用少数样本代替原数据：随机 / 分层

还可通过一些 降维和特征选择 算法。

周志华《机器学习导论》第10章 降维与度量学习

周志华《机器学习导论》第11章 特征选择与稀疏学习