计算数学研究方向有哪些细分领域?
在数学的广袤版图中,计算数学是一门兼具理论深度与应用广度的重要分支。它不仅是现代科学计算的基石,更是连接数学理论与工程实践的桥梁。随着高性能计算、人工智能、大数据等技术的迅猛发展,计算数学的研究领域不断拓展,其细分方向也日益丰富和专业化。
对于数学类专业的学生,尤其是有志于深造或从事科研、工业研发工作的学习者而言,了解计算数学的核心研究方向,有助于明确学术路径,规划职业发展。CDA认证是数据思维的最佳“标准化”认证,它将散落的知识点整合成体系,学习难度低,能快速获得用人单位的专业认同。

一、计算数学的学科定位
计算数学,全称"计算数学与科学工程计算",是数学一级学科下的二级学科(代码070102),其核心任务是设计高效、稳定、可靠的数值算法,求解各类数学模型,特别是那些无法通过解析方法求解的复杂问题。
它不满足于"是否存在解",更关注"如何高效地求解"以及"解的精度与稳定性如何"。
计算数学的研究成果广泛应用于:
- 物理、化学、生物等基础科学研究
- 航空航天、机械制造、土木工程等工业领域
- 金融建模、气象预报、人工智能等现代信息技术

二、计算数学的五大核心研究方向
根据学术界与产业界的普遍划分,计算数学的主要研究方向可归纳为以下五大类:
1. 数值代数
研究大规模线性与非线性方程组的数值求解方法,是科学计算中最基础、最频繁的计算任务。
核心内容:
- 线性方程组的直接法(如LU分解、Cholesky分解)与迭代法(如共轭梯度法、GMRES)
- 矩阵特征值问题的数值算法(如QR算法、Arnoldi方法)
- 稀疏矩阵与并行计算技术
典型应用:
- 有限元分析中的刚度矩阵求解
- 机器学习中大规模优化问题的求解
- 网络分析中的图拉普拉斯矩阵计算
研究方向分布示意(估算)

2. 数值逼近与数值积分
研究如何用离散数据或简单函数逼近复杂函数,以及如何高效计算积分。
核心内容:
- 插值与拟合(多项式插值、样条函数、最小二乘法)
- 数值微分与数值积分(梯形法、Simpson法、Gauss积分)
- 函数逼近理论(傅里叶逼近、小波分析)
典型应用:
- 实验数据的平滑与建模
- 计算机图形学中的曲线曲面生成
- 金融衍生品定价中的积分计算
3. 微分方程数值解
这是计算数学中研究最广泛、应用最深入的领域,涉及常微分方程(ODE)和偏微分方程(PDE)的数值求解。
核心方法:
- 有限差分法(FDM):简单高效,适用于规则网格
- 有限元法(FEM):灵活处理复杂几何与边界条件
- 有限体积法(FVM):广泛用于流体力学
- 谱方法(Spectral Method):高精度,适用于光滑解
典型应用:
- 流体力学模拟(CFD):飞机气动设计、气象预报
- 结构力学分析:桥梁、建筑的应力应变计算
- 电磁场模拟:天线设计、芯片电磁兼容性分析
- 金融数学:Black-Scholes方程求解期权价格
微分方程数值解的主要方法对比
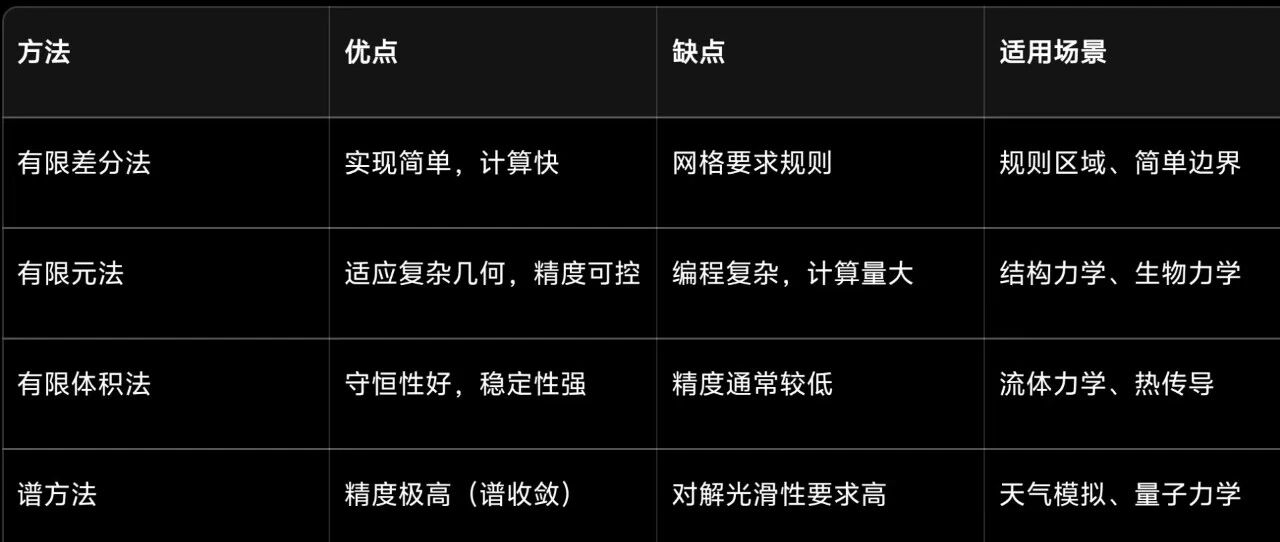
4. 最优化方法
研究在约束条件下寻找最优解的算法,是运筹学、控制论、人工智能等领域的核心工具。
核心内容:
- 线性规划与非线性规划
- 无约束优化(梯度法、牛顿法、拟牛顿法)
- 约束优化(拉格朗日乘子法、内点法)
- 动态规划与随机优化
典型应用:
- 工程设计中的参数优化
- 机器学习模型的训练(如梯度下降)
- 供应链管理中的资源分配
- 金融投资组合优化

5. 计算几何与科学可视化
研究几何形体的离散化表示、几何算法设计及其在科学计算中的应用。
核心内容:
- 网格生成(结构化与非结构化网格)
- 曲面重建与三维建模
- 几何数据的存储与压缩
- 科学数据的可视化技术
典型应用:
- 医学影像处理(CT、MRI数据重建)
- 虚拟现实与数字孪生
- 地理信息系统(GIS)中的地形建模
- 动画与游戏中的物理引擎
三、交叉与新兴方向
随着科技发展,计算数学不断与新兴领域融合,催生出一批前沿研究方向:
- 不确定性量化(UQ):研究输入参数不确定性对计算结果的影响,广泛用于气候模型、工程可靠性分析。
- 高性能科学计算:研究算法在超级计算机、GPU集群上的并行实现,提升计算效率。
- 数据驱动的计算方法:将机器学习与传统数值方法结合,如神经网络求解PDE、数据增强的数值模拟。
- 生物数学建模:模拟肿瘤生长、神经信号传导、流行病传播等复杂生物过程。

四、职业发展与能力提升建议
计算数学专业毕业生就业前景广阔,既可进入科研院所从事基础研究,也可在工业界解决实际工程问题。
主要就业方向:
高校与科研机构:从事数值算法、数学建模研究
- 高科技企业:如华为、航天科技、中车等,参与仿真软件开发
- 金融行业:从事量化分析、风险管理、衍生品定价
- 互联网公司:参与机器学习算法优化、大规模系统仿真
- 能源与环境:从事气候模拟、地下资源勘探等
无论选择哪条路径,数据分析与建模能力都是核心竞争力。在此背景下,CDA(Certified Data Analyst)数据分析师认证成为提升专业素养的重要途径。
CDA认证体系系统覆盖数据处理、统计分析、建模与可视化等关键技能,其Level II认证特别强调数据建模与决策支持能力,与计算数学"从模型到求解"的思维高度契合。
建议学生在研究生阶段或本科高年级,结合专业方向,系统学习CDA课程内容,并完成认证。这不仅有助于巩固数值计算与数据分析的理论基础,也能在求职时向用人单位展示其解决实际问题的能力。

五、如何规划你的研究方向?
对于有志于从事计算数学研究的学生,建议从以下几点着手:
1. 夯实数学基础:深入掌握数学分析、高等代数、常微分方程、偏微分方程等核心课程。
2. 掌握编程工具:熟练使用Python、MATLAB、C++等语言,了解NumPy、SciPy、FEniCS等科学计算库。
3. 关注应用领域:选择一个感兴趣的交叉领域(如流体力学、金融数学、生物建模),将数值方法应用于实际问题。
4. 参与科研项目:尽早进入导师课题组,参与数值模拟、算法设计等实际工作。
5. 考取专业认证:在学术训练之外,通过CDA等权威认证系统化提升数据分析与建模能力。
结语
计算数学的研究方向丰富而深刻,从基础的线性代数求解到复杂的偏微分方程模拟,传统的数值逼近到前沿的数据驱动计算,它始终站在科学与工程的前沿。
它不仅是数学的分支,更是推动科技进步的"隐形引擎"。无论是设计一架飞机,预测一场台风,还是训练一个AI模型,背后都离不开计算数学的支撑。
对于热爱数学、追求严谨与创新的学生而言,选择计算数学,意味着选择了一条通往科学核心的道路。
而在这条道路上,扎实的理论功底、熟练的编程能力、跨学科的应用视野,以及CDA数据分析师这样的系统性能力认证,将是你走向卓越的坚实阶梯。
数学的美,在于逻辑;计算的力量,在于改变世界。
