小明打砖块-算法

题目

最近做了小米2024年的笔试题-小明打砖块，类似于开心消消乐，对于相邻的相同砖块可选择一消，二消，三消。一消得分a，二消得分b,三消得分c，求所有砖块的最高得分。

题目链接：小明打砖块_牛客题霸_牛客网

解法

对于n个砖块，假设最高得分为maxScore(n)，那么n+1个砖块时，对于最后一个砖块而言有三种选择方案：

① 单消

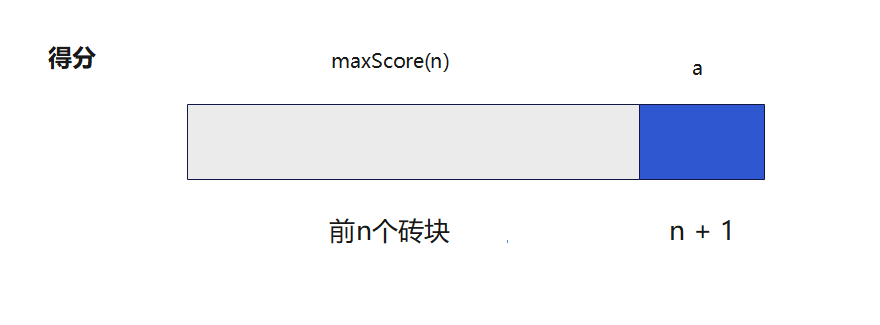
这种情况 score(n + 1) =  maxScore(n) + a

② 双消

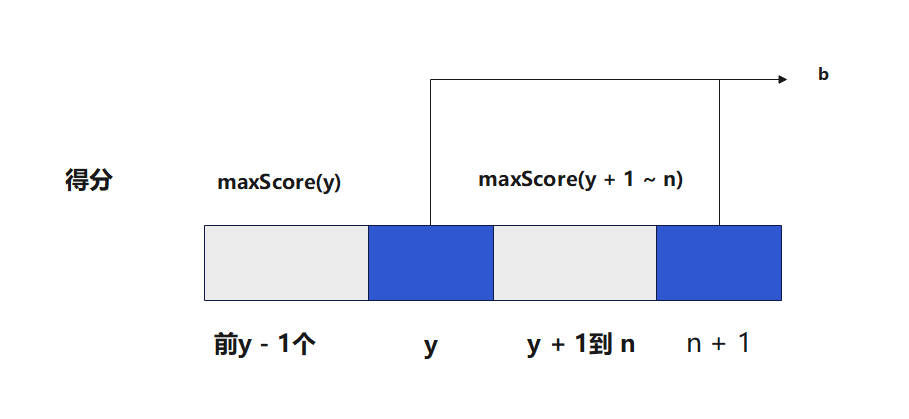
此时 score(n + 1) = maxScore(y) + maxScore(y + 1 ~ n) + b

③ 三消

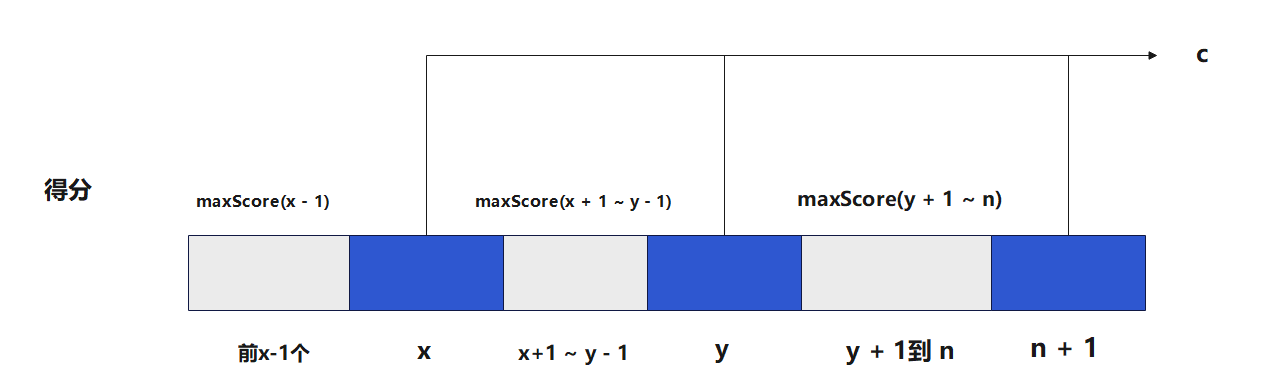
此时 score(n + 1) = maxScore(x - 1) + maxScore(x + 1 ~ y - 1) + maxScore(y + 1 ~ n) + c

因此只需要对这三种情况求出最大值就是maxScore(n + 1)

采用区间dp的思想，用dp[ i ][ j ]代表砖块下标[ i ,  j ]范围内能够获得的最高得分，求出dp后只需返回dp[0][n - 1]就是最终结果

代码实现 

import java.util.*;public class Main {public static void main(String[] args) {Scanner in = new Scanner(System.in);while(in.hasNext()) {//  砖块数量int brickSize = in.nextInt();//  消消乐得分int fade1 = in.nextInt(), fade2 = in.nextInt(), fade3 = in.nextInt();int[] bricks = new int[brickSize];for(int i = 0; i < brickSize; i++) {bricks[i] = in.nextInt();}//  动态规划//  dp[i][j]代表下标[i, j]范围内砖块的最优解int[][] dp = new int[brickSize][brickSize];for(int j = 0; j < brickSize; j++) {for(int i = 0; i <= j; i++) {//  一消dp[i][j] = fade1 + (j - 1 >= 0 ? dp[i][j - 1]: 0);//  二消if(j - i >= 1) {//  找到前一个与bricks[i]相同的元素int preIdx = j - 1;while (preIdx >= i){while(preIdx >= i && bricks[preIdx] != bricks[j]) {preIdx--;}if(preIdx >= i) {int sec1 = preIdx - 1 >= 0 ? dp[i][preIdx - 1] : 0;int sec2 = preIdx + 1 < j ? dp[preIdx + 1][j - 1] : 0;int fade2Ans = sec1 + sec2 + fade2;dp[i][j] = Math.max(dp[i][j], fade2Ans);preIdx--;}}}//  三消if(j - i >= 2) {//  找到前一个与bricks[i]相同的元素int preIdx = j - 1;while (preIdx >= i) {while(preIdx >= i && bricks[preIdx] != bricks[j]) {preIdx--;}if(preIdx >= i) {int prePreIdx = preIdx - 1;while (prePreIdx >= i) {while(prePreIdx >= i && bricks[prePreIdx] != bricks[j]) {prePreIdx--;}if(prePreIdx >= i) {int sec1 = prePreIdx - 1 >=0 ? dp[i][prePreIdx - 1] : 0;int sec2 = prePreIdx + 1 < preIdx ? dp[prePreIdx + 1][preIdx - 1]: 0;int sec3 = preIdx + 1 < j ? dp[preIdx + 1][j - 1] : 0;int fade3Ans = sec1 + sec2 + sec3 + fade3;dp[i][j] = Math.max(dp[i][j], fade3Ans);prePreIdx--;}}preIdx--;}}}}}System.out.println(dp[0][brickSize - 1]);}}
}