当前位置：首页 > news >正文

从根到叶的二进制数之和（霍纳法则）

news 2025/9/21 6:29:22

给出一棵二叉树，其上每个结点的值都是 0 或 1 。每一条从根到叶的路径都代表一个从最高有效位开始的二进制数。

例如，如果路径为 0 -> 1 -> 1 -> 0 -> 1，那么它表示二进制数 01101，也就是 13 。

对树上的每一片叶子，我们都要找出从根到该叶子的路径所表示的数字。

返回这些数字之和。题目数据保证答案是一个 32 位 整数。

示例 1：

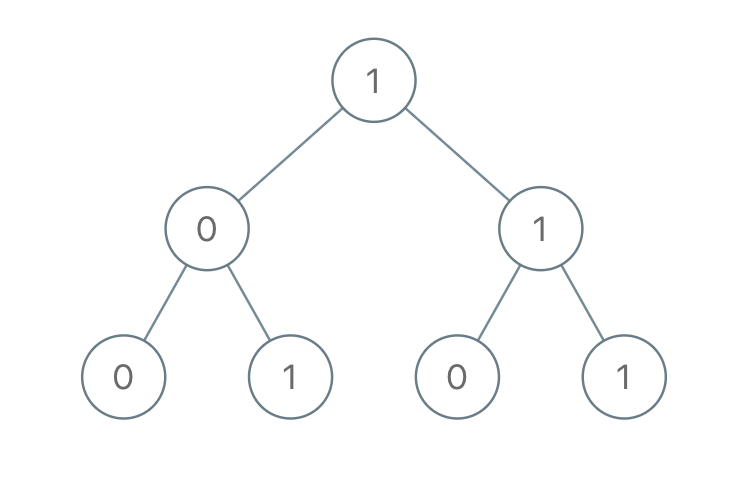
输入：root = [1,0,1,0,1,0,1]
输出：22
解释：(100) + (101) + (110) + (111) = 4 + 5 + 6 + 7 = 22

示例 2：

输入：root = [0]
输出：0

提示：

树中的节点数在 [1, 1000] 范围内
Node.val 仅为 0 或 1

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {int sum=0;void sumRoot(TreeNode* root,int pre){if(!root->left&&!root->right){//如果是叶子节点sum+=pre*2+root->val;//向左进一位再添加当前值return;}if(root->left){//如果left非空继续往下计算sumRoot(root->left,pre*2+root->val);}if(root->right){sumRoot(root->right,pre*2+root->val);}          }
public:int sumRootToLeaf(TreeNode* root) {sum=0;sumRoot(root,0);return sum;}
};

我们都知道二进制转十进制的计算为 $\sum_{i=0}^{n}a_{n}2^{n}$