01数据结构-串和KMP算法

1.串的定义

串是由0个或多个字符组成的有序序列。串中字符的个数称为串的长度，含有0个元素的串叫空串。在C语言中，可以用如下语句定义一个名为str的串。

C语言定义了’\0’作为字符串的技术标志，但在描述串的长度时，需要通过扫描整个串才获得，时间复杂度为O(N)，不如额外定义一个变量专门来存储串的长度，这样求串的长度的时间复杂度为O©的操作了。

不同的编程语言，是否用’\0’作为串的结束标语，是没有定论的，可以通过length来约束空间的长度也会更通用。例如C语言定义了一个“123”，它会认为’1’ ‘2’ ‘3’ ‘\0’，C++中的string如下图，用一个指针指向一片连续的空间，用长度来约束访问，长度为多长就代表我们的字符个数有多少个，且大部分情况我们不是从第0号开始存放，而是从1号开始存，0号可以存放一个标志位。

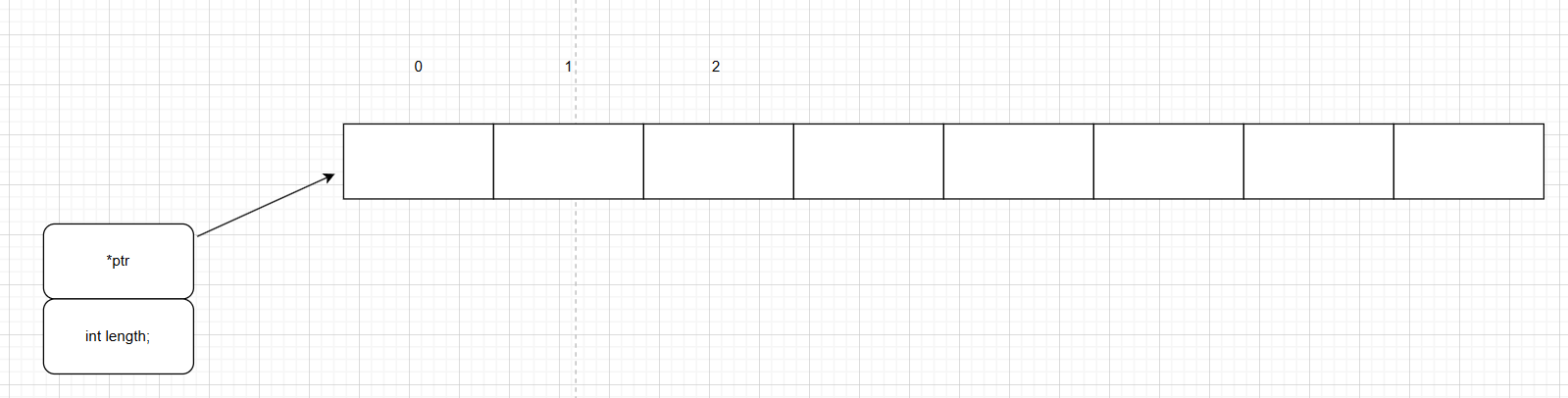
1.1定长顺序存储和变长分配存储

typedef struct{char str[maxsize+1];	// 从0号索引存数据，+1是为了存储\0int length;
}typedef struct{char *str;	// 动态分配内存;int length;
}

1.2串的初始化

与普通变量赋值操作不同，串的赋值操作不能直接用=来实现，通过定义初始化函数来实现空间拷贝。

初始化：int strAssign(StrType *str, const char *ch);

typedef struct {char *str;int length;
} StrType;
int strAssign(StrType *str,const char *ch);int strAssign(StrType *str, const char *ch) {if (str->str) {// str已经指向了数据，释放后重新再通过ch来赋值free(str->str);}// 求ch的长度int len=0;while (ch[len]) {++len;}if (len==0) {str->str=NULL;str->length=0;}else {str->str=malloc(sizeof(char)*(len+2));  // 把0号位置空出来，把\0也放入空间for (int i = 0; i <= len; ++i) {    // 包含了ch指向空间的\0位置str->str[i+1]=ch[i];}str->length=len;}return 1;
}

✅ (a) 避免空指针解引用（历史安全原因）
在C语言中，空指针NULL的地址是0。

如果字符串从索引0开始存储，那么str->str[0]可能访问地址0（空指针），在某些系统会触发错误。

从索引1开始：str->str永远不为NULL（即使字符串为空，也可能指向最小分配），str->str[0]可安全用作标志位，而str->str[1]是首字符。

✅ (b) 标志位存储元数据
索引0（str->str[0]）可存放：

长度信息（尤其短字符串时，节省存储）

引用计数（写时复制COW，但现代少用）

分配类型标志（如区分堆分配/栈内分配）

2.串的匹配

字符串模式匹配：在主串中找到与模式串相同的子串，并返回其所在位置。

例如下面长的s串我们称作为主串，下面的p串我们称为模式串。我们在s串中找p串的位置。

2.1暴力匹配

我们把s串中的每一个点都假设为我们p串中的起始点（蓝色箭头），两者同时往后遍历（红色箭头和橙色箭头），当遇到s[i]!=p[j]时s串中的起始点往后移动一位，例如：假设s中从1开始匹配，当箭头指向4即D的时候，p中的4是A，说明p串在s中的起始点不是1，因此从s再从2开始依次匹配（蓝色箭头往后移动一位），直到s中某一个点往后遍历7个位置相应的点和对应的p串中相应的点都相同我们认为找到了。

我们也可以不要蓝色的指针，当发现不匹配时，红色指针直接指向s串从遍历的起始位置的下一个索引。

暴力匹配法的核心思想是：逐个比较主串和模式串的每个字符，如果不匹配就回溯，直到找到匹配或遍历完整个主串。我们设p串中的字符个数是m个，s串中的字符个数是n个，显然采取这种方法的时间复杂度是O(mn)。

暴力匹配代码实现：

int index_simple(const StrType *str, const StrType *subStr) {int i = 1;int j = 1;int k = 1;  //记录假设值while (i<=str->length&&j<=subStr->length) {if (str->str[i]==subStr->str[j]) {++i;++j;}else {++k;j = 1;i = k;}}// 因为是从1开始存储的数据，最后若找到j会比subStr->length大1if (j>=subStr->length) {return k;}else {return 0;}
}void test01(const StrType *str,const StrType *subStr) {int res=index_simple(str,subStr);printf("simple find index:%d\n",res);
}int main() {StrType str;StrType subStr;str.str=NULL;subStr.str=NULL;strAssign(&str,"ABCDABCABCABABCABCDA");strAssign(&subStr,"ABCABCD");test01(&str,&subStr);return 0;
}

最后循环结束的时候如果j大于了subStr->length说明已找到，否则说明找不到，我们返回0。

结果：

D:\work\DataStruct\cmake-build-debug\08_KMP\kmp.exe
simple find index:13进程已结束，退出代码为 0

3.KMP

当子串和模式串不匹配时，主串指针不回溯，通过改变模式串指针的值，来确定子串从失配处和模式串的哪个位置进行比较，因为模式串前面的信息在前面比较时已经是已知信息了。

若能够存储子串失配后从模式串的哪个位置上进行比较，就可以实现KMP算法，故引入next数组，专门存放这个值。

显然，next数组里的值，只跟模式串有关，因为模式串前面已经成功匹配的字符，就表示子串中已经包含了这些字符。

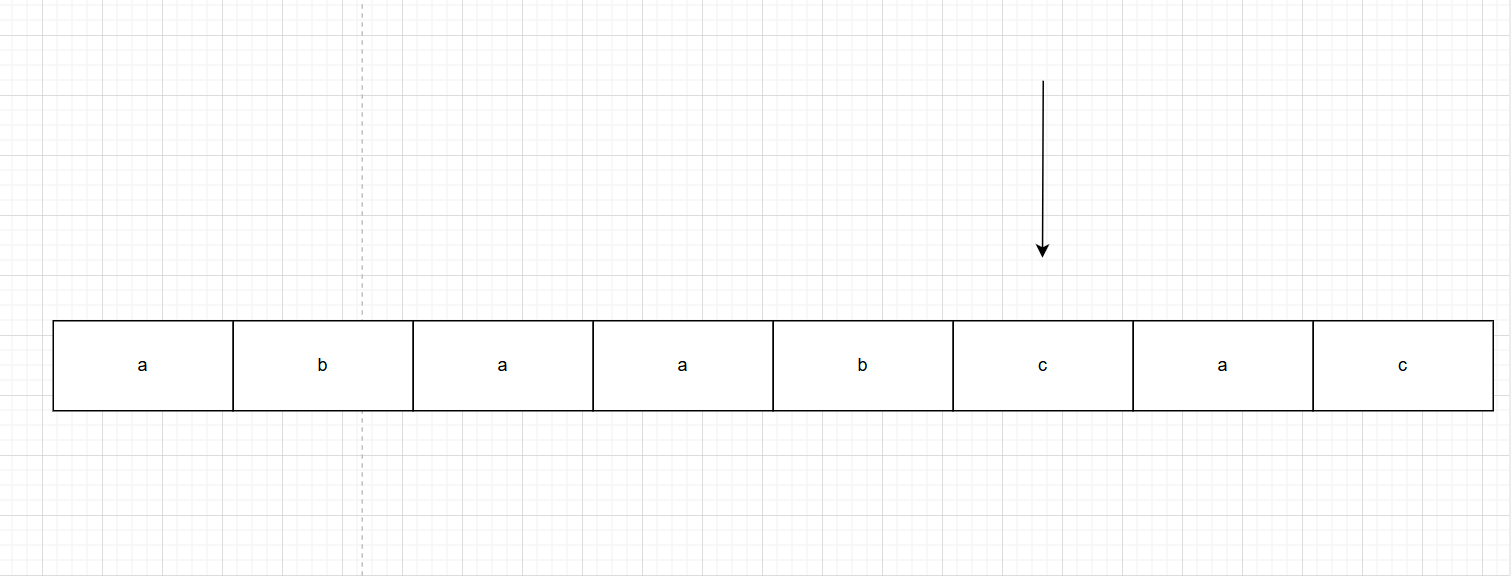
如图当我们主串匹配到6时，认为6号索引中可以存除了d的任何值，此时可以发现1-5个元素和子串中1-5号元素是匹配的，又发现由于1-2号是a和b,4-5号也是a和b，由于KMP算法是中的主串的移动指针i是不会往回走的，我们可以认为4-5号就是子串中的1-2号，子串中的移动指针从3号开始匹配，如图所示：

引入两个概念，前缀和后缀。
如图假设不匹配的点在图中的c

前缀有：a ab aba abaa abaab
后缀有：c ac abc aabc baabc

next数组就是前缀和后缀最大的公共子序列的长度。

3.1next数组的计算

next数组定义：当主串与模式串的某一个字符不匹配时，模式串要回退的位置。

next[j]：第j位字符前面j-1位字符组成的子串的前后缀重合字符数+1（+1的原因是从失效点开始重新匹配，若不加1则是失效点的前一位）。

当j=1时，规定next[1]=0;（第一个字符都不匹配）
当j=2时，j前面的子串a，next[2]=1;

如图前两个我们认为是固定的，当失效点在3的时候，前缀和后缀没有公共子序列，所以模式串要回退到从1开始，next数组填1。

失效点在4的时候，前缀和后缀有一个公共子序列，所以模式串要回退到从2开始，next数组填2。

失效点在6的时候，前缀和后缀有两个公共子序列，所以模式串要回退到从3开始，next数组填3。

最终next数组如上图。

如果我们要在代码方面实现next数组，比如下图我们要求17号索引的值，假设16号索引next数组中的值是8，那么证明1-7号索引代表的字符和9-15号索引代表的字符是工共子序列，此时若16号索引代表的字符与8号索引代表的字符相同，那么说明索引为17的next数组中的值应填17。

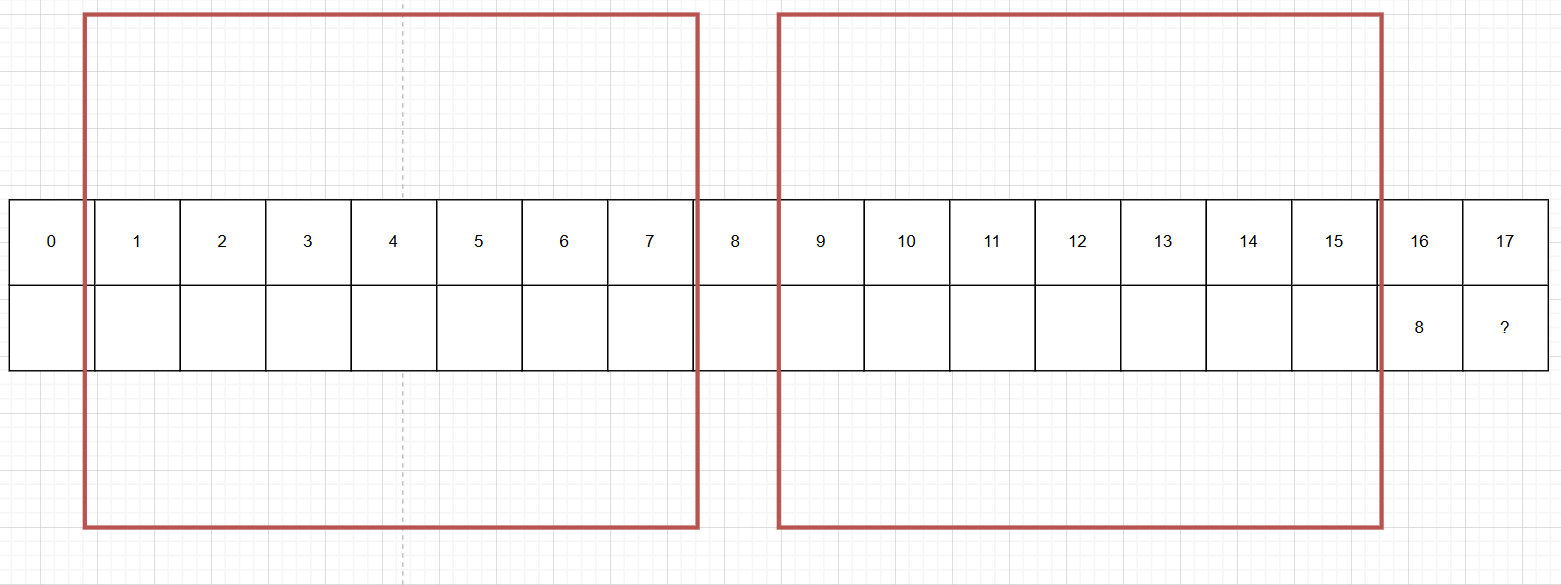
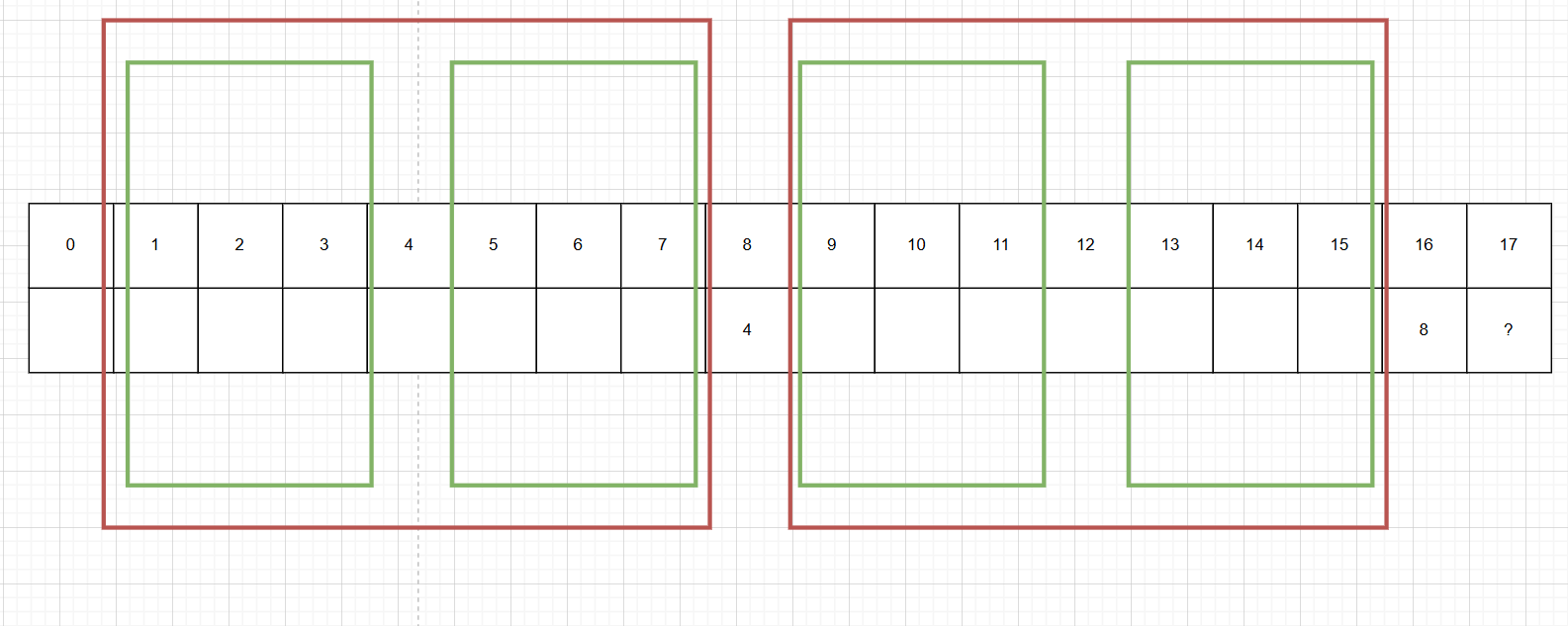
若16号索引代表的字符与8号索引代表的字符不相同，我们看8号索引对应的值，假设为4，说明1-3号索引代表的字符和5-7号索引代表的字符是相同的，又由于之前1-7号索引代表的字符和9-15号代表的字符是相同的，说明9-11号代表的字符和13-15号代表的字符也是相同的，如果16号索引代表的字符与4号索引代表的字符相同，那么说明索引为17的next数组中的值应填5。（若不等就往前面推）

3.2KMP算法代码实现

KMP算法：int index_KMP(const StrType *str, const StrType *subStr, const int *next);

int index_KMP(const StrType *str, const StrType *subStr, const int *next) {int i=1;int j=1;while (i<=str->length&&j<=subStr->length) {if (j==0||str->str[i]==subStr->str[j]) {++i;++j;}else {j=next[j];}}if (j>=subStr->length) {return i-subStr->length;}else {return 0;}
}

由于i是不会往回退的，所以最终返回的是i-subStr->length

如果没有 j==0 这个条件，算法在某些情况下可能会卡住。具体来说，当 j 被 next[j] 重置为 0 时，如果没有 j==0 这个条件，那么在下一次循环中，j 仍然是 0，而 str->str[i] 和 subStr->str[j] 的比较就会变成 str->str[i] 和 subStr->str[0] 的比较。

如果 str->str[i] 不等于 subStr->str[0]，那么 j 会一直保持为 0，导致算法无法继续前进，从而进入无限循环。

因此，j==0 这个条件的作用是确保在 j 被重置为 0 时，能够正确地将 i 和 j 都向前推进一位，继续进行比较。这样可以避免算法卡在 j=0 的情况。

next数组的计算：void getNext(const StrType *subStr,int next[]);

void getNext(const StrType *subStr,int next[]) {int i=1,j=0;        // i: 主指针, j: 前缀指针next[1]=0;while (i<subStr->length) {if (j==0||subStr->str[i]==subStr->str[j]) {++i;++j;next[i]=j;   // 这里记录的是前缀和后缀相等的长度}else {j=next[j];}}
}

🔍 i 的角色：后缀末尾指针
职责：指向当前正在考察的后缀的最后一个字符

移动规律：每次循环至少向前移动一位

最终目标：遍历模式串的每个位置，计算对应的next值

物理意义：i 指向的是我们要计算 next[i] 的位置

🔍 j 的角色：前缀匹配指针
职责：指向当前匹配的前缀的最后一个字符

移动规律：可能前进也可能回溯

核心功能：记录当前已匹配的前缀长度

物理意义：j 的值就是当前的最长相等前后缀长度

回溯 j = next[j]：当匹配失败时，找到更短的相同前后缀继续尝试

最后来测一下：

#include"findStr.h"
#include<stdio.h>
#include<stdlib.h>void test02(const StrType *str,const StrType *pattern) {int *next=malloc(sizeof(int)*(pattern->length+1));getNext(pattern,next);printf("%d\n",index_KMP(str,pattern,next));free(next);
}int main() {StrType str;StrType subStr;str.str=NULL;subStr.str=NULL;strAssign(&str,"ABCDABCABCABABCABCDA");strAssign(&subStr,"ABCABCD");test02(&str,&subStr);return 0;
}

结果：

D:\work\DataStruct\cmake-build-debug\08_KMP\kmp.exe
13进程已结束，退出代码为 0

这是数据结构的最后一篇博客，后续还会更新计算机组成原理，计算机网络，操作系统等的课程。感谢大家观看。