【Leetcode hot 100】437.路径总和 Ⅲ
问题链接
437.路径总和 Ⅲ
问题描述
给定一个二叉树的根节点 root ,和一个整数 targetSum ,求该二叉树里节点值之和等于 targetSum 的 路径 的数目。
路径 不需要从根节点开始,也不需要在叶子节点结束,但是路径方向必须是向下的(只能从父节点到子节点)。
示例 1:
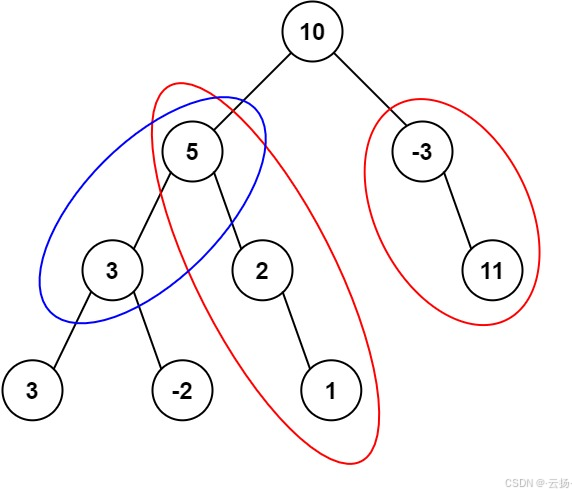
输入:root = [10,5,-3,3,2,null,11,3,-2,null,1], targetSum = 8
输出:3
解释:和等于 8 的路径有 3 条,如图所示。
示例 2:
输入:root = [5,4,8,11,null,13,4,7,2,null,null,5,1], targetSum = 22
输出:3
提示:
- 二叉树的节点个数的范围是
[0,1000] -10^9 <= Node.val <= 10^9-1000 <= targetSum <= 1000
问题解答
解法一:暴力递归(基础思路)
思路
以每个节点为起点,向下遍历所有可能的路径,计算路径和并统计符合条件的数量:
- 主函数:遍历二叉树的每个节点,对每个节点调用「路径统计辅助函数」;
- 辅助函数:从当前节点出发,递归遍历左/右子树,累加路径和,若等于
targetSum则计数+1。
代码实现
/*** Definition for a binary tree node.* public class TreeNode {* int val;* TreeNode left;* TreeNode right;* TreeNode() {}* TreeNode(int val) { this.val = val; }* TreeNode(int val, TreeNode left, TreeNode right) {* this.val = val;* this.left = left;* this.right = right;* }* }*/
class Solution {public int pathSum(TreeNode root, int targetSum) {if (root == null) {return 0;}// 1. 以当前节点为起点的路径数int currentCount = countPathFromNode(root, targetSum);// 2. 递归处理左子树(以左子树节点为起点)int leftCount = pathSum(root.left, targetSum);// 3. 递归处理右子树(以右子树节点为起点)int rightCount = pathSum(root.right, targetSum);// 总路径数 = 当前节点起点数 + 左子树起点数 + 右子树起点数return currentCount + leftCount + rightCount;}/*** 辅助函数:从当前节点出发,统计路径和等于 target 的数量* @param node 当前起点节点* @param target 剩余需要满足的路径和(每次累加节点值后递减)* @return 符合条件的路径数*/private int countPathFromNode(TreeNode node, long target) {if (node == null) {return 0;}// 记录当前节点是否满足路径和(若满足则+1)int count = 0;if (node.val == target) {count = 1;}// 递归遍历左子树:剩余目标和 = 原目标 - 当前节点值int left = countPathFromNode(node.left, target - node.val);// 递归遍历右子树int right = countPathFromNode(node.right, target - node.val);// 总路径数 = 当前节点满足数 + 左子树满足数 + 右子树满足数return count + left + right;}
}
复杂度分析
- 时间复杂度:O(n²),n 为二叉树节点数。每个节点作为起点需遍历其下方所有节点,最坏情况(链状树)下总操作数为
n + (n-1) + ... + 1 = O(n²)。 - 空间复杂度:O(n),递归栈深度取决于树的高度,最坏情况(链状树)为 O(n)。
解法二:前缀和 + 哈希表(优化思路)
思路
利用「前缀和」优化时间复杂度,核心原理:
- 前缀和定义:从根节点到当前节点的路径上所有节点值的总和,记为
currSum; - 路径和推导:若存在某一前驱节点的前缀和
prevSum,使得currSum - prevSum = targetSum,则从「前驱节点的下一个节点」到「当前节点」的路径和等于targetSum; - 哈希表作用:存储「前缀和 → 出现次数」,快速查询
prevSum = currSum - targetSum的出现次数,避免重复遍历。
关键细节
- 初始状态:哈希表需先放入
(0, 1),表示「前缀和为 0 的路径出现 1 次」(对应从根节点开始的路径,如currSum = targetSum时,prevSum = 0需计数); - 回溯操作:深度优先遍历(DFS)后需「撤销」当前前缀和的计数(次数-1,若次数为 0 则移除),避免影响其他路径的计算;
- 溢出处理:用
long存储前缀和,避免节点值累加时超出int范围。
代码实现
import java.util.HashMap;
import java.util.Map;class Solution {public int pathSum(TreeNode root, int targetSum) {// 哈希表:key=前缀和,value=该前缀和出现的次数Map<Long, Integer> prefixSumMap = new HashMap<>();// 初始状态:前缀和为 0 的路径出现 1 次prefixSumMap.put(0L, 1);// 调用 DFS 递归统计路径数return dfs(root, 0L, targetSum, prefixSumMap);}/*** DFS 递归函数:统计以当前节点为终点的符合条件的路径数* @param node 当前遍历节点* @param currSum 从根节点到当前节点的前缀和* @param targetSum 目标路径和* @param prefixSumMap 前缀和哈希表* @return 符合条件的路径数*/private int dfs(TreeNode node, long currSum, int targetSum, Map<Long, Integer> prefixSumMap) {// 递归终止条件:节点为空,无路径if (node == null) {return 0;}// 1. 计算当前节点的前缀和(累加当前节点值)currSum += node.val;// 2. 统计符合条件的路径数:查询 prevSum = currSum - targetSum 的出现次数int count = prefixSumMap.getOrDefault(currSum - targetSum, 0);// 3. 将当前前缀和加入哈希表(次数+1)prefixSumMap.put(currSum, prefixSumMap.getOrDefault(currSum, 0) + 1);// 4. 递归遍历左子树和右子树,累加路径数count += dfs(node.left, currSum, targetSum, prefixSumMap);count += dfs(node.right, currSum, targetSum, prefixSumMap);// 5. 回溯:移除当前前缀和的计数(避免影响其他路径)prefixSumMap.put(currSum, prefixSumMap.get(currSum) - 1);// 若次数减为 0,可从哈希表中删除(优化空间,非必需)if (prefixSumMap.get(currSum) == 0) {prefixSumMap.remove(currSum);}// 返回当前节点及其子树的符合条件的路径数return count;}
}
复杂度分析
- 时间复杂度:O(n),n 为二叉树节点数。每个节点仅遍历一次,哈希表的
put、get操作均为 O(1)。 - 空间复杂度:O(n),哈希表存储的前缀和数量不超过节点数,递归栈深度取决于树的高度(最坏情况 O(n))。
两种解法对比
| 解法 | 时间复杂度 | 空间复杂度 | 适用场景 |
|---|---|---|---|
| 暴力递归 | O(n²) | O(n) | 树规模较小(n < 1000) |
| 前缀和+哈希表 | O(n) | O(n) | 树规模较大,追求高效解法 |
