神经网络学习笔记16——高效卷积神经网络架构汇总(SqueezeNet、MobileNet、ShuffleNet、EfficientNet、GhostNet)

系列文章目录

---

---

前言

模型的发展

从2012年发展至今，神经网络模型经历了从卷积神经网络CNN到注意力机制Transformer等范式性的演进。然而，贯穿始终的核心研究驱动力始终围绕着两个相辅相成又看似矛盾的方向：

更大更强

追求模型的​​极致能力​​和​​认知边界突破​​。
能够学习更多的信息，捕捉更细的特征，提升泛化能力，解决开放域问题等。
目的是为了能处理更复杂的任务，比如通用人工智能、自然语言理解与生成、科学计算模拟等。主要通过增大模型参数规模、增加训练数据量、构建复杂的架构以及优化训练技术来实现这一目标。

​​更小更快

​​追求模型的​​实用效率​​和​​普适部署​​。
能够为了在能维持一定精度的前提下减少参数量和运算量。
目的是满足边缘/终端设备的低功耗、实时性、低成本、隐私保护要求，降低云端推理成本、提高响应速度，主要通过设计更高效的模型架构，进行裁剪、量化、蒸馏对模型进行压缩，优化特定算子和结合AI硬件加速来实现这一目标。

高效卷积神经网络架构

模型名称

表示轻量化神经网络模型的名称，名称中包含着几个重要信息：
1、不同的架构家族 (如 squeezenet, Mobilenet, ShuffleNet, EfficientNet, GhostNet, DeiT, ConvVT)。
2、不同的版本/变体标识 (如V1, V2, V3)。
3、不同的规模/宽度乘子 (如 0.5, 0.75, 1.0, 1.5x, 2x, -Small, -Large)。
4、其他配置参数 (如 160, 224 通常指输入图像的尺寸， g=3/8 对 ShuffleNet 指分组卷积的分组数，还有像b0/b1/b2/b3、S/M/L、A1/A2/A3、lite0/lite1/lite2/lite3/lite4等模型设置，特指不同尺寸或者不同复杂度)。

参数量

​​参数量是指模型中需要学习的参数总数。
1、参数量决定模型的内存占用（如显存和内存）和数据加载和传输时间，参数需从内存频繁读取到计算单元，高参数量可能导致​​内存带宽瓶颈​​，拖慢推理速度（尤其在移动设备）。
2、参数量与模型的​​复杂度、学习能力和表达能力有紧密关系（通常参数越多，模型越复杂，理论上拟合能力越强）。
3、参数量也是衡量模型​​“轻量化”​​程度的最关键指标之一，轻量化模型的核心目标就是在保持一定性能的前提下，尽可能减少参数量。​​

乘加运算量

乘加运算量是指模型进行一次前向推理（处理一张图片）所需完成的 ​​乘法累加操作的总次数。一次乘加运算通常指 a * b + c 这样的计算。​​
1、乘加运算量是衡量模型​​计算复杂度​​和​​推断速度​​（尤其是在硬件上）的最常用指标之一，与模型的​​耗电量​​（对移动设备尤为重要）强相关。
2、乘加运算量是衡量模型​​“轻量化”​​程度的核心指标，直接决定计算时间（如GPU/CPU的浮点运算耗时），需要在满足性能要求下降低此值。
​​3、神经网络中的主要计算（如卷积、全连接层）绝大部分都是由大量的乘加操作构成的，统计乘加次数能有效反映整体的计算负担。

评价指标

ImageNet fp32 top1 accuracy评价指标是衡量不同轻量化模型分类​​准确性的核心依据。它直观地告诉我们在识别 1000 类物体时，模型猜中“第一名”的概率是多少。用户可以通过这个值直接比较不同模型在相同的权威数据集和评估标准下的表现优劣。数值越高越好。

1、fp32是模型在运行/评估时使用的​​数值精度​​，代表 ​单精度浮点数（Single-precision floating-point format）​​，是一种在计算机中表示实数的格式，使用 32 位（4 字节）存储一个数字。有些轻量化模型在部署时可能会使用更丰富的精度选择，比如fp16、int8、int4、int2以及混合精度，通过对模型量化以加速和减小模型体积，但在学术论文和基准对比中，通常报告 fp32 精度以保证公平比较。

2、​​ImageNet数据集是一个巨大的、公开的​​图像数据集​​，具体是指 ​​ILSVRC 2012​​ 数据集（ImageNet Large Scale Visual Recognition Challenge 2012）。它包含超过 ​​140万​​ 张训练图像，​​5万​​ 张验证图像，​​10万​​ 张测试图像，涵盖了 ​​1000 个不同的物体类别​​（如“猫”、“狗”、“汽车”、“杯子”等）。

3、top1 accuracy是评估图像分类任务最直接、最重要的​​性能指标​​。在推理过程中对验证/测试集中的每一张图片都会输出一个包含 1000 个类别的​​概率分布也就是置信度​。而​​top1 accuracy指的是模型预测的​​概率最高的那个类别恰好等于图片真实标签的比例​​。有时还会使用top5 accuracy​​，它指的是​​图片的真实标签出现在模型预测的前5个最高概率类别之中的比例​​。​​

高效卷积神经网络的比较

---

一、SqueezeNet

SqueezeNet论文地址

1、优化策略

1.优化一

替换卷积核：
使用 1×1卷积替代大部分 3×3卷积，1×1卷积的参数量仅为3×3卷积的1/9，且能实现跨通道交互，显著降低计算复杂度。

2.优化二

减少输入通道数：
使用 1×1卷积压缩输入通道数，比如减少至原尺寸的 1/n，降低后续计算复杂度，

3.优化三

延迟降采样：
将池化层后移至网络中后段，保留更多高分辨率特征图，提升分类精度。

2、模型结构

SqueezeNet 的其核心创新在于 ​​Fire Module​​ 的设计，由 ​​Squeeze 层​​和 ​​Expand 层​​组成。输入特征图首先通过 ​​Squeeze 层​​进行通道数的压缩，然后通过 ​​Expand 层​​进行通道数的扩张。这两个层通过参数高效的结构，在保持模型精度的同时显著减少计算量和存储需求。

1.​Squeeze 层​​

Squeeze层负责压缩输入特征图的通道数，减少后续计算量。通过 1×1 卷积实现​​通道降维​​，在网络中创造了一个瓶颈层，使网络在低维度空间学习输入数据的​​压缩表示​​，只保留最核心的信息，丢弃冗余信息。

将通道数从 C_input压缩至 C_squeeze（C_squeeze < C_input），输出特征图的尺寸由 H x W x C_input 变为 H x W x C_squeeze，注意空间尺寸 H x W 保持不变​​。

在Squeeze层后添加ReLU激活函数，引入非线性表达能力，避免信息损失。

2.​Expand 层

Expand层负责接收 Squeeze 层输出的低维特征，通过并行卷积路径​​扩展通道数并融合多尺度信息​​。在 Squeeze 层进行了强力压缩之后，需要通过增加通道数并提供不同尺寸的卷积核来保持网络的表达能力。

​​1×1 卷积路径​​：使用填充padding为0，步长​stride为1的$e_{₁}$个 1 x 1 卷积核，捕捉局部感受野的空间特征，参数量小且计算高效。
​​3×3 卷积路径​​：使用填充padding为1，步长​stride为1的$e_{₃}$个 3 x 3 卷积核，捕捉更大感受野的空间特征，增强模型对复杂模式的识别能力。

通道拼接：H x W大小的特征图经过1×1 卷积核计算得到的新特征图为H x W大小，经过3×3 卷积核计算得到的新特征图依然为H x W大小，所以两条路径输出得新特征图大小一致，可以在通道维度进行拼接，形成最终的高维特征。

Expand层中的 ​​1 x 1 和 3 x 3 卷积并联​​提供了不同大小的感受野，拼接它们的输出相当于在网络底层就融合了​​不同尺度的特征​​，有助于模型捕获更丰富的信息。

在Expand层后添加ReLU激活函数，引入非线性表达能力，避免信息损失。

3.Fire Module模块

一个完整的 Fire Module由Squeeze-Expand组成：

Squeeze层：​​
1x1 卷积 (s₁个核)。

Expand层:
并行分支 1：​​ 1 x 1 卷积 (e₁个核)。
并行分支 2：​​ 3 x 3 卷积 (e₃个核)。

**​​超参数：**​​

s₁: Squeeze 层输出的通道数 (也是 Expand 层两路分支共同的输入通道数)。
e₁: Expand 层 1 x 1 分支的输出通道数。
e₃: Expand 层 3 x 3 分支的输出通道数。

​​通常满足：​​ s₁ < (e₁ + e₃)。即先压缩通道，再扩增通道。

Fire Module模块通过​​先大幅压缩通道数建立瓶颈，再在低维空间高效地利用多尺度卷积扩展通道​​的设计，在​​显著降低参数数量和计算量​​的同时，努力​​保持网络的准确率​​。

input：224 x 224 x 3
conv1：7×7卷积，stride=2，降采样（224×224→111×111），输入特征矩阵通道扩展为96通道
maxpool1：3×3池化，进一步降采样（111×111→55×55），维持96通道
​​fire2：Squeeze-Expand结构，96通道压缩为16通道，输出128通道
​​fire3：Squeeze-Expand结构，128通道压缩为16通道，输出128通道
​​fire4：Squeeze-Expand结构，128通道压缩为32通道，输出256通道
maxpool4：3×3池化，进一步降采样（55×55→27×27），维持256通道
​​fire5：Squeeze-Expand结构，256通道压缩为32通道，输出256通道
​​fire6：Squeeze-Expand结构，256通道压缩为48通道，输出384通道
​​fire7：Squeeze-Expand结构，384通道压缩为48通道，输出384通道
​​fire8：Squeeze-Expand结构，384通道压缩为64通道，输出512通道
maxpool8：3×3池化，进一步降采样（27×27→13×13），维持512通道
​​fire9：Squeeze-Expand结构，512通道压缩为64通道，输出512通道
conv10：1×1卷积，stride=1，512通道扩展为1000通道，对应000个类别
avgpool：空间维度压缩（13×13→1×1），生成类别概率向量
softmax：输出预测结果

表中右边的量化内容与该模型结构关系不大，不在这里展开解释。

左侧模型：标准直流SqueezeNet模型
遵循经典 ​​SqueezeNet 架构​​，由输入输出层、conv、maxpool、fire模块、池化层和softmax回归构成，数据严格按顺序流动。
​​
中间模型：跳跃连接SqueezeNet模型
添加残差连接​​，解决如果模型网络过深导致的梯度消失和梯度爆炸问题，加速模型收敛，增强模型泛化能力。
将输出通道和输入通道一致的层进行残差连接：fire2-fire4，maxpool4-fire5，fire6-fire8，maxpool8-conv10。

​​右侧模型：复杂旁路SqueezeNet模型
添加conv1x1卷积旁路​​，结合残差连接确保每一层都能复用上上层的特征数据，使得低层特征信息与高层特征信息能够深度融合。
将输出通道和输入通道不一致的层进行卷积处理然后相连：maxpool2-fire3，fire3-maxpool4，fire5-fire7，fire7-maxpool8。

---

二、MobileNet

1、Mobilenet v1

Mobilenet v1论文地址

1.标准卷积Convolution

$$F_{std}=D_K\cdot D_K\cdot M\cdot N\cdot D_F\cdot D_F=D_K^2\cdot M\cdot N\cdot D_F^2$$

​​$D_K$​​: 卷积核的空间尺寸（高度/宽度）。通常表示为 K或 Kernel Size。例如，一个 3x3的卷积核，$D_K$ = 3。
​​M​​: 输入特征图的通道数（Input Channels / Depth）。
​​N​​: 输出特征图的通道数（Output Channels / Depth）。
​​$D_F$: 输出特征图的空间尺寸（高度/宽度）。通常取决于输入尺寸、卷积核大小、步长（Stride）和填充（Padding）。

为了计算输出特征图 ($D_F\cdot D_F$) 上某个位置​​的​​某一个输出通道 (N)​​ 的值，需要将卷积核 ($D_K\cdot D_K$) 在输入特征图上对应的局部区域 ($D_K\cdot D_K$) 滑动覆盖。

卷积核有M个通道（与输入通道数匹配），对于输入特征图的每一个输入通道 (M)​​，都需要用该通道对应的$D_K\cdot D_K$卷积核与输入特征图上对应位置的$D_K\cdot D_K$区域做逐元素相乘。

然后将 M个通道上所有的乘积结果相加​​，得到该输出像素上该输出通道的值。所以计算一个输出像素的一个输出通道需要$D_K\cdot D_K\cdot M$次乘法操作。

​​扩展到所有输出像素和所有输出通道：​​
输出特征图有$D_F\cdot D_F$个空间位置（像素）。
输出特征图有 N个通道。
因此，总乘法操作数$F_{std}$ = (单个像素单个通道的计算量) * (像素总数) * (输出通道数)。

2.深度可分离卷积Depthwise Separable Convolution

$$F_{dws}=D_K\cdot D_K\cdot M\cdot D_F\cdot D_F+M\cdot N\cdot D_F\cdot D_F=D_K^2\cdot M\cdot D_F^2+M\cdot N\cdot D_F^2$$

深度卷积：​​
对每个输入通道​​独立​​应用一个空间卷积。卷积核尺寸是$D_K\cdot D_K$。​​关键点在于输入通道数M也是DW输出通道数（深度卷积的输出通道数等于输入通道数）。每个输出通道只由对应的一个输入通道计算得来，通道之间没有信息混合。

计算单个输出像素的单个（唯一与之对应的）输出通道（深度卷积的输出通道数 = M），只需要$D_K\cdot D_K$次乘法（作用于单个输入通道上），输出特征图（深度卷积的输出）有$D_F\cdot D_F$个像素和M个通道。

深度卷积总乘法操作数 = (单个像素单个通道的计算量) * (像素总数) * (输出通道数)。

​​逐点卷积：​​
将深度卷积输出的 M个通道通过 1 × 1 卷积组合起来，转换成所需的 N个输出通道，实际就是一个$M_K=1$的标准卷积。

计算单个输出像素的单个输出通道需要 $1\cdot 1\cdot M$次乘法（1 × 1 卷积核作用于所有 M个输入通道上，然后相加）。输出特征图（最终输出）有$D_F\cdot D_F$个像素和 N个通道。

逐点卷积总乘法操作数 = (单个像素单个通道的计算量) * (像素总数) * (输出通道数)

​​深度可分离卷积总计算量：​​
将上述两步的计算量相加：$F_{dws}$ = (深度卷积计算量) + (逐点卷积计算量)

$$\frac{D_K\cdot D_K\cdot M\cdot D_F\cdot D_F+M\cdot N\cdot D_F\cdot D_F}{D_K\cdot D_K\cdot M\cdot N\cdot D_F\cdot D_F}$$
$$=\frac{D_K^2\cdot M\cdot D_F^2+M\cdot N\cdot D_F^2}{D_K^2\cdot M\cdot N\cdot D_F^2}=\frac{(D_K^2+N)\cdot M\cdot D_F^2}{D_K^2\cdot N\cdot M\cdot D_F^2}$$
$$=\frac{D_K^2+N}{D_K^2\cdot N}=\frac{D_K^2}{D_K^2\cdot N}+\frac{N}{D_K^2\cdot N}=\frac{1}{N}+\frac{1}{D_K^2}$$

如果使用的卷积核都是3×3卷积核，那么深度可分离卷积的计算量是标准卷积的$(\frac{1}{N}+\frac{1}{9})$倍，也就是说使用深度可分离卷积能减少8到9倍的计算量，代价是损失一点准确度。

3.层结构与模型结构

上图左边的是标准卷积层：
使用的是3×3卷积Conv，加上批量归一化Batch Normalization，加上激活函数ReLU

上图右边的是深度可分离卷积层：
使用的是3×3深度卷积DW Conv，加上批量归一化Batch Normalization，加上激活函数ReLU。接着是1×1逐点卷积PW Conv(实际上就是标准的1×1卷积)，同样加上批量归一化Batch Normalization和激活函数ReLU。

input size：表示输入数据或者说是上一层的输出数据。
filter shape：表示卷积核形状，也就是卷积核的大小与数量，比如标准卷积的是H×W×M×N，深度卷积的是H×W×M dw。
Conv：表示标准卷积，如果filter shape中的是3×3×M×N就是3×3标准卷积，1×1×M×N就是1×1标准卷积也就是逐点卷积。
Conv dw：表示深度卷积，对应3×3×M dw。
stride：s1表示步长为1，特征图宽高不变。s2表示步长为2，特征图宽高减半。
avgpool：空间维度压缩，生成类别概率向量。
FC：表示全连接层，该层的每个神经元与前一层的所有神经元相连，实现全局特征的整合与映射，常作为分类器或回归器使用。
softmax：输出预测结果。

总的来说使用了1个标准卷积和13个深度可分离卷积进行串行学习。

4.宽度因子$\alpha$(Width multiplier )

在Mobilenet v1中除了使用深度可分离卷积来压缩模型大小外，还参考SqueezeNet模型引进了控制模型大小的超参数：宽度因子$\alpha$(Width multiplier )，用于控制输入和输出的通道数，即输入通道从M MM变为$\alpha M$,输出通道从N变为$\alpha N$。其中可设置$\alpha \in (0,1]$，通常取1 , 0.75 , 0.5 和 0.25，将计算量和参数降低了约${\alpha }^2$倍，可很方便的控制模型大小。

$$\frac{D_K\cdot D_K\cdot \alpha M\cdot D_F\cdot D_F+\alpha M\cdot \alpha N\cdot D_F\cdot D_F}{D_K\cdot D_K\cdot M\cdot N\cdot D_F\cdot D_F}=\frac{\alpha }{N}+\frac{{\alpha }^2}{D_K^2}$$

5.分辨率因子$\rho$(resolution multiplier )

除了宽度因子$\alpha$还引入了控制模型大小的超参数是：分辨率因子$rho$(resolution multiplier )，用于控制根源性输入和内部层的计算量。其中可设置输入分辨率$\rho$为224，192，160和128，将计算量和参数降低了约${\rho }^2$倍，可很方便的控制模型大小

$$\frac{D_K\cdot D_K\cdot M\cdot \rho D_F\cdot \rho D_F+M\cdot N\cdot \rho D_F\cdot \rho D_F}{D_K\cdot D_K\cdot M\cdot N\cdot D_F\cdot D_F}=\frac{\rho }{N}+\frac{{\rho }^2}{D_K^2}$$

结合两个超参数一起使用，那么计算量和参数可以降低了约${\alpha }^2{\rho }^2$倍

$$\frac{D_K\cdot D_K\cdot \alpha M\cdot \rho D_F\cdot \rho D_F+\alpha M\cdot \alpha N\cdot \rho D_F\cdot \rho D_F}{D_K\cdot D_K\cdot M\cdot N\cdot D_F\cdot D_F}=\frac{\alpha \rho }{N}+\frac{{\alpha }^2{\rho }^2}{D_K^2}$$

2、Mobilenet v2

Mobilenet v2论文地址

1.残差结构Residual Block

resnet论文地址

残差模块（Residual Block）是ResNet深度卷积神经网络的基本构建单元。它通过引入快捷连接（跳跃连接）机制解决了深度神经网络中的梯度消失问题，从而使得更深层次的网络可以有效地训练。残差模块的核心思想是学习输入和输出之间的残差函数，而不是直接学习输入到输出的映射，这样可以让网络更容易优化。

一个典型的残差模块包含两条路径：
主路径（主分支）：
通过多个卷积层、批归一化层和非线性激活函数来提取特征。

快捷连接（残差分支）：
将输入直接连接到输出，从而实现残差学习。

在ResNet深度卷积神经网络中有两种常用的残差结构：
左图：基础残差块 (Basic Block)​
第一层（3x3卷积）：​​ 通道数保持 64→ 接 ​​ReLU激活​。
​​第二层（3x3卷积）：​​ 通道数保持 64→ 接 ​​ReLU激活​。
​​跳跃连接（Shortcut）：输入特征​​直接​​与核心路径输出相加，要求输入与输出维度相同。
特点：适用于浅层网络（如ResNet-18/34），无维度变化操作，计算量较小，保留原始信息的同时学习残差。

右图：瓶颈残差块 (Bottleneck Block)
第一层（1x1卷积）：​​ 1x1 卷积将通道数从 256降维4倍至 64→ 接 ​​ReLU激活​。
​​第二层（3x3卷积）：​​ 通道数保持 64→ 接 ​​ReLU激活​。
​​第三层（1x1卷积）：​​ 1x1 卷积将通道数从 64升维4倍至 256→ 接 ​​ReLU激活​。
​​跳跃连接（Shortcut）：输入特征​​直接​​与核心路径输出相加，要求输入与输出维度相同。
特点​​：设计用于深层网络（如ResNet-50/101/152），通过​​先降维再升维​​减少参数量和计算量，中间3x3卷积在低维度下计算，效率更高。

2.倒置残差结构Inverted Residuals Block

倒置残差模块（Inverted Residuals Block）是MobileNet V2高效卷积神经网络基于瓶颈残差模块提出的一种构建单元。它的核心作用是​​保证模型在维持低 FLOPs 和低参数量的前提下，显著提升模型的表达能力​​，使得轻量级网络也能达到不错的精度。

左图：瓶颈残差块
第一层（1x1卷积）：​​ 1x1 标准卷积将通道数从256降维4倍至 64→ 接 ​​ReLU激活​。
​​第二层（3x3卷积）：​​ 3x3 标准卷积数保持 64→ 接 ​​ReLU激活​。
​​第三层（1x1卷积）：​​ 1x1 标准卷积将通道数从64升维4倍至256→ 接 ​​ReLU激活​。
​​跳跃连接（Shortcut）：输入特征​​直接​​与核心路径输出相加，要求输入与输出维度相同。
特点​​：​"降维→特征提取→升维"​​ 的维度变化顺序，跳跃连接确保网络能学习​​残差 而非完整映射，提升训练稳定性。

右图：倒置瓶颈残差块
第一层（1x1卷积）：1x1 标准卷积将通道数从64升维4倍至256→ 接 ​​ReLU6激活​。
​​第二层（3x3卷积）：3x3 DW卷积，stride=1，通道数保持 256→ 接 ​​ReLU6激活​。
​​第三层（1x1卷积）：1x1 PW卷积将通道数从256降维4倍至 64→ 接 ​​Linear激活​。
​​跳跃连接（Shortcut）：输入特征​​直接​​与核心路径输出相加，要求输入与输出维度相同。
特点​​：​"升维→特征提取→降维"​​ 的维度变化顺序，极大地增强了 Depthwise Conv 的特征提取能力​​，克服了其在低维空间的表达瓶颈。线性瓶颈和条件性残差连接确保特征信息有效流动且不被破坏。在提升轻量级模型精度的同时​​，还能几乎不增加额外计算负担。

3.Linear、ReLU和ReLU6激活函数

$$Linear(x)=x$$
对于Linear激活函数，输出值跟输入值一样。
​​优点:​​
​​计算极其简单：​​ 仅仅返回输入本身，是所有激活函数中最简单的，计算开销为零。在需要快速计算的简单模型中可能有轻微优势。
​​无梯度消失/爆炸问题（理论上）：​​ 导数为常数1，梯度在反向传播时不会放大或缩小（前提是整个网络都是线性的）。
​​可解释性：​​ 输出直接是输入的线性缩放，关系清晰。
​​缺点:​​
​​关键缺陷：无法引入非线性！​​ 这是致命的缺点。深度神经网络之所以强大，就在于能够组合和逼近复杂的非线性函数。无论堆叠多少层线性激活函数，整个网络仍然等价于​​单层​​线性变换（W_total * x + b_total），表达能力极其有限，无法学习复杂模式。
​​表达能力受限：​​ 只能解决线性可分的问题（如简单的线性回归），对于图像识别、自然语言处理等复杂非线性任务完全无能为力。

$$ReLU(x)=max(0,x)$$
对于ReLU激活函数，当输入值小于0的时候，默认都将它置0。当输入值大于0的时候，输出值跟输入值一样，不做处理。
优点:​​
​​高效计算：​​ 计算只涉及一次 max 操作，比 Sigmoid/Tanh 中的指数运算快得多，这是其在深度学习中普及的关键原因之一。
​​缓解梯度消失：​​ 在输入 x > 0的区域，导数恒为1，梯度可以无衰减地通过，有效解决了 Sigmoid/Tanh 等函数在深层网络中梯度消失严重的问题。
​​鼓励稀疏激活：​​ 大约 50% 的神经元（对于输入为负的）输出恒为零。这模拟了生物神经元的选择性激活特性，可能提高网络的表征效率（仅使用部分神经元识别特定特征），并引入了一定的正则化效果。
​​广泛流行与验证：​​ 作为深度学习革命的基石之一，ReLU 及其变体在大量任务和网络结构（尤其是 CNN）中被证明效果非常好，通常被当作首选的默认激活函数。
​​缺点:​​
​​Dying ReLU Problem (神经元死亡问题)：​​ 这是最严重的缺点。如果一个神经元的输出在大多数训练数据点上都为负（即大部分输入都小于0），那么它的梯度将恒为0，权重永远不会更新。这个神经元就永久性地“死亡”了，不再对学习过程产生贡献，相当于网络失去了一部分容量。
​​输出范围无上限：​​ 当输入为正时，输出可以非常大，在训练初期或遇到异常输入时可能导致数值不稳定。
​​非零中心化：​​ 输出范围 [0, +∞)，不以零为中心，可能导致梯度更新在特定方向上有偏向。

$$ReLU6(x)=min(max(0,x),6)$$
对于ReLU6激活函数，当输入值小于0的时候，默认都将它置0。在[0,6]区间内，不会改变它的输入值，但是当输入值大于6的时候，就会将输出值置为6。
优点:​​
​​高效计算：​​ 计算量比 ReLU 略大（多一次 min 比较），但依然远比 Sigmoid/Tanh 高效。
​​缓解梯度消失：​​ 在输入 0 <= x <= 6的区域，导数恒为1。
​​鼓励稀疏激活：​​ 输入小于0时输出为零，与 ReLU 相同。
​​缓解 Dying ReLU (间接)：​​ 通过限制上界，在某种程度上（虽然不直接针对原因）可能减轻训练不稳定性，间接影响导致神经元死亡的情况。
​​核心优势：控制正区间输出范围！​​ 将正区间的输出限制在 [0, 6]，这在以下场景极其关键：
​​量化友好性：​​ 这是 ReLU6 被设计的​​主要目的​​。在移动端、嵌入式设备等需要将浮点模型转换为低精度（如 int8）模型的场景中，已知的上限（6）使得量化参数的确定（缩放因子、零点）更加简单和鲁棒，显著降低量化损失，提高部署效率。
​​提高数值稳定性：​​ 避免了输入过大导致的潜在数值溢出问题。
​​学习更鲁棒的特征：​​ 限制特征值范围可能有助于模型学习对输入尺度变化不敏感的、更具鲁棒性的特征。
​​缺点:​​
​​牺牲了一些表达能力：​​ 人为设定了输出上限（6），可能会限制模型在某些情况下拟合极大正数值的能力（虽然现实中很多特征值本身有自然的上限）。这通常是模型设计时可控的权衡。
​​计算略复杂于 ReLU：​​ 多一次 min 操作。
​​Dying ReLU 问题依然存在：​​ 虽然输出上界被限制，但对于负输入导致的神经元死亡问题依然存在，并未从根本上解决。

使用标准的 ReLU，在量化过程中，非常大的激活值会“挤占”用于表示较小值的量化范围，导致小数部分的量化精度急剧下降，严重影响模型在低精度下的性能。ReLU6 将激活值上限强行限制在 6，​​强制限定​​了激活值的​​动态范围​​（[0, 6]）。

深度可分离卷积的参数少容量小，如果扩展层中使用标准的 ReLU，过大的激活值在被压缩层处理时，可能会被“粗暴”地投影到低维空间，破坏或过度扭曲原始的低维特征结构。通过限制激活值的最大幅度，能够减轻压缩层线性投影的压力，允许​​高维空间保留更丰富的信息​​扩展到更多通道，同时​​避免单个通道的极端值在压缩时过度扭曲低维特征​​。这有助于在复杂的特征提取（高维）和高效的表示（低维）之间取得更好的平衡。

固定的、有限的激活值范围使得后续的量化步骤变得​​更简单、更稳定​​，能更均匀地分配量化区间，保留更多有效信息，从而在量化后获得更好的精度​​。

4.线性瓶颈Linear Bottlenecks

MobileNet V2 引入的 ​​Linear Bottleneck（线性瓶颈）​​ 是一个关键创新点，与 Inverted Residuals（倒残差）结构紧密结合，旨在解决低维空间中深度卷积应用 ReLU 激活函数导致信息损失的问题，从而显著提高模型的效率和准确率。

图中Input代表一个嵌入在二维空间的、螺旋结构的特征矩阵，类比神经网络中某一层的输入特征，在本质上是低维且有结构的。

使用随机​​矩阵T（卷积核）映射升维到N维空间 (n = 2, 3, 5, 15, 30)，模拟神经网络中通过卷积核将输入特征从低维通道数M映射到高维通道数N，在N维空间中会应用​​ReLU​​或者ReLU6激活函数处理输出信息​​。应用随机​​矩阵T的逆矩阵$T^{-1}$将激活后的N维数据投影降维回二维空间，目的是为了​​可视化​​经过卷积+ReLU后的数据在原始低维空间中的变化，并非神经网络中的必要处理。

当输出维度N只有2层或者3层时，观察投影的输出数据，发现螺旋结构被严重截断破坏​​，大部分区域​​坍缩重叠在​​在同一点上（通常是原点附近），丢失了大量原始信息。这是因为原始输入数据升维后的空间维度本身不够高，数据在随机​​矩阵T映射升维的空间中部分可能会跨越ReLU的零点，也就是这些负值点被ReLU强制归零。导致表达不同信息的负值数据全部丢失信息，所以$T^{-1}$无法区分它们，使得它们在降维映射中全都坍缩到同一个点上。这就是所谓的信息丢失（Information Loss）或流形坍缩（Manifold Collapse）​​。

当输出维度N增加到5层时，观察投影的这5层输出数据，会发现坍缩现象相较减轻，但螺旋结构仍然有​​明显的扭曲断裂与小部分信息丢失​​。升维维度N的加深，使得输入数据中的某个值在随机​​矩阵T的映射下有了更丰富的表达，不再拘泥于负值，不会轻易被ReLU零点全部抹除或截断，但是维度​​仍然不够高​​，不足以避免重要信息的破坏和变形。

当输出维度N达到15层或者30层时，观察投影的输出数据，会发现螺旋结构​​基本得以完整保留​​，没有明显的点坍缩或大范围断裂。然而随着升维维度N的加深，螺旋形状发生了​​复杂的高度非线性的变形，不再是光滑有序的螺旋线，螺旋结构变得扭曲，部分数据表达更稀疏或者稠密。升维维度N的加深，为高维空间提供了充足的“空间”，使得输入的特征矩阵中每个数据都得到了丰富的表达，其大部分数据都有正值表达，从而能够避开ReLU的零点限制，展现出一个 ​​高度非凸（Highly Non-Convex）​​ 但 ​​结构完整（Structure Preserved）​​ 的形状。

5.层结构与模型结构

​​在紧接降维操作之后直接使用ReLU是危险的，在MobileNetV1和类似模型中，如果深度可分离卷积块的输入通道/输出通道维度不够高，ReLU 可能会导致严重的信息丢失坍缩，破坏流形结构和特征信息，导致部分训练参数归零。所以MobileNetV2不再在降维的瓶颈层使用ReLU或者ReLU6激活函数。

左图：带跳跃连接的倒置瓶颈残差块
第一层（1x1卷积）：1x1 标准卷积，通道数升维，使用​​ReLU6激活​。
​​第二层（3x3卷积）：3x3 DW卷积，stride=1，通道数保持不变，使用ReLU6激活​。
​​第三层（1x1卷积）：1x1 PW卷积，通道数降维，使用​​Linear激活​。
​​跳跃连接（Shortcut）：输入特征​​直接​​与核心路径输出相加，要求输入与输出维度相同。

右图：无跳跃连接的倒置瓶颈残差块
第一层（1x1卷积）：1x1 标准卷积，通道数升维，使用​​ReLU6激活​。
​​第二层（3x3卷积）：3x3 DW卷积，stride=2，通道数保持不变，使用ReLU6激活​。
​​第三层（1x1卷积）：1x1 PW卷积，通道数降维，使用​​Linear激活​。
​​无跳跃连接（Shortcut）：输入与输出的H×W×C不相同，不能相加。

input：表示输入数据或者说是上一层的输出数据，表示H×W×C。
operator：表示使用的神经网络层。
t：表示倒置残差结构中的扩展倍率。
c：表示输出特征矩阵的通道数。
n：表示对应神经网络层重复次数。
s：表示步长，会影响特征矩阵的宽高。在同一operator的重复的bottleneck中，s步长只代表第一个bottleneck的步长，剩下的bottleneck的步长为1。

3、Mobilenet v3

Mobilenet v3论文地址

1.激活函数优化

$$sigmoid(x)=\frac{1}{1+ex{p}^{-x}}$$

输出范围:
当x → -∞时，输出趋近 0。
当x → +∞时，输出趋近 1。
当x = 0时，输出为 0.5。

优缺点：
sigmoid激活函数具有非线性，能够赋予神经网络强大的拟合能力，输出具有概率意义，介于0-1之间，能用于二分类输出层。​​
但是sigmoid激活函数也具有饱和性问题、非零中心输出问题和计算复杂度高的问题。

$$ReLU6(x)=min(max(0,x),6)$$
$$hard\_sigmoid(x)=\frac{min(max(0,x+3),6)}{6}=\frac{ReLU6(x+3)}{6}$$

输出范围:
当 x ≤ -3时，输出为 0（因 sigmoid(-3) ≈ 0.047，可近似为 0）。
当 x ≥ 3时，输出为 1（因 sigmoid(3) ≈ 0.952，可近似为 1）。
当 -3 < x < 3时，设计线性函数需满足x = -3时输出 0，x = 3时输出 1，斜率为 (1 - 0)/(3 - (-3)) = 1/6。

优缺点：
hard_sigmoid激活函数计算速度快，仅使用加法、乘法和比较操作，​​避免了昂贵的指数运算​​，在CPU/GPU上计算效率显著高于Sigmoid，更容易被加速和在专用硬件上实现。
hard_sigmoid激活函数的输出近似Sigmoid，输出范围也是(0, 1)或一个非常接近的子集。​​
hard_sigmoid激活函数虽然是Sigmoid的​​分段线性近似​​，但是没有Sigmoid曲线那样平滑而且精度较差。
hard_sigmoid激活函数虽然梯度计算更快，但仍存在​​饱和性问题，没有解决梯度消失的根本问题。
hard_sigmoid激活函数的非零中心问题依然存在。​

$$swish(x)=x\cdot \sigma (x)=x\cdot \frac{1}{1+ex{p}^{-x}}$$

输出范围:
当x → -∞时，输出趋近 0。
当x → +∞时，输出趋近 +∞。
当x = 0时，输出为 0。

优缺点：
无上界​​有下界，当输入x趋近于正无穷时，输出趋近于正无穷，当输入x趋近于负无穷时，输出趋近于0。
swish激活函数曲线是平滑的，在x > 0区间是单调递减，在x < 0的部分​​不是​​单调的，存在一个极小值点。这一特性被认为有助于增强表达能力。
swish激活函数昂贵的​​指数运算​​，计算开销显著高于ReLU或其硬版本，接近Sigmoid。
swish激活函数的饱和性问题未完全解决，虽然在x < 0时梯度不会完全消失，但当x趋近负无穷大时会趋近于0，​​梯度仍然会变得非常微弱​​，但相比Sigmoid改善很多。

$$hard\_swish(x)=x\cdot \frac{ReLU6(x+3)}{6}$$

输出范围:
当 x ≤ -3时，输出为 0。
当x ≥ 3时，输出为 x。
当 -3 < x < 3时，输出为$\frac{x\cdot (x+3)}{6}$。

优缺点：
hard_swish激活函数核心操作是ReLU6，本质也是min、max和加法，​​避免了指数运算​​，运算速度快，对硬件友好，比Swish快得多。
​​hard_swish激活函数的曲线近似Swish曲线。
hard_swish激活函数的曲精度不如原始Swish。
hard_swish激活函数在近似分段点（x ≈ -3 和 x ≈ 3）处，函数虽然连续但其导数​​不连续​​。这在理论上不是最优，但在实际应用中影响常被容忍。
hard_swish激活函数在负区间存在饱和性问题。

使用 ​​hard_sigmoid​​ 替换了SE模块​​中的 ​​sigmoid​​ 和 ​​swish​​ 激活函数。
sigmoid 涉及指数运算，计算成本高，尤其在移动端硬件上，而hard_sigmoid 通过分段线性近似实现，仅需加减和乘法，显著降低计算量。
hard_sigmoid 的输出范围固定为 [0, 6]，更易适配定点量化（如 INT8），减少精度损失。

使用 ​​hard_swish​​ 替换了倒残差模块非线性激活层中的部分 ReLU6 和全部 swish 函数，仅在深层使用 hard_swish，浅层仍保留 ReLU6。
swish 依赖 sigmoid，导致求导和推理开销大，而 hard_swish 通过 ReLU6 近似 sigmoid，大幅简化计算流程。
swish 在深层网络中能提升特征表达能力，但硬件支持差。hard_swish 在精度损失极小的前提下，将推理速度提升 15–20%。

2.标准SE模块

SE模块论文地址
SE(Squeeze-and-Excitation)模块可以显式地建模卷积特征通道之间的相互依赖性来提高网络的表示能力，使得网络能够执行特征重新校准，通过这种机制可以学习使用全局信息来选择性地强调信息特征并抑制不太有用的特征。

特征图X：$H^{\prime }\times W^{\prime }\times C^{\prime }$，宽×高×深度。
特征图U：$H\times W\times C$，宽×高×深度。
特征图$\tilde{X}$：$H\times W\times C$，宽×高×深度。
$F_{tr}$：特征图转换函数，使用一个卷积核对特征图X进行卷积操作得到特征图U。
$F_{sq}$：特征图压缩函数，使用全局平均池化将特征图的全局信息嵌入压缩到一维特征向量。
$F_{ex}$：自适应权重函数，使用两个全连接层进行自适应校正通道权重。
$F_{scale}$：特征图加权函数，通道权重应用到特征图上。

$$u_c=F_{tr}(X)=v_c\ast X=\sum _{s=1}^{C^{\prime }}{v}_c^s\ast X^s$$

$u_c$：输出特征图U的第c个通道的二维特征矩阵。
$v_c$：用于生成特征图U的第 c个通道的二维特征矩阵的卷积核。
$v_c^s$：$v_c$在输入X的第s个通道上的权重切片。

$F_{tr}$是一个标准的卷积操作，通过输入的特征图和卷积核计算得到新的特征图，宽高不变，但深度可能会发生变化。

$$z_c=F_{sq}(u_c)=\frac{1}{H\times W}\sum _{i=1}^H\sum _{j=1}^W{u}_c(i,j)$$

$z_c$：一维向量z的第c个元素。
i, j：特征图U的第c个通道在空间位置 (i, j)处的值。

$F_{sq}$是一个特征图压缩函数，使用​​全局平均池化将特征图中每个通道的二维特征矩阵压缩​​成一个标量值，表示在该通道上的全局信息的激活强度，最终压缩得到的向量z尺寸为$1\times 1\times C$，向量的长度C对应特征图的深度C。

$$s=F_{ex}(z,W)=\sigma (g(z,W))=\sigma (W_2\delta (W_{1}z))$$

s： 通道注意力向量，重要性分数，值越大越重要。
z：输入的一维向量。
W：W1和 W2的统称，W1为第一个全连接层的权重矩阵 (C × C/r)，W2为第二个全连接层的权重矩阵 (C/r × C)。
r：约简率，控制瓶颈层的压缩程度，是SE模块需要调优的超参数，作用是减少模型复杂度和参数。
$\delta$：ReLU激活函数，为第一个全连接层提供非线性。
$\sigma$：Sigmoid 激活函数，将第二个全连接层的输出值映射到 [0, 1]区间，表示学习到的每个通道的自适应权重。

$F_{ex}$是一个自适应权重函数，由一个两个全连接层网络完成，第一个全连接层把C个通道压缩成了C/r个通道来降低计算量，再通过一个RELU非线性激活层，第二个全连接层将通道数恢复回为C个通道，再通过Sigmoid激活得到权重s，最后得到的这个s的维度是1×1×C，它是用来刻画特征图U中C个特征图的权重。
一个全连接层无法同时应用relu和sigmoid两个非线性函数，但是两者又缺一不可，所以先缩小，再放大，同时为了减少参数，设置了r比率。

$${\tilde{x}}_c=F_{scale}(u_c,s_c)=s_c{u}_c$$

${\tilde{x}}_c$: 特征图${\tilde{x}}_c$中第c个通道的特征矩阵。
$u_c$: 特征图U中第c个通道的特征矩阵。
$s_c$: 通道注意力向量s的第c个元素值。

$F_{scale}$是一个特征图加权函数，​​使用逐通道乘法​将学习到的通道权重s映射到特征图U上，也就是将自适应权重向量s的第c个元素值乘以特征图U的第c个特征矩阵的每一个元素。

3.MobieNetV3的SE模块

在mobilenet v2中，使用的是倒置残差结构Inverted Residuals Block和ReLU6、Linear激活函数，核心作用是​​保证模型在维持低 FLOPs 和低参数量的前提下，显著提升模型的表达能力​​，使得轻量级网络也能达到不错的精度。

第一个特征图→第二个特征图：使用 1×1 标准卷积核对第一个特征图的通道数进行升维，再使用ReLU6函数进行非线性激活。
第二个特征图→第三个特征图：使用 3×3 DW卷积核对第二个特征图进行学习，stride=1，使用NL非线性激活(​​h-swish)。
第三个特征图→Pool操作：使用全局平均池化把空间信息压缩为一维特征向量。
Poo操作→FC + ReLU操作：使用一个全连接层进行通道压缩来降低计算量，再使用ReLU6函数进行非线性激活。
FC + ReLU操作→FC + ​​hard-sigmoid​​操作：使用一个全连接层将通道数恢复回为C个通道，再通过hard-sigmoid函数得到特征图权重。
FC + ​​hard-sigmoid操作→第四个特征图​：​​使用逐通道乘法$⨂$将自适应权重向量s的第c个元素值乘以特征图U的第c个特征矩阵的每一个元素。
第四个特征图→第五个特征图：使用 1×1 PW卷积核对第四个特征图的通道数进行降维，stride=1，使用NL非线性激活(​​h-swish)。
​​跳跃连接：输入特征​​直接​​与核心路径输出相加，要求输入与输出维度相同。

MobileNet V3引入SE注意力模块的核心目标是在保持轻量化设计的同时，显著提升模型的特征提取能力和分类精度。以下是具体原因及作用机制：
SE模块通过动态学习不同通道的重要性权重，使模型能够自适应地强化关键特征并抑制冗余信息。
首先对每个通道进行全局平均池化，将空间信息压缩为通道描述符。随后通过全连接层学习通道间的依赖关系，最终用学习到的权重对原始特征图进行缩放。这一过程使模型能够捕捉全局上下文信息，弥补了轻量级模型因参数减少导致的感受野局限。
SE模块虽然增加少量参数（通常为输入通道数的1/4），但只在部分关键层（如深层或大卷积核层）加入SE模块，避免在所有层使用以控制计算量，却带来显著的精度提升。
深度可分离卷积虽然减少参数量，但该操作可能导致通道间信息交互不足，SE模块通过重标定通道权重，强化了通道间的关联性，弥补了分离卷积的不足。
深度可分离卷积压缩通道数使得低维特征易受ReLU等激活函数的信息损失影响，SE模块通过特征重加权，使低维特征也能保留关键信息。
SE模块的计算主要由全局池化和全连接层构成，易于在移动端硬件上并行优化，实际部署时延迟增加可控。

4.精简模型结构

移除了原始末阶段中完整的 ​​3×3 DConv+ BN + H-Swish激活​​模块。
深度可分离卷积虽然比标准卷积高效，但在靠近网络尾端的特征图尺寸已经很小的情况下，其相对于1x1卷积的计算量优势减弱，且同样带有显著的计算开销。

​​删除最后的 ​​1×1 Conv + BN​​ 层。
从原来将320通道升维到1280通道的卷积操作，修改为将960通道直接通过avgpool + 1×1 Conv + H-Swish激活​​模块升维到1280通道。使得最后阶段的数据流更短、更直接，还极大地降低了后续卷积的计算量，同时​​基本保持了模型的精度。

更新网络后准确率是几乎没有变化的，但是节省了7ms的执行时间。这7ms占据了推理11%的时间，因此使用Efficient Last Stage取代Original Last Stage对速度提升还是比较明显的。

5.层结构与模型结构

​​Large模型

Small模型

input：表示输入数据或者说是上一层的输出数据，表示H×W×C。
operator：表示使用的神经网络层，​​混合使用3×3 和 5×5尺寸的卷积核。
exp size：表示在深度可分离卷积结构中​​使用逐点卷积进行升维的中间通道数​​。
#out：​​表示当前层输出的特征图通道数​​。
SE：表示是否启用通道注意力机制​​，✓表示启用。
NL：表示使用的非线性激活函数类型​​。
s：表示步长，会影响特征矩阵的宽高。在同一operator的重复的bottleneck中，s步长只代表第一个bottleneck的步长，剩下的bottleneck的步长为1。
NBN：表示这卷积不使用BN结构，最后两个卷积相conv2d 1x1当于全连接的作用。

​​MobileNetV3-Large:​​ ​​优先保证精度​​。为此采用了更深、更宽（更多通道、更大扩展因子）的网络结构，在更多瓶颈块中部署SE模块，并主要在深层使用计算量更高的Hard Swish激活函数。

​​MobileNetV3-Small:​​ ​​优先追求极致的速度和效率​​。为此网络设计得更浅、通道数更低、扩展因子更小、精简SE模块的使用、并在早期和中期更多地使用计算量较低的HS激活函数。

4、Mobilenet v4

Mobilenet v4论文地址

1.通用倒置瓶颈Universal Inverted Bottleneck

通用倒置瓶颈UIB是​​一个统一、灵活的基础模块架构​​，适用于高效网络设计的可适应构建块，它具有灵活地适应各种优化目标的能力，而不会使搜索复杂度爆炸性增长。

UIB结构
第一层：可选的DW卷积
第二层：升维的PW卷积
第三层：可选的DW卷积
第四层：降维的PW卷积

Extra DW结构
第一层：DW卷积
第二层：升维的PW卷积
第三层：DW卷积
第四层：降维的PW卷积

MobileNet Inverted Bottleneck结构
第一层：无
第二层：升维的PW卷积
第三层：DW卷积
第四层：降维的PW卷积

ConvNext-Like结构
第一层：DW卷积
第二层：升维的PW卷积
第三层：无
第四层：降维的PW卷积

ViT-FFN结构
第一层：无
第二层：升维的PW卷积
第三层：无
第四层：降维的PW卷积

通过​​开关可选DW层​​，UIB可转化为各种的常规模块。

Fused IB结构
第一层+第二层：融合的标准Conv2D卷积
第三层：无
第四层：降维的PW卷积

Fused IB 模块在UIB模块的基础上进行改进，融合了UIB模块中的预膨胀DW卷积和升维PW卷积，将空间滤波和通道滤波的功能融合到了一个标准的Conv2D操作中。
GPU的瓶颈常是内存带宽而非计算能力，而独立的DW卷积和PW卷积需多次读写中间特征图数据，导致高内存延迟。融合的DW和PW的连续计算合并为单次核函数，中间结果无需写入外部内存，​​访存量减少30%以上​​，在保持或提升模型表达能力的同时，减少计算量和延迟，使其在硬件上的运行更加高效。

2. 移动优化注意力机制Mobile MQA

Mobile MQA（Multi-Query Attention）​​ 是一种专为移动加速器优化的注意力机制，旨在显著提升推理速度同时保持模型精度。其核心设计结合了标准多查询注意力（MQA）​​ 和​​非对称空间下采样（Asymmetric Spatial Reduction）​​，以降低内存访问开销并提高操作强度。

标准多查询注意力的轻量化改进​​：
​​传统多头注意力MHA（Multi-Head Attention）对输入特征分别投影生成独立的 Query、Key、Value 矩阵，导致内存访问频繁，尤其在移动加速器上（计算能力强但内存带宽有限）成为性能瓶颈。
通过保留多组 Query 投影（每个注意力头独立），而 ​​Key 和 Value 在所有注意力头之间共享​​。这减少了约25%的参数量和内存访问量，同时实验表明对精度影响极小。

​​非对称空间下采样（Spatial Reduction, SR）​​：
混合模型中，早期卷积层已提取空间局部相关性，因此在注意力模块中对 Key/Value 进行下采样不会显著丢失信息。
对 Key 和 Value 进行空间下采样（步长为2的深度卷积 DWConv），​​保持 Query 的分辨率不变​​。
公式中的 SR(X)表示对输入特征图 X的空间缩减操作，通过步长为2的3 × 3深度可分离卷积替代AvgPooling实现，以低成本扩大感受野并减少计算量12。

$$Attention(Q,K,V)=softmax(\frac{Q{K}^T}{\sqrt{d_k}})V$$

$$whereattentio{n}_j=softmax\left(\frac{(X{W}^{Q_j})(SR(X)W^K{)}^T}{\sqrt{d_k}}\right)(SR(X)W^V)$$

$$MultiHead(Q,K,V)=Concat(hea{d}_1,...,hea{d}_h)W^O$$

$$Mobile\_MQA(X)=Concat(attentio{n}_1,...,attentio{n}_n)W^o$$

$X$：输入特征图
$Concat$：张量拼接，会扩充两个张量的维度。
$attentio{n}_j$：第j个注意力头。
$W^o$：多头输出的融合矩阵。
$softmax$：激活函数，将输出的分类结果映射到[0，1]之间。
$W^{Q_j}$：第 j个注意力头的 ​​Query 投影矩阵​。
$W^K$：共享的Key投影矩阵​。
$W^V$：共享的Value投影矩阵​。
$SR$：空间缩减函数，使用深度可分离卷积实现的非对称下采样。
$d_k$：Key 向量的维度。

输入X直接投影生成第j个头的Query，保持原始空间分辨率H×W，通过SR下采样投影生成共享的Key 和Value。然后参考原始Attention公式进行计算，得到在第j个位置上的注意力头输出。
在多头机制下，输入的序列数据会被分成多个头，每个头进行独立的计算，得到不同的输出。这些输出最后被拼接在一起，通过$W^o$融合为最终结果。

---

三、ShuffleNet

1、ShuffleNet V1

ShuffleNet V1论文地址

1.分组卷积Group Convolution

在分组卷积中，g = 1，$C_{in}=C_{out}$时：

相当于不分群组，所有输入通道都在​​一个组​​里，该组卷积核需要与所有输入通道进行卷积操作，来生成​​所有​​输出通道。这是分组卷积的一个极端且非常重要的特例，称为标准卷积​​。
虽然这样学习到的特征会充分混合，但是计算量和参数量却是最大的。

在分组卷积中，1 < g < $C_{in}$，$C_{in}=C_{out}$时：

将输入通道​​平均分成g组​​，每组有$\frac{C_{in}}{g}$个通道。
第一组包含 [通道1, 通道2,…, 通道$\frac{C_{in}}{g}$]
第二组包含 [通道$(\frac{C_{in}}{g}+1)$, 通道$(\frac{C_{in}}{g}+2)$,…, 通道$(\frac{C_{in}}{g}+\frac{C_{in}}{g})$]
…
第g组包含 [通道$(C_{in}-\frac{C_{in}}{g}+1)$, 通道$(C_{in}-\frac{C_{in}}{g}+2)$,…, 通道$C_{in}$]

第g组卷积核​​只与第g组进行卷积，生成第g组​​输出通道。​​最后将将不同组得到输出按顺序在通道维度上进行拼接，得到最终的输出特征图。
这样学习到的特征参数量和计算量减少，是标准卷积的$\frac{1}{g}$​​。

在分组卷积中，g = $C_{in}$，$C_{in}=C_{out}$时：

相当于每个输入通道都作为​​独立的一个组，一个卷积核只与一个输入通道进行卷积操作，来生成​​所有​​输出通道。将所有单通道的输出拼接起来，得到最终的输出特征图。这是分组卷积的一个极端且非常重要的特例，称为​​DW深度卷积​​。
这样学习到的特征参数量和计算量降到极低，是标准卷积的$\frac{1}{C_{in}}$

$$ConvolutionKernel=\frac{C_{in}\times C_{out}}{g}$$

g：分组数。
$C_{in}$：输入特征图深度，也就是通道数。
$C_{out}$：输出特征图深度，也就是通道数。

在分组卷积中，每个分组只在组内执行一个小的标准卷积，这使得模型的参数数量会减少。

如果一个卷积层有4个输入通道和4个输出通道，且不使用分组，那么将有4个输入通道× 4个输出通道=16个权重参数。

如果使用g=2进行分组卷积，每个分组将只有2个输入通道和2个输出通道，因此每组只有4个权重参数，两个分组总共8个参数，减少了一半的权重参数。

由于参数数量的减少，分组卷积在前向传播和反向传播过程中的计算量也会减少。这可以加快训练和推理的速度，尤其是在资源受限的情况下。

分组卷积可以提高计算的并行度，因为每个分组可以独立地进行计算。这使得分组卷积在多核处理器和GPU上更加高效。

减少参数和计算量也意味着节省了内存使用，这对于部署在内存受限的设备上的模型尤其重要。

2.通道混洗操作channel shuffle

a)标准分组卷积
将输入的特征图按通道顺序划分为红、绿、蓝三组，每组特征图使用GConv1分组卷积在​​组内​​进行独立计算，GConv1输出的Feature特征图同样按通道顺序保持着组间的隔离。下一层的GConv2分组卷积同样在​​组内​​进行独立计算，最后输出最终的output特征图。

虽然标准分组卷积极大减少了计算量和参数，但是特征​​信息流被限制在每个通道组内部，只能接收到来自自己组内的信息，组内特征之间只能进行有限学习，组外特征无法交流，容易导致模型学习到的特征非常局限，模型的性能和表达能力大打折扣。

b)交叉分组思路
将输入的特征图按通道顺序划分为红、绿、蓝三组，每组特征图使用GConv1分组卷积在​​组内​​进行独立计算，GConv1输出的Feature特征图同样按通道顺序保持着组间的隔离。下一层的GConv2分组卷积从Feature特征图的各个通道中交叉提取拼出新的特征分组，并进行独立计算，最后输出最终的output特征图。

实现了跨组的信息流动，让后续的卷积操作能够融合来自不同组的信息，大大提升了模型的表现力。

c)通道混洗分组卷积
将输入的特征图按通道顺序划分为红、绿、蓝三组，每组特征图使用GConv1分组卷积在​​组内​​进行独立计算，GConv1输出的Feature特征图同样按通道顺序保持着组间的隔离。使用Channel Shuffle操作将Feature特征图每个分组内部按组数均匀划分为三份子块，将原本属于不同组的通道混合起来并交错排列。下一层的GConv2分组卷积在​​新构建的分组内​​进行独立计算，最后输出最终的output特征图。

实现了与(b))交叉分组相同的思路，促进了通道组间的信息交流，让后续的卷积操作能够融合来自不同组的信息，大大提升了模型的表现力。
通道混洗”只是一个简单的张量变形重塑和索引排序操作，​​不涉及任何计算或需要学习的参数​​，因此计算成本几乎可以忽略不计。

3.层结构与模型结构

a)带深度可分离卷积的残差模块
​​1×1 Conv+BN ReLU：使用1×1普通卷积​​对输入的特征图进行通道​​升维，然后使用批归一化和ReLU激活函数。
3×3 DWConv+BN ReLU：使用3×3​​深度可分离卷积​​对输入的特征图进行空间特征学习，然后使用批归一化和ReLU激活函数。
1×1 Conv+BN：使用1x1普通卷积​​对输入的特征图进行通道​​降维，然后使用批归一化。
​​Add+ReLU​​：通过​​残差连接将旁路和主路的特征图相加，然后使用ReLU激活函数。

​​b)带有通道混洗分组卷积的残差模块
​​1×1 GConv+BN ReLU：使用1×1分组卷积​​对输入的特征图进行通道​​升维，然后使用批归一化和ReLU激活函数。
​​Channel Shuffle​​：​​通道混洗​​操作，通过重新排列通道的顺序，让后续的卷积操作能够接收到来自不同组的特征，促进了组间信息交换。
3×3 DWConv+BN：使用3×3​​深度可分离卷积​​对输入的特征图进行空间特征学习，然后使用批归一化和ReLU激活函数。
1×1 GConv+BN：使用1x1分组卷积​​对输入的特征图进行通道​​降维，然后使用批归一化。
​​Add+ReLU​​：通过​​残差连接将旁路和主路的特征图相加，然后使用ReLU激活函数。

c)带有通道混洗分组卷积的残差下采样模块
​​1×1 GConv+BN ReLU：使用1×1分组卷积​​对输入的特征图进行通道​​升维，然后使用批归一化和ReLU激活函数。
​​Channel Shuffle​​：​​通道混洗​​操作，通过重新排列通道的顺序，让后续的卷积操作能够接收到来自不同组的特征，促进了组间信息交换。
3×3 DWConv(stride=2)+BN：使用3×3​​深度可分离卷积​​对输入的特征图进行步长为2的空间特征学习，对特征图进行下采样操作，然后使用批归一化和ReLU激活函数。
1×1 GConv+BN：使用1x1分组卷积​​对输入的特征图进行通道​​降维，然后使用批归一化。
3×3 AVGPool(stride=2)：​​使用平均池化对特征图进行下采样，平均池化更关注区域的全局统计特征，适用于需要保留背景或平缓变化的场景。
​​Concat+ReLU​​：旁路和主路的特征图高度和宽度相同，但通道数不同​​，使用Concat操作将它们沿着通道维度直接拼接起来，最终输出特征图的通道数等于旁路和主路的通道数之和​​，然后使用ReLU激活函数。

$$Resnet:hw(1\times 1\times c\times m)+hw(3\times 3\times m\times m)+hw(1\times 1\times m\times c)=hw(2cm+9m^2)$$
$$ShuffleNet:hw(1\times 1\times c\times m)/g+hw(3\times 3\times m)+hw(1\times 1\times m\times c)/g=hw(2cm/g+9m)$$

对于Resnet结构，第一个是1×1标准卷积的计算量为$1\times 1\times w\times h\times c\times 1\times m$，第二个是3×3标准卷积的计算量为$3\times 3\times w\times h\times c\times m\times m$，第三个是1×1标准卷积的计算量为$1\times 1\times w\times h\times c\times 1\times m$。

对于ShuffleNet结构，第一个是1×1分组卷积的计算量为$(1\times 1\times w\times h\times c\times 1\times m)/g$，第二个是3×3DW卷积的计算量为$3\times 3\times w\times h\times c\times m$，第三个是1×1分组卷积的计算量为$(1\times 1\times w\times h\times c\times 1\times m)/g$。

Output size：输入特征图的W×H。
KSize：卷积核大小。
Stride：步长。
Repeat：每个Stage的重复次数。
Output channels(g groups)：在不同分组情况下的特征图通道数。

Image：图像输入大小为224×224。
Conv1：标准卷积，有效提取初始特征和通道升维。
MaxPool：最大池化下采样，进一步下采样，快速减少计算量较大的空间尺寸。
Stage2：核心构建模块，首先使用一个步长为2的带有通道混洗分组卷积的残差下采样模块对特征图进行下采样，然后使用三个步长为1的带有通道混洗分组卷积的残差模块对特征图进行学习。
Stage3：核心构建模块，首先使用一个步长为2的带有通道混洗分组卷积的残差下采样模块对特征图进行下采样，然后使用七个步长为1的带有通道混洗分组卷积的残差模块对特征图进行学习。
Stage4：核心构建模块，首先使用一个步长为2的带有通道混洗分组卷积的残差下采样模块对特征图进行下采样，然后使用三个步长为1的带有通道混洗分组卷积的残差模块对特征图进行学习。
GlobalPool： 7×7的全局平均池化，将最后一个Stage输出的7x7的特征图直接降维成1×1。
FC：全连接层，将GlobalPool后的向量映射到1000个类别上。
Complexity：模型复杂度分析。

当 g=1​​：所有通道都参与计算​​，即标准卷积。
当 g=2​​：输入和输出通道被分成2个独立的组​​，卷积操作在这两个组内分别进行，然后再将结果拼接起来。
…
当 g=8​​：输入和输出通道被分成8个独立的组​​，卷积操作在这八个组内分别进行，然后再将结果拼接起来。

ShuffleNet通过引入​​分组卷积​​来大幅降低计算量，分组数g越多，计算量就越小。

如果一味地增加分组，即使有​​Channel Shuffle机制​​促进组间信息交换，但是还是不可避免的导致学习能力下降。
增加分组能够节省计算量，使用省下来的计算量去增加通道数，从而使总计算量保持稳定​​。
同时为了公平地比较不同分组的模型性能，尽量使得不同分组的模型在​​相近的计算复杂度​​下进行对比。
因此，当增加分组g时，Stage2会选择​​增加通道数，Stage3和Stage4则通道翻倍，一方面通过增加深度加强学习能力，另一方面平衡不同分组模型的计算量。

2、ShuffleNet V2

ShuffleNet V2论文地址

1.MAC、MACs、FLOPs与FLOPS

$$a=a+(b\times c)$$
MAC：​​乘加运算Multiply-Accumulate Operation，主要包含一个乘法和一个加法，是神经网络中最常见、最基础的操作单元。

$$MACs=H\times W\times C_{in}\times K\times K\times C_{out}$$
MACs：乘加运算次数​Multiply–Accumulate Operations，是一个数量单位，用来衡量模型的计算复杂度或计算量。

$$FLOPs=2\times H\times W\times C_{in}\times K\times K\times C_{out}$$
​​FLOPs​​： 浮点运算次数Floating Point Operations，这是一个​​数量​​单位，用来衡量一个模型、一个算法或一次计算​​总共需要多少次浮点运算。​​1次MAC = 2次FLOPs​​（因为一次乘法算一次FLOP，一次加法也算一次FLOP）。

$$FLOPS=(总的浮点运算次数(FLOPs))/(计算所花费的时间(s))$$
​​FLOPS​​： 每秒浮点运算次数Floating Point Operations Per Second​​，这是一个​​速率​​单位，用来衡量计算硬件CPU或GPU​​每秒钟能执行多少次浮点运算​​，是衡量计算性能的指标。

2.高效网络设计指南

在GPU计算平台和ARM计算平台上，对比了ShuffleNet V1与MobileNet V2两种模型在推理运行时中不同操作的时间消耗占比：

Conv：​​卷积操作​​，是卷积神经网络中最核心也是最耗时的操作之一。
Data：数据IO，主要包括内存的读取、写入等操作，在计算能力强的硬件上，这部分开销会相对明显。
Elem-wise：逐元素操作，例如激活函数、张量乘加等操作，虽然计算量小但是次数频繁。
Shuffle：通道混洗操作​​，ShuffleNet模型特有的操作。
Other：其他操作​​。

在GPU中ShuffleNet V1的卷积占了一半的推理时间，其次是数据IO和逐元素操作也占据了较大的比例，剩下的就是其他操作与通道混洗操作​​。
在ARM中ShuffleNet V1的卷积占了绝大部分的推理时间，其次是其他操作和逐元素操作占据了小部分的比例，剩下的数据IO与通道混洗操作​​几乎可以忽略不计。
在GPU中MobileNet V2的卷积占了一半的推理时间，其次是数据IO和逐元素操作也占据了较大的比例，剩下的就是其他操作​​。
在ARM中MobileNet V2的卷积占了绝大部分的推理时间，其次是逐元素操作占据了小部分的比例，剩下的数据IO与其他操作​​几乎可以忽略不计。

不同模型在不同计算平台上的表现，体现了不同操作的在推理运行中的时间占比。
GPU具有强大的并行计算能力，而ARM的并行计算能力远弱于GPU，所以卷积操作的计算耗时占比相对会更多。
ARM属于一种CPU芯片，对于复杂串行的数据读取或写入操作会比GPU更加灵活与快捷，所以ARM的数据IO操作耗时会比GPU更少。
ShuffleNet对比MobileNet模型使用了分组卷积和通道混洗操作，导致在GPU和ARM上的Shuffle和Other的计算耗时占比相对更多。
所以一个模型在GPU上高效，并不意味着在ARM上也同样高效​​。不同的硬件架构对不同计算操作的优化程度不同，因此设计移动端模型时必须考虑目标平台的特性。

3.高效网络设计指南

G1）Equal channel width minimizes memory access cost (MAC)
相等的通道宽度最大限度地降低了内存访问成本（MAC）。
核心思想：​​ 在卷积运算中，当输入通道数$C_{in}$和输出通道数$C_{out}$相等时，内存访问成本最小，从而能实现更高的计算效率。这里的MAC指的是内存访问成本而不是上面的乘加运算单元。

在硬件计算中，对内存进行增删读写等访问操作所消耗的时间和能量往往比执行计算操作本身还要多，使用降低内存访问成本是优化速度的关键。

$$B=H\times W\times C_{in}\times K\times K\times C_{out}=HW{C}_{in}{C}_{out}$$
$$MAC=H\times W\times C_{in}+C_{in}\times C_{out}+H\times W\times C_{out}=HW(C_{in}+C_{out})+C_{in}{C}_{out}$$
$$\frac{a+b}{2}\ge \sqrt{a\times b}(当a=b时，均值不等式的两边相等)$$
$$MAC=HW(C_{in}+C_{out})+C_{in}{C}_{out}\ge H\times W\times 2\sqrt{C_{in}\times C_{out}}+C_{in}\times C_{out}\ge 2\sqrt{HWB}+\frac{B}{HW}$$

一个1×1卷积层的理论计算量B是通过FLOPs（看起来像是MACs）计算得到的，一个1×1卷积层的内存访问量MAC为输入张量的读取+卷积核权重的读取+输出张量的写入。

当固定计算预算B的前提下，根据均值不等式，当输入通道数$C_{in}$和输出通道数$C_{out}$相等时，内存访问量MAC取得最小值。如果输入通道数$C_{in}$和输出通道数$C_{out}$相差很大，内存访问量MAC就会显著增加。

所以在设计Bottleneck网络块时，要尽量让中间层的通道数与输入输出通道数保持相等或接近，而不是为了降低FLOPs而过度压缩中间通道数。​​看似FLOPs降低，但是内存访问量MAC可能很高，导致实际速度变慢。​​

G2）Excessive group convolution increases MAC
过多的分组卷积会增加MAC。
核心思想：​​ 分组卷积虽然能减少计算量FLOPs，但过度使用或分组数g过大会导致内存访问成本MAC急剧增加。

$$B=\frac{HW{C}_{in}{C}_{out}}{g}$$
$$MAC=HW{C}_{in}+HW{C}_{out}+C_{in}{C}_{out}=\frac{Bg}{c_{out}}+\frac{Bg}{c_{in}}+\frac{B}{HW}$$

一个1×1分组卷积层的理论计算量B是通过FLOPs（看起来像是MACs）计算得到的，当分组越多g值越大，B值会越小。

一个1×1分组卷积层的内存访问量MAC为输入张量的读取+卷积核权重的读取+输出张量的写入，当分组越多g值越大，卷积核权重的读取会越快。

ShuffleNet V1中当分组越多g值越大，通常需要增加通道数来保持模型学习量，这也导致$HW(C_{in}+C_{out})$实际上在g增加时通道数也会增加，导致内存访问成本MAC增加。

当B固定不变时，分组越多g值越大，会导致$\frac{Bg}{c_{out}}$和$\frac{Bg}{c_{in}}$增加。

虽然分组卷积在实际推理中非常节省计算，但是当使用的分组数越多g值越大反而可能会因为MAC的大幅增加而抵消掉FLOPs减少带来的好处，甚至让速度变慢。

G3）Network fragmentation reduces degree of parallelism
网络碎片降低了并行度。
核心思想：​​ 如果一个Bottleneck网络块中包含太多的小型操作或分支，显得网络结构过于“碎片化”，会导致硬件并行计算能力降低，即使它可能让理论FLOPs更低。

一个模块由多条不同路径分支组成，每个分支又可能包含一些1x1卷积、3x3卷积、池化等小操作，这些小操作的特点就是计算强度低、数据量小、操作简单。

在计算平台中这些操作都需要GPU内核来启动和执行，频繁启动多个小内核会产生额外开销。而分支结构需要在最终合并点进行同步，等待所有分支计算完成，这可能会造成等待和延迟。

尽管这种碎片化的结构已被证明对准确性有益，但它可能会降低效率，因为它对具有强大并行计算能力的GPU设备不友好。

一个纯粹的的卷积操作更容易被硬件优化和并行化，使得计算效率更高，所以在网络架构设计时，应倾向于更简单、更纯粹、更“稠密”的模块结构，减少分支数量，尤其是在需要高速度的轻量级网络中。

G4）Element-wise operations are non-negligible
元素操作是不可忽略的。
核心思想：​​逐元素操作虽然理论FLOPs很低，但其内存访问成本很高，在轻量级网络中会占用相当比例的运行时间。

元素级操作是指那些输入和输出张量在对应位置上的元素独立进行计算的操作。例如激活函数、逐元素加法、逐元素乘法等，它们的计算量小浮点运算数小，但它们需要读取和写入整个张量​​导致内存访问成本MAC相对较高。

在大型网络中，卷积等计算密集型操作占绝对主导，元素级操作的耗时占比不明显。但在轻量级网络中，FLOPs总量本来就少，这些操作的相对开销就变得非常突出。所以优化网络时，不能只盯着卷积的FLOPs，还需要尽量减少元素级操作的数量。可以移除一些不必要的激活函数，或者将连续的逐元素操作合并在一起执行，以减少内存读写次数。

总结：

1. 使用平衡的通道宽度相等的卷积操作。
2. 注意使用分组卷积的成本。
3. 降低模型碎片化操作的开销。
4. 减少不必要的元素级操作。

4.层结构与模型结构

​​a)带有通道混洗分组卷积的残差模块
​​1×1 GConv+BN ReLU：使用1×1分组卷积​​对输入的特征图进行通道​​升维，然后使用批归一化和ReLU激活函数。
​​Channel Shuffle​​：​​通道混洗​​操作，通过重新排列通道的顺序，让后续的卷积操作能够接收到来自不同组的特征，促进了组间信息交换。
3×3 DWConv+BN：使用3×3​​深度可分离卷积​​对输入的特征图进行空间特征学习，然后使用批归一化和ReLU激活函数。
1×1 GConv+BN：使用1x1分组卷积​​对输入的特征图进行通道​​降维，然后使用批归一化。
​​Add+ReLU​​：通过​​残差连接将旁路和主路的特征图相加，然后使用ReLU激活函数。

b)带有通道混洗分组卷积的残差下采样模块
​​1×1 GConv+BN ReLU：使用1×1分组卷积​​对输入的特征图进行通道​​升维，然后使用批归一化和ReLU激活函数。
​​Channel Shuffle​​：​​通道混洗​​操作，通过重新排列通道的顺序，让后续的卷积操作能够接收到来自不同组的特征，促进了组间信息交换。
3×3 DWConv(stride=2)+BN：使用3×3​​深度可分离卷积​​对输入的特征图进行步长为2的空间特征学习，对特征图进行下采样操作，然后使用批归一化和ReLU激活函数。
1×1 GConv+BN：使用1x1分组卷积​​对输入的特征图进行通道​​降维，然后使用批归一化。
3×3 AVGPool(stride=2)：​​使用平均池化对特征图进行下采样，平均池化更关注区域的全局统计特征，适用于需要保留背景或平缓变化的场景。
​​Concat+ReLU​​：旁路和主路的特征图高度和宽度相同，但通道数不同​​，使用Concat操作将它们沿着通道维度直接拼接起来，最终输出特征图的通道数等于旁路和主路的通道数之和​​，然后使用ReLU激活函数。

​​c)带有通道分割的深度可分离卷积残差模块
Channel Split：使用通道分割操作将输入在通道维度上被​​直接、无计算地​​切分成两部分。
​​1×1 Conv+BN ReLU：使用1×1卷积​​对输入的特征图进行通道​​升维，然后使用批归一化和ReLU激活函数。
3×3 DWConv+BN：使用3×3​​深度可分离卷积​​对输入的特征图进行空间特征学习，然后使用批归一化和ReLU激活函数。
1×1 Conv+BN ReLU：使用1x1分组卷积​​对输入的特征图进行通道​​降维，然后使用批归一化。
​​Concat：使用Concat操作将它们沿着通道维度直接拼接起来，最终输出特征图的通道数等于旁路和主路的通道数之和​​，使得输出通道数等于输入通道数。
​​Channel Shuffle​​：​​通道混洗​​操作，通过重新排列通道的顺序，对拼接后的结果进行通道混洗，促进左右分支的信息交流，为下一个单元做准备。

d)深度可分离卷积的残差下采样模块
左分支：
3×3 DWConv(stride=2)+BN：使用3×3​​深度可分离卷积​​对输入的特征图进行步长为2的空间特征学习，对特征图进行下采样操作，然后使用批归一化和ReLU激活函数。
1×1 Conv+BN ReLU：使用1x1分组卷积​​对输入的特征图进行通道​​降维，然后使用批归一化。

右分支：
​​1×1 Conv+BN ReLU：使用1×1卷积​​对输入的特征图进行通道​​升维，然后使用批归一化和ReLU激活函数。
3×3 DWConv(stride=2)+BN：使用3×3​​深度可分离卷积​​对输入的特征图进行步长为2的空间特征学习，对特征图进行下采样操作，然后使用批归一化和ReLU激活函数。
1×1 Conv+BN ReLU：使用1x1分组卷积​​对输入的特征图进行通道​​降维，然后使用批归一化。

合并：
​​Concat：使用Concat操作将它们沿着通道维度直接拼接起来，两个分支下采样输出的特征图尺寸相同，在通道维度上​​拼接起来，因此通道数翻倍。
​​Channel Shuffle​​：​​通道混洗​​操作，通过重新排列通道的顺序，对拼接后的结果进行通道混洗，促进左右分支的信息交流，为下一个单元做准备。

在c模型结构中：
通道分割操作将输入通道分成两个分支，一半原始特征数据用作残差保留，一半原始特征数据进行轻量计算，避免了碎片化操作。
左分支执行恒等映射，保持输入和输出通道数不变，降低模型碎片化操作的开销。
右分支执行多层卷积，将​​分组卷积替换为普通卷积​​，虽然没有降低FLOPs，但是避免了内存访问成本的增加。
使用Concat合并，相比Add加法具有更低的计算复杂度，如果使用Add加法操作融合特征在一定程度上会稀释原始的恒等信息，而Concat合并则完美保留了一半的原始输入信息。
最后输入和输出的通道数相等，实现通道宽度相等的卷积操作，能够最小化内存访问成本。

在d模型结构中：
左分支执行多层卷积，使用DW卷积和普通卷积进行下采样操作，虽然没有降低FLOPs，但是避免了内存访问成本的增加。
右分支执行多层卷积，使用深度可分离卷积进行下采样操作​​，虽然没有降低FLOPs，但是避免了内存访问成本的增加。
两个分支的结构相似对称，都包含了实际计算的操作，有利于提高并行度。

Output size：输入特征图的W×H。
KSize：卷积核大小。
Stride：步长。
Repeat：每个Stage的重复次数。
Output channels：在不同复杂度系数下的特征图通道数。

Image：图像输入大小为224×224。
Conv1：标准卷积，有效提取初始特征和通道升维。
MaxPool：最大池化下采样，进一步下采样，快速减少计算量较大的空间尺寸。
Stage2：核心构建模块，首先使用一个步长为2的带有通道混洗分组卷积的残差下采样模块对特征图进行下采样，然后使用三个步长为1的带有通道混洗分组卷积的残差模块对特征图进行学习。
Stage3：核心构建模块，首先使用一个步长为2的带有通道混洗分组卷积的残差下采样模块对特征图进行下采样，然后使用七个步长为1的带有通道混洗分组卷积的残差模块对特征图进行学习。
Stage4：核心构建模块，首先使用一个步长为2的带有通道混洗分组卷积的残差下采样模块对特征图进行下采样，然后使用三个步长为1的带有通道混洗分组卷积的残差模块对特征图进行学习。
Conv5：标准1×1卷积，用于整合和提升特征维度。
GlobalPool： 7×7的全局平均池化，将最后一个Stage输出的7x7的特征图直接降维成1×1。
FC：全连接层，将GlobalPool后的向量映射到1000个类别上。
FLOPs：浮点运算次数，一次计算​​总共需要多少次浮点运算。
of Weights：模型参数量。

通过一个​​复杂度系数​​Output channels来​​调控​​整个网络中​​大多数层​​的通道数，从而得到不同计算量和精度水平的模型，以适应不同的硬件需求。

---

四、EfficientNet

1、EfficientNet V1

EfficientNet V1论文地址

1.网络宽度、深度与分辨率

a）baseline基线模型
假设是一个设计成熟的初始模型，它的​​宽度​​、​​深度和​​分辨率​​都有固定的初始值。往后的所有改动都是基于该模型结构进行的。
resolution H×W：固定的输入分辨率。
layer_i：固定的模型层数。
#channels：固定的通道数。

b）width scaling宽度缩放​
修改基线模型，增加模型每一层的通道数，深度和分辨率不作修改。
width：增加后的通道数。

增加网络的通道数能够学习到更多信息的特征，对于较浅的网络模型也更容易训练。
但通道数过大且深度较浅的网络很难学习到更深层次的特征，精度的提升有限，容易饱和。

c）depth scaling深度缩放
修改基线模型，加深模型的网络层数，宽度和分辨率不作修改。
deeper：加深后的网络层数。

增加网络的深度能够得到更加丰富、复杂的特征。
但网络层数过深会面临梯度消失，训练困难的问题。

d）resolution scaling分辨率缩放​
修改基线模型，扩大模型的输入图像的分辨率，宽度和深度不作修改。
higher resolution：扩大后的输入分辨率。

增加输入网络的输入分辨率能够获得更高细粒度的特征信息。
但过高的输入分辨率，计算量会呈平方级增长，参数量也会增多。

d）compound scaling复合缩放
修改基线模型，增加模型每一层的通道数，加深模型的网络层数，扩大模型的输入图像的分辨率。

​​深度、宽度和分辨率这三个维度是相互依赖的​​，更高的分辨率需要更深的网络来增加感受野，也需要更宽的网络来捕捉更细粒度的特征。单独缩放任何一个维度，模型性能都会很快达到瓶颈。

2.具体的复合模型缩放方法

$$\underset{d,w,r}{\max }Accuracy(N(d,w,r))$$
$$N(d,w,r)=\underset{i=\mathrm{1...}s}{⨀}{\hat{F}}_i^{d\cdot {\hat{L}}_i}(X_{(r\cdot {\hat{H}}_i,r\cdot {\hat{W}}_i,w\cdot {\hat{C}}_i)})$$
$$Memory(N)\le target\_memory$$
$$FLOPs(N)\le target\_flops$$

$N$：表示神经网络N。
$d,w,r$：表示深度系数d、宽度系数w、分辨率系数r三个复合缩放参数。
${⨀}_{i=\mathrm{1...}s}$：表示连续堆叠，i代表网络的​​阶段模块。
${\hat{F}}_i$：表示第i个阶段的​​基础模块或​​卷积层。
${\hat{L}}_i$：表示第 i个阶段​​重复${\hat{F}}_i$块的次数。
$X$：表示输入到第i个阶段的​​特征矩阵​​。
${\hat{H}}_i,{\hat{W}}_i,{\hat{C}}_i$：表示第 i个阶段的​​特征图高度H、宽度​W和通道数​​C。
max Accuracy：表示​​训练并评估​​网络N后得到的最优精度。
FLOPs(N)：表示​网络N完成一次前向传播所需的​​浮点运算次数​​。
​​Memory(N)​​：表示网络N运行时所需要占用的​​内存​​。
target_memory：表示预先设定的memory限制。
target_flops：表示预先设定的FLOPs限制。

对于输入到第i个阶段的​​特征矩阵X，使用分辨率系数r对特征矩阵的宽高进行缩放，使用宽度系数w对特征矩阵的通道数进行缩放。缩放后的特征矩阵X在基础模型${\hat{F}}_i$中​​重复学习受深度系数缩放影响的$d\cdot {\hat{L}}_i$次，最后按照不同阶段顺序进行堆叠，最终构成了完整的神经网络$N(d,w,r)$。

该公式的目的是寻找最优的缩放参数(d, w, r)，使得由这些参数缩放后生成的神经网络 N的​​准确率（Accuracy）最高。但是要求要满足约束条件，就是​缩放后的网络N其​​计算复杂度（FLOPs）​​ 和​​内存占用（Memory）必须分别小于预先设定的目标值target_flops和target_memory。并不是随意地增加网络的深度、宽度或分辨率，而是通过这个数学公式，​​系统性地​​且​​在计算资源与内存的严格约束下​​，搜索出同时缩放这三个维度的最佳比例，从而得到最高精度的模型。

以MobileNet V3为基线模型，使用的是MBConv模块，使用深度、宽度、分辨率和复合方案对模型进行不同的修改，对训练出来的不同模型进行比对，对比结果如上图所示。

3.层结构与模型结构

input​​：表示输入特征图。
​​1×1 Conv​​：表示1×1标准卷积，作用是​​通道数升维。
​​SiLU：表示Swish激活函数，曲线连续且光滑，x>0时具有线性，x<0时具有非线性。
​​3×3 DWConv：表示​​3×3深度可分离卷积，作用是提取特征图的空间特征。
GAP​​：表示全局平均池化Global Average Pooling，作用是把空间信息压缩为一维特征向量。
​​FC1：表示全连接层，作用是降维和捕获通道间的关系。
​​FC2：表示全连接层，作用是恢复原始的通道维度。
​​Sigmoid：表示Sigmoid激活函数，作用是将输出权重归一化到[0, 1]之间，计算每个通道的权重参数。
$⨂$：表示Scale操作，作用是将得到的权重逐通道乘回深度卷积后的特征图上，突出重要通道抑制不重要通道。
1×1 Conv​​：表示1×1标准卷积，作用是​​通道数降维。
​​Stochastic Depth​​：表示深度方向正则化技术，作用是随机简化网络深度，增强泛化能力
$⨁$：表示Shortcut(Add)操作，作用是将输入特征​​直接​​与核心路径输出相加，实现残差跳跃连接，要求输入与输出维度相同。
output​​​​：表示输出特征图。

Dropout机制是在且只在训练中以一定概率将某个神经元输出置零，目的​是防止全连接层过拟合，促进神经元独立学习。
​​Stochastic Depth机制也叫DropConnect机制，在且只在训练中以一定概率直接丢弃整个MBConv块，仅保留捷径分支。目的是随机简化网络深度，模拟集成学习效果，增强泛化能力，并在一定程度上缓解梯度消失问题，帮助训练更深的网络。

这是一个带SE模块的MBConv模块，其中MBConv模块就是倒残差移动瓶颈块，而GAP​​→ FC1→SiLU→ FC2→Sigmoid​​→$⨂$操作构成的就是​​SENet注意力模块​​。

Stage：表示网络的不同阶段。
Operator：表示该阶段所使用的网络模块或算子。
Resolution：表示该阶段输入特征图的分辨率
Channels：表示该阶段输出特征图的通道数。
Layers：表示该阶段Operator块重复堆叠的次数，也就是模型的网络层数。
MBConvX：表示倒残差移动瓶颈块，其中X表示扩展因子，通过1×1标准卷积将输入通道数扩展为原来的X倍。k表示DWConv使用的卷积核大小，主要使用3×3和5×5大小的卷积核。
Conv1×1 & Pooling & FC​：表示网络的​​头部Head，使用1×1卷积对通道数进行升维以整合所有特征，接着进行全局池化Pooling将每个通道的二维特征图压缩成一个标量，最后通过全连接层FC输出分类结果。
Stride：表示步长，在模块的第一个3×3 Conv或DWConv中会使用Stride=2操作进行下采样，这与Resolution相互对应，分别位于Stage1、Stage3、Stage4、Stage5、Stage7阶段。

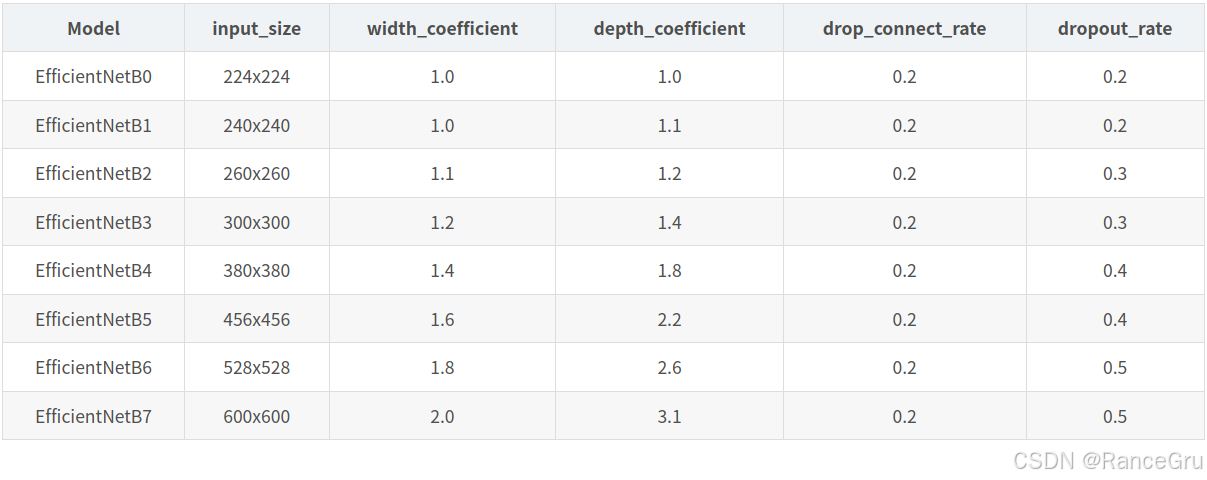
以上模型网络名为EfficientNet-B0模型，是整个EfficientNet系列的​​基础网络，通过复合缩放方法对模型进行调整，从而衍生出性能更强的EfficientNet-B1到B7模型。
图片来源

EfficientNet V1网络模型的性能参数对比图：

2、EfficientNet lite

EfficientNet-lite网络模型脱胎于EfficientNet V1网络模型，是 Google 专门为手机、IoT等边缘设备和 CPU平台推理优化的“硬件友好”版本。

1.激活函数

在EfficientNet-lite网络模型中，使用Relu6激活函数替代SiLU激活函数，SiLU激活函数激活复杂度高，并且对量化有不利影响。将其全部替换为ReLU6激活函数​​。

对于ReLU6激活函数而言，当输入值小于0的时候，默认都将它置0。在[0,6]区间内，不会改变它的输入值，但是当输入值大于6的时候，就会将输出值置为6。

ReLU6激活函数是移动端推理的“黄金标准”，计算简单，所有硬件都对其有极致优化，并且其截断特性（min(max(0, x), 6)）在量化时能保持数值稳定性。

2.​​注意力机制​​

在EfficientNet-lite网络模型中，去除SE模块，简化结构，减少内存访问。

对于SE模块而言，需要在整个特征图上进行全局平均池化和大量广播操作，将向量扩展到整个空间尺寸，大量细碎的操作也会增加内存访问开销，对 CPU 缓存不友好。

移除SE模块虽然损失了一点精度，但换来巨大的速度提升，使EfficientNet-lite网络模型更适合在边缘设备上高效运行。

EfficientNet-lite相对于EfficientNet V1虽然牺牲了少量理论精度，却换来了在边缘设备上巨大的速度和易用性的提升​​。

3、EfficientNet V2

EfficientNet V2论文地址

1.EfficientNet V1训练瓶颈

使用大分辨率图像进行训练会很慢：
总所周知，大尺度图像需要消耗更多的内存成本，而训练平台GPU和TPU的总内存是固定的，同样的内存总量能支持的小尺度图像数量比大尺度图像的数量更多。所以图像的尺寸越小，模型的FLOPs和内存访问成本越小，batch批量越大，能提高的训练速度越多。

在以下图表中，512×512输入和380×380输入的模型准确率相近，但是512×512输入在GPU和TPU中在小batch中还能运行，但是在大batch中会报爆显存OOM。而380×380输入在GPU和TPU中在小batch中也能运行，且每秒能处理的batch个数会比512×512输入更多，在大batch中不会爆显存OOM。

深度卷积在模型后期阶段计算高效，但在模型早期阶段计算缓慢：
虽然DW Conv相比标准卷积拥有更少的参数以及更小的FLOPs，但算子未必能有很好的支持，在模型早期，通道数较少，使用标准卷积进行计算会更快。在模型后期，通道数较多，使用DW Conv进行计算会更快。

No fused不使用标准卷积，相对其他方案而言，参数量和浮点运算次数最少，但是在GPU和TPU中每秒能处理的batch个数是最少的。
Fused stage 1-3中使用标准卷积，相对No fused而言，参数量和浮点运算次数会少量增加，在GPU和TPU中每秒能处理的batch个数明显增多。
Fused stage 1-5中使用标准卷积，相对Fused stage 1-3而言，参数量和浮点运算次数会明显增加，在GPU和TPU中每秒能处理的batch个数少量增多。
Fused stage 1-7中使用标准卷积，相对Fused stage 1-5而言，参数量和浮点运算次数会大量增加，在GPU和TPU中每秒能处理的batch个数反而下降。

不过现代GPU对DW Conv算子提供了专门的硬件加速支持，所以这个问题会有所改善，不需要很担忧。只不过计算密度相对较低，可能会受内存带宽制约，频繁的内存访问可能导致实际FLOPS效率低于理论值。

平均放大每个阶段是次优的：
在EfficientNet V1中，使用简单的复合缩放策略对每个stage的深度和宽度都进行了同等放大。但每个stage对网络的训练速度以及参数数量的贡献并不相同，所以直接使用同等缩放的策略并不合理，应该使用非均匀复合缩放策略。

2.层结构与模型结构

MBConv 结构：
第一层（Conv1×1）：1×1 标准卷积，通道数升维，从C→4C。
​​第二层（depthwise conv3×3）：3×3 DW卷积，进行特征提取，通道数保持不变​。
第三层（SE）：SE 注意力模块，突出重要通道，抑制不重要通道。
​​第四层（Conv1×1）：1×1 标准卷积，通道数降维，从4C→C。
​​跳跃连接$⨁$：输入特征​​直接​​与核心路径输出相加，要求输入与输出维度相同。

Fused-MBConv 结构：
第一层（Conv3×3）：3×3标准卷积，通道数升维，从C→4C，同时进行特征提取。
​​第二层（SE）：SE 注意力模块，突出重要通道，抑制不重要通道。
​​第三层（Conv1×1）：1×1 PW卷积，通道数降维，从4C→C。
​​跳跃连接$⨁$：输入特征​​直接​​与核心路径输出相加，要求输入与输出维度相同。

在MBConvde的倒残差结构中，深度可分离卷积由DWConv和PWConv操作组成，虽然FLOPs计算量很低，但在GPU等具有高并行计算能力的硬件上，其内存访问效率并不高。
一个融合的、更大的标准卷积操作往往能更充分地利用GPU的并行计算能力，从而​​实际运行速度更快​​。

在网络模型结构的浅层，特征图尺寸较大，通道数较少，使用此阶段MBConv需要计算三次卷积，而Fused-MBConv需要只需要计算两次卷积。
在网络的​​浅层使用Fused-MBConv​​，在​​深层继续使用高效的MBConv​​，实现了速度和精度的完美平衡。

Stage：表示网络的不同阶段。
Operator：表示该阶段所使用的网络模块或算子。
Stride：表示步长，在模块的第一个3×3 Conv或DWConv中会使用Stride=2操作进行下采样。
Channels：表示该阶段输出特征图的通道数，实际的模型实现的时候通道数又进行了调整，与表格不完全一致。
Layers：表示该阶段Operator块重复堆叠的次数，也就是模型的网络层数。
Fused-MBConvX：表示倒残差移动瓶颈块，其中X表示扩展因子，通过3×3标准卷积对通道数升维的同时进行特征提取，通过SE 注意力模块计算通道权重，通过1×1标准卷积对通道数降维。
MBConvX：表示倒残差移动瓶颈块，其中X表示扩展因子，通过1×1标准卷积对通道数升维，通过3×3DWConv进行特征提取，通过SE注意力模块计算通道权重，通过1×1标准卷积对通道数降维。
SE0.25：SE通道注意力机制主要由GAP​​→ FC1→SiLU→ FC2→Sigmoid​​→$⨂$等操作组成，为了降低模型的复杂度和参数量，​​第一个全连接层FC1会进行降维，所以第一个全连接层的输出神经元个数 = 输入通道数 C × 0.25​​​，不过在实现的时候Fused-MBConv和MBConv模块没有使用SE模块，以减少模型的内存访问开销。
Conv1×1 & Pooling & FC​：表示网络的​​头部Head，使用1×1卷积对通道数进行升维以整合所有特征，接着进行全局池化Pooling将每个通道的二维特征图压缩成一个标量，最后通过全连接层FC输出分类结果。
​​

Stage 0: 初始阶段，对原始输入图像进行第一次下采样和通道升维​，同时进行快速特征提取。
Stage 1 ~ 3: 早期阶段，连续使用Fused-MBConv加速构建特征图，保持精度的同时提升计算速度。
Stage 4 ~ 6: 中后期阶段，连续使用MBConv更快更好地提取和融合复杂特征，保证模型的精度和容量。

EfficientNet V2网络模型的性能参数对比图：

---

五、GhostNet

1、GhostNet V1

GhostNet V1论文地址

在深度卷积神经网络中，中间层的输出特征图通常会包含丰富甚至冗余的特征图，其中一些特征图可以通过对另一些特征图基于某种简单的操作变换获取，比如仿射变换和小波变换这些低成本的线性运算。
截取一份经过卷积处理的特征图组，其中一些特征图具有一定的相似性。 可以通过廉价操作将一个特征图变换为另一个相似的特征图，可以认为变换后的特征图是变换前特征图的一种幻像。

1.Ghost模块​​工作原理

(a)标准卷积层
$$Y=X\ast f+b$$

$X$表示输入特征图，$X\in {\mathbb{R}}^{h\times w\times c}$，$h$表示输入特征图的高度，$w$表示输入特征图的宽度，$c$表示输入特征图的通道数。
$f$表示卷积核，$f\in {\mathbb{R}}^{k\times k\times c\times n}$，$k\times k$表示卷积核的尺度，$c$表示输入特征图的通道数，$n$表示输出特征图的通道数。
$Y$表示输出特征图，$Y\in {\mathbb{R}}^{h^{\prime }\times w^{\prime }\times n}$，$h^{\prime }$表示输出特征图的高度，$w^{\prime }$表示输出特征图的宽度，$n$表示输出特征图的通道数。
$b$表示可选的偏置项，$\ast$表示卷积操作。

$$F_{std}=D_K\cdot D_K\cdot M\cdot N\cdot D_F\cdot D_F=k\cdot k\cdot c\cdot n\cdot h^{\prime }\cdot w^{\prime }$$

(b)Ghost模块

​​第一步：生成内在特征图Intrinsic Feature Maps

$$Y^{\prime }=X\ast f^{\prime }$$

$X$表示输入特征图，$X\in {\mathbb{R}}^{h\times w\times c}$，$h$表示输入特征图的高度，$w$表示输入特征图的宽度，$c$表示输入特征图的通道数。
$f^{\prime }$表示更少数量​​的卷积核，$f^{\prime }\in {\mathbb{R}}^{k\times k\times c\times m}$，$k\times k$表示卷积核的尺度，$c$表示输入特征图的通道数，$m$表示​​更少数量​​的输出特征图通道数，其中$m=\frac{C_{out}}{s}$，s是一个压缩系数。
$Y^{\prime }$表示内在特征图，$Y^{\prime }\in {\mathbb{R}}^{h^{\prime }\times w^{\prime }\times m}$，$h^{\prime }$表示输出特征图的高度，$w^{\prime }$表示输出特征图的宽度，$m$表示​​更少数量​​的输出特征图通道数，其中$m=\frac{C_{out}}{s}$，s是一个压缩超参数。
$\ast$表示1×1标准卷积操作。

第二步：生成幻影特征图Ghost Feature Maps

$$y_{ij}={\Phi }_{i,j}(y_i^{\prime }),\forall i=1,...,m;j=1,...,s;$$

$y_i^{\prime }$表示内在特征图$Y^{\prime }$的第$i$个通道的特征图，$i=1,...,m$。
${\Phi }_{i,j}$表示​​一个廉价线性变换操作，通常指DWConv，对于​​每一张​​内在特征图$y_i^{\prime }$，都会应用s次不同的$\Phi$操作，$j=1,...,s$，从而生成s张新的特征图。
$y_{ij}$表示由第i个内在特征图经过第j个变换后得到的Ghost特征图。

$$F_{Ghost}=k\cdot k\cdot c\cdot m\cdot h^{\prime }\cdot w^{\prime }+m\cdot (s-1)\cdot y_{ij}$$

第三步：特征图拼接
对于第一步生成的$m$个内在特征图Intrinsic Feature Maps，使用快捷分支Identity恒等映射到输出特征图中，然后将第二步生成的$m\cdot (s-1)$个 Ghost 特征图按照顺序在通道维度上进行拼接，共同构成最终的$n=m+m\cdot (s-1)=m\cdot s$个输出特征图。

2.层结构与模型结构

左边模块结构：
第一层Ghost module+BN+ReLU：对输入特征进行通道升维和特征提取，然后进行归一化和激活处理。
​​第二层Ghost module+BN：对输入特征进行通道降维和特征提取，然后进行归一化处理。
第三层​​Add：Stride步长为1，使用跳跃连接将​​第二层的输出与第一层的​​输入​​直接进行​​元素级相加。

右边模块结构：
第一层Ghost module+BN+ReLU：对输入特征进行通道升维和特征提取，然后进行归一化和激活处理。
​​第二层DWConv+BN：Stride​​步长为2，对输入特征进行下采样​​，将尺寸减半通道降维以及特征提取，然后进行归一化处理。
​​第三层Ghost module+BN：对输入特征进行通道降维和特征提取，然后进行归一化处理。
第四层DWConv+PWConv：由于第二层的下采样操作，导致不能直接进行跳跃连接，所以在实际实现中旁路会先使用DWConv对输入特征进行下采样​​，将尺寸减半通道降维。再使用1×1标准卷积调整通道数，使得输入和输出特征图的形状一致。上图并没有把旁路的操作绘制出来。
第五层​​Add：Stride步长为2，使用跳跃连接将​​第三层的输出与第四层的​​输入​​直接进行​​元素级相加。

​​Input：表示输入特征图的尺寸
Operator：表示该阶段所使用的网络模块或算子。
exp：表示ghost模块第一层的升维通道数。
out：表示ghost模块降维后的输出通道数。
SE：表示是否使用SE注意力机制，1代表使用，-代表未使用。
Stride：表示步长，在模块的第一个3×3 Conv或DWConv中会使用Stride=2操作进行下采样。
G-bneck：表示ghost模块。

​​在整个模型早期，使用带步长的卷积和少量的模块堆叠对特征图快速降维​​，减少计算量。在模型中后期时候，对于小尺寸特征图使用更多的模块堆叠加强特征学习。

一方面使用廉价线性变换操作替代大量冗余的标准卷积，在保证表现力的前提下极致地压缩了计算量FLOPs和参数量，另一方面使用倒残差结构的先升维再降维操作提高梯度流动和特征表达，最后还对控制每一层模型的通道数数量，减少宽度方向的计算量。

模型在部分关键层使用SE模块，以极小的计算代价换取显著的性能提升，目的是为了避免因为对模型计算量的过度压缩而导致的精度大幅下滑。​​

2、GhostNet V2

GhostNet V2论文地址

1.解耦全连接注意力机制DFC Attention

卷积网络模型中常见的注意力机制有SE（Squeeze-and-Excitation）、CBAM（Convolutional Block Attention Module）和CA（Coordinate Attention），而DFC（Decoupled Fully Connected）注意力机制是在前三者的基础之上提出的。

Input feature：表示C×H×W大小的输入特征图。
Down-sample：表示下采样操作，通常是使用池化下采样或卷积下采样来实现。
Vertical FC：表示垂直全连接层，对​​每列数据进行全连接操作，处理同一列内不同行的信息，捕获特征在​​垂直方向​​上的长期依赖关系。
Horizontal FC：表示水平全连接层，对​​每行数据进行全连接操作，处理同一行内不同列的信息，捕获特征在​​水平方向​​上的长期依赖关系。
Up-sample：表示上采样操作，通常使用插值上采样或转置卷积上采样来实现。
Attention map：表示C×H×W大小的输出注意力特征图。

DFC注意力机制通过下采样降低计算量，再通过垂直和水平方向对全连接层进行解耦，高效地建模空间上的远距离依赖关系，最终生成一张注意力图对特征图实现增强重要特征，抑制无用特征。​

$$a_{hw}=\sum _{h^{\prime },w^{\prime }}{F}_{hw,h^{\prime }{w}^{\prime }}⨀z_{h^{\prime }{w}^{\prime }}$$
$$a_{hw}^{\prime }=\sum _{h^{\prime }=1}^H{F}_{h,h^{\prime }w}^H⨀z_{h^{\prime }w},h=1,2,...,H;w=1,2,...,W;$$
$$a_{hw}=\sum _{w^{\prime }=1}^W{F}_{w,h{w}^{\prime }}^W⨀a_{h{w}^{\prime }}^{\prime },h=1,2,...,H;w=1,2,...,W;$$

$a_{h,w}$：表示一个长度为C一维向量，由输出特征图中所有通道的特征矩阵中的$(h,w)$位置上的特征点组成的。
$h,w,h^{\prime },w^{\prime }$：表示输入和输出特征图的高与宽，也表示在某个位置上的坐标
$F{}_{hw,h^{\prime }{w}^{\prime }}$：表示二维注意力权重矩阵，每一项对应一个输出位置$(h,w)$与一个输入位置$(h^{\prime }{w}^{\prime })$的权重向量，每一个位置指向的是一个标量。
$F_{h,h^{\prime }w}^H$：表示垂直方向注意力权重矩阵
$F_{w,h{w}^{\prime }}^W$：表示水平方向注意力权重矩阵
$z_{h^{\prime },w^{\prime }}$：表示一个长度为C一维向量，由输入特征图中所有通道的特征矩阵中的$(h^{\prime },w^{\prime })$位置上的特征点组成的。
$z_{h^{\prime },w}$：表示一个长度为C一维向量，由一个固定列中所有通道的特征矩阵中的$(h^{\prime },w)$位置上的特征点组成的。
$a_{h,w^{\prime }}^{\prime }$：表示一个长度为C一维向量，由一个固定行中所有通道的特征矩阵中的$(h,w^{\prime })$位置上的特征点组成的。
$HW$：表示注意力权重矩阵​​的高与宽，表示在某个位置上的行或列
$⨀$：表示逐元素相乘。
$\sum$：表示对输入特征图的所有空间位置进行求和。

公式1是一个理想的全局注意力机制。
在公式一中，为了得到输出特征图$a_{h,w}$上的目标位置$(h,w)$上的值，需要让输入特征图上所有位置与权重$F{}_{hw,h^{\prime }{w}^{\prime }}$进行逐元素相乘，然后对每个位置的结果进行求和。

公式2和公式3是基于公式1分解而来的垂直+水平注意力机制。
在公式2中，为了得到垂直处理的输出特征图$a_{h,w}^{\prime }$上的目标位置$(h,w)$的值，需要让输入特征图上固定列的每行位置与权重$F_{h,h^{\prime }w}^H$进行逐元素相乘，然后对固定列上所有位置的结果进行求和。

在公式3中，为了得到水平处理的输出特征图$a_{h,w}$上的目标位置$(h,w)$的值，需要让输入的垂直处理特征图上固定行的每列位置与权重$F_{w,h{w}^{\prime }}^W$进行逐元素相乘，然后对固定行上所有位置的结果进行求和。

输入特征图有C个通道，那么在位置$(h^{\prime },w^{\prime })$上，会有C个值可以组成一个一维向量，这个一维向量在DFC注意力机制计算中会和同一个权重$F$相乘，然后与同通道不同位置的值相加，最后输出的也是一个长度为C的一维向量。

在以上图片中，从左到右开始，第一个是输入特征图$z_{h^{\prime },w^{\prime }}$，第二个是垂直处理的中间态特征图，第三个是垂直处理输出特征图$a_{h,w}^{\prime }$，第四个是水平处理的中间态特征图，第五个是水平处理输出特征图$a_{h,w}$

Vertical/Horizontal Attention：表示垂直和水平注意力，也就是DFC Attention，是公式二和三的体现，计算复杂度为O(N)。
Full Attention：表示全注意力，也就是传统二维注意力机制，是公式一的体现，计算复杂度为O(N²)。
Layer 5，10，15：表示不同深度的网络层。
热力刻度条：表示注意力权重的大小。

对比DFC Attention与Full Attention在不同网络深度下的表现：
在Layer 5时期，Full Attention对于特征图上的所有特征点都有丰富的注意力表达。而DFC Attention只有少部分特征点赋予注意力表达，大部分特征点没有变化。
在Layer 10时期，Full Attention对于特征图上的所有特征点都有丰富的注意力表达。而DFC Attention能够对大部分特征点赋予注意力表达，只有小部分特征点没有变化。
在Layer 15时期，Full Attention对于特征图上的所有特征点都有丰富的注意力表达。而DFC Attention能够对所有特征点赋予注意力表达。

所以DFC Attention随着网络深度的增加，注意力的表达能力会不断增强，逐渐追上Full Attention的性能。

2.层结构与模型结构

Input：表示输入特征图。
Ghost Branch：表示使用Ghost模块处理的分支。
Attention Branch：表示使用注意力模块处理的分支。
Multiply：表示将两个分支的输出进行​​逐元素相乘。
Output：表示输出特征图。
Focused patch：表示目标特征点。
Participated patches in Ghost branch：表示使用Ghost模块计算目标特征点时参与处理的特征点。
Participated patches in Attention branch：表示使用注意力模块计算目标特征点时参与处理的特征点。

在模型结构中，对于计算特征图上的某个特征点需要使用两个分支进行。
使用Ghost模块的分支会对目标特征点周围的特征点进行关联计算，这里常用的是3×3DWConv，输出的是一个特征图，感受野为3×3。
使用注意力模块的分支会对目标特征点所在的特征图的所有特征点进行关联计算，这里常用的是DFC Attention，输出的是一个[0,1]的注意力权重矩阵，感受野为H×W。
将两个分支的输出进行​​逐元素相乘，使用注意力权重对目标特征点进行动态校准，增强重要特征，抑制无用特征。

右边模块结构：
第一层Down-sample​​：对输入特征进行下采样，以降低计算成本。
​​第二层1×1 Convolution + BN：对输入特征进行卷积操作，实现通道变换和特征提取，然后进行归一化处理。
第三层Horizontal FC + BN：在​​水平方向​​上对每一行数据做一次高度为1宽度为W的全连接操作，以捕获全局水平信息，然后进行归一化处理。
第四层Vertical FC：在​​垂直方向​​上对每一列数据做一次高度为H宽度为1的全连接操作，以捕获全局垂直信息。
​​第五层Sigmoid：通过Sigmoid函数，将输出值归一化到[0, 1]范围，形成最终的注意力图。

左边模块结构：
第一层Ghost module+BN+ReLU：对输入特征进行通道升维和特征提取，然后进行归一化和激活处理。
​​第二层DFC Attention：根据输入特征​​计算一个注意力图，注意力图的大小与第一层的Ghost Module的输出相同。
​​第三层Mul：将​​第二个Ghost Module的输出​​与​​DFC Attention模块输出的注意力图​​进行​​逐元素相乘，对输入特征进行​​加权，增强重要特征，抑制无用特征。
​​第四层Ghost module+BN：对输入特征进行通道降维和特征提取，然后进行归一化处理。
第五层​​Add：Stride步长为1，使用跳跃连接将​​第二层的输出与第一层的​​输入​​直接进行​​元素级相加。

中间模块结构：
第一层Ghost module+BN+ReLU：对输入特征进行通道升维和特征提取，然后进行归一化和激活处理。
​​第二层DFC Attention：根据输入特征​​计算一个注意力图，注意力图的大小与第一层的Ghost Module的输出相同。
​​第三层Mul：将​​第二个Ghost Module的输出​​与​​DFC Attention模块输出的注意力图​​进行​​逐元素相乘，对输入特征进行​​加权，增强重要特征，抑制无用特征。
​​第四层DWConv+BN：Stride​​步长为2，对输入特征进行下采样​​，将尺寸减半通道降维以及特征提取，然后进行归一化处理。
​​第五层Ghost module+BN：对输入特征进行通道降维和特征提取，然后进行归一化处理。
第六层DWConv+PWConv：由于第二层的下采样操作，导致不能直接进行跳跃连接，所以在实际实现中旁路会先使用DWConv对输入特征进行下采样​​，将尺寸减半通道降维。再使用1×1标准卷积调整通道数，使得输入和输出特征图的形状一致。上图并没有把旁路的操作绘制出来。
第七层​​Add：Stride步长为2，使用跳跃连接将​​第五层的输出与第六层的​​输入​​直接进行​​元素级相加。

一方面通过廉价的DWConv操作和线性操作来“幻化”出更多的特征图，从而用更少的参数和计算量生成与普通卷积层相同数量的特征图。
另一方面通过轻量级的 ​​DFC Attention​​ 模块，为Ghost模块生成的特征图提供丰富的​​空间注意力权重​​，从而显著增强模型的表征能力。

3、GhostNet V3

GhostNet V3论文地址

1.层结构与模型结构

Training of 3×3 DWConv：表示在训练阶段使用的深度卷积重参数化结构，对输入特征图同时使用一个1×1DWConv、一个Identity快捷分支和n个3×3DWConv进行计算，最后对所有输出的特征图进行相加操作。
Training of 1×1 Conv：表示在训练阶段使用的标准卷积重参数化结构，对输入特征图同时使用n个1×1DWConv和一个Identity快捷分支进行计算，最后对所有输出的特征图进行相加操作。
DFC Attention：表示一个注意力机制，先使用下采样降低计算量，再通过垂直和水平方向对全连接层进行解耦，高效地建模空间上的远距离依赖关系，最终生成一张注意力图。
Ghost Module：表示一个Ghost模块，主要使用1×1 Conv生成内在特征图，3×3 DWConv生成幻影特征图，然后使用Concat沿通道方向拼接两个特征图。

Training of 3×3 DWConv和Training of 1×1 Conv主要在训练阶段替代Ghost模块中的3×3 DWConv操作和1×1 Conv操作。而在推理时会将这些多分支重参数化结构等价地“折叠”或“融合”成一个单一的3×3 DWConv操作和1×1 Conv操作，所以在推理时的使用的模型结构会和原来一样简洁高效，但性能却得到了提升。

此外在GhostNet V3中还提及使用知识蒸馏、学习率调度和数据增强等模型优化策略。

GhostNetV3网络模型在目标检测上的性能参数对比图：

---

六、其他

后续补充。。。

---

总结

这些高效卷积神经网络架构代表了轻量级CNN设计的演进历程，从单纯减少参数，到发明新卷积方式，再到考虑硬件特性、系统化缩放，最后到洞察特征冗余本身。它们的设计思想至今仍深刻影响着高效的模型设计。