当前位置：首页 > news >正文

【洛谷】算法竞赛中的树结构：形式、存储与遍历全解析

news 2025/9/20 6:25:01

文章目录

一、树在竞赛中的常见形式
二、树的存储
- 孩⼦表⽰法
- 实现⽅式⼀：⽤ vector 数组实现
- 实现⽅式⼆：链式前向星
- 深度优先遍历-DFS
- 宽度优先遍历-BFS
- DFS/BFS时空复杂度

一、树在竞赛中的常见形式

1、有序树和⽆序树
有序树：结点的⼦树按照从左往右的顺序排列，不能更改。
⽆序树：结点的⼦树之间没有顺序，随意更改。
一般遇到的都是无序树。

在这里插入图片描述

2、有根树和⽆根树
有根树：树的根节点已知，是固定的。
⽆根树：树的根节点未知，谁都可以是根结点。
一般遇到的都是⽆根树。

在这里插入图片描述

二、树的存储

树结构相对线性结构来说就⽐较复杂。存储时，既要保存值域，也要保存结点与结点之间的关系。实际中树有很多种存储⽅式：双亲表⽰法，孩⼦表⽰法、孩⼦双亲表⽰法以及孩⼦兄弟表⽰法等。
现阶段，我们只⽤掌握孩⼦表⽰法，学会⽤孩⼦表⽰法存储树，并且在此基础上遍历整棵树。后续会在并查集中学习双亲表⽰法。

孩⼦表⽰法

孩⼦表⽰法是将每个结点的孩⼦信息存储下来。
如果是在⽆根树中，⽗⼦关系不明确，我们会将与该结点相连的所有的点都存储下来。

在这里插入图片描述

接下来我们会讲解用两种方法实现孩子表示法。

实现⽅式⼀：⽤ vector 数组实现

在这里插入图片描述

上面示例输入里的每行 x, y 只表示 “x 和 y 之间有一条边”，但没明确谁是父节点、谁是子节点（比如 3 1 可以是 “3 是 1 的子节点”，也可以是 “1 是 3 的子节点”，但无向边本身不包含这个方向信息）。
虽然题目指定了 “1号是根节点”，但输入的边是无向的集合，本质上描述的是 “无根树的连接结构”。要得到 “以 1为根的有根树”，需要基于无根树的边结构，再从根节点 1 出发（通过 DFS/BFS 等遍历），才能推导并建立 “父 - 子” 的有向关系。

vector< int > edges[N];
表示创建N个元素的数组，每个元素的类型是vector< int，edges数组的每个元素表示树的一个结点，edges数组下标表示该结点存储的数值。

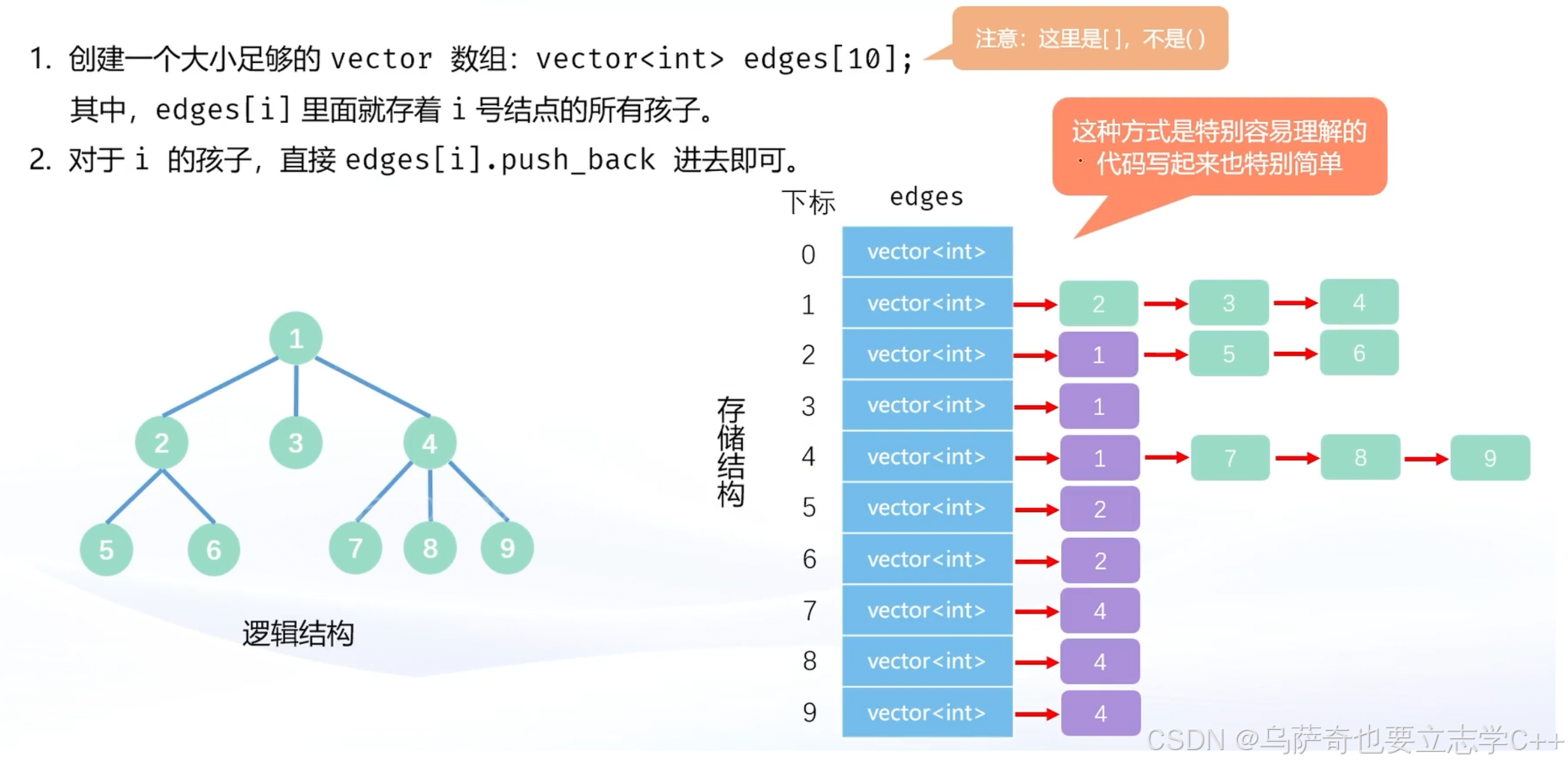
在这里插入图片描述

代码实现：
(注意第一组数据如 3 1 包含了两个结点信息，也就是说树一共有9个结点的话只需循环8次存储8个结点)

const int N = 1e5 + 10;  //表示数据最大值
int n;                   //表示其中一组数据的结点值
vector<int> edges[N]; //存储树int main()
{cin >> n; //n个结点for(int i = 1; i < n; i++){int a, b;cin >> a >> b;//a和b之间有一条边edges[a].push_back(b);edges[b].push_back(a);}return 0;
}

实现⽅式⼆：链式前向星

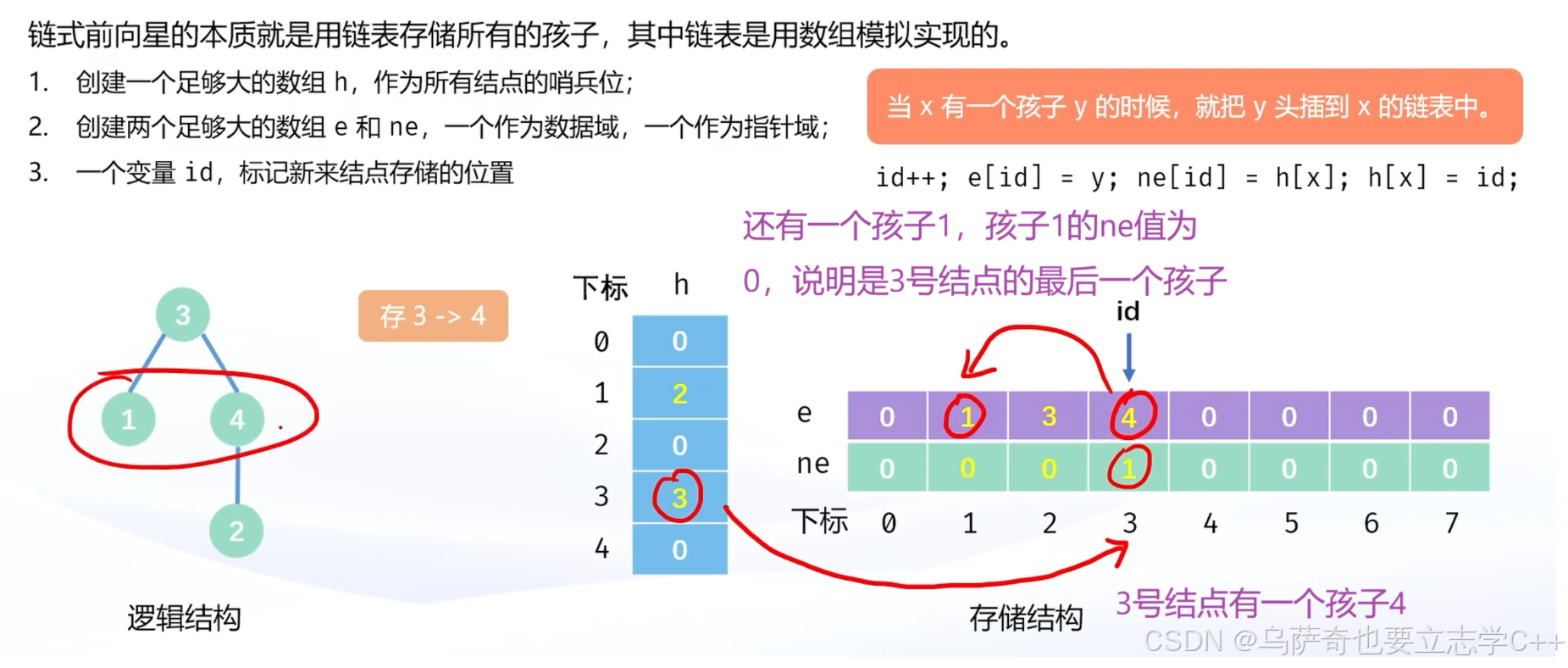
在这里插入图片描述

上面是把3-1 1-3 3-4 边用链式前向星存储的示意图
所以h[i]的值是i号结点的其中一个孩子位于链表物理结构数组的下标，也就是该结点对应链表第一个有效结点的值，可以基于它遍历与该结点所有相连的结点。

代码实现：
注意事项：代码实现中e和ne数组空间要开题目要求最大范围的两倍，因为存储结点时要把一条边存储两遍，对于用数组模拟链表来说存储一个结点就需要用两个数组元素空间来存储。

const int N = 1e5 + 10;  //表示数据最大值
int n;                   //表示其中一组数据的结点值
int h[N], e[2 * N], ne[2 * N], id;void add(int a, int b)
{//头插 把b头插到a的链表中++id;e[id] = b;ne[id] = h[a]; //插入结点指向链表第一个有效节点h[a] = id;     //该链表第一个有效结点变成插入的结点
}int main()
{cin >> n; //n个结点while (n--){int a, b;cin >> a >> b;//a和b之间有一条边add(a, b);//a,b不清楚父子关系，还需要把a头插到b的链表中add(b, a);}return 0;
}

深度优先遍历-DFS

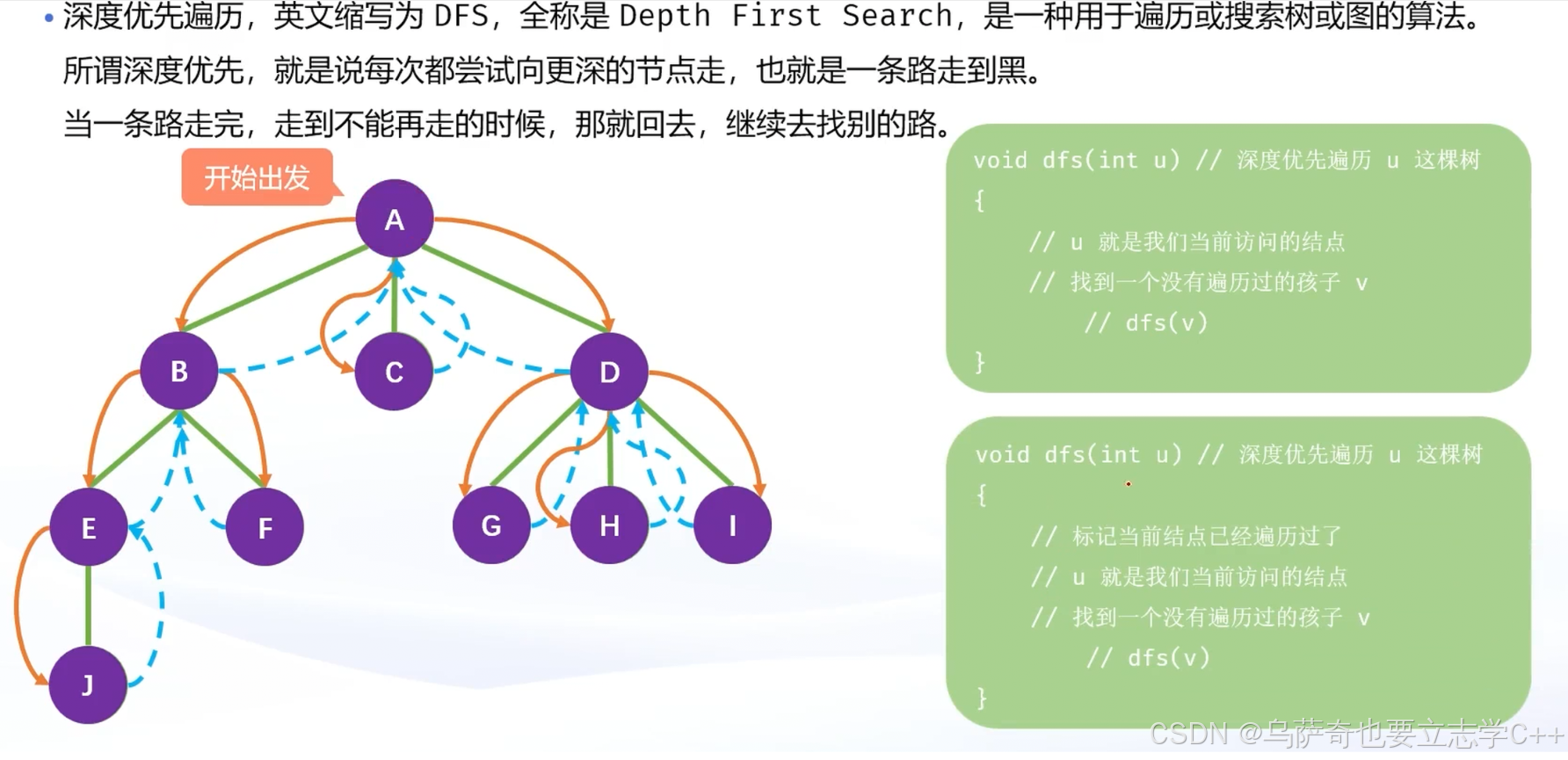
在这里插入图片描述

因为我们是按照无根树存储树结构的，孩子结点也存储了父节点的数据，所以递归函数是可能通过孩子结点又递归回去遍历父节点，这是不被允许的，所以我们需要用一个bool数组st标记已经被遍历过的结点，bool数组st下标和edges数组下标一一对应。

下面是用vector数组实现树的dfs遍历：

using namespace std;
#include <iostream>
#include <vector>const int N = 1e5 + 10;
vector<int> edges[N]; //存储树
bool st[N];           //标记被遍历过的结点void dfs(int u)
{cout << u << " ";//标记遍历过的结点st[u] = true; //遍历当前结点的所有孩子结点for (auto e : edges[u]){//当结点没被标记再继续递归遍历if (!st[e]) {dfs(e);}}
}int main()
{//创建树int n;cin >> n;for (int i = 1; i < n; i++){int x, y;cin >> x >> y;edges[x].push_back(y);edges[y].push_back(x);}//dfsdfs(1);return 0;
}

下面是用链式前向星实现树的dfs遍历：

const int N = 1e5 + 10;
int h[N], e[2 * N], ne[2 * N], id;
bool st[N];
int n;void add(int x, int y)
{//y插入x所在链表++id;e[id] = y;ne[id] = h[x];h[x] = id;
}void dfs(int u)
{cout << u << " ";st[u] = true;//h[u]是当前结点其中一个孩子结点的数组下标for (int cur = h[u]; cur; cur = ne[cur]){//通过数组下标cur获取到数组元素child//通过child值判断该孩子结点是否被遍历过int child = e[cur];if (!st[child]){dfs(child);}}
}int main()
{//创建树cin >> n;for (int i = 1; i < n; i++){int x, y;cin >> x >> y;add(x, y);add(y, x);}//dfsdfs(1);return 0;
}

因为我们是把数据头插进链表，所以遍历每个结点的孩子结点时与用数组存储树的遍历顺序相反，最后的打印结果也和用数组存储树的结果相反。

宽度优先遍历-BFS

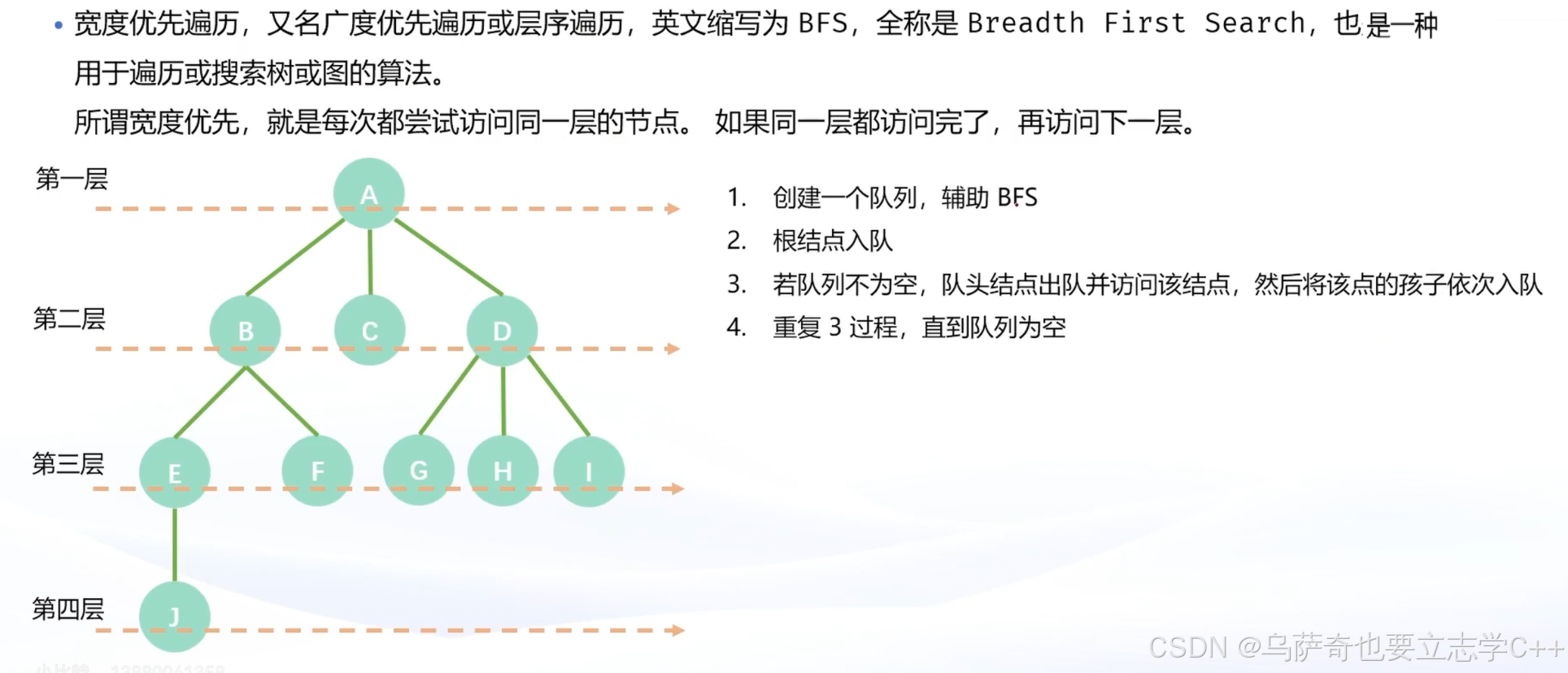
在这里插入图片描述

下面是用vector数组实现树的bfs遍历：

//用vector数组存树
const int N = 1e5 + 10;
vector<int> edges[N];   
bool st[N];
int n;void bfs(int u)
{queue<int> q;int x = 0;q.push(u);while (!q.empty()){x = q.front();q.pop();cout << x << " ";//打印后标记为truest[x] = true; for (auto e : edges[x]){if (!st[e]){//e没被标记过才插入队列q.push(e);}}}
}int main()
{//建树cin >> n;for (int i = 1; i < n; i++){int x, y;cin >> x >> y;edges[x].push_back(y);edges[y].push_back(x);}//遍历bfs(1);return 0;
}

下面是用链式前向星实现树的bfs遍历：

//用链式前向星存树
const int N = 1e5 + 10;
int h[N], e[2 * N], ne[2 * N], id;
bool st[N];
int n;void add(int x, int y)
{++id;e[id] = y;ne[id] = h[x];h[x] = id;
}void bfs(int u)
{queue<int> q;int x = 0;q.push(u);while (!q.empty()){x = q.front();q.pop();cout << x << " ";//打印后标记为truest[x] = true;//cur表示遍历到的数组下标int cur = h[x];for (cur; cur != 0; cur = ne[cur]){int child = e[cur];if (!st[child]){//child没被标记过才插入队列q.push(child);}}}
}int main()
{//建树cin >> n;for (int i = 1; i < n; i++){int x, y;cin >> x >> y;add(x, y);add(y, x);}//遍历bfs(1);return 0;
}