当前位置：首页 > news >正文

线性表---双链表概述及应用

news 2025/9/19 8:25:36

基本的概念认识

1. 核心概念：什么是双链表？

2. 双链表的基本结构

3. 双链表的优缺点

优点

缺点

基本运算操作

插入操作

删除操作

建立双链表

插入和删除实现函数

两个应用示例

双链表 vs. 单链表：如何选择？

总结

本文重点讲述线性表中的双链表存储结构及基本的实现过程，包含我自身的心得及思考，愿诸位能相比书上内容更好理解。

基本的概念认识

1. 核心概念：什么是双链表？

想象一下火车车厢：每节车厢（节点）都有两个连接器，一个连接前一节车厢，一个连接后一节车厢。车头（头节点）是起点，车尾（尾节点）是终点。你可以从车头走到车尾，也可以从车尾走回车头。这就是双链表。

官方定义：双链表（Doubly Linked List）是一种每个节点都包含两个指针的链表结构：一个指向其前驱节点 (prev)，一个指向其后继节点 (next)。这使得双向遍历成为可能。

一个典型的双链表节点在代码中这样定义：

typedef struct DNode//双链表
{ElemType data;struct DNode *prior;struct DNode *next;
}DLinkNode;

2. 双链表的基本结构

双链表有多种形式，最常见和实用的是 带头节点（哨兵节点）的双向循环链表。它的结构非常巧妙：

头节点 (哨兵节点)：不存储实际数据，prev指向尾节点，next指向第一个实际数据节点。它作为固定的起点和终点，极大地简化了插入和删除操作的边界判断。
循环：尾节点的 next指向头节点，头节点的 prev指向尾节点，形成一个环。

3. 双链表的优缺点

优点

双向遍历：可以从任意节点向前或向后遍历，提供了极大的灵活性。
高效的插入和删除：在已知某个节点位置时，插入或删除操作只需修改相邻节点的指针，时间复杂度为 O(1)。这比单链表（通常需要定位前驱节点，O(n)）和顺序表（需要移动元素，O(n)）更高效。
边界处理更简单：特别是带有哨兵节点的双链表，因为所有有效节点都有前驱和后继，使得头插和尾删等操作与中间操作一样简单。

缺点

内存开销更大：每个节点都需要额外的空间来存储前驱指针 (prev)。
实现略复杂：需要维护两个指针，插入和删除操作时指针的调整步骤稍多，容易出错（如产生循环引用或指针悬空）。

基本运算操作

插入操作

在双链表p所指后插入一个结点s，代码如下：

s->next=p->next;
p->next->prior=s;
s->prior=p;
p->next=s;

流程如图下：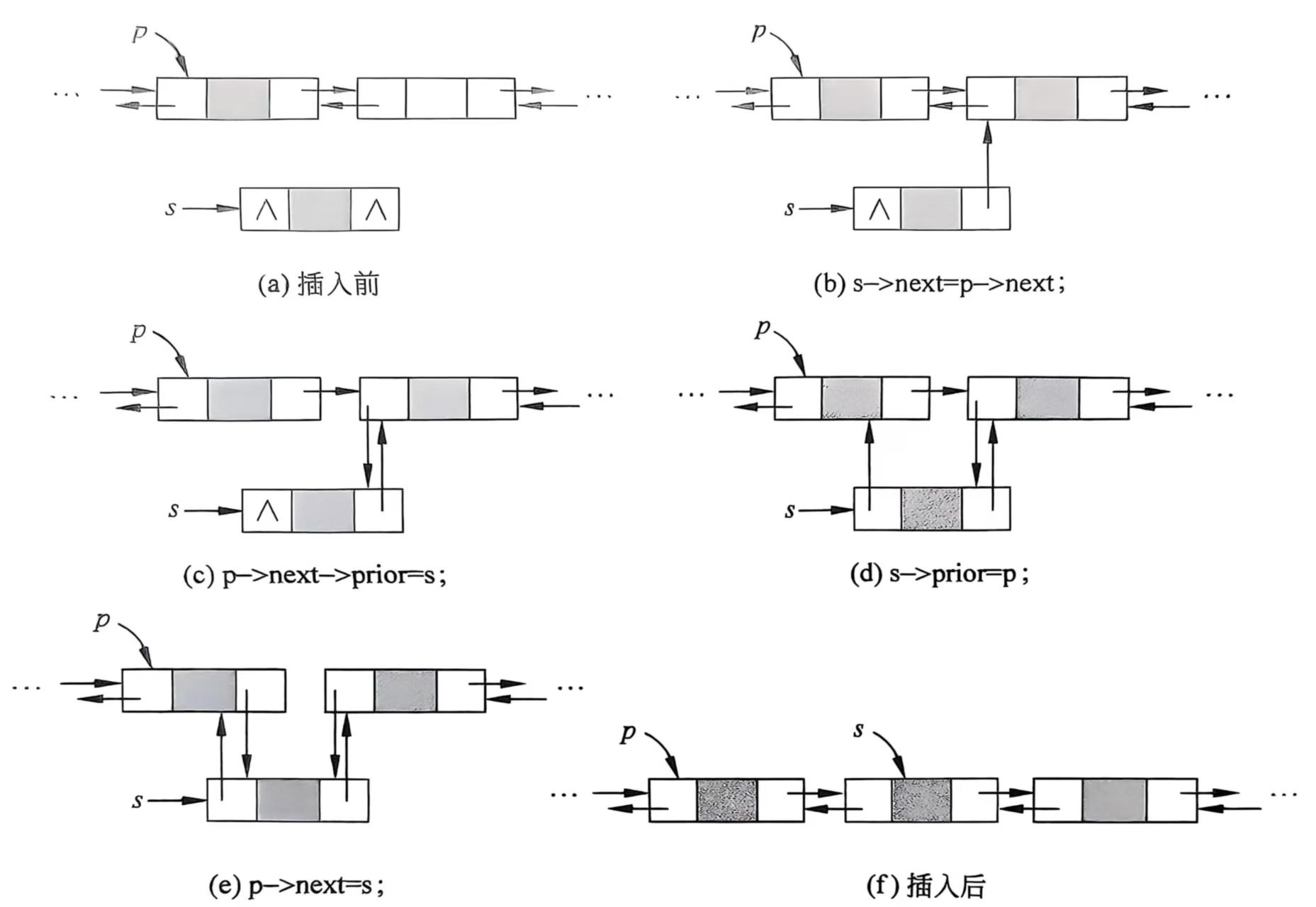

删除操作

删除p的后续结点，q是被删除的，代码如下：

p->next=q->next;
q->next->prior=p;

具体流程如下：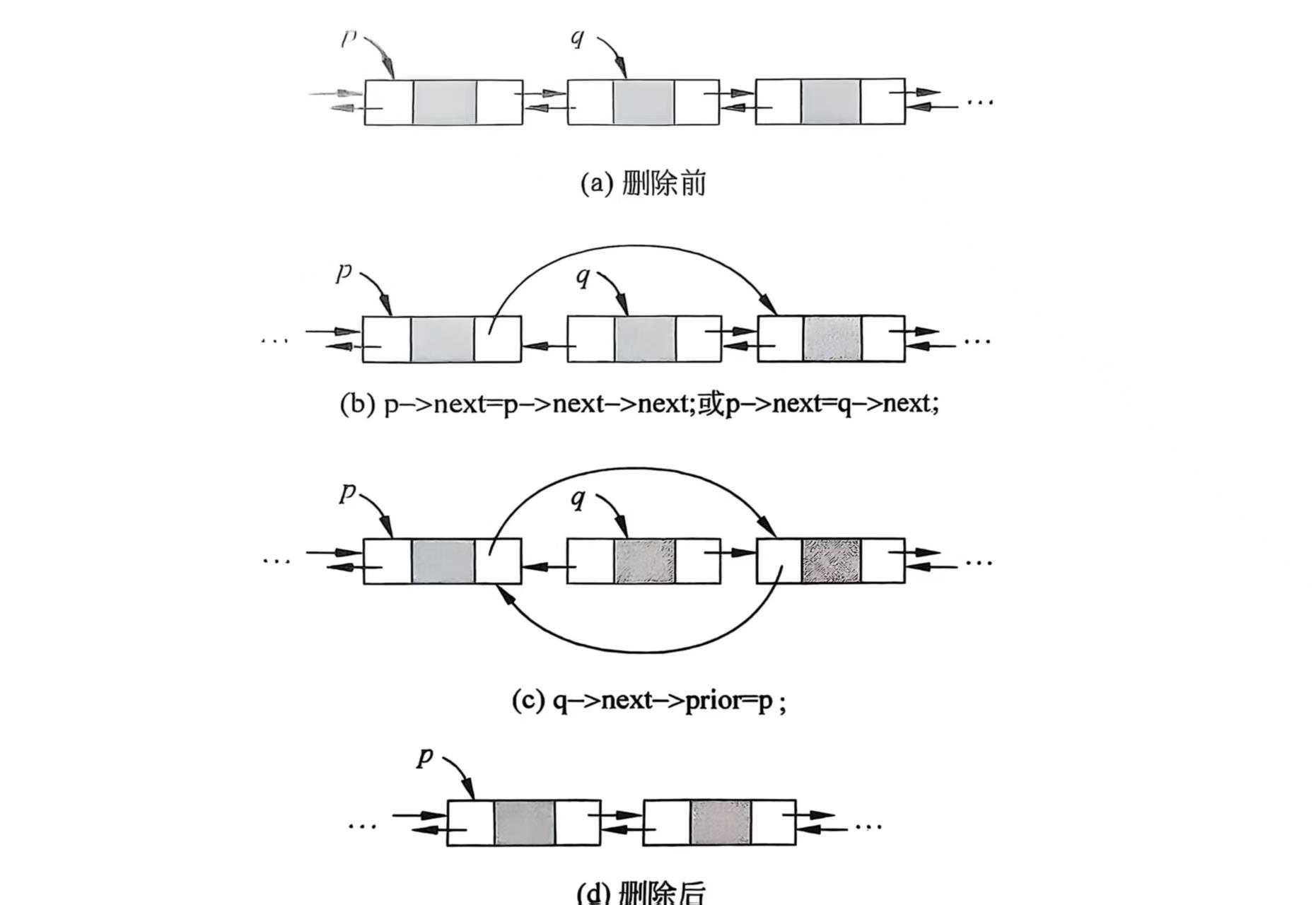

建立双链表

整体建立双链也有两种方法，头插法和尾插法，与我前一篇博客《单链表》类似。

头插法算法如下：

void CreateListF(DLinkNode *&L,ElemType a[],int n)
{DLinkNode *s;L=(DLinkNode *)malloc(sizeof(DLinkNode));L->next=NULL;for(int i=0;i<n;i++){s=(DLinkNode *)malloc(sizeof(DLinkNode));s->data=a[i];s->next=L->next;if(L->next!=NULL)L->next->prior=s;s->prior=L;L->next=s;}
}

作用：用头插法将数组 a中的 n个元素快速构建成一个双链表。新节点总是插入在头节点之后。
过程：
1. 创建头节点 L。
2. 循环 n次，每次创建一个新节点 s存储 a[i]。
3. 将 s插入到头节点 L和原第一个节点之间。
特点与结果：生成的链表中，元素的顺序与数组 a中的顺序相反。
通俗理解：像一叠盘子，你依次放入A、B、C，但每次都在最上面放。最后从上到下读就是C、B、A，顺序反了。

尾插法算法如下：

void CreateListR(DLinkNode *&L,ElemType a[],int n)
{DLinkNode *p,*r;L=(DLinkNode *)malloc(sizeof(DLinkNode));r=L;for(int i=0;i<n;i++){p=(DLinkNode *)malloc(sizeof(DLinkNode));p->data=a[i];r->next=p;p->prior=r;r=p;}r->next=NULL;
}

作用：用尾插法将数组 a中的 n个元素构建成一个双链表。新节点总是插入在链表尾部。
过程：
1. 创建头节点 L，指针 r始终指向当前链表的尾节点（初始时 r=L）。
2. 循环 n次，每次创建一个新节点 p存储 a[i]。
3. 将新节点 p链接到尾节点 r之后，然后更新 r指向新的尾节点 p。
特点与结果：生成的链表中，元素的顺序与数组 a中的顺序完全相同。
通俗理解：像排队，新来的人总是站在队伍最后面。队伍顺序就是大家来的顺序。

插入和删除实现函数

插入元素到第i个位置，算法如下：

bool ListInsert(DLinkNode *&L,int i,ElemType e)
{int j=0;DLinkNode *s,*p=L;if(i<=0)    return false;while(j<i-1&&p!=NULL){j++;p=p->next;}if(p==NULL)return false;else{s=(DLinkNode *)malloc(sizeof(DLinkNode));s->data=e;s->next=p->next;if(p->next!=NULL)p->next->prior=s;s->prior=p;p->next=s;return true;}
}

作用：在双链表的第 i个位置（位序，从1开始计数） 插入一个值为 e的新节点。
过程：
1. 找到第 i-1个节点 p（即要插入位置的前驱节点）。
2. 创建新节点 s。
3. 调整指针：s->next = p->next;s->prior = p;p->next->prior = s;p->next = s;。
关键点：需要处理 p->next可能为 NULL的情况（即插在表尾），此时无需执行 p->next->prior = s;。
时间复杂度：平均 O(n)，因为需要遍历寻找位置。

删除第i个位置元素，算法如下：

bool ListDelete(DLinkNode *&L,int i,ElemType &e)
{int j=0;DLinkNode *p=L,*q;if(i<=0)return false;while(j<i-1&&p!=NULL){j++;p=p->next;}if(p==NULL)return false;else{q=p->next;if(q==NULL)return false;e=q->data;p->next=q->next;if(q->next!=NULL)q->next->prior=p;free(q);return true;}
}

作用：删除双链表中第 i个位置的节点，并通过引用 e返回被删除节点的值。
过程：
1. 找到第 i-1个节点 p（即要删除节点的前驱节点）。
2. 用 q指向要删除的节点 (q = p->next)。
3. 保存值 e = q->data。
4. 调整指针：p->next = q->next;。如果 q->next不为 NULL，还需设置 q->next->prior = p;。
5. 释放节点 q的内存。
关键点：需要处理多种边界情况（i不合法、p为 NULL、q为 NULL）。
时间复杂度：平均 O(n)，因为需要遍历寻找位置。

两个应用示例

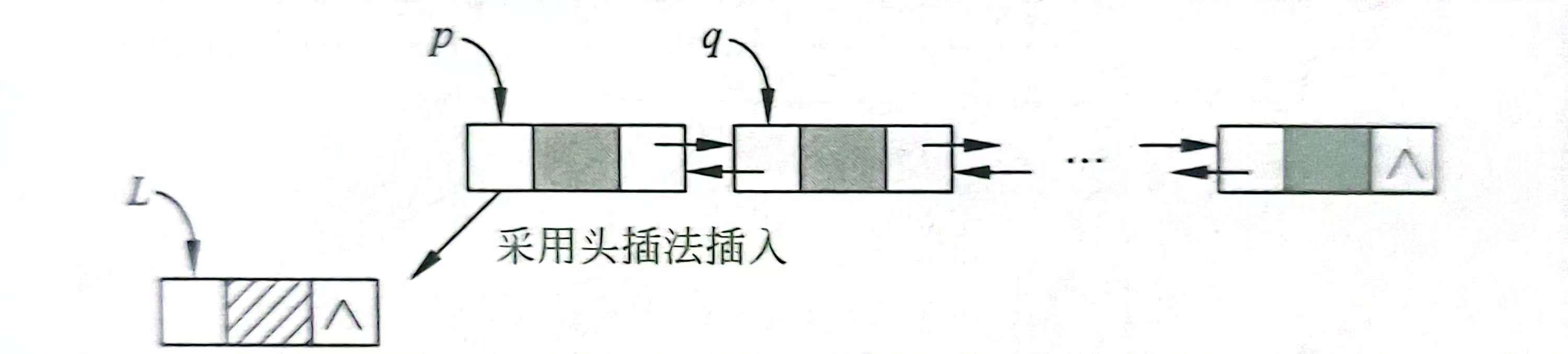
1.将一个带头双链表的所有元素倒置，具体算法如下：

void reverse(DLinkNode *&L)//整体建表法，链表倒置
{DLinkNode *NL=L,*p=L->next,*q;NL->next=NULL;while(p!=NULL){q=p->next;p->next=NL->next;if(NL->next!=NULL)NL->next->prior=p;p->prior=NL;NL->next=p;p=q;}
}

作用：将整个双链表逆置。
过程（头插法思想）：
1. 创建一个新链表 NL（其实是复用原头节点 L），初始化其 next为 NULL。
2. 依次遍历原链表的每一个节点 p（从第一个有效节点开始）。
3. 将 p从原链表中取下，然后总是将其插入到新链表 NL的头节点之后。
4. 遍历完成后，新链表 NL就是原链表的逆置。
通俗理解：像把一叠牌一张张拿起，然后放到另一叠上。拿起的顺序是A,B,C，放上去后新叠的顺序就是C,B,A。
时间复杂度：O(n)。

2.将一个双链表的所有数据结点按data域递增排序，具体算法如下：

void sort(DLinkNode *&L)//插入法，链表递增
{DLinkNode *p,*pre,*q;p=L->next->next;L->next->next=NULL;while(p!=NULL){q=p->next;pre=L;while(pre->next!=NULL&&pre->next->data<p->data)pre=pre->next;p->next=pre->next;if(pre->next!=NULL)pre->next->prior=p;p->prior=pre;pre->next=p;p=q;}
}

作用：使用直接插入排序的算法思想，将双链表按数据域的值递增排序。
过程：
1. 从第二个节点开始遍历 (p = L->next->next)。
2. 将当前节点 p从链表中取下。
3. 在已排序的序列（从头节点开始到 p的前一个节点）中，找到第一个比 p->data大的节点的前驱位置 pre。
4. 将 p插入到 pre之后。
通俗理解：像打扑克时抓牌，每抓一张新牌，就在已排好序的手牌中找到合适的位置插进去。
时间复杂度：O(n²)。

双链表 vs. 单链表：如何选择？

为了帮助你更好地决策，这个表格对比了它们的关键差异：

特性	双链表 (Doubly Linked List)	单链表 (Singly Linked List)
遍历方向	双向（前驱和后继）	单向（仅后继）
插入删除效率	高（已知位置时 O(1)）	较低（删除或前插常需 O(n) 找前驱）
内存开销	大（每个节点多一个指针）	小
实现复杂度	略高（需维护两个指针）	简单
边界处理	更简单（尤其带哨兵节点）	相对复杂