当前位置：首页 > news >正文

为你的数据选择合适的分布：8个实用的概率分布应用场景和选择指南

news 2025/9/19 8:23:18

拿到数据想建模，但不知道用哪个分布？大部分教科书都在讲一堆你永远用不到的东西。实际工作中，你只需要掌握几个核心分布，然后知道什么时候该用哪个就够了。

这里是我在做分析、实验设计、风险建模时真正会用的8个分布。每个都会告诉你使用场景、快速拟合方法、需要避开的坑，以及现成的代码。

伯努利分布：最基础的二元事件

点击还是不点击，欺诈还是正常，用户流失还是留存。单次试验的成功失败问题，用伯努利分布就对了。

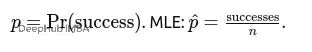
但是数据严重不平衡时别硬套伯努利，记得做校准处理。比如欺诈检测场景，正负样本比例差太多的话，直接用p估计会有偏。

 import numpy as np  
y = np.array([0,1,0,1,1,0,0,1])  
p = y.mean()            # MLE for Bernoulli  
samples = np.random.binomial(1, p, size=10000)

二项分布：多次试验的累计结果

用户看了10次广告点了几次？50封邮件打开了多少？这种"N次机会中成功K次"的场景，二项分布最合适。

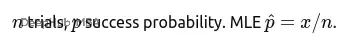
如果试验之间有关联（比如同一用户多次看广告），方差会比理论值大。这时候考虑用Beta-二项分布，能更好处理过度分散的情况。

 from scipy.stats import binom  
n, x = 50, 17  
p_hat = x / n  
ci = binom.interval(0.95, n, p_hat)  # simple CI on counts

泊松分布：计数事件的标配

每分钟客服电话、每小时系统故障、每平方米缺陷数。这些稀有且相互独立的计数事件，泊松分布处理起来最直接。

方差远大于均值的话，说明数据过度分散了。这种情况泊松分布就不够用，得换负二项分布（实际上是泊松和伽马的混合）。

 from scipy.stats import poisson  
counts = [0,1,0,2,1,0,3,1]  
lam = np.mean(counts)  
pmf = poisson.pmf(np.arange(6), lam)

正态分布：数据分析的主力

KPI的平均值、传感器噪声、大样本的误差分析。正态分布虽然被用烂了，但在合适的场景下确实好用。

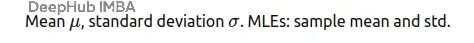
轻微偏斜或者有异常值的话，正态分布的估计就会偏。小样本或者明显厚尾的数据，直接上学生t分布更稳妥。

 from scipy.stats import norm  
mu, sigma = np.mean(counts), np.std(counts, ddof=1)  
cdf90 = norm.cdf(90, mu, sigma)

学生t分布：处理小样本和异常值

数据有明显的厚尾特征，或者样本量不够大？正态分布容易被异常值带偏，这时候t分布更靠谱。测量数据偶尔出现的异常峰值、小样本的均值估计，都适合用它。

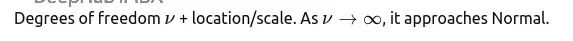
别把t分布当万能药。真的有严重异常值，还是得先清理数据或者做winsorizing处理，t分布只是比正态分布抗造一些。

 from scipy.stats import t  
nu = 5  
# probability a standardized value is within 2 std  
prob = t.cdf(2, df=nu) - t.cdf(-2, df=nu)

指数分布：等待时间建模

用户点击通知后多久会打开APP？系统两次故障之间间隔多久？只要是"等待第一次事件发生"的时间建模，而且事件发生率恒定，指数分布就很合适。

率参数λ，均值是1/λ。

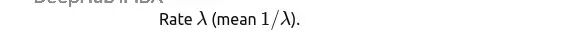
 from scipy.stats import expon  
lam = 0.2  
samples = expon(scale=1/lam).rvs(10000)   # mean ≈ 1/lam

对数正态分布：处理乘性过程

用户会话时长、单用户收入、文件大小这些数据往往是多个正数因子相乘的结果。如果把数据取对数后看起来接近正态分布，那对数正态分布就是你要的。

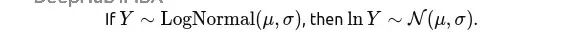
尾部数据会严重拖累均值，做报告或者假设检验时用中位数和几何均值更稳定。

 from scipy.stats import lognorm  
sigma, mu = 0.8, 1.2  
rv = lognorm(s=sigma, scale=np.exp(mu))  
q95 = rv.ppf(0.95)

Beta分布：概率的概率

要建模转化率、缺陷率、分类器召回率这些本身就是概率的量？Beta分布天生就是干这个的。配合二项数据做贝叶斯推断特别好用。

α和β太小的话分布会很尖锐。做先验设置时要合理，比如α=β=1是均匀分布，α=β=2是相对温和的先验。

 from scipy.stats import beta  
alpha0, beta0 = 2, 2  
x, n = 17, 50  
posterior = beta(alpha0 + x, beta0 + (n - x))  
credible = posterior.interval(0.95)   # 95% credible interval for p

快速选择合适的分布

遇到具体问题，按这个思路走基本不会有错：

二元结果直接伯努利。N次试验中成功K次用二项，不过如果方差明显大于理论值就换Beta-二项。计数类型的用泊松，过度分散就上负二项。

均值类的数据优先考虑正态，有厚尾或者样本小就用t分布。等待时间且发生率恒定选指数，发生率会变化就考虑韦伯分布。

正数且明显右偏的数据试试对数正态，或者你想直接控制均值和形状参数的话用伽马分布也行。要建模概率本身，Beta分布是唯一选择。

拟合验证的技巧

别急着套公式，先画图。直方图能立刻告诉你数据的偏斜程度和异常情况，对数直方图对于长尾数据特别有用。

参数估计用最大似然或者矩估计都行，但是一定要用残差图和QQ图验证拟合效果。信息准则AIC/BIC比较不同分布的优劣，或者简单点用留出集的对数似然。

最重要的是模拟验证。用拟合好的分布生成数据，看看均值、方差、分位数是不是和原始数据对得上。如果对不上，说明这个分布选错了，哪怕拟合图看起来很漂亮也没用。

下面是通用代码模板

import numpy as np  
import pandas as pd  
from scipy import stats 
def fit_and_score(sample, candidate):  params = candidate.fit(sample)       # generic MLE  ll = np.sum(candidate.logpdf(sample, *params))  k = len(params)  aic = 2*k - 2*ll  return params, aic  data = np.array([...], dtype=float)  
cands = [stats.norm, stats.t, stats.lognorm, stats.gamma]  
scores = [(c.name, *fit_and_score(data, c)) for c in cands]  
best = min(scores, key=lambda r: r[-1])  # lowest AIC