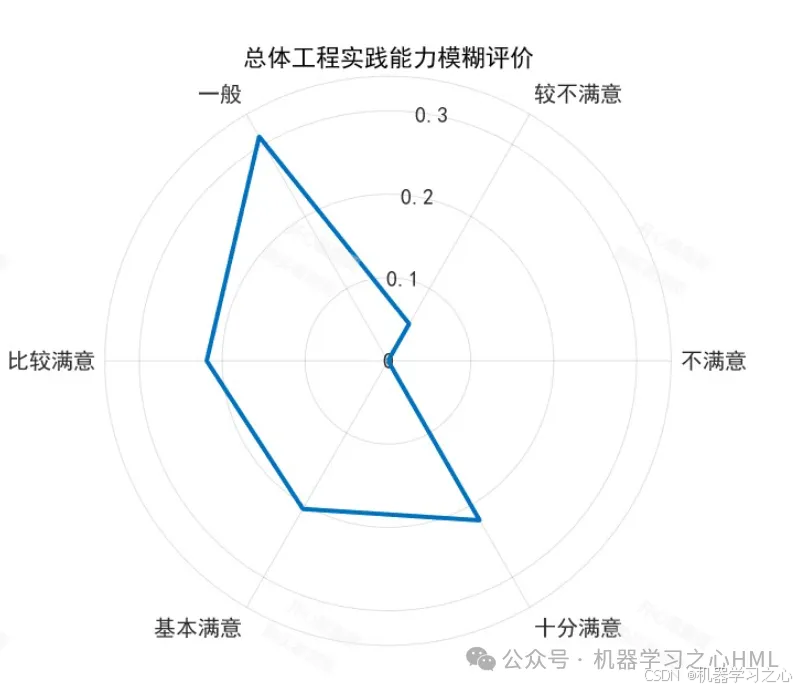
MATLAB基于AHP-模糊综合评价法的工程实践能力评价

---

一、 方法概述

该方法结合了层次分析法（AHP） 和模糊综合评价法两种模型的优点，形成一个强大的评价体系。

• AHP (Analytic Hierarchy Process) - 主观赋权：

  • 作用： 将复杂的“工程实践能力”评价问题层次化，通过构造判断矩阵，计算出各级评价指标（如专业能力、沟通能力、安全意识等）的权重。它解决了“哪个指标更重要”的问题。
  • 特点： 将人的主观判断用数量形式表达和处理，具有系统性、简洁性、实用性的优点。

• 模糊综合评价法 (Fuzzy Comprehensive Evaluation) - 客观定量：

  • 作用： 利用模糊数学理论，处理评价中存在的模糊性和不确定性（如“较好”、“一般”、“较差”这类模糊评价语言）。它将定性评价转化为定量评价，最终得到一个清晰、可比较的评价结果。
  • 特点： 特别适合对难以精确定量、受多种因素影响的事物进行评价。

结合逻辑： 先用AHP科学地确定各评价指标的权重，再用模糊综合评价法对受多个因素影响的事物做出一个总体的、量化的评价。

---

二、 算法步骤与公式原理

第一步：建立评价指标体系（层次结构模型）

将“工程实践能力”这个总目标分解为若干一级指标（准则层），每个一级指标再分解为若干二级指标（方案层），形成一个树状层次结构。

示例：

• 目标层 (A): 工程实践能力综合评价
• 准则层 (B): B1 专业基础能力, B2 工程管理与协作能力, B3 创新与解决问题能力, B4 职业素养
• 指标层 ©:
  • C11 (隶属于B1): 理论知识掌握度
  • C12 (隶属于B1): 工具/软件操作熟练度
  • C21 (隶属于B2): 沟通表达能力
  • C22 (隶属于B2): 团队协作能力
  • … (以此类推)

第二步：AHP确定权重

1. 构造判断矩阵：
   邀请专家（或评价小组）对同一层次的指标进行两两比较，根据1-9标度法（如表所示）给出相对重要性比值，形成判断矩阵 (A)。

   标度	含义
   1	表示两个因素相比，具有同样重要性
   3	表示两个因素相比，一个因素比另一个因素稍微重要
   5	表示两个因素相比，一个因素比另一个因素明显重要
   7	表示两个因素相比，一个因素比另一个因素强烈重要
   9	表示两个因素相比，一个因素比另一个因素极端重要
   2,4,6,8	上述相邻判断的中间值

   示例：判断矩阵 $A-B$(准则层对目标层的判断矩阵)

   A	B1	B2	B3	B4
   B1	1	3	1/2	4
   B2	1/3	1	1/5	2
   B3	2	5	1	6
   B4	1/4	1/2	1/6	1

2. 计算权重向量并进行一致性检验：

   • 计算权重 (W)： 常用和积法或方根法。
     • 方根法步骤：
       1. 计算判断矩阵每行元素的几何平均数： ${\bar{w}}_i=\sqrt[n]{{\prod }_{j=1}^n{a}_{ij}}$
       2. 将 ${\bar{w}}_i$ 归一化得到权重向量 $W_i={\bar{w}}_i/{\sum }_{j=1}^n{\bar{w}}_j$
   • 一致性检验： 为确保判断逻辑自洽，必须进行一致性检验。
     1. 计算最大特征值 ${\lambda }_{\text{max}}$
     2. 计算一致性指标$CI=\frac{{\lambda }_{\text{max}}-n}{n-1}$
     3. 查询随机一致性指标 $RI$ (标准值)
     4. 计算一致性比率 $CR=\frac{CI}{RI}$
     • 当 $CR<0.1$ 时，认为判断矩阵的一致性是可以接受的，否则需要调整。

   此过程需从指标层->准则层->目标层逐层进行，最终得到所有指标相对于总目标的组合权重。

第三步：模糊综合评价

1. 确定评价集（评语集）V：
   设定可能的评价结果等级，如： V={V1,V2,V3,V4}={优秀,良好,一般,较差}V = \{ V1, V2, V3, V4 \} = \{\text{优秀}, \text{良好}, \text{一般}, \text{较差} \}V={V1,V2,V3,V4}={优秀,良好,一般,较差}

2. 构造模糊关系矩阵（隶属度矩阵）R：
   对最低层指标（如C11, C12…）进行评价。例如，由10位专家对某学生的“理论知识掌握度(C11)”进行评价，3人评“优秀”，5人评“良好”，2人评“一般”，0人评“较差”。则C11的隶属度向量为： $R_{11}=[0.3,0.5,0.2,0.0]$。
   为每一个最低层指标都构造这样的向量，组合成该指标所属上层指标的模糊关系矩阵 $R$。

3. 进行模糊合成运算：
   将AHP得到的权重向量 $W$ 与模糊关系矩阵$R$ 进行合成运算，得到对该上层指标的模糊评价结果向量 $B$。
   $$B=W\circ R=(w_1,w_2,...,w_n)\circ \left[\begin{array}{cccc}{r}_{11}& r_{12}& ...& r_{1m}\\ r_{21}& r_{22}& ...& r_{2m}\\ ...& ...& ...& ...\\ r_{n1}& r_{n2}& ...& r_{nm}\end{array}\right]=(b_1,b_2,...,b_m)$$
   其中“$\circ$”是合成算子，通常采用加权平均型算子（M(·, +)），即普通矩阵乘法$b_j={\sum }_{i=1}^n(w_i\cdot r_{ij}$

4. 多级模糊综合评价：
   从最底层指标开始向上逐层评价。将下一层的评价结果 (B) 作为上一层的模糊关系矩阵 (R) 的一部分，直至得到对总目标A的最终评价结果向量 $B_{\text{总}}$。

第四步：处理评价结果

得到的最终评价结果 $B_{\text{总}}$是一个模糊向量（如 [0.35, 0.40, 0.20, 0.05]），表示该学生的工程实践能力分别隶属于“优秀”、“良好”、“一般”、“较差”的程度。

• 最大隶属度原则： 选择向量中最大值对应的等级作为最终评价结果（如上例，结果为“良好”）。
• 加权平均法： 若评价集V是数值化的（如[95, 85, 70, 50]），可计算最终得分： $S=B_{\text{总}}\times V^T$，使结果更加精细。

---

三、 技术路线与工具实现

1. 技术路线：
   确立评价目标 -> 构建层次结构 -> 设计调查问卷 -> (专家评价) -> AHP计算权重 -> 一致性检验 -> 构建模糊矩阵 -> 多级模糊合成 -> 得出评价结果

2. 工具实现：

   • Excel： 非常适合进行AHP的矩阵计算、权重计算和一致性检验。可以使用公式和矩阵函数完成。
   • MATLAB / Python：
     • AHP部分： 可以编程实现判断矩阵的输入、权重计算和一致性检验的自动化。
     • 模糊评价部分： 可以轻松实现矩阵运算，特别是多级评价时，代码比Excel更清晰。
   • 专业软件： yaahp、Super Decisions等软件提供了图形化界面来完成AHP和模糊综合评价的全过程。

---

四、 方法特点

• 优点：

  1. 系统性： 将定性分析与定量分析结合，结果科学、系统。
  2. 包容性： 能有效处理评价中的模糊性和主观性。
  3. 实用性： 原理简单明了，易于理解和操作，适用面广。

• 缺点：

  1. 主观性： AHP的判断矩阵依赖于专家的主观经验，专家水平直接影响结果质量。
  2. 复杂性： 当指标过多时，判断矩阵的数量会急剧增加，工作量大，且不易保持一致性。
  3. 静态性： 评价模型一旦建立，难以随环境变化而动态调整。

总而言之，AHP-模糊综合评价法是评价像“工程实践能力”这类复杂、多因素、模糊问题的强大工具。只要科学地设计指标体系并谨慎地组织专家评判，就能得到令人信服的评价结果。

代码私信回复MATLAB基于AHP-模糊综合评价法的工程实践能力评价