线性分组码及其相关概念

        发送端发送的数字信息在信道中传输时由于噪声的影响会发生码元出错的问题，码元出错会导致接收端不能正确的获得发送端发送的数据。

        对发送的数字信息进行信道编码，通过添加一部分冗余信息可以使发送的码字具有纠错检错的能力。
将发送的信息序列进行分段，每段包含k 个信息位，将这k 个信息位通过一定的规则产生r个校验位，形成长为n= k+r的一组码字，这种码字叫做(n,k)分组码，其中R=k/n称为码率，表示(n,k) 分组码中信息位所占的比重。

当通过一定规则生成的校验位与信息位具有线性关系时，这种码字叫做线性分组码。

        在二元域上，(n,k)线性分组码中每个码元的取值为 0 或 1，所以n个码元可以组成 种向量c ，这些向量组成的向量空间记为 。(n,k)线性分组码是向量空间的一个k维子空间，所以(n,k) 线性分组码中的码字c完全可以由k个线性独立的n维向量线性表示

        其中，表示k个信息位码元。k个线性独立的n维向量分别为

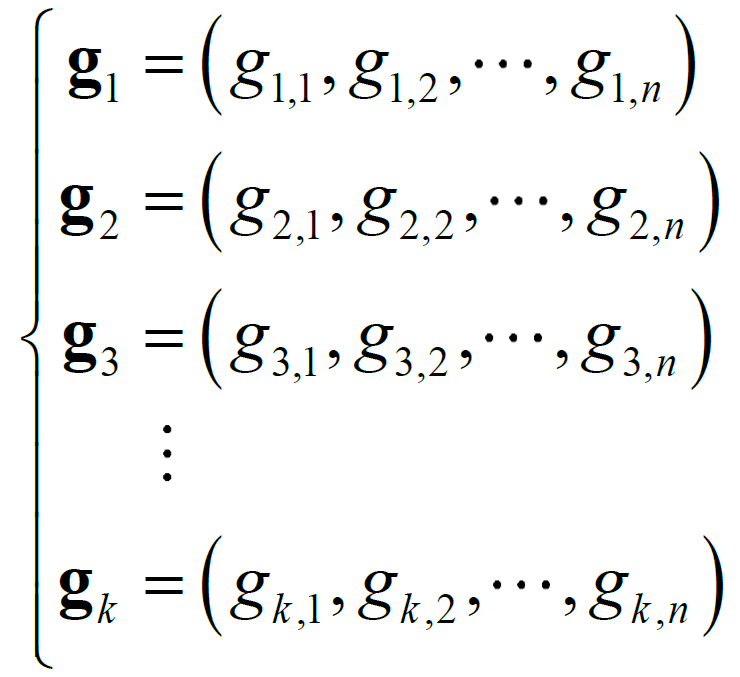
        写成矩阵的形式，则有

        令k 个信息位码元组成的向量记为，那么上式可以写成

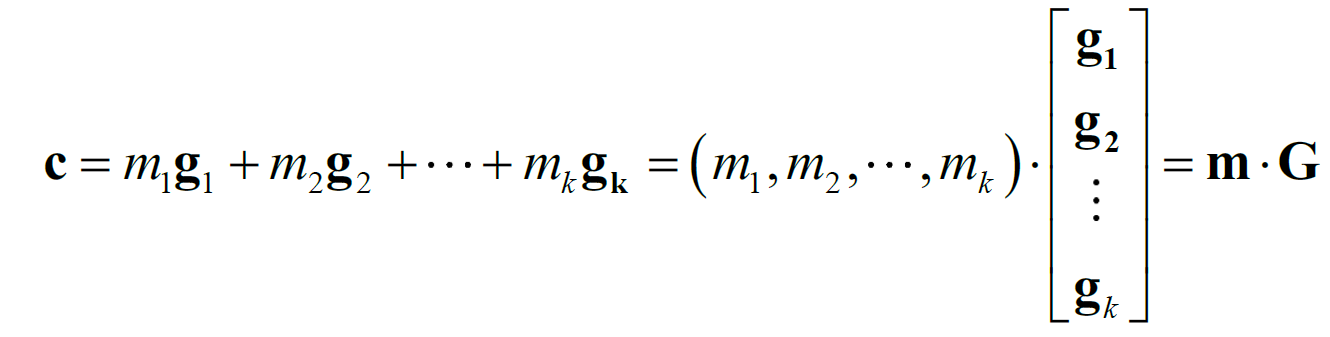
        由上式可以看出，通过对矩阵G中的行向量按照码元向量m中的元素在二元域中线性组合，即信息向量m与矩阵G相乘即可得到线性分组码中的码字c ，这个过程即为(n,k) 线性分组码的编码过程，其中矩阵G称为(n,k) 线性分组码的生成矩阵。
对于(n,k) 线性分组码来说，存在矩阵H，维度为(n-k) *n，其每个行向量线性独立且与生成矩阵G 中每个行向量正交。所有与矩阵H的行向量正交的向量全部存在于生成矩阵G中行向量生成的空间。矩阵H称为(n,k) 线性分组码的校验矩阵。因为(n,k) 线性分组码可以通过生成矩阵G的任意行向量线性组合生成，所以(n,k) 线性分组码也与校验矩阵H的行向量正交，即有

        其中c为(n,k) 分组码的一个码字，H为(n,k) 分组码的校验矩阵。这种特性使得可以通过将接收码字与校验矩阵的转置相乘来判断接收码字是否完全正确，这在线性分组码译码的过程中发挥着重要的作用。