矩阵的导数运算

---

前言

本系列是个人在b站大学学习【DR_CAN】的最优控制教程的笔记，主要用于记录和方便随时知识回顾。

感谢DR_CAN精彩的讲解，附bilibili视频链接：【最优控制-合集】

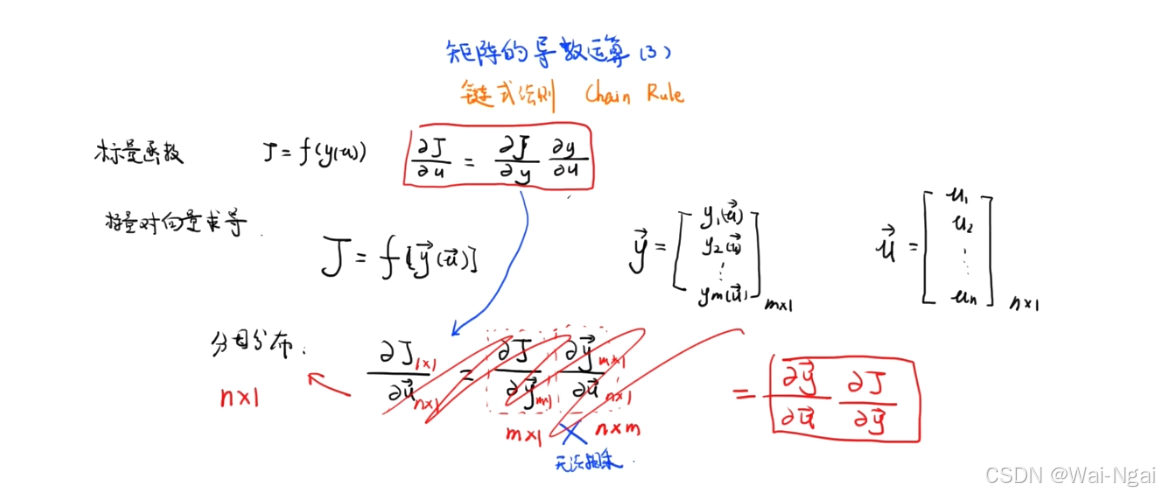
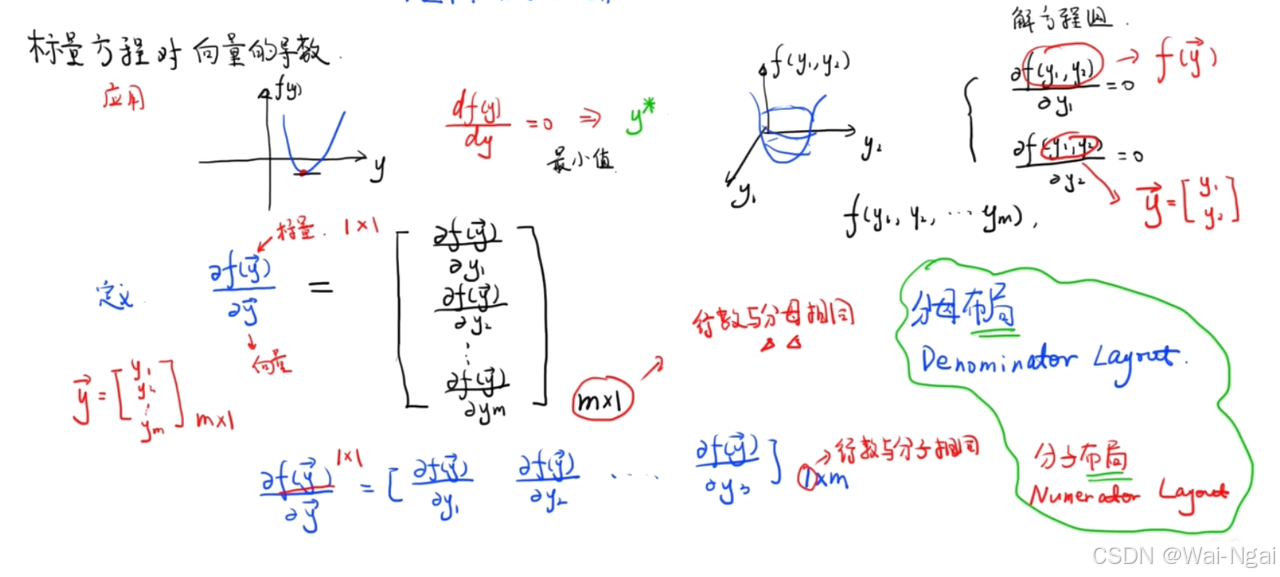
1. 标量方程对向量的导数

对于多元函数求极值问题，最常用的做法是分别求函数$f$对每一个自变量的偏导，然后组成偏导数的方程组，求解这个方程组。

如果我们将该函数的每个自变量组成一个向量$\vec{y}$，求函数f对向量$\vec{y}$的导数，即求一个标定方程对向量的导数。

这里有分母布局和分子布局两种形式，说白了就是最后的导数到底怎么排列的问题。更明白一点：最后导数矩阵的第一行到底是先对向量$\vec{y}$中的每一个变量都求一遍（分子布局），还是先只对第一个变量求一遍（分母布局）。

• 分子布局：导数的行数与分子的行数相同；
• 分母布局：导数的行数与分母的行数相同。这两种布局形式互为转置。

例子：

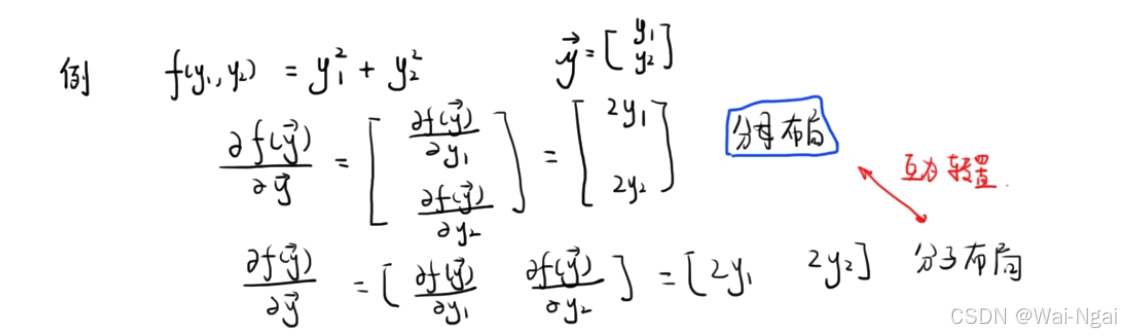
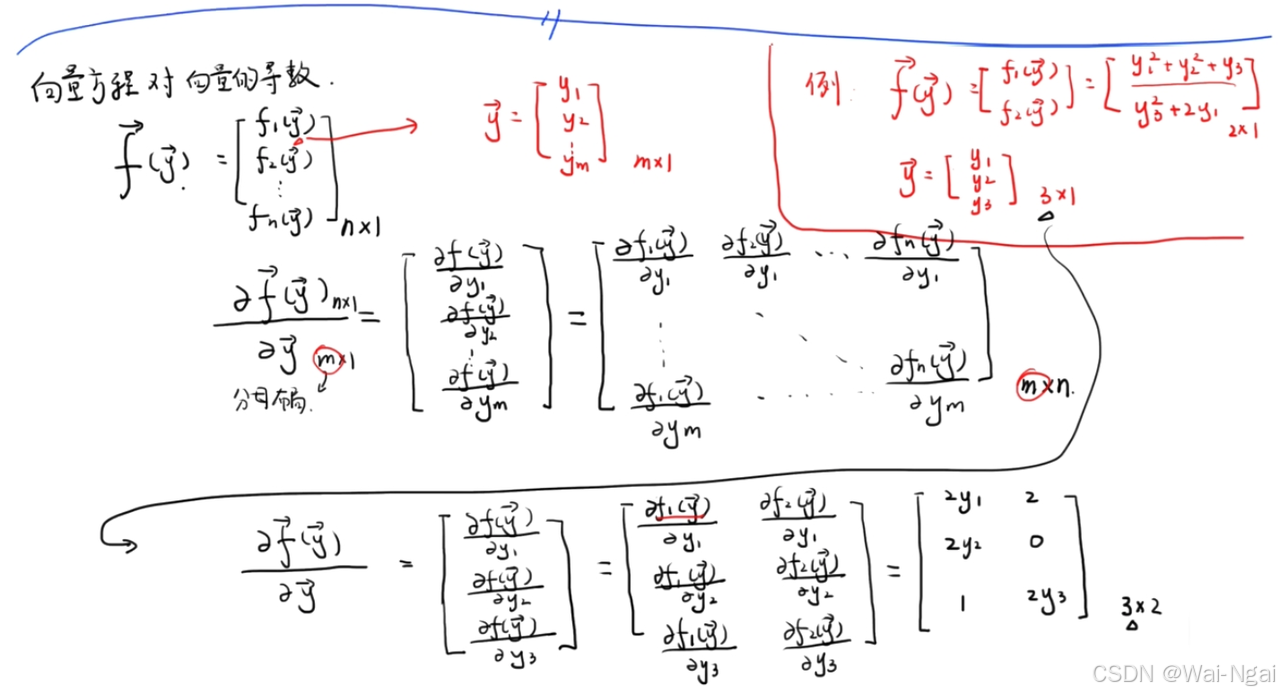
2. 向量方程对向量的导数

下面都采用分母布局，即最后导数矩阵的行数与分母的行数一致。

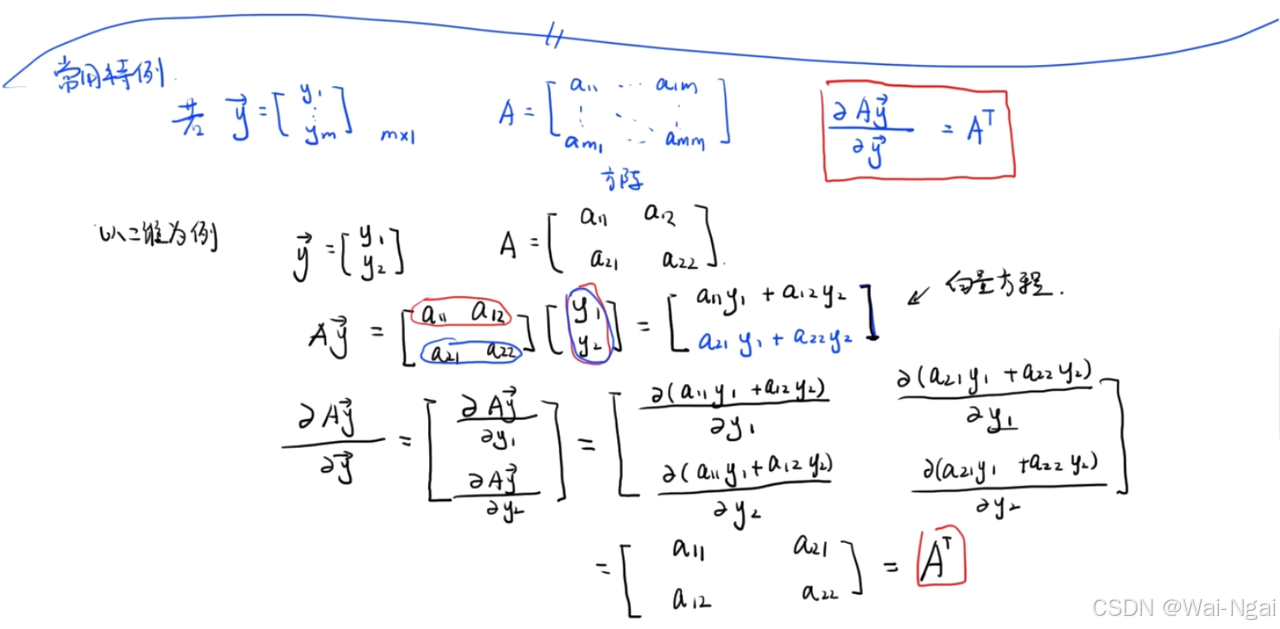
2.1 特例： $\frac{\partial A\vec{y}}{\partial \vec{y}}=A^T$

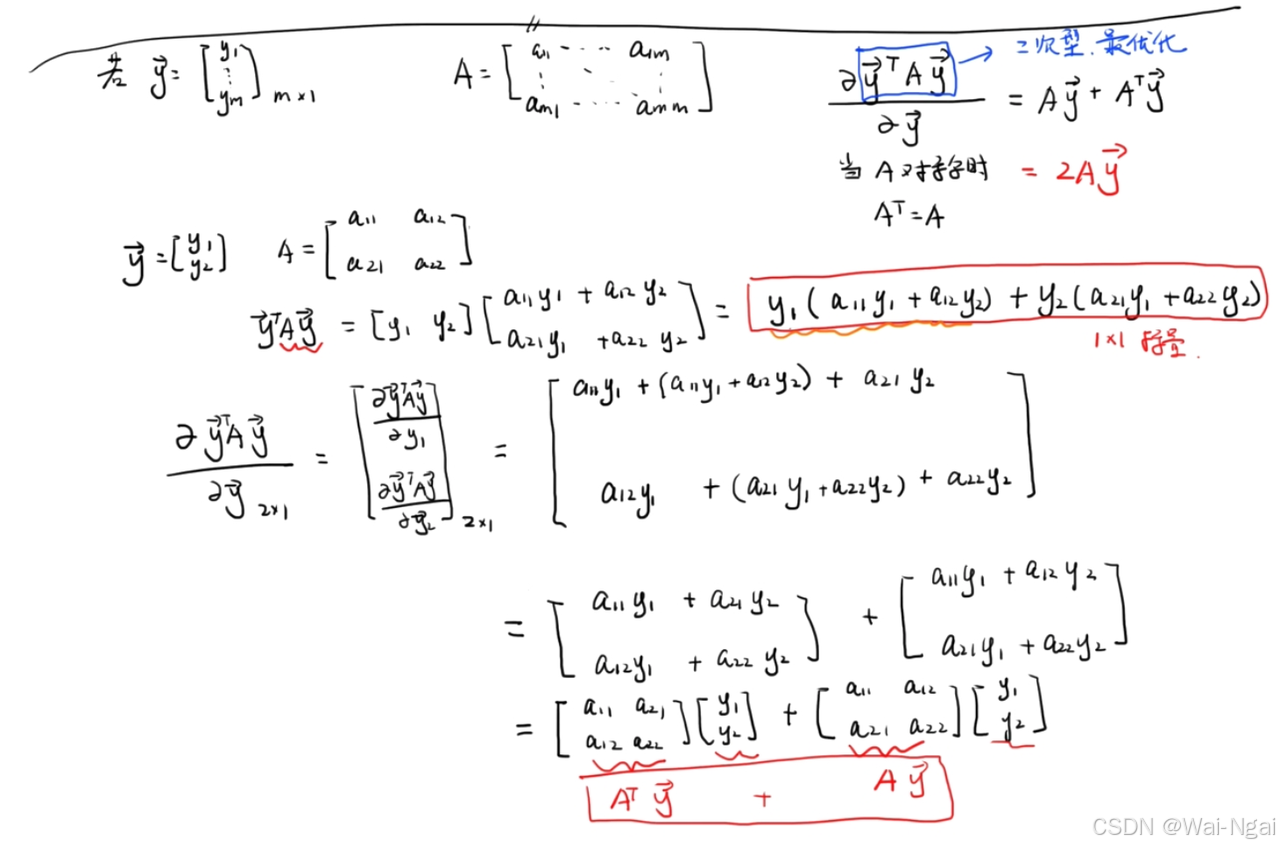
2.2 特例： $\frac{\partial {\vec{y}}^{T}A\vec{y}}{\partial \vec{y}}=A\vec{y}+A^T\vec{y}$

例子：

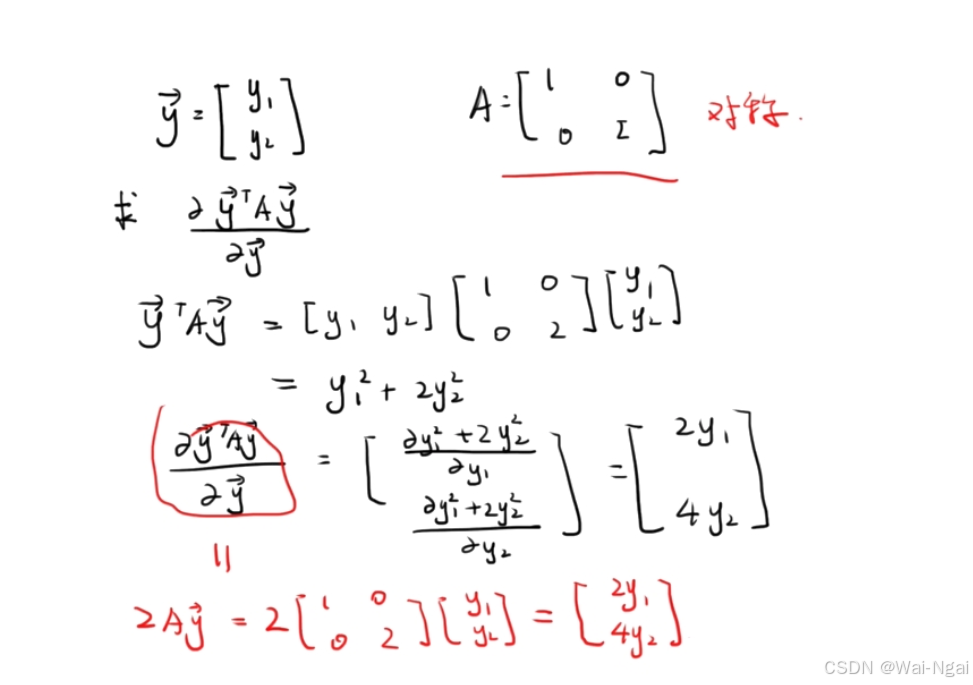
3. 链式法则

导数求导的链式法则。