滑动窗口法的优化与实战——力扣209.长度最小的子数组
力扣209.长度最小的子数组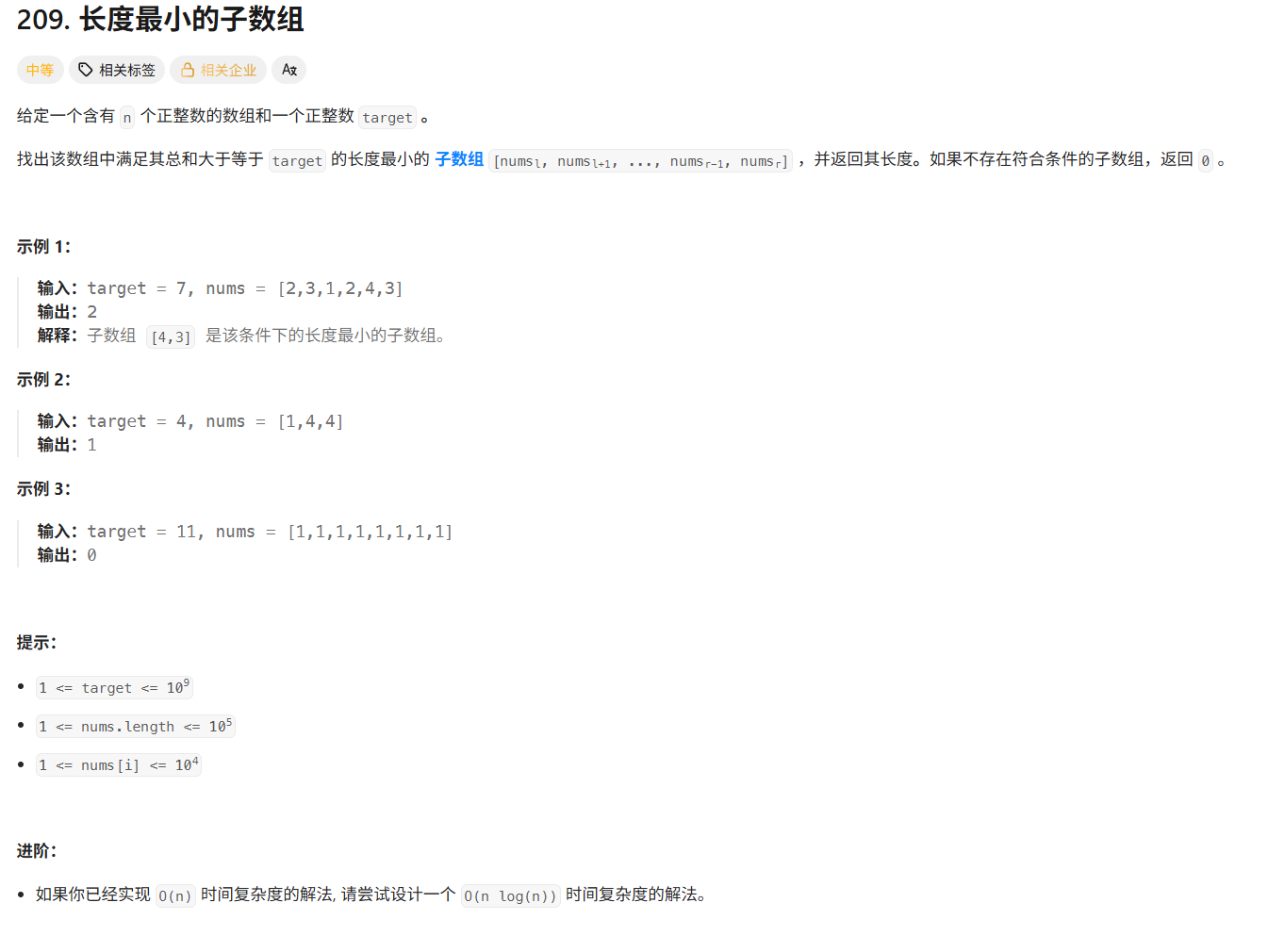
题目解析
给定一个正整数数组 nums 和一个目标值 target,找出满足其总和大于等于 target 的最短连续子数组的长度。如果不存在符合条件的子数组,返回 0。
我的初始代码(滑动窗口法)
初步思路
我一开始尝试用双指针 left 和 right 维护一个滑动窗口。初始化时,numbers = nums[left] 表示当前窗口的总和。当总和小于 target 时,右移 right 并累加;当总和大于等于 target 时,记录当前窗口长度,并左移 left 收缩窗口。
初始代码
class Solution {public int minSubArrayLen(int target, int[] nums) {int left = 0, right = 0;int minCount = nums.length + 1;int numbers = nums[left];if (numbers >= target) {return 1;}while (left < nums.length) {if (right < nums.length && numbers < target) {if (++right < nums.length) {numbers += nums[right];} else {break;}continue;}if (right < nums.length && numbers >= target) {minCount = minCount < right - left + 1 ? minCount : right - left + 1;numbers -= nums[left++];}if (minCount == 1) {return 1;}}if (minCount > nums.length) {return 0;}return minCount;}
}
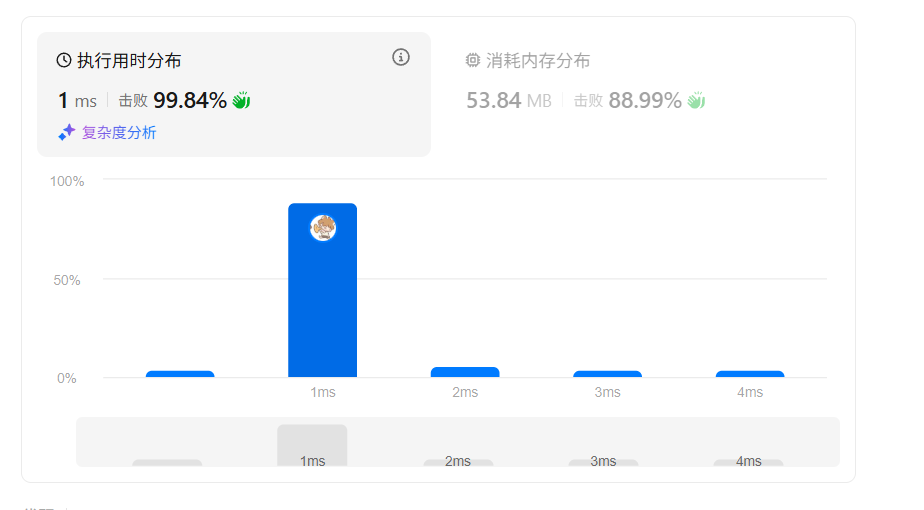
但这里有个问题:每次只收缩一次窗口,可能遗漏更短的子数组。
优化后的滑动窗口法
思路改进
意识到问题后,我决定调整窗口收缩逻辑:只要总和仍大于等于 target,就持续左移 left,直到总和不再满足条件。这样可以确保每次找到最小的窗口长度。
优化后的代码
class Solution {public int minSubArrayLen(int target, int[] nums) {int left = 0;int sum = 0;int minLength = Integer.MAX_VALUE;for (int right = 0; right < nums.length; right++) {sum += nums[right]; // 扩展窗口// 持续收缩窗口while (sum >= target) {int windowLength = right - left + 1;minLength = Math.min(minLength, windowLength);sum -= nums[left];left++;}}return minLength == Integer.MAX_VALUE ? 0 : minLength;}
}
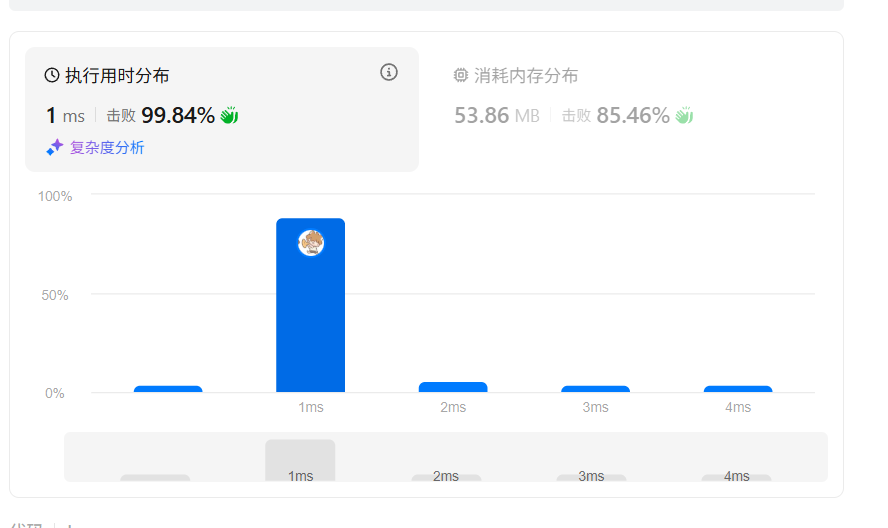
改进点
- 持续收缩窗口:通过
while循环不断左移left,直到总和小于target,确保所有可能的最短窗口都被覆盖。 - 逻辑简化:去除了复杂的
if-else分支,代码更易读。 - 边界处理:使用
Integer.MAX_VALUE初始化minLength,避免额外判断。
其他可行解法
前缀和 + 二分查找
- 思路:构建前缀和数组,对每个右端点,用二分查找寻找最小的左端点。
- 适用场景:正整数数组,需
O(n log n)解法。 - 代码:
java
class Solution {public int minSubArrayLen(int target, int[] nums) {int n = nums.length;int[] prefixSum = new int[n + 1];// 构建前缀和数组for (int i = 1; i <= n; i++) {prefixSum[i] = prefixSum[i - 1] + nums[i - 1];}int minLen = Integer.MAX_VALUE;for (int right = 1; right <= n; right++) {int s = prefixSum[right] - target; int leftIndex = binarySearch(prefixSum, s, 0, right); if (leftIndex != -1) {minLen = Math.min(minLen, right - leftIndex);}}return minLen == Integer.MAX_VALUE ? 0 : minLen;}// 二分查找:找最大的 left 使得 prefixSum[left] <= sprivate int binarySearch(int[] prefixSum, int s, int left, int right) {int res = -1;while (left <= right) {int mid = left + (right - left) / 2;if (prefixSum[mid] <= s) {res = mid; // 记录满足条件的索引left = mid + 1; // 继续向右找更大的 left} else {right = mid - 1;}}return res;}
}
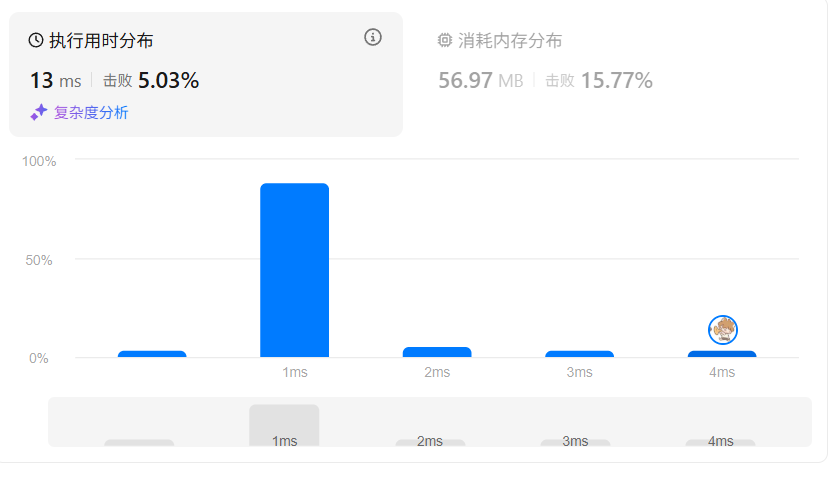
暴力解法(不推荐)
- 思路:遍历所有子数组,计算其和。
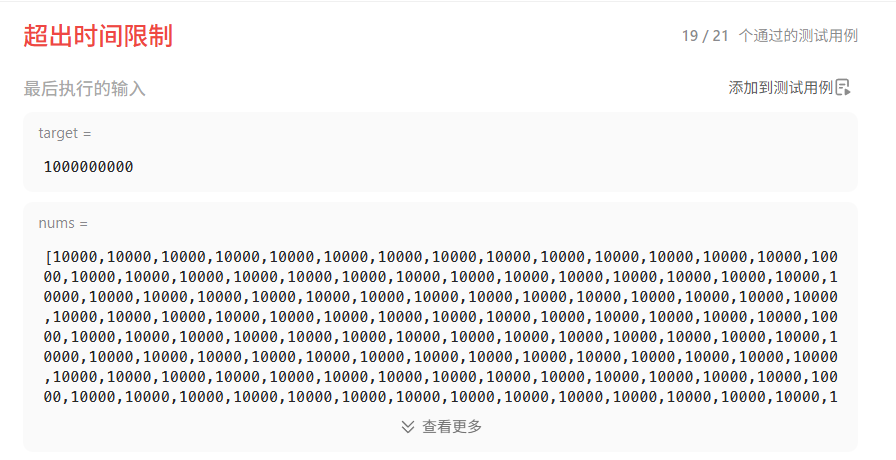
- 缺点:时间复杂度
O(n²),仅适用于小规模数据。 - 代码:
class Solution {public int minSubArrayLen(int target, int[] nums) {int n = nums.length;int minLen = Integer.MAX_VALUE;for (int i = 0; i < n; i++) {int sum = 0;for (int j = i; j < n; j++) {sum += nums[j];if (sum >= target) {minLen = Math.min(minLen, j - i + 1);break;}}}return minLen == Integer.MAX_VALUE ? 0 : minLen;}
}
总结与对比
| 方法 | 时间复杂度 | 空间复杂度 | 是否推荐 | 适用场景 |
|---|---|---|---|---|
| 初始代码(滑动窗口) | O(n) | O(1) | ⚠️ | 单次窗口收缩,逻辑较复杂 |
| 优化后滑动窗口法 | O(n) | O(1) | ✅ | 最优解,所有正整数数组通用 |
| 前缀和 + 二分查找 | O(n log n) | O(n) | ⚠️ | 正整数数组,需 O(n log n) 解法 |
| 暴力解法 | O(n²) | O(1) | ❌ | 小规模数据(n ≤ 10³) |
最终建议
滑动窗口法 是本题的首选解法。通过持续收缩窗口,可以高效地找到最短子数组,且时间复杂度为 O(n),空间复杂度为 O(1)。对于其他场景(如包含负数或需要 O(n log n) 解法),可考虑前缀和 + 二分查找。
