当前位置：首页 > news >正文

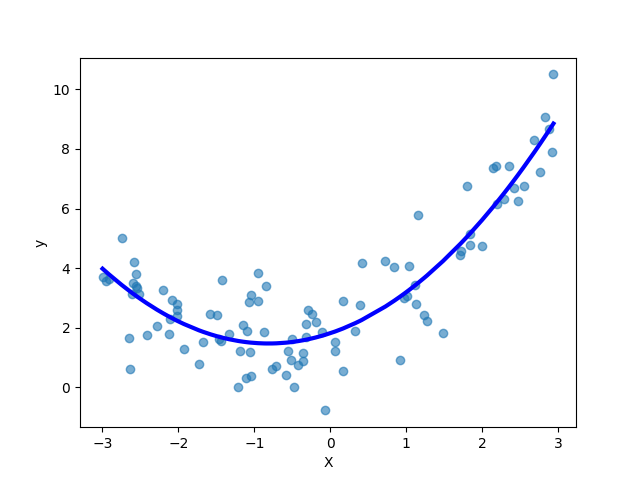
机器学习实战·第四章训练模型（1）

news 2025/9/18 19:26:00

一、线性回归

线性回归（Linear Regression）是机器学习中最基础、最核心的回归算法之一，核心目标是建模 “自变量” 与 “因变量” 之间的线性关系，并通过这种关系对未知的因变量进行预测。它既是入门机器学习的 “敲门砖”，也是许多复杂算法（如逻辑回归、神经网络）的基础思想来源。线性回归的本质是 “数据拟合”—— 从一堆杂乱的观测数据中，找到一条能最大程度反映数据趋势的直线（或高维空间中的 “超平面”）。

1.1 线性回归模型预测

1.2 线性回归的向量化形式

1.3 线性回归模型的MSE成本函数

MSE 是 “模型拟合效果的量化指标”——MSE 越小，说明模型预测值与真实值的整体差距越小，拟合效果越好。训练线性回归模型，就是要找到一组参数 $\theta$ ，使得这个 MSE 成本函数的值最小。

二、标准方程

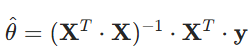
2.1 矩阵乘法

1、乘法前提：维度必须匹配

2、元素计算：行乘列求和

2.2 预测各参数的最优权重

# 导入NumPy库，用于高效的数组和矩阵运算（线性回归核心依赖矩阵操作）
import numpy as np# 生成特征数据X：100个样本，1个特征
# np.random.rand(100, 1)生成[0,1)区间的随机数，形状为(100,1)
# 乘以2后，X的取值范围变为[0,2)，模拟实际场景中的连续特征（如面积、时长等）
X = 2 * np.random.rand(100, 1)# 生成目标值y：基于真实"特征X与目标y的真实关系"并加入噪声
# 1. 真实线性关系为：y = 4 + 3*X（对应理论参数θ₀=4，θ₁=3）
# 2. 加入噪声项np.random.randn(100, 1)：符合标准正态分布（均值0，方差1）的随机扰动
#    模拟现实中无法预测的随机因素（如测量误差、未考虑的次要特征等）
y = 4 + 3 * X + np.random.randn(100, 1)# 构造扩展特征矩阵X_b（b代表bias，偏置项）
# 1. np.ones((100, 1))生成全为1的列向量，对应线性回归中的x₀=1（用于与偏置项θ₀相乘）
# 2. np.c_[]将全1列与原始特征X按列拼接，形成(100, 2)的矩阵
#    最终X_b的结构：第1列全为1，第2列为原始特征X
X_b = np.c_[np.ones((100, 1)), X]# 使用标准方程计算最优参数θ（theta_best）
# 标准方程公式：θ = (Xᵀ·X)⁻¹ · Xᵀ · y
# 分步解析：
# 1. X_b.T：对特征矩阵X_b求转置（得到Xᵀ）
# 2. X_b.T.dot(X_b)：计算Xᵀ与X的矩阵乘积（得到Xᵀ·X）
# 3. np.linalg.inv(...)：对上述结果求逆矩阵（得到(Xᵀ·X)⁻¹）
# 4. 依次与X_b.T（Xᵀ）和y相乘，最终得到最优参数向量θ
theta_best = np.linalg.inv(X_b.T.dot(X_b)).dot(X_b.T).dot(y)# 输出计算得到的最优参数
# 理论上应接近真实值θ₀=4，θ₁=3（因噪声存在会有小幅偏差）
print("最优参数θ（theta_best）：")
print(theta_best)

代码中生成目标值 y 时，加入了随机噪声 np.random.randn(100, 1)（正态分布、均值为 0 的噪声）。这意味着模型拟合的是 “带噪声的观测数据”，而非完全纯净的线性关系 y = 4 + 3X。由于噪声的存在，模型估计的参数（ ${\theta_{0} }$ =3.71和 $\hat{\theta_{1} }$ =3.13）会接近但不完全等于真实值（4 和 3），这是符合预期的（真实世界的数据几乎都带有噪声，模型需要拟合 “观测到的带噪声数据”）。

2.3 使用最优权重预测

(接上)
# 定义新的样本数据X_new，用于预测（共2个样本）
# 取值为0和2，覆盖原始特征X的取值范围[0,2)，便于观察预测趋势
X_new = np.array([[0], [2]])# 构造新样本的带偏置项特征矩阵X_new_b
# 结构与训练时的X_b一致：第一列全为1，第二列为新样本特征
# 形状为(2,2)，确保与theta_best（2,1）的矩阵乘法维度匹配
X_new_b = np.c_[np.ones((2, 1)), X_new]# 计算新样本的预测值y_predict
# 预测公式：y_hat = X_new_b · θ（矩阵点积，等价于线性回归的预测规则）
y_predict = X_new_b.dot(theta_best)# 输出预测结果
# 结果为2个值，分别对应X_new=[0]和X_new=[2]时的预测值
print(y_predict)

2.4 绘制模型预测结果

# 导入matplotlib的pyplot模块（通常需要在代码开头添加此行，否则会报错）
import matplotlib.pyplot as plt....# 绘制预测直线：用红色实线连接新样本的预测点，展示模型的线性拟合趋势
# X_new：新样本的特征值（[0, 2]），作为x轴数据
# y_predict：新样本的预测值，作为y轴数据
# 'r-'：格式字符串，'r'表示红色，'-'表示实线
plt.plot(X_new, y_predict, 'r-')# 绘制原始数据点：用蓝色圆点展示训练数据的分布，直观对比模型与真实数据的关系
# X：原始训练数据的特征，作为x轴数据
# y：原始训练数据的目标值，作为y轴数据
# 'b.'：格式字符串，'b'表示蓝色，'.'表示圆点标记
plt.plot(X, y, 'b.')# 设置坐标轴的显示范围，让图形更美观，聚焦于数据分布区域
# [0, 2, 0, 15]：依次表示x轴最小值、x轴最大值、y轴最小值、y轴最大值
# 这里x轴范围与X_new的取值（0和2）匹配，y轴范围覆盖预测值和原始数据的大致区间
plt.axis([0, 2, 0, 15])# 显示图形：触发matplotlib的绘图窗口，展示上述绘制的所有元素（直线和散点）
plt.show()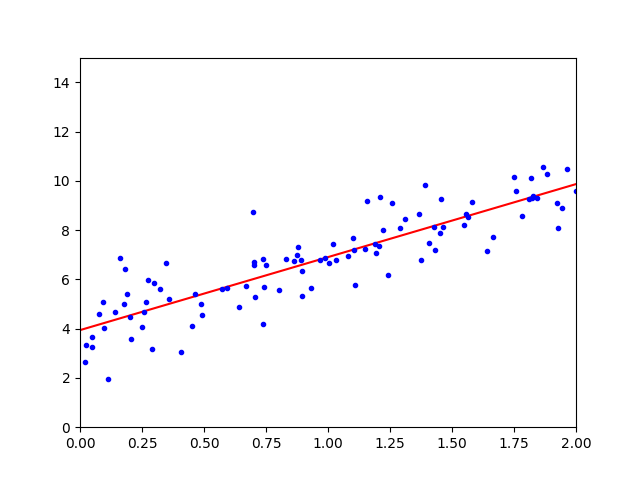

当执行 plt.plot(X_new, y_predict, 'r-') 时：
Matplotlib将 X_new 视为 x 坐标值：[0, 2]
Matplotlib将 y_predict 视为 y 坐标值：[y₁, y₂]（其中 y₁ 和 y₂ 是对应于 x=0 和 x=2 的预测值）
使用红色直线 ('r-') 连接这两个点 (0, y₁) 和 (2, y₂)

2.5 使用Scikit-Learn的等效代码

# 导入必要的库
import numpy as np  # 用于生成和处理数值数组
from matplotlib import pyplot as plt
from sklearn.linear_model import LinearRegression  # 导入scikit-learn中的线性回归模型类# 生成模拟的特征数据X
# np.random.rand(100, 1)生成100行1列的随机数（范围[0,1)）
# 乘以2后，X的取值范围变为[0,2)，模拟实际场景中的连续特征（如面积、时长等）
X = 2 * np.random.rand(100, 1)# 生成模拟的目标值y（带噪声的线性关系）
# 1. 真实的线性关系为：y = 4 + 3*X（对应理论参数：截距θ₀=4，斜率θ₁=3）
# 2. 加入噪声项np.random.randn(100, 1)：符合标准正态分布（均值0，方差1）的随机扰动
#    模拟真实世界中无法避免的测量误差或未考虑的影响因素
y = 4 + 3 * X + np.random.randn(100, 1)# 初始化线性回归模型
# LinearRegression()会自动处理偏置项（无需手动添加全1列），内部使用高效算法求解最优参数
lin_reg = LinearRegression()# 训练模型（拟合数据）
# fit(X, y)方法会根据输入的特征X和目标值y，计算使均方误差最小的最优参数（θ₀和θ₁）
lin_reg.fit(X, y)# 输出模型学习到的参数
# coef_：存储特征的权重（斜率θ₁），是一个二维数组（因可能有多个特征）
# intercept_：存储偏置项（截距θ₀），是一个一维数组
# 由于数据存在噪声，参数值会接近理论值（θ₀≈4，θ₁≈3）但不完全相等
print("偏置项（θ₀）：", lin_reg.intercept_)
print("特征权重（θ₁）：", lin_reg.coef_)# 定义需要预测的新样本
# X_new包含两个样本，特征值分别为0和2（覆盖原始特征X的取值范围[0,2)）
# 注意：scikit-learn要求输入必须是二维数组（即使只有1个特征），因此用[[0], [2]]而非[0, 2]
X_new = np.array([[0], [2]])# 使用训练好的模型预测新样本的目标值
# predict方法会根据学习到的参数计算：y_pred = θ₀ + θ₁×X_new
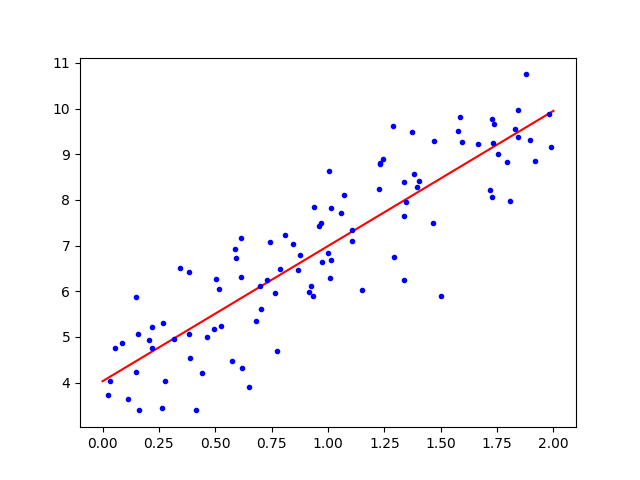
print("新样本的预测值：", lin_reg.predict(X_new))plt.plot(X_new, lin_reg.predict(X_new),'r-')
plt.plot(X,y,'b.')
plt.show()

三、梯度下降

3.1 梯度下降

梯度下降是一种迭代式的优化算法，核心目的是通过不断调整模型参数（如线性回归中的 $\theta$ ），使 “成本函数”（如均方误差 MSE）达到最小值。可以结合 “山间找山脚” 的比喻和技术细节来理解：

想象你在大雾笼罩的山上，看不到山脚（成本函数的全局最小值），但能感知脚下的坡度（梯度）。为了最快到达山脚，你会选择沿着 “最陡的下坡方向” 一步步走—— 这就是梯度下降的核心思想：沿着成本函数下降最快的方向（梯度的反方向）调整参数。

以线性回归的 “最小化 MSE” 为例，梯度下降的过程如下：

随机初始化参数：先给模型参数（如截距 ${\theta_{0} }$ )、斜率 ${\theta_{1} }$ ）一个随机初始值（相当于 “随机站在山上某位置”）。
计算梯度（局部坡度）：梯度是 “成本函数对参数的导数”，它反映两个关键信息：
- 变化率：当前位置的 “坡度多陡”（成本函数变化的快慢）；
- 变化方向：当前是 “上坡”（成本升高）还是 “下坡”（成本降低）。
沿梯度反方向调整参数：因为要让成本函数减小（下坡），所以需要往 “梯度的反方向” 移动参数。移动的 “步长” 由学习率（超参数）控制。
迭代直至收敛：重复 “计算梯度→调整参数” 的过程，直到梯度接近 0（此时到达 “山谷”，成本函数几乎不再下降），此时的参数就是使成本最小的最优参数。

3.2 学习率

学习率是控制 “每一步走多远” 的超参数，对收敛效果至关重要：

学习率太小：每一步移动距离过短，需要极多迭代才能到达最小值，训练速度极慢。
学习率太大：每一步移动距离过长，可能 “跳过” 山谷（最小值点），甚至 “跑到山的另一边”（成本反而升高），导致算法发散（永远找不到最优参数）。

3.3 批量梯度下降

3.3.1 成本函数的偏导数

3.3.2 成本函数的梯度向量

3.3.3 梯度下降步长

# 导入NumPy库，用于高效的数组和矩阵运算（梯度下降依赖矩阵乘法实现向量化计算）
import numpy as np# 生成特征数据X：100个样本，1个特征，取值范围[0,2)
# np.random.rand(100,1)生成[0,1)的随机数，乘以2扩展到[0,2)，模拟实际特征（如面积、时长）
X = 2 * np.random.rand(100, 1)# 生成目标值y：基于真实线性关系y=4+3X，加入正态分布噪声（均值0，方差1）
# 模拟真实世界中带噪声的数据，使问题更贴近实际场景
y = 4 + 3 * X + np.random.randn(100, 1)# 构造带偏置项的特征矩阵X_b
# 第一列全为1（对应偏置项θ₀的特征x₀=1），第二列为原始特征X
# 形状为(100,2)，确保与参数向量θ（2,1）的矩阵运算兼容
X_b = np.c_[np.ones((100, 1)), X]# 定义梯度下降的超参数
eta = 0.1  # 学习率：控制每次参数更新的步长（步长过大会发散，过小会收敛慢）
n_iterations = 1000  # 迭代次数：足够多的迭代确保算法收敛到最优解
m = 100  # 样本数量：用于梯度计算中的均值化（避免样本量影响梯度大小）# 随机初始化参数θ（θ₀和θ₁）
# np.random.randn(2,1)生成符合标准正态分布的2x1向量，模拟初始"随机站在山上的位置"
theta = np.random.randn(2, 1)# 梯度下降核心循环：通过多次迭代逐步逼近最优参数
for iteration in range(n_iterations):# 计算梯度向量（批量梯度下降：使用全部样本计算梯度）# 公式对应：∇MSE(θ) = 2/m * Xᵀ·(Xθ - y)# X_b.dot(theta)：计算所有样本的预测值（100,1）# X_b.dot(theta) - y：计算所有样本的预测误差（100,1）# X_b.T.dot(...)：通过矩阵转置和乘法，汇总所有样本对梯度的贡献（2,1）# 乘以2/m：根据MSE公式的导数结果，对梯度进行缩放gradients = 2 / m * X_b.T.dot(X_b.dot(theta) - y)# 沿梯度反方向更新参数（梯度是上升最快的方向，反方向是下降最快的方向）# 更新公式：θ_new = θ_old - 学习率×梯度theta = theta - eta * gradients# 输出收敛后的最优参数θ
# 结果应接近真实值[4, 3]（因噪声存在会有小幅偏差）
print("梯度下降收敛后的参数θ（θ₀和θ₁）：")
print(theta)

初始随机的 $\theta$ ：是你随机站在 “山谷周围的山坡上” 的某个位置（不是山顶，山顶是 “成本最大” 的点，初始$\theta$是随机的，可能在任意山坡位置）。
最终输出的 $\theta$ ：是你沿着 “最陡的下坡方向”（梯度反方向），一步步走到的 “山谷底部”—— 也就是 “成本函数最小的位置”，对应线性回归里 “预测误差最小的最优参数”。

这个结果其实和标准方程求出的最优解是相同的，也就是两者的结果相同。
两者的区别如下：
标准方程只适合小数据、简单线性问题（比如几十列特征、几万条数据），数据一大或模型一复杂（比如神经网络），计算就会 “崩掉”（内存不够、算得巨慢）。
梯度下降能处理大数据、复杂模型（比如图像、文本的 AI 模型），但需要 “学习率” 控制 “每一步迈多大步”—— 步长合适才能又快又准找到最优解，步长不对要么慢死，要么 “跑偏”。

3.4 随机梯度下降

随机梯度下降（Stochastic Gradient Descent，SGD）是梯度下降的一种变种，核心特点是每次仅用 “1 个随机样本” 计算梯度并更新参数

1. 与 “批量梯度下降” 的核心区别

批量梯度下降：每次用全部训练样本计算梯度，再更新参数（精准但数据量大时极慢）。
随机梯度下降：每次从训练集中随机选 1 个样本，仅用这个样本计算梯度，立即更新参数（快但梯度有 “随机噪声”）。

2. 关键特点

速度快：只需处理 1 个样本，计算量小，能快速迭代（适合百万级、亿级大数据，或在线学习场景）。
路径震荡但整体下降：由于样本随机性，参数更新路径是上下震荡的，但整体趋势会向成本最小值靠近。
逃离局部最优：若成本函数 “非凸”（存在多个局部最小值），SGD 的随机震荡能 “跳出局部陷阱”，更易找到全局最小值（批量梯度下降易陷在局部里）。

3. 缺陷与改进

SGD 的问题是永远不会精准停在全局最小值（持续震荡），且固定学习率时，后期仍会大幅震荡，无法收敛到最优附近。

解决方法是 **“学习率衰减”（模拟退火思想）**：

前期学习率大：快速探索、逃离局部最优；
后期学习率小：慢慢收敛到全局最小值附近。

# 导入NumPy库，用于数组和矩阵的高效运算（随机梯度下降依赖向量化操作加速计算）
import numpy as npX = 2 * np.random.rand(100, 1)
y = 4 + 3 * X + np.random.randn(100, 1)
X_b = np.c_[np.ones((100, 1)), X]# 定义训练的轮数（epoch）：整个数据集会被遍历50次
n_epochs = 50
# 学习率调度的超参数：控制学习率衰减的节奏（t0为分子基数，t1为分母偏移量）
t0, t1 = 5, 50
# 样本数量：共100个训练样本
m = 100# 学习率调度函数（模拟退火思想）：随着迭代次数t增加，学习率逐渐减小
# 前期学习率大（快速探索参数空间），后期学习率小（精细收敛到最优）
def learning_schedule(t):return t0 / (t + t1)# 随机初始化模型参数θ（包含偏置θ₀和权重θ₁），形状为(2, 1)，初始值服从标准正态分布
# 相当于“随机站在参数空间的某一位置”
theta = np.random.randn(2, 1)# 外层循环：遍历整个数据集的轮次（共n_epochs轮）
for epoch in range(n_epochs):# 内层循环：对每个样本进行一次随机梯度下降更新for i in range(m):# 随机选择一个样本的索引（模拟“随机抽取”单个样本）random_index = np.random.randint(m)# 提取该随机样本的特征向量（xi形状为(1, 2)，保持二维数组格式以适配矩阵运算）xi = X_b[random_index : random_index + 1]# 提取该随机样本的真实标签（yi形状为(1, 1)）yi = y[random_index : random_index + 1]# 计算当前样本的梯度（基于单个样本的均方误差（MSE）导数）# 公式推导：MSE对θ的偏导数，仅用当前单个样本计算（这是“随机”的核心）gradients = 2 * xi.T.dot(xi.dot(theta) - yi)# 计算当前迭代步骤的学习率（t = epoch*m + i 表示全局迭代次数，学习率随迭代次数增大而衰减）eta = learning_schedule(epoch * m + i)# 沿梯度反方向更新参数：θ_new = θ_old - 学习率 × 梯度# 梯度是“上升最快的方向”，反方向是“成本下降最快的方向”theta = theta - eta * gradients# 输出训练完成后收敛的参数θ
# 理论上应接近真实参数[[4], [3]]（因噪声存在，结果会有小幅偏差）
print(theta)

使用Scikit-Learn等效代码

# 导入NumPy库，用于高效的数组和矩阵运算（梯度下降依赖矩阵乘法实现向量化计算）
import numpy as np
from sklearn.linear_model import SGDRegressorX = 2 * np.random.rand(100, 1)
y = 4 + 3 * X + np.random.randn(100, 1)
X_b = np.c_[np.ones((100, 1)), X]# 初始化随机梯度下降回归器（SGDRegressor）
# max_iter=50：最大迭代轮数（遍历数据集的次数），控制训练总步数
# penalty=None：不使用正则化（正则化用于防止过拟合，此处简化模型）
# eta0=0.1：初始学习率（控制参数更新的步长，SGDRegressor默认会自动调整学习率）
sgd_reg = SGDRegressor(max_iter=50, penalty=None, eta0=0.1)# 训练模型：fit方法接收特征X和目标值y
# y.ravel()：将二维数组y转换为一维数组（SGDRegressor要求目标值为一维格式）
# 模型会自动处理偏置项（无需手动传入X_b），内部通过随机梯度下降优化参数
sgd_reg.fit(X, y.ravel())# 输出模型的截距（偏置项θ₀）：对应线性回归中的常数项
# 理论上应接近真实值4（因噪声存在会有偏差）
print("模型截距（θ₀）：", sgd_reg.intercept_)# 输出模型的系数（特征权重θ₁）：对应特征X的斜率
# 理论上应接近真实值3（因噪声和随机梯度的随机性会有偏差）
print("模型系数（θ₁）：", sgd_reg.coef_)

四、多项式回归

多项式回归是一种通过构建 “特征的多项式组合” 来拟合非线性数据的回归模型。它的本质是：将 “非线性问题转化为线性问题求解”（关键！避免误解为 “非线性模型”）。

4.1 生成非线性带噪声数据集

import numpy as np
from matplotlib import pyplot as plt
m = 100
X = 6*np.random.rand(m, 1) -3
y = 0.5*X**2+X+2+np.random.randn(m, 1)
plt.scatter(X, y)
plt.show()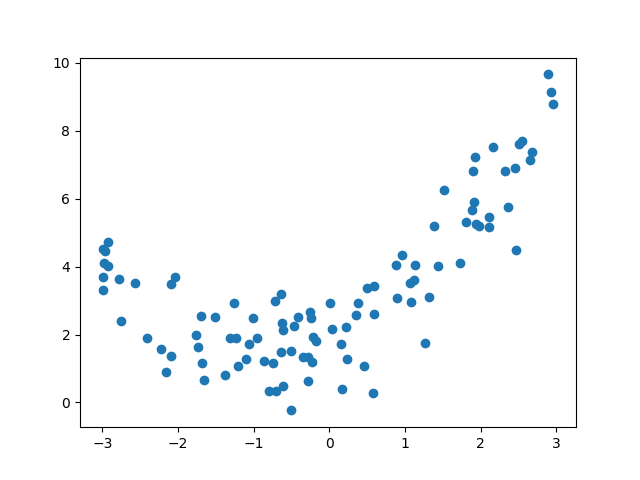

为什么用 np.random.rand() 生成 X？

目的是让 X 在 [-3, 3) 这个区间内 “均匀分布”。

可以拆解一下：

np.random.rand(m, 1) 生成的是 [0,1) 之间的均匀随机数（每个数出现的概率相等）；
乘以 6 后，变成 [0,6) 之间的均匀数；
再减 3，最终变成 [-3, 3) 之间的均匀数。

为什么要让 X “均匀分布”？
因为我们想让 X 在一个区间内 “铺满”，而不是集中在某一小段。比如：

如果 X 都挤在 - 3 附近，那生成的 y 也只会集中在某个小范围，后续模型很难学到整个二次曲线的趋势；
均匀分布能让 X 在 [-3,3) 之间每个位置都有样本，这样生成的 y 能完整体现 “二次函数的曲线形状”（比如抛物线的上升、下降趋势），方便后续模型拟合。

为啥不用randn生成X?

np.random.randn()生成的是正态分布（钟形分布） 的数据，它的特点是：

大部分数据集中在 “均值附近”（比如均值为 0 时，多数数据在 - 1 到 1 之间）；
离均值越远，数据越稀疏（比如大于 3 或小于 - 3 的值极少出现）。

如果用randn()生成 X，会出现什么问题？
假设我们直接用X = np.random.randn(m, 1)，X 的分布会是：

大多数点挤在 0 附近（-1 到 1 之间）；
只有极少数点会出现在 - 3 到 - 1 或 1 到 3 的范围内（甚至可能没有）。

这会导致 y（基于 X 的二次函数）的样本分布也会 “中间密集、两端稀疏”，画出来的散点图会是：

0 附近的点密密麻麻，几乎重叠；
-3 或 3 附近的点可能只有一两个，甚至没有。

这样的数据集有个严重问题：二次函数的 “曲线趋势”（比如抛物线的上升、下降、顶点）无法被完整展示。比如二次函数在 X=-3 和 X=3 时的 y 值差异很大，但如果这两个位置没有足够的样本，后续用多项式回归拟合时，模型很难 “学” 到完整的抛物线形状，可能只会拟合中间密集的部分，导致演示效果失效。

而np.random.rand()生成的是均匀分布的数据，经过6*... -3处理后，X 会在[-3, 3)区间内 “均匀铺开”—— 每个位置的样本数量差不多，-3 附近、0 附近、3 附近都有足够的点。

为什么用randn()（正态分布）生成噪声？

因为真实世界的 “随机误差” 几乎都符合正态分布的特点：

误差平均为 0：不会总是偏大或偏小（比如测量身高时，多测 1cm 和少测 1cm 的概率差不多）；
小误差常见，大误差罕见：大多数误差很小（比如 99% 的误差在 ±3 以内），极少数情况会出现大误差（比如偶尔读数错了，误差 10 以上）。

这和randn()的特性完全匹配：它生成的随机数均值为 0，标准差为 1，大部分值落在 [-3,3] 之间，越靠近 0 出现的概率越高。

4.2 将原始特征转换为多项式特征

import numpy as np
from matplotlib import pyplot as plt
from sklearn.preprocessing import PolynomialFeatures
m = 100
# 形状为(100,1)：100 个样本，每个样本 1 个特征（一元特征）。
# np.random.rand(m, 1)：生成m=100行、1 列的数组，值在[0,1)区间均匀分布；
X = 6*np.random.rand(m, 1) -3
#噪声：+ np.random.randn(m, 1) 加入了正态分布的随机误差（均值 0，标准差 1），让数据更贴近真实场景（不会完美落在曲线上）；
y = 0.5*X**2+X+2+np.random.randn(m, 1)
plt.scatter(X, y)
plt.show()#PolynomialFeatures是 scikit-learn 中用于生成多项式特征的工具；
#degree=2：指定生成二次多项式特征（最高次项为 2 次）；
#include_bias=False：不添加偏置项（即不生成全为 1 的列，后续线性回归会自己加偏置）。
poly_features= PolynomialFeatures(degree=2,include_bias=False)#fit_transform：先 “学习” X 的结构，再将 X 转换为多项式特征；
#转换逻辑（对一元特征X）：
#原始特征x → 转换为[x, x²]（因degree=2）。
X_ploy = poly_features.fit_transform(X)
print(X[0])  # 打印原始特征X的第一个样本
print(X_ploy[0])  # 打印转换后多项式特征X_poly的第一个样本

poly_features = PolynomialFeatures(degree=2, include_bias=False)

这段代码创建了一个PolynomialFeatures类的实例，用于将原始特征转换为多项式特征，是实现多项式回归的核心工具之一。

PolynomialFeatures是 scikit-learn 库中用于特征升维的工具，它能将原始特征（如x）转换为多项式组合特征（如x, x², x³...或x1, x2, x1², x2², x1x2...）。

“将原始特征转换为多项式组合特征” 的核心意思是：基于原始特征，生成新的特征，这些新特征是原始特征的 “多项式形式” 或 “多项式组合形式”。简单说，就是把原始的简单特征（比如单个数值x），变成由它的多次方（比如x²、x³）或与其他特征的乘积（比如x1*x2）组成的 “组合特征”。
例 1：原始特征是一元特征（只有x）
原始特征：x（比如x=3）
当degree=2（二次多项式）时，转换后的 “多项式组合特征” 是：[x, x²]（即[3, 9]）
当degree=3（三次多项式）时，转换后的特征是：[x, x², x³]（即[3, 9, 27]）
例 2：原始特征是多元特征（比如有x1和x2两个特征）
原始特征：[x1, x2]（比如x1=2，x2=3）
当degree=2时，转换后的 “多项式组合特征” 会包含：
所有 1 次项：x1、x2（即2、3）
所有 2 次项：x1²、x2²（即4、9）
所有交叉项（不同特征的乘积）：x1*x2（即2*3=6）
最终组合起来就是：[x1, x2, x1², x2², x1*x2] → [2, 3, 4, 9, 6]

为什么要做这种 “组合”？

假设我们有一个简单的非线性关系：y = 0.5 $x^{^{2}}$ + x + 2（就是代码中 y 的理论值）。

它的图像是一条抛物线（非线性）：

当 x=-3 时，y=0.5×9 + (-3) + 2 = 4.5 - 3 + 2 = 3.5；
当 x=-2 时，y=0.5×4 + (-2) + 2 = 2 - 2 + 2 = 2；
当 x=0 时，y=0 + 0 + 2 = 2；
当 x=2 时，y=0.5×4 + 2 + 2 = 2 + 2 + 2 = 6

如果我们直接用线性模型去拟合这个关系，会怎么样？线性模型只能画一条直线，但抛物线是弯曲的，直线无论如何调整角度，都不可能完美贴合抛物线 —— 这就是 “线性模型无法拟合非线性关系” 的直观表现。

多项式特征组合：把 “非线性关系” 伪装成 “线性关系”

X_ploy = poly_features.fit_transform(X)

X_ploy = poly_features.fit_transform(X) 这行代码是对原始特征 X 进行多项式特征转换的核心操作，它结合了 “学习数据特征” 和 “执行转换” 两个步骤。

4.3 多项式回归模型预测

# 导入必要的库
import numpy as np  # 用于数值计算（生成数据、矩阵运算等）
from matplotlib import pyplot as plt  # 用于数据可视化（绘制散点图、曲线等）
from sklearn.preprocessing import PolynomialFeatures  # 用于生成多项式特征
from sklearn.linear_model import LinearRegression  # 用于构建线性回归模型# 1. 生成模拟数据（用于演示多项式回归）
m = 100  # 样本数量：100个数据点
# 生成特征X：形状为(100, 1)，表示100个样本，每个样本1个特征
# np.random.rand(m, 1)生成[0,1)区间的随机数，乘以6后范围变为[0,6)，再减3最终范围为[-3, 3)
X = 6 * np.random.rand(m, 1) - 3  # 生成目标变量y：基于二次函数关系，并添加噪声
# 真实函数关系为：y = 0.5x² + x + 2（二次曲线）
# 加入噪声项np.random.randn(m, 1)：符合标准正态分布（均值0，标准差1）的随机误差
# 噪声让数据更接近真实场景（不会完美落在理论曲线上）
y = 0.5 * X**2 + X + 2 + np.random.randn(m, 1)# 2. 生成多项式特征（核心步骤：将线性特征转换为多项式特征）
# 创建多项式特征生成器：
# degree=2：指定生成二次多项式特征（最高次项为x²）
# include_bias=False：不添加偏置项（即不生成全为1的列，后续线性回归会自动学习偏置）
poly_features = PolynomialFeatures(degree=2, include_bias=False)# 对原始特征X进行转换：将一维特征[x]转换为二维多项式特征[x, x²]
# fit_transform：先根据X的分布"学习"转换规则，再应用转换
X_poly = poly_features.fit_transform(X)  
# 例如：若原始X的某个样本为x=2，则转换后为[2, 2²]=[2, 4]# 3. 训练多项式回归模型（本质是用线性回归拟合多项式特征）
# 初始化线性回归模型（多项式回归的核心是用线性模型拟合高次项特征）
lin_reg = LinearRegression()
# 用转换后的多项式特征X_poly和目标变量y训练模型
# 模型会学习参数：w1（x的系数）、w2（x²的系数）和w0（偏置项）
lin_reg.fit(X_poly, y)# 4. 提取模型学习到的参数（用于分析或手动计算预测值）
# lin_reg.coef_：模型学到的特征权重，形状为(1, 2)（二维数组）
# 因为X_poly是[x, x²]，所以coef_分别对应w1（x的系数）和w2（x²的系数）
# flatten()：将二维数组转为一维数组，方便解包赋值
w1, w2 = lin_reg.coef_.flatten()  # lin_reg.intercept_：模型学到的偏置项（w0），对应二次函数中的常数项
w0 = lin_reg.intercept_  # 5. 可视化：绘制原始数据和拟合曲线
# 对原始特征X排序：因为原始X是随机生成的（无序），直接绘图会导致曲线混乱
# np.sort(X, axis=0)：按列排序（axis=0），得到从小到大的X值
X_sorted = np.sort(X, axis=0)  # 对排序后的X生成多项式特征（保持与训练时的特征转换规则一致）
# 注意：这里用transform而非fit_transform，避免重新学习规则（确保和训练时一致）
X_sorted_poly = poly_features.transform(X_sorted)  # 用训练好的模型预测排序后X对应的y值（得到拟合曲线的y坐标）
y_pred = lin_reg.predict(X_sorted_poly)  # 绘制拟合曲线和原始数据
plt.plot(X_sorted, y_pred, 'b-', linewidth=3)  # 蓝色实线：多项式回归拟合曲线（排序后X确保曲线平滑）
plt.scatter(X, y, alpha=0.6)  # 散点图：原始数据点（alpha=0.6增加透明度，避免点重叠时看不清）
plt.xlabel('X')  # x轴标签
plt.ylabel('y')  # y轴标签
plt.show()  # 显示图像