量化交易 - Simple Regression 简单线性回归(机器学习)
目录
一、准备
二、导入包
三、构建数据
四、拟合
五、模型效果说明
六、手动公式计算验证
七、作图展示
一、准备
先安装一些库
# ! pip install matplotlib
# ! pip install statsmodels
二、导入包
import warnings
warnings.filterwarnings('ignore')
%matplotlib inlineimport numpy as np
import pandas as pdimport matplotlib.pyplot as plt
import seaborn as snsimport statsmodels.api as sm
from sklearn.linear_model import SGDRegressor
from sklearn.preprocessing import StandardScalersns.set_style('whitegrid')
pd.options.display.float_format = '{:,.2f}'.format三、构建数据
x = np.linspace(-5, 50, 100)
y = 50 + 2 * x + np.random.normal(0, 20, size=len(x))
data = pd.DataFrame({'X': x, 'Y': y})
ax = data.plot.scatter(x='X', y='Y', figsize=(14, 6))
sns.despine()
plt.tight_layout()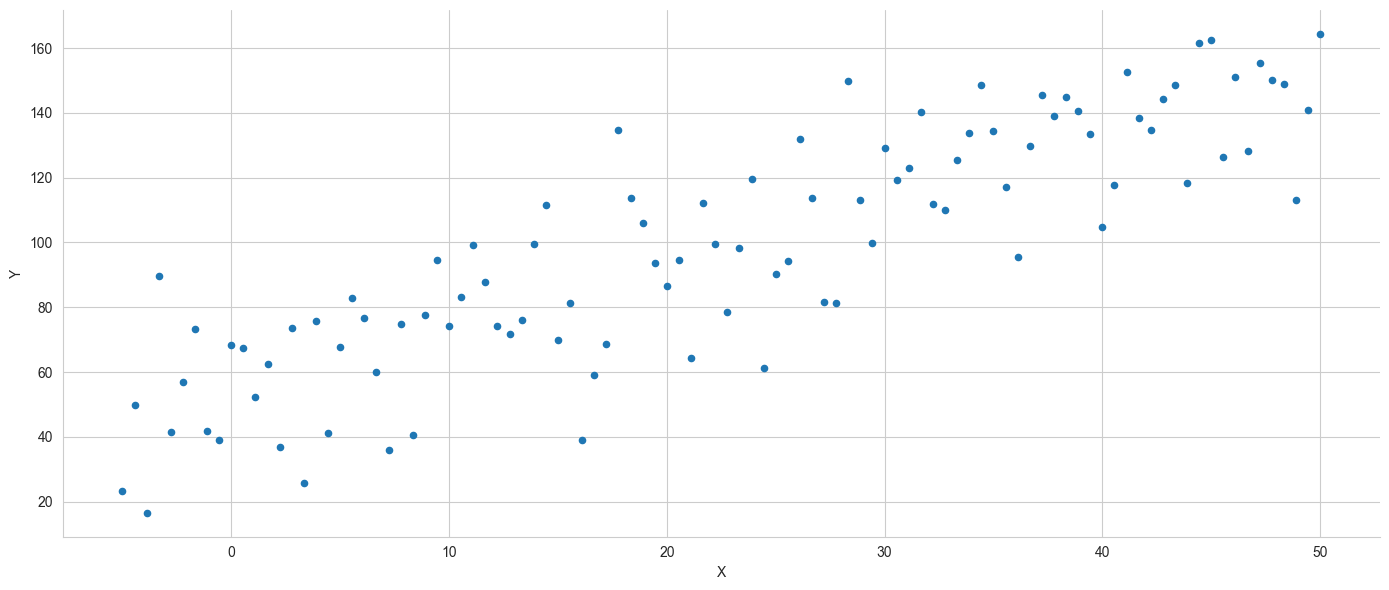
四、拟合
# OLS: Ordinary Least Squares
X = sm.add_constant(data['X'])
model = sm.OLS(data['Y'], X).fit()
print(model.summary())打印模型结果:
OLS Regression Results
==============================================================================
Dep. Variable: Y R-squared: 0.742
Model: OLS Adj. R-squared: 0.739
Method: Least Squares F-statistic: 281.8
Date: Wed, 17 Sep 2025 Prob (F-statistic): 1.39e-30
Time: 16:28:00 Log-Likelihood: -435.02
No. Observations: 100 AIC: 874.0
Df Residuals: 98 BIC: 879.2
Df Model: 1
Covariance Type: nonrobust
==============================================================================coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
const 53.8536 3.263 16.503 0.000 47.378 60.330
X 1.9826 0.118 16.786 0.000 1.748 2.217
==============================================================================
Omnibus: 0.934 Durbin-Watson: 2.030
Prob(Omnibus): 0.627 Jarque-Bera (JB): 1.024
Skew: -0.213 Prob(JB): 0.599
Kurtosis: 2.746 Cond. No. 47.6
==============================================================================Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.五、模型效果说明
R-squared (coefficient of determination)
0.8: The fitting is very good
0.5~0.8: Medium
< 0.5: Poor fitting
Adj-R ² is almost equal to R ² → no overfitting
Prob (F-statistic) < 0.05, good
A p-value less than 0.05 indicates statistical significance
六、手动公式计算验证
# β̂ = (XᵀX)⁻¹Xᵀy
# Calculate by hand using the OLS formula
beta = np.linalg.inv(X.T.dot(X)).dot(X.T.dot(y))
pd.Series(beta, index=X.columns)const 53.85
X 1.98
dtype: float64
可以发现,和模型计算出来的差不多。(详细可见我的视频讲解)
七、作图展示
data['y-hat'] = model.predict()
data['residuals'] = model.resid
ax = data.plot.scatter(x='X', y='Y', c='darkgrey', figsize=(14,6))
data.plot.line(x='X', y='y-hat', ax=ax);
# for _, row in data.iterrows():
# plt.plot((row.X, row.X), (row.Y, row['y-hat']), 'k-')
sns.despine()
plt.tight_layout()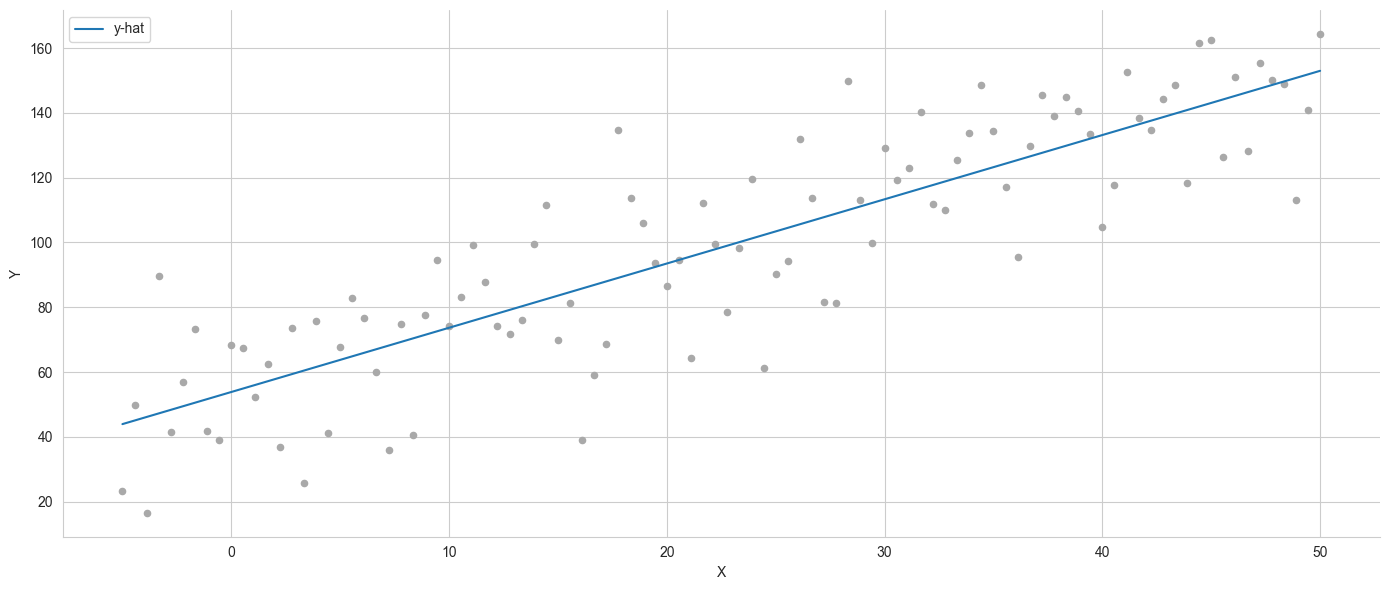
可以发现,基本上是和数据拟合一致的。
# Reference: https://github.com/stefan-jansen/machine-learning-for-trading/blob/main/07_linear_models/01_linear_regression_intro.ipynb
