当前位置：首页 > news >正文

深度学习-线性回归与 Softmax 回归

news 2025/9/18 11:50:18

一、线性回归：用 “数学公式” 预测生活中的连续值

1. 从 “买房出价” 看懂线性回归的核心

看中一套房子，想根据它的户型、面积、地段等信息，估算一个合理的出价，这其实就是线性回归要解决的问题 ——预测一个连续变化的数值。

比如，我们收集了过去的房价数据：

输入（特征）：房子的 “面积（㎡）”“卧室数量”“距离市中心距离（km）”；
输出（标签）：对应的 “成交价格（万元）”。

线性回归的核心，就是找到一个 “线性公式”，把这些特征与房价关联起来。用数学公式表示就是：
y = w₁x₁ + w₂x₂ + w₃x₃ + b
其中：

y 是预测的房价（目标值）；
x₁、x₂、x₃ 是房子的面积、卧室数量、距离等特征；
w₁、w₂、w₃ 是 “权重”，表示每个特征对房价的影响程度（比如面积的权重更大，说明面积对房价影响更显著）；
b 是 “偏置”，相当于一个基础偏移量。

如果用矩阵简化表达，就是更简洁的 y = Xw + b（X 是特征矩阵，w 是权重向量）。这个公式看似简单，却是很多复杂预测任务的 “基石”—— 小到预测气温、股票涨跌，大到工业生产中的质量预测，都能看到它的影子。

2. 线性回归的 “神经网络视角”

从结构上看，它可以看作是最简单的单层神经网络：

输入层：对应房子的特征（面积、卧室数等），每个特征是一个 “神经元”；
输出层：对应预测的房价，只有一个 “神经元”；
权重与偏置：输入层到输出层的连接边就是权重 w，输出层神经元自带偏置 b，没有隐藏层（这就是 “单层” 的含义）。

这种极简结构，让线性回归成为理解神经网络的 “敲门砖”—— 后续复杂的深度学习模型，本质上0就是在这样的基础上增加层数、丰富连接方式。

3. 让模型 “学会” 预测：损失函数与梯度下降

线性回归的核心目标，是让预测值 y 与真实房价尽可能接近。如何衡量 “接近程度”就需要损失函数（衡量模型预测误差的 “标尺”）。

（1）损失函数：给模型的 “预测打分”

最常用的是平方损失（L₂损失），公式为：
L = ½∑(y_true - y_pred)²
其中 y_true 是真实房价，y_pred 是模型预测的房价。损失值越小，说明模型预测得越准。

比如，一套房子真实价格是 200 万元，模型预测 205 万元，平方损失就是 ½×(200-205)²=12.5；如果预测 198 万元，损失就是 ½×(200-198)²=2，显然后者更优。

（2）梯度下降：让模型 “沿着正确方向优化”

有了损失函数，下一步就是找到 “让损失最小化” 的权重 w 和偏置 b。

这就需要深度学习中最基础的优化算法 ——梯度下降。它的核心逻辑很像 “盲人下山”：

梯度（由所有参数的偏导数组成的向量）就像 “指南针”，指示着 “损失下降最快的方向”（严格来说，是梯度的反方向）；
模型从随机初始化的 w 和 b 开始（相当于盲人在山上随机位置），沿着梯度反方向 “迈一步”（更新参数），每一步的 “步长” 就是学习率；
重复这个过程，直到损失不再明显下降，此时的 w 和 b 就是 “最优参数”。

举个直观的例子：如果损失函数是 “f (x₀,x₁)=x₀²+x₁²”（类似一个 “碗状” 曲面），梯度会指向曲面的最低点，离最低点越远，梯度向量越长（步长越大），离得越近，梯度向量越短（步长越小），最终会精准收敛到最小值。

（3）优化细节：学习率与批量大小的 “平衡术”

梯度下降的效果，很大程度上取决于两个超参数：

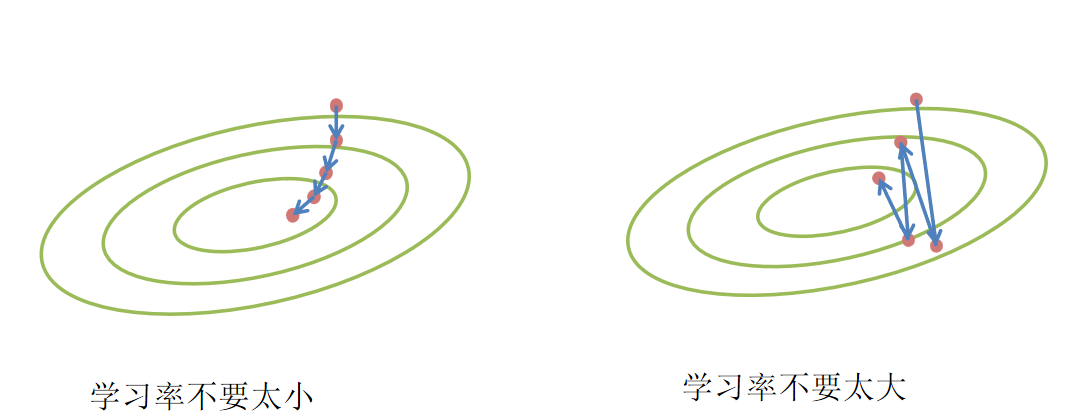
学习率：步长不能太大（否则会 “越过” 最低点，在山上反复横跳），也不能太小（否则下山太慢，训练效率极低），通常需要通过实验调整（比如 0.01、0.001）；
批量大小：实际训练时，我们不会用全部数据计算梯度（“全量梯度下降”），而是随机选一小批数据（“小批量随机梯度下降”）。批量太小，难以利用硬件并行计算资源；批量太大，会浪费资源且更新不及时，一般选择 32、64、128 等常用值。

如今，小批量随机梯度下降已经成为深度学习的 “默认优化算法”，从简单的线性回归到复杂的 GPT 模型，都离不开它的身影。

二、Softmax 回归：从 “预测数值” 到 “分类类别” 的跨越

1. 回归与分类的 “核心区别”

线性回归解决 “预测连续值”（如房价、气温），但现实中还有大量 “分类” 问题 —— 比如：

识别一张图片是 “猫” 还是 “狗”（二分类）；

判断一封邮件是否为 “垃圾邮件”（二分类）；

识别手写数字是 0-9 中的哪一个（多分类）；

给维基百科评论贴 “有毒 / 侮辱 / 威胁” 等标签（多标签分类）。

这些问题的核心是预测离散的 “类别”，而非连续的数值。此时，线性回归就不够用了 —— 比如用线性回归预测手写数字，输出可能是 “5.2”“3.8”，但我们需要的是 “明确属于哪一类” 的结果。这就需要 Softmax 回归登场。

2. Softmax 回归：给每个类别 “分配概率”

Softmax 回归是专门为多类分类设计的模型，它在 linear 层（线性计算）的基础上，增加了一个 “Softmax 运算”，核心作用是：将线性输出转换为 “概率分布”，让每个类别的预测结果更具解释性。

（1）从 “线性输出” 到 “概率分布” 的转换

假设我们要解决 “手写数字识别”（10 类分类，输出 0-9）：

首先，通过线性层计算每个类别的 “原始得分”（logits）：o₀, o₁, ..., o₉（对应 0-9 每个数字的原始输出，可能是任意实数，比如 [1, -1, 2, 0.5, ...]）；
然后，对这些原始得分做 Softmax 运算：
yᵢ = exp(oᵢ) / ∑(exp(oₖ))（k 从 0 到 9）。

这个运算有两个关键作用：

用 exp (oᵢ) 确保输出值 “非负”（概率不能为负）；
除以所有 exp (oₖ) 的总和，确保所有类别的概率之和为 1（符合概率分布的定义）。

举个例子：如果原始得分是 [1, -1, 2]，Softmax 运算后结果为：

exp(1)≈2.718，exp(-1)≈0.368，exp(2)≈7.389；
总和≈2.718+0.368+7.389≈10.475；
最终概率≈[0.26, 0.04, 0.7]。

这意味着：模型预测该样本属于 “第 2 类” 的概率是 70%，属于 “第 0 类” 的概率是 26%，属于 “第 1 类” 的概率是 4%—— 我们直接取概率最大的类别作为最终预测结果即可。

（2）Softmax 回归的 “网络结构”

和线性回归类似，Softmax 回归也是一种单层神经网络，但输出层神经元数量等于 “类别数”：

输入层：手写数字图像的像素特征（比如 28×28 的图像展开为 784 个特征）；
输出层：10 个神经元，对应 0-9 每个数字的概率（通过 Softmax 运算得到）；
全连接：输入层每个神经元都与输出层所有神经元连接，因此也叫 “全连接层”。

这种结构虽然简单，却能解决很多经典分类问题：比如 MNIST 手写数字识别（10 类）、ImageNet 图像分类（1000 类）的基础模型，甚至 Kaggle 上的 “蛋白质图像分类”（28 类）、“恶语评论分类”（7 类），都能基于它扩展实现。

3. 分类任务的 “损失函数”：交叉熵损失

分类任务不能再用线性回归的 “平方损失” 了 —— 因为平方损失会让模型更新效率低，且对类别概率的 “惩罚不够精准”。此时，交叉熵损失成为更优选择。

交叉熵损失的核心思想是：衡量模型预测的概率分布与真实标签的 “差距”，公式为：
H(p, q) = -∑(pᵢ log(qᵢ))
其中：

p 是 “真实标签的概率分布”（比如样本真实是 “5”，则 p 为 [0,0,0,0,0,1,0,0,0,0]，只有第 5 类概率为 1）；
q 是 “模型预测的概率分布”（比如 [0.02,0.01,0.03,0.01,0.02,0.85,0.02,0.02,0.01,0.01]）。

交叉熵损失值越小，说明模型预测的概率分布与真实标签越接近。比如，上面例子中，交叉熵损失会重点惩罚 “第 5 类概率不够大” 的问题，让模型快速向 “正确类别” 收敛。

三、两大回归模型的核心对比：一张表看懂区别与联系

对比维度	线性回归	Softmax 回归
核心任务	预测连续值（如房价、气温）	预测离散类别（如数字、图像类别）
输出层结构	1 个神经元	类别数 = 神经元数
关键运算	线性计算（y=Xw+b）	线性计算 + Softmax 运算
损失函数	平方损失（L₂损失）	交叉熵损失
典型应用	房价预测、销量预测	手写数字识别、垃圾邮件分类
本质关系	Softmax 回归是线性回归在分类任务的扩展	共享 “线性计算 + 梯度下降” 的核心逻辑

四、回归模型的 “进阶思考”：从基础到深度学习

线性回归和 Softmax 回归看似简单，却是深度学习的 “敲门砖”。理解它们，你会发现复杂模型的底层逻辑其实很统一：

模型结构：都是 “输入层→线性计算→输出层” 的基础框架，复杂模型只是增加了 “隐藏层” 和 “非线性激活函数”；
优化逻辑：都依赖 “梯度下降” 寻找最优参数，区别仅在于损失函数和输出层运算；
应用扩展：线性回归可扩展为 “多项式回归”（解决非线性问题），Softmax 回归可与 CNN 结合（解决图像分类）、与 RNN 结合（解决文本分类）。

比如，在自动驾驶中，线性回归可以预测车辆的 “刹车距离”（连续值），Softmax 回归可以判断 “前方物体是行人、车辆还是交通灯”（分类）—— 两者结合，就能完成更复杂的感知任务。