彩笔运维勇闯机器学习--梯度下降法

前言

彩笔运维勇闯机器学习，今天我们来讨论一下梯度下降法

梯度

首先要搞明白什么是梯度，那就要先从导数说起

导数

函数$y=f(x)$的自变量$x$在一点$x_0$上产生一个增量$\Delta x$时，函数输出值的增量$\Delta y=f(x_0+\Delta x)-f(x_0)$与自变量增量$\Delta x$的比值在$\Delta x$趋于0时的极限$a$如果存在，$a$即为在$x_0$处的导数

$$f^{\prime }(x)=\frac{\partial y}{\partial x}=\underset{\Delta x\to 0}{\lim }\frac{f(x+\Delta x)-f(x)}{\Delta x}=a$$

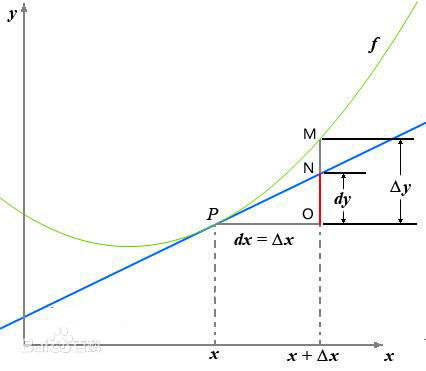
（该图来自于百度百科）

偏导数

偏导数与导数的本质是一样的，只不过偏导数解决的是多变量的问题

$$\frac{\partial f}{\partial x_i}=\underset{\Delta x_i\to 0}{\lim }\frac{f(x_1,\dots ,x_i+\Delta x_i,\dots ,x_n)-f(x_1,\dots ,x_i,\dots ,x_n)}{\Delta x_i}$$

比如二元函数$f(x,y)$

对$x$求偏导：
$$\frac{\partial f}{\partial x}=\underset{\Delta x\to 0}{\lim }\frac{f(x+\Delta x,y)-f(x,y)}{\Delta x}$$

对$y$求偏导：

$$\frac{\partial f}{\partial y}=\underset{\Delta y\to 0}{\lim }\frac{f(x,y+\Delta y)-f(x,y)}{\Delta y}$$

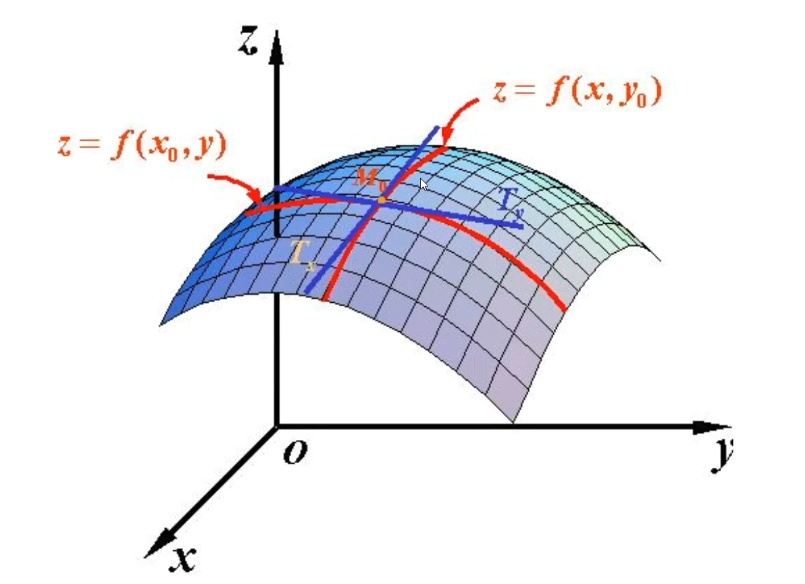
（该图来自于百度百科）

超过二元的就画不出来图来了

方向导数

导数与偏导数都是自变量相对于某一轴方向（比如x相对于x轴，y相对于y轴）讨论变化率，而方向导数讨论的则是，自变量可以在其定义域内自由选择方向

一个多元函数$f$和一个方向向量$u$，方向导数$D_{u}f$表示函数$f$在$u$方向的变化率

$$D_{\mathbf{u}}f(a)=\underset{h\to 0}{\lim }\frac{f(a+hu)-f(a)}{h}$$

用二元函数举例：

$$D_{\mathbf{u}}f(x_0,y_0)=\underset{h\to 0}{\lim }\frac{f(x_0+h{u}_1,y_0+h{u}_2)-f(x_0,y_0)}{h}$$

• $u_1{u}_2$表示方向$u=(u1,u2)$
• h表示沿着$u$方向的位移

梯度

梯度是多元函数在某一点处所有偏导数构成的向量，表示函数在该点处变化最快的方向及其变化率，对于$f(x_1,x_2,...,x_n)$，其梯度记为$\nabla f$

$$\nabla f=\left(\frac{\partial f}{\partial x_1},\frac{\partial f}{\partial x_2},\dots ,\frac{\partial f}{\partial x_n}\right)$$

• 方向：梯度指向函数在该点增长最快的方向
• 大小：梯度的模表示函数在该方向上的最大变化率

方向导数：梯度与单位方向向量u的点积

$$D_{u}f=\nabla f\cdot u$$

当$u$与$\nabla f$同方向时，方向导数最大
当$u$与$\nabla f$反方向时，方向导数最小

小结

梯度与方向导数：梯度是方向导数中变化率最大的那一个：梯度的方向是方向导数取最大值的方向，而梯度的模长（大小）等于该最大方向导数的值
方向导数与偏导数：偏导数是方向导数的特例，即$u=(0,1)$，简而言之，方向导数在坐标轴上移动，就是偏导数

了解了梯度的诞生以及概念之后，终于可以来讨论一下本文的主题：梯度下降法

梯度下降法

在回归任务中，用于评估模型的重要指标是损失函数MSE，提高模型的泛化能力就是设法降低MSE

上述关于梯度的描述，梯度就是函数变化率最快的方向，那梯度下降法就是不断沿着付梯度方向寻找MSE的最小值。不同于最小二乘法只能用于线性模型，梯度下降法适用于大部分模型，包括线性回归、逻辑回归等等

核心思想

• 函数的梯度指向函数值增长最快的方向，负梯度方向则是函数值下降最快的方向
• 通过不断沿负梯度方向调整参数，逐步逼近函数的最小值点

步骤

• 初始化，随机选择初始参数或者全部设置为0
• 迭代更新，每迭代一次都会更新参数的值：$${\theta }_{t+1}={\theta }_t-\eta \cdot \nabla f({\theta }_t)$$
  • ${\theta }_t$：第$t$次迭代的参数值
  • $\eta$：每次更新的幅度，也叫学习率
  • $\nabla J({\theta }_t)$：目标函数$f$在${\theta }_t$的梯度
• 终止迭代的条件：
  • 梯度很小：梯度的模长很小，一般小于$10^{-6}$
  • 损失函数变化很小：一般小于$10^{-6}$
  • 到达最大迭代次数

计算过程

我们用本系列的第一节：一元线性回归中的数据，用梯度下降法详细演示一次

data = {'result': [0.63, 0.72, 0.72, 0.63, 0.57, 0.52, 0.48, 0.47],'feature1': [22.48, 19.50, 18.02, 16.97, 15.78, 15.11, 14.02, 13.24]
}

目标是找到一组参数，使得损失函数MSE最小：
$$\text{MSE}=\frac{1}{n}\sum _{i=1}^n(y_i-{\hat{y}}_i{)}^2$$

带入$y={\beta }_0+{\beta }_{1}x$
$$f({\beta }_0,{\beta }_1)=\frac{1}{n}\sum _{i=1}^n({\beta }_0+{\beta }_1{x}_i-{\hat{y}}_i{)}^2$$

首先计算梯度，分别对${\beta }_0$、${\beta }_1$求偏导

先对${\beta }_0$求偏导：

$$\frac{\partial f}{\partial {\beta }_0}=\frac{1}{n}\sum _{i=1}^{n}2({\beta }_0+{\beta }_1{x}_i-{\hat{y}}_i)\cdot ({\beta }_0+{\beta }_1{x}_i-{\hat{y}}_i{)}^{\prime }=\frac{2}{n}\sum _{i=1}^n({\beta }_0+{\beta }_1{x}_i-{\hat{y}}_i)$$

在对${\beta }_1$求偏导：

$$\frac{\partial f}{\partial {\beta }_1}=\frac{1}{n}\sum _{i=1}^{n}2({\beta }_0+{\beta }_1{x}_i-{\hat{y}}_i)\cdot ({\beta }_0+{\beta }_1{x}_i-{\hat{y}}_i{)}^{\prime }=\frac{2}{n}\sum _{i=1}^n({\beta }_0+{\beta }_1{x}_i-{\hat{y}}_i)\cdot x_i$$

至此得出梯度：
$$\nabla f=(\frac{2}{n}\sum _{i=1}^n({\beta }_0+{\beta }_1{x}_i-{\hat{y}}_i),\frac{2}{n}\sum _{i=1}^n({\beta }_0+{\beta }_1{x}_i-{\hat{y}}_i)\cdot x_i)$$

设置参数，学习率$\eta =0.001$，迭代次数100次，开始迭代：

1）第一轮迭代，先初始化${\beta }_0$ ${\beta }_1$为0

计算损失函数：
$$\begin{array}{rl}MSE& =f({\beta }_0,{\beta }_1)=\frac{1}{n}\sum _{i=1}^n({\beta }_0+{\beta }_1{x}_i-{\hat{y}}_i{)}^2\\ & =\frac{1}{8}[(0-0.63{)}^2+(0-0.72{)}^2+...+(0-0.47{)}^2]=0.35965\end{array}$$

计算梯度：

$$\begin{array}{rl}\frac{\partial f}{\partial {\beta }_0}& =\frac{2}{n}\sum _{i=1}^n({\beta }_0+{\beta }_1{x}_i-{\hat{y}}_i)\\ & =\frac{1}{4}[(0-0.63)+(0-0.72)+...+(0-0.47)]=-1.185\end{array}$$

$$\begin{array}{rl}\frac{\partial f}{\partial {\beta }_1}& =\frac{2}{n}\sum _{i=1}^n({\beta }_0+{\beta }_1{x}_i-{\hat{y}}_i)\cdot x_i\\ & =\frac{1}{4}[(0-0.63)\cdot 22.48+(0-0.72)\cdot 19.50+...+(0-0.47)\cdot 13.24]=-20.418025\end{array}$$

$$\nabla f=(-1.185,-20.418025)$$

损失函数与梯度均小于$10^{-6}$，继续迭代第二轮

2）第二轮迭代，先初始化${\beta }_0$ ${\beta }_1$

$${\beta }_0\leftarrow {\beta }_0-\eta \cdot \frac{\partial f}{\partial {\beta }_0}=0-0.001\cdot (-1.185)=0.001185$$

$${\beta }_1\leftarrow {\beta }_1-\eta \cdot \frac{\partial f}{\partial {\beta }_1}=0-0.001\cdot (-20.418025)=0.020418025$$

计算损失函数：

$$MSE=f({\beta }_0,{\beta }_1)=\frac{1}{n}\sum _{i=1}^n({\beta }_0+{\beta }_1{x}_i-{\hat{y}}_i{)}^2=0.064501$$

计算梯度：

$$\frac{\partial f}{\partial {\beta }_0}=\frac{2}{n}\sum _{i=1}^n({\beta }_0+{\beta }_1{x}_i-{\hat{y}}_i)=-0.492909$$

$$\frac{\partial f}{\partial {\beta }_1}=\frac{2}{n}\sum _{i=1}^n({\beta }_0+{\beta }_1{x}_i-{\hat{y}}_i)\cdot x_i=-8.395268$$

$$\nabla f=(-0.492909,-8.395268)$$

损失函数与梯度均小于$10^{-6}$，继续迭代第三轮…

就这样不断迭代下去，直至满足停止的条件，停止之后，该轮次的${\beta }_0$ ${\beta }_1$就是最佳参数

联系我

• 联系我，做深入的交流

---

至此，本文结束
在下才疏学浅，有撒汤漏水的，请各位不吝赐教…