【脑电分析系列】第15篇:脑电功能连接性与脑网络分析(二):Granger因果性、图论指标与复杂网络构建
摘要:
欢迎回到脑电分析系列!在前几篇中,我们探讨了时域(ERP)、频域(PSD)以及时频(ERSP)分析。上一篇我们深入了解了脑功能连接的基础,包括相干性(Coherence)、相位锁定值(PLV)和互信息(Mutual Information),它们主要描述脑区间的统计依赖关系。
本篇将聚焦于更高阶的连接性分析——有效连接(Effective Connectivity),特别是其核心方法Granger因果性(Granger Causality)。此外,我们将深入探讨如何使用图论指标(如度、路径长度、聚类系数和模块化)来量化脑网络的拓扑结构,并通过Python代码,利用MNE和NetworkX库,展示如何从EEG数据构建和分析复杂脑网络。本文旨在帮助你从“相关性”走向“因果性”,从“连接”走向“网络”,更深入地理解大脑区域间的动态互动。
关键词:
脑电分析, EEG, 脑功能连接, 有效连接, Granger因果性, 图论, 复杂网络, Python, MNE, NetworkX
引言:从“相关”到“因果”的飞跃
大脑是一个由无数神经元和脑区构成的复杂网络。为了理解其如何协同工作,我们不仅需要知道哪些区域活动是同步的(功能连接),更需要探究一个区域的活动是否能预测或驱动另一个区域的活动(有效连接)。
功能连接(如相干性)告诉我们A和B是“一起活动”的,但无法回答是谁在影响谁。有效连接则致力于回答这个问题,它为我们揭示大脑信息流动的方向性,这对于理解认知任务中的信息处理路径,以及诊断神经系统疾病(如癫痫发作的起源、阿尔茨海默病中信息传递的障碍)至关重要。
比较表:有效连接 vs. 功能连接
| 类型 | 定义 | 示例指标 | 典型应用场景 |
| 功能连接 | 脑区间的统计依赖(如同步) | 相干性、PLV | 无方向性任务分析、静息态 |
| 有效连接 | 脑区间的因果影响(如预测) | Granger因果、动态因果模型(DCM) | 方向性网络研究、任务态 |
一、 有效连接与Granger因果性
1.1 Granger因果性的基本概念
Granger因果性(Granger Causality, GC)是一种基于统计学而非物理学的因果推断方法。其核心思想是:如果信号A的过去值能够显著提高对信号B未来值的预测精度,那么我们就可以说A是B的Granger原因。这里的“因果”并非绝对的物理因果关系,而是一种基于时间序列预测的统计因果关系。
在EEG分析中,GC可以用来评估一个电极(或脑区)的活动是否能够预测另一个电极(或脑区)的活动,从而推断出信息流动的方向。
1.2 Granger因果性的计算
GC的计算通常基于向量自回归(Vector Autoregressive, VAR)模型。
时域计算:
GC的计算通过比较两种自回归模型的残差方差来完成。
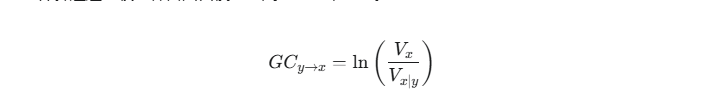
其中,Vx是单独使用信号x的过去值预测其未来值的模型残差方差;$V_{x|y}$是同时使用信号$x$和y的过去值预测信号x未来值的模型残差方差。如果$V_{x|y}$显著小于$V_x$,说明信号y的过去值提供了额外的信息,对预测信号x未来值有帮助,则$GC_{y \to x}$大于0。
频域计算:
为了探究特定频率的信息流,GC也可以在频域中计算。
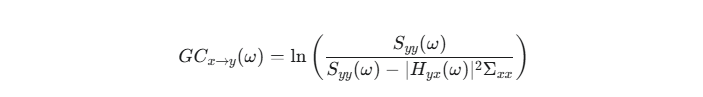
其中,S是功率谱,H是谱转移矩阵,Σ是噪声协方差。频域GC可以揭示不同脑电节律(如Alpha波或Beta波)在信息传递中的作用。
Python示例1:使用MNE计算Granger因果
MNE-Connectivity库提供了强大的功能来计算Granger因果性。以下代码展示了如何对样本MEG数据(可以类比EEG)进行Granger因果分析。
Python
import mne
import numpy as np
from mne.datasets.fieldtrip_cmc import data_path
from mne_connectivity import spectral_connectivity_epochs# 加载MEG数据(模拟EEG),并进行预处理
raw = mne.io.read_raw_ctf(data_path() / "SubjectCMC.ds")
raw.pick("mag")
raw.crop(50.0, 110.0).load_data()
raw.notch_filter(50)
raw.resample(100)
epochs = mne.make_fixed_length_epochs(raw, duration=2.0).load_data()# 定义传感器组,模拟两个脑区(A:顶叶,B:枕叶)
signals_a = [idx for idx, ch_info in enumerate(epochs.info["chs"]) if ch_info["ch_name"][2] == "P"]
signals_b = [idx for idx, ch_info in enumerate(epochs.info["chs"]) if ch_info["ch_name"][2] == "O"]
indices_ab = (np.array([signals_a]), np.array([signals_b]))# 计算Granger因果
gc_ab = spectral_connectivity_epochs(epochs,method=["gc"],indices=indices_ab,fmin=5,fmax=30,rank=(np.array([5]), np.array([5])),gc_n_lags=20, # 自回归模型阶数
)# 输出结果形状 (连接数, 频率数)
print(gc_ab.get_data().shape)
Python示例2:Granger因果可视化
Python
from matplotlib import pyplot as pltfreqs = gc_ab.freqs
fig, axis = plt.subplots(1, 1)
axis.plot(freqs, gc_ab.get_data()[0], linewidth=2)
axis.set_xlabel("频率 (Hz)")
axis.set_ylabel("Granger因果值 (A.U.)")
fig.suptitle("GC: 顶叶 => 枕叶")
plt.show()
二、 图论指标:量化脑网络的拓扑结构
在得到连接矩阵(如Granger因果矩阵)后,我们可以使用图论(Graph Theory)来量化和描述脑网络的拓扑结构。这有助于识别网络的“枢纽”节点、信息传递效率以及社区结构。
2.1 核心图论指标
度(Degree):节点的连接数。在加权图中,它代表与节点相连的边的权重总和。
意义:度值高的节点(枢纽节点)在网络中扮演着重要的整合角色,能够有效地与许多其他节点交流。
路径长度(Path Length):衡量信息在网络中传递的效率。
特征路径长度(Characteristic Path Length):所有节点对之间最短路径的平均值。
意义:路径长度越短,网络的信息传递效率越高。
聚类系数(Clustering Coefficient):衡量网络中的局部聚类程度,即一个节点的邻居之间互相连接的紧密程度。
意义:高聚类系数反映了网络的分离特性,即节点倾向于形成紧密的局部簇或社区。
模块化(Modularity):衡量网络划分成模块(或社区)的强度。
意义:高模块化值表示网络内部存在明显的子结构,这些子结构内的连接比子结构间的连接更密集。在脑网络中,这反映了不同功能模块(如视觉、听觉、运动模块)的存在。
2.2 Python示例:使用NetworkX计算图论指标
NetworkX是一个强大的Python库,用于创建、操作和研究复杂网络的结构、动态和功能。
Python
import networkx as nx
import numpy as np# 假设 conn_matrix 是一个 (n_nodes x n_nodes) 的连接矩阵
# 这里我们用一个随机矩阵作为示例
n_nodes = 30
conn_matrix = np.random.rand(n_nodes, n_nodes)
np.fill_diagonal(conn_matrix, 0) # 自身连接为0# 构建有向图(对于Granger因果)
G = nx.from_numpy_array(conn_matrix, create_using=nx.DiGraph)# 1. 计算度
degrees = dict(G.degree(weight='weight'))
print("节点的加权度:", degrees)# 2. 计算特征路径长度
# 注意:对于有向图,如果不是强连通,计算可能会失败,可以先转换为无向图
G_undirected = G.to_undirected()
if nx.is_connected(G_undirected):avg_path_length = nx.average_shortest_path_length(G_undirected, weight='weight')print(f"平均路径长度: {avg_path_length:.4f}")# 3. 计算聚类系数
avg_clustering = nx.average_clustering(G_undirected, weight='weight')
print(f"平均聚类系数: {avg_clustering:.4f}")# 4. 计算模块化 (需要安装'python-louvain'库: pip install python-louvain)
import community as community_louvainpartition = community_louvain.best_partition(G_undirected)
modularity = community_louvain.modularity(partition, G_undirected, weight='weight')
print(f"模块化: {modularity:.4f}")
三、 复杂网络构建与分析的完整流程
从EEG数据到复杂的脑网络分析,通常遵循以下步骤:
数据预处理:对EEG数据进行滤波、伪影去除、分段和基线校正。
节点定义:通常将每个EEG通道定义为一个网络节点。在更高级的分析中,也可以使用源定位(Source Localization)将皮层区域作为节点。
边定义:根据研究目的,选择合适的连接指标(如Granger因果性、相干性、PLV等)计算节点间的连接强度,得到一个连接矩阵。
阈值化与图构建:对连接矩阵应用阈值(如绝对阈值或稀疏度阈值),去除弱连接,构建成一个加权或二值的图(Graph)。对于Granger因果性,通常构建有向图。
图论分析:使用NetworkX等库计算图论指标,量化网络拓扑结构。
统计与解释:比较不同任务或不同群体(如健康组与患者组)的图论指标,以揭示脑网络结构的差异及其与认知或疾病的关联。
结论:从单一信号到复杂网络的全景图
本篇博客将脑电分析从单一信号的时频分析,拓展到了多通道间的复杂互动。通过:
Granger因果性,我们能够从统计预测的角度揭示脑区间信息流动的方向性,为理解大脑的因果机制提供了可能。
图论指标,我们得以用量化的方式描述脑网络的拓扑结构,识别其效率、聚类特性和功能模块。
将两者结合,我们可以构建出反映大脑动态互动的复杂网络模型,这对于揭示认知任务中的信息流重组、诊断神经疾病的连接异常,以及开发基于特定连接模式的脑机接口都具有深远的意义。在实践中,需要严格的预处理和对结果的谨慎解读。
