当前位置：首页 > news >正文

【CF】Day144——杂题 (交互 + 思维 | 整除分块)

news 2025/9/18 6:44:36

D. Tournament Countdown

题目：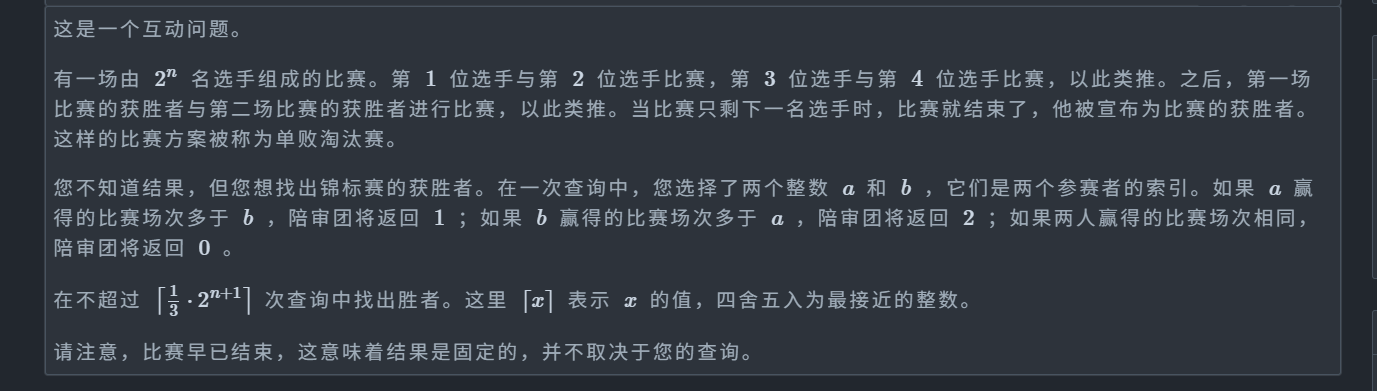

思路：

很有意思的一题

注意到题目中的限制，操作次数居然乘了个 1 / 3，这其实是一种启发，在启示我们可以使用更少的操作删除更多的无用条件

如果没操作次数限制，那么显然我们可以直接一个一个问，然后取最大的即可，但是现在要求变严格了，现在我们必须要在两次操作中删除三个数

那么如何操作呢？

我们查看相邻的四个元素，如下图

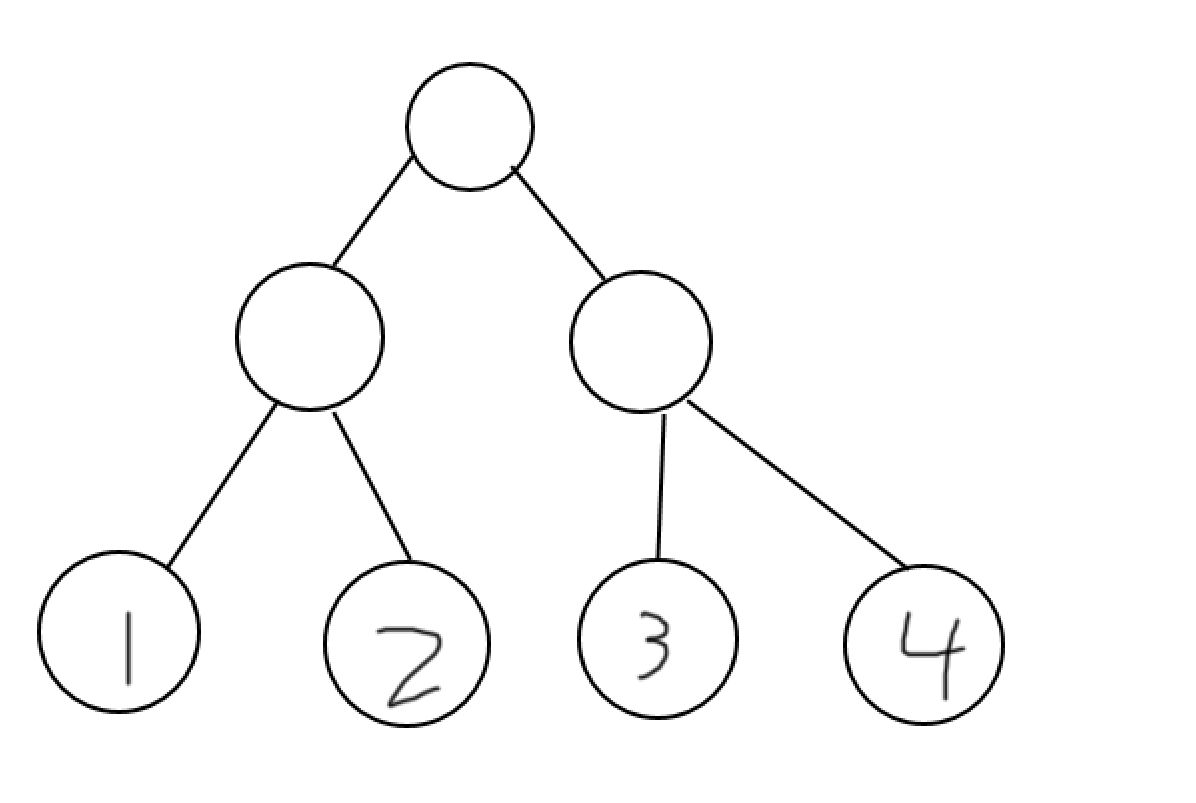
我们查询 1 3，那么就有三种情况

①.1 = 3

此时 1 和 3 都不能跑到第一层，同时也不可能跑的第二层，因为跑到第一层一定是赢的最多的，而跑到第二层一定是二者还要再度比较的，所以 1 和 3 只在第三层一开始就结束了，因此 1 3 就能直接删除，然后比较 2 4 即可

②.1 > 3

既然 1 > 3，说明 1 一定赢了 2，那么此时 2 3 就都没用了，所以直接比较 1 4 即可

③.1 < 3

同②.，此时直接比较 2 3 即可

至此我们就使用了两次操作删除了 3 个数，那么这样一直删 3 个数，最后要不就是一个数，要不就是两个数，两个数时特判一下即可（剩余数是显然的，对 3 取模的原理）

具体实现看代码

代码：

#include <bits/stdc++.h>
using namespace std;
#define int long long
#define yes cout << "YES\n"
#define no cout << "NO\n"
mt19937 rnd(chrono::steady_clock::now().time_since_epoch().count());int qp(int a, int b)
{int res = 1;while (b){if (b & 1)res = res * a;a = a * a;b >>= 1;}return res;
}
int x;int ask(vector<int>& k)
{cout << "? " << k[0] << " " << k[2] << endl;cin >> x;if(x == 1){cout << "? " << k[0] << " " << k[3] << endl;cin >> x;if(x == 1) return k[0];else return k[3];}else if(x == 2){cout << "? " << k[1] << " " << k[2] << endl;cin >> x;if(x == 1) return k[1];else return k[2];}else{cout << "? " << k[1] << " " << k[3] << endl;cin >> x;if(x == 1) return k[1];else return k[3];}
}void solve()
{int n;cin >> n;int mx = qp(2,n);vector<int> a(mx),b;iota(a.begin(),a.end(),1);auto geta = [&]()->int{int num = a.back();a.pop_back();return num;};while (a.size() > 2){while (!a.empty()){vector<int> k;for(int i = 0;i < 4;i++) k.push_back(geta());b.push_back(ask(k));}a = b;b.clear();}if(a.size() == 2){cout << "? " << a[0] << " " << a[1] << endl;cin >> x;if(x == 2) a[0] = a[1];}cout << "! " << a[0] << endl;
}signed main()
{int t = 1;cin >> t;while (t--){solve();}return 0;
}

D. Price Tags

题目：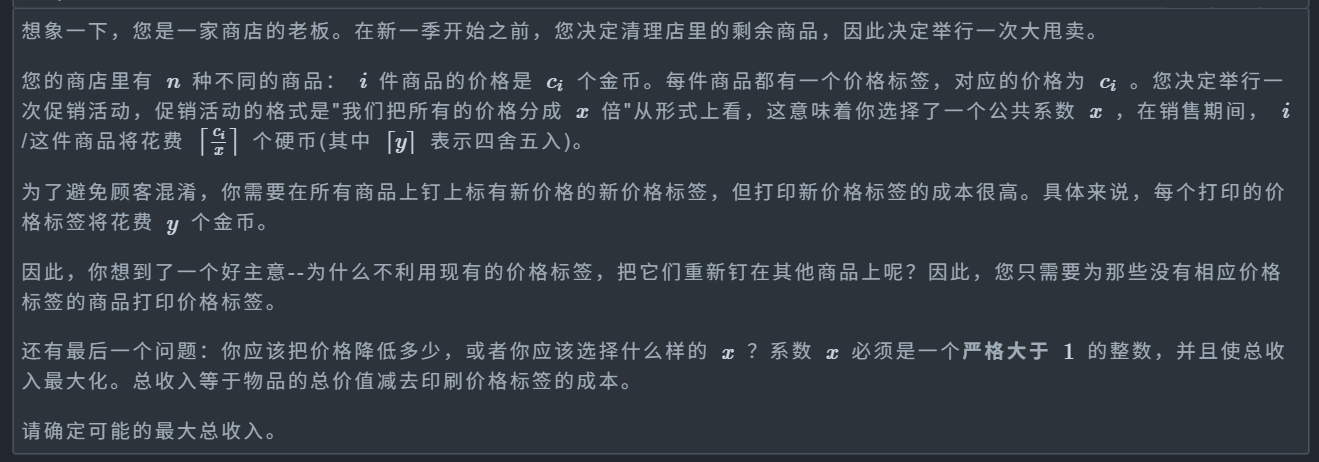

思路：

以后看到求整体除以 x 的操作应该立马想到整除分块，当然还要注意数据

题目很简单，要求我们找出一个 x，使得收入最大，并给出具体最大总收入

首先本题既不能贪心，也不能二分，甚至dp也无从下手，但是注意到题目中的操作： $\sum \left \lceil \frac{c[i]}{x} \right \rceil$ ，以及条件 c[i] <= 2e5

这种操作不就是类似我们的整除分块吗，只不过此处是上去整罢了，但是不影响我们的同样思路，同时个体数据很小，感觉可行

所以我们可以暴力枚举 x，然后继续计算，具体的：我们定义 cnt[i] 为小于 i 的所有正整数的数量，那么对于每一个枚举的 x，我们来进行计算其奉献，我们初始化答案为 -y * n，那么对于 0 ~ j，这一段的所有数除以 x 结果都是 j / x，所以这段的奉献就是 d * j / x（其中 d = cnt[j] - cnt[j - x]），而题目中还有一个贴标签的条件，这也很简单，我们只需要先计算数字 D = j / x 的数量，然后和 d 取一个 min 即可，即代表有多少标签已经有了

具体实现看代码

代码：

#include <bits/stdc++.h>
using namespace std;
#define int long long
#define yes cout << "YES\n"
#define no cout << "NO\n"
mt19937 rnd(chrono::steady_clock::now().time_since_epoch().count());
int N = 3e5;
void solve()
{int n, y;cin >> n >> y;vector<int> a(n), cnt(N+1, 0);for (int i = 0; i < n; i++){cin >> a[i];cnt[a[i]]++;}for (int i = 1; i <= N; i++){cnt[i] += cnt[i - 1];}int ans = LLONG_MIN;for (int x = 2; x <= N; x++){int temp = -y * n;for (int i = x; i <= N; i += x){int d = cnt[i] - cnt[i - x];int D = i / x;temp += d * D;temp += y * min(d,cnt[D] - cnt[D-1]);}ans = max(ans, temp);}cout << ans << endl;
}signed main()
{cin.tie(0)->sync_with_stdio(0);int t = 1;cin >> t;while (t--){solve();}return 0;
}