【Leetcode hot 100】108.将有序数组转换为二叉搜索树

问题链接

108.将有序数组转换为二叉搜索树

问题描述

给你一个整数数组 nums ，其中元素已经按 升序 排列，请你将其转换为一棵 平衡 二叉搜索树。

示例 1：

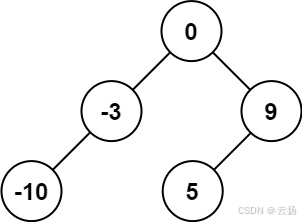
输入：nums = [-10,-3,0,5,9]
输出：[0,-3,9,-10,null,5]
解释：[0,-10,5,null,-3,null,9] 也将被视为正确答案：

示例 2：

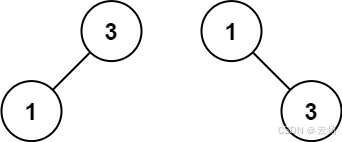
输入：nums = [1,3]
输出：[3,1]
解释：[1,null,3] 和 [3,1] 都是高度平衡二叉搜索树。

提示：

• 1 <= nums.length <= 10^4
• -10^4 <= nums[i] <= 10^4
• nums 按 严格递增 顺序排列

问题解答

本题核心是利用升序数组的特性和平衡二叉搜索树（BST）的定义，通过「分治思想」构建树结构。平衡BST要求左右子树高度差不超过1，而升序数组的中间元素作为根节点时，左右子树的节点数会尽可能均匀，天然满足平衡条件。

题目基础概念

• 平衡BST：任意节点的左右子树高度差的绝对值不超过1。
• 升序数组与BST的关联：BST的中序遍历结果是升序序列，因此升序数组可视为BST的中序遍历结果，只需确定「根节点位置」即可反向构建树。
• 根节点选择：数组长度为奇数时，中间元素唯一；为偶数时，选左中间（left + (right-left)/2）或右中间（(left+right+1)/2）均可，不影响平衡（题目允许答案不唯一）。

递归解法（推荐）

递归是最直观的实现，符合分治思想：将数组划分为「根节点+左子数组+右子数组」，递归构建左、右子树。

1. 递归思路

• 参数定义：传入数组nums、左边界left、右边界right（左闭右闭区间，避免重复创建子数组，提高效率）。
• 终止条件：当left > right时，返回null（空节点）。
• 单层逻辑：
  1. 计算中间索引mid（避免(left+right)/2的整数溢出问题）；
  2. 以nums[mid]为值创建根节点；
  3. 递归构建左子树（区间[left, mid-1]）；
  4. 递归构建右子树（区间[mid+1, right]）；
  5. 返回根节点。

2. 递归代码

// 二叉树节点定义（LeetCode环境中已默认提供，此处为清晰展示）
class TreeNode {int val;TreeNode left;TreeNode right;TreeNode() {}TreeNode(int val) { this.val = val; }TreeNode(int val, TreeNode left, TreeNode right) {this.val = val;this.left = left;this.right = right;}
}class Solution {public TreeNode sortedArrayToBST(int[] nums) {// 初始调用：处理整个数组（左边界0，右边界nums.length-1）return buildTree(nums, 0, nums.length - 1);}// 递归构建子树的核心方法private TreeNode buildTree(int[] nums, int left, int right) {// 终止条件：区间无效，返回空节点if (left > right) {return null;}// 计算中间索引（避免溢出：left + (right-left)/2 等价于 (left+right)/2，但无溢出）int mid = left + (right - left) / 2;// 1. 创建当前根节点（中间元素）TreeNode root = new TreeNode(nums[mid]);// 2. 递归构建左子树（左区间：[left, mid-1]）root.left = buildTree(nums, left, mid - 1);// 3. 递归构建右子树（右区间：[mid+1, right]）root.right = buildTree(nums, mid + 1, right);// 返回当前根节点，供父节点连接return root;}
}

3. 复杂度分析

• 时间复杂度：O(n)，每个节点仅创建1次，共n个节点。
• 空间复杂度：O(log n)，递归栈深度为树的高度（平衡BST的高度为log n）。

迭代解法（模拟递归）

递归的本质是「栈/队列的隐式调用」，迭代法通过队列模拟递归过程，存储「待赋值的节点」和「对应的左右边界」。

1. 迭代思路

• 队列设计：用3个队列分别存储：
  1. nodeQueue：待赋值的节点（初始时创建一个空根节点占位）；
  2. leftQueue：每个节点对应的左边界；
  3. rightQueue：每个节点对应的右边界。
• 循环逻辑：
  1. 出队当前节点、左边界、右边界；
  2. 计算中间索引mid，给当前节点赋值；
  3. 若左区间[left, mid-1]有效，创建左子节点，入队左子节点及对应边界；
  4. 若右区间[mid+1, right]有效，创建右子节点，入队右子节点及对应边界；
  5. 重复至队列为空。

2. 迭代代码

class Solution {public TreeNode sortedArrayToBST(int[] nums) {if (nums.length == 0) {return null;}// 1. 初始化队列：存储节点、左边界、右边界Queue<TreeNode> nodeQueue = new LinkedList<>();Queue<Integer> leftQueue = new LinkedList<>();Queue<Integer> rightQueue = new LinkedList<>();// 2. 根节点占位（初始值无意义，后续赋值），入队整个数组的边界TreeNode root = new TreeNode(0);nodeQueue.offer(root);leftQueue.offer(0);rightQueue.offer(nums.length - 1);// 3. 循环处理每个节点while (!nodeQueue.isEmpty()) {// 出队当前节点和对应的边界TreeNode currNode = nodeQueue.poll();int left = leftQueue.poll();int right = rightQueue.poll();// 计算中间索引，给当前节点赋值int mid = left + (right - left) / 2;currNode.val = nums[mid];// 处理左子树：左区间[left, mid-1]有效时，创建左子节点并入队if (left <= mid - 1) {currNode.left = new TreeNode(0); // 占位nodeQueue.offer(currNode.left);leftQueue.offer(left);rightQueue.offer(mid - 1);}// 处理右子树：右区间[mid+1, right]有效时，创建右子节点并入队if (right >= mid + 1) {currNode.right = new TreeNode(0); // 占位nodeQueue.offer(currNode.right);leftQueue.offer(mid + 1);rightQueue.offer(right);}}return root;}
}

3. 复杂度分析

• 时间复杂度：O(n)，每个节点仅赋值1次，共n个节点。
• 空间复杂度：O(n)，队列最多存储n个节点（最坏情况为满二叉树，底层节点数为n/2）。

关键注意点

1. 避免整数溢出：计算mid时用left + (right - left)/2，而非(left + right)/2（当left和right接近int最大值时，后者会溢出）。
2. 区间定义一致性：全程使用「左闭右闭区间」，避免边界处理混乱（若用左闭右开，需调整终止条件和区间划分）。
3. 平衡的保证：每次选中间元素为根，左右子树的节点数差不超过1，因此树的高度为log n，天然满足平衡条件。

测试案例验证

案例1：输入nums = [-10,-3,0,5,9]

• 中间索引mid = 0 + (4-0)/2 = 2，根节点为0；
• 左子树处理[-10,-3]（mid=0 + (1-0)/2=0，根为-10），右子树处理[5,9]（mid=3 + (4-3)/2=3，根为5）；
• 最终树结构：[0,-10,5,null,-3,null,9]（或其他合法平衡BST）。

案例2：输入nums = [1,3]

• 中间索引mid=0 + (1-0)/2=0，根节点为1，右子树为3（结构[1,null,3]）；
• 若选右中间mid=(0+1+1)/2=1，根节点为3，左子树为1（结构[3,1]），均符合要求。