当前位置：首页 > news >正文

第三章神经网络入门笔记：从概念到实践全解析

news 2025/9/16 14:47:03

一、神经网络核心概念

1.1 什么是人工神经网络？

1.2 神经网络的结构

1.3 深度学习与机器学习的关系

二、关键组件：激活函数

2.1 常见激活函数及特性

（1）Sigmoid 函数

（2）Tanh 函数

（3）ReLU 函数（目前最常用）

（4）SoftMax 函数

2.2 激活函数选择指南

三、参数初始化方法

3.1 常见初始化方式

3.2 PyTorch 实现代码

3.3 初始化选择建议

四、神经网络搭建与参数计算（PyTorch 实战）

4.1 搭建流程

4.2 实战：搭建一个简单神经网络

4.3 模型参数计算规则

五、损失函数：衡量模型预测误差

5.1 分类任务损失函数

（1）多分类交叉熵损失（CrossEntropyLoss）

（2）二分类交叉熵损失（BCELoss）

5.2 回归任务损失函数

（1）MAE（L1 损失）

（2）MSE loss（Mean Squared Loss/ Quadratic Loss也被称为L2 loss，或欧氏距离）它以误差的平方和的均值作为距离

（3）Smooth L1 损失：smooth L1说的是光滑之后的L1

六、网络优化方法

6.1 梯度下降基础概念

6.2 常见梯度下降变体

6.3 进阶优化算法

（1）指数加权平均

（2）Momentum（动量法）

（3）AdaGrad

（4）RMSProp

（5）Adam（目前最常用）

6.4 学习率衰减策略

七、正则化：缓解过拟合

7.1 Dropout（随机失活）

7.2 批量归一化（BN 层）

八、实战案例：手机价格分类

8.1 需求分析

8.2 数据准备

8.3 模型构建

8.4 模型训练

8.5 模型评估

8.6 模型调优建议

九、神经网络的优缺点

十、总结

一、神经网络核心概念

1.1 什么是人工神经网络？

人工神经网络（Artificial Neural Network, ANN），简称神经网络（NN），是模仿生物神经网络结构和功能的计算模型。

生物神经元：由树突（接收信号）、细胞核（处理信号）、轴突（输出信号）组成，当树突接收的信号累积到一定电位时，神经元被激活并通过轴突传递信号。
人工神经元：模拟生物神经元的工作机制，通过 “加权求和 + 激活函数” 实现信号处理，

1.2 神经网络的结构

神经网络由多层神经元连接而成，信息单向传递（前向传播），核心分为三层：

层级	作用	特点
输入层	接收原始数据（如特征向量）	神经元数量 = 输入特征维度
隐藏层	对输入数据进行非线性变换和特征提取	可多层叠加，层数 / 神经元数决定模型复杂度
输出层	输出模型预测结果（分类 / 回归）	神经元数量 = 预测目标维度（如多分类任务的类别数）

全连接神经网络（FCN） 是最基础的网络结构，其特点为：

同一层神经元之间无连接；
第 N 层每个神经元与第 N-1层所有神经元相连；
第 N-1层的输出即为第 N 层的输入；
每个连接对应一个权重 w 和偏置 b。

如下图所示：

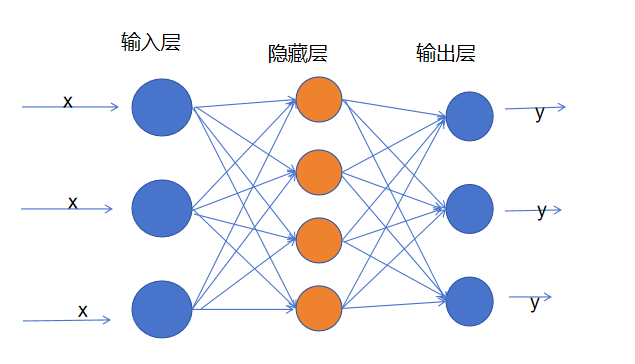
这张图展示了一个全连接神经网络（FCN）的典型结构，由输入层、隐藏层、输出层三层组成，各层神经元通过带权重的连接传递信息。

输入层包含 3 个蓝色神经元，代表模型的原始输入特征。
隐藏层包含 4 个橙色神经元，是对输入数据进行非线性变换和特征提取的核心层。它通过 “加权求和 + 激活函数” 的方式，将输入层的原始特征转化为更抽象的中间特征。这一层的神经元数量（4 个）和层数（图中仅 1 层隐藏层，实际可叠加多层）决定了模型的复杂度。
输出层包含 3 个蓝色神经元，负责输出模型的预测结果。

若为分类任务，神经元数量对应类别数（如多分类的 4 个价格区间）；
若为回归任务，可能仅 1 个神经元输出连续值。

注意：连接与权重层与层之间的蓝色连线代表权重（w），每个连接都有一个专属权重，用于衡量输入对输出的影响程度。训练过程中，这些权重会通过梯度下降不断优化，以最小化预测误差。

因为图片有点草率，推荐一个网站，可以更清晰的表述神经网络之间的结构关系A Neural Network Playgroundhttps://playground.tensorflow.org/#activation=sigmoid&batchSize=10&dataset=circle®Dataset=reg-plane&learningRate=0.03®ularizationRate=0&noise=0&networkShape=4,2&seed=0.75397&showTestData=false&discretize=false&percTrainData=50&x=true&y=true&xTimesY=false&xSquared=false&ySquared=false&cosX=false&sinX=false&cosY=false&sinY=false&collectStats=false&problem=regression&initZero=false&hideText=false

1.3 深度学习与机器学习的关系

深度学习是机器学习的子集，核心区别在于是否依赖 “特征工程”：
- 传统机器学习（如决策树、SVM）：需人工设计特征（如手动提取图像的边缘、纹理）；
- 深度学习：通过神经网络自动从数据中学习特征，无需人工干预。

二、关键组件：激活函数

激活函数的核心作用是为神经网络注入非线性因素，使模型能够拟合复杂的非线性关系。若缺少激活函数，无论网络有多少层，本质都是线性模型（等价于单层线性回归）。

2.1 常见激活函数及特性

（1）Sigmoid 函数

1.公式：

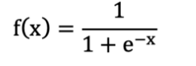
导数：

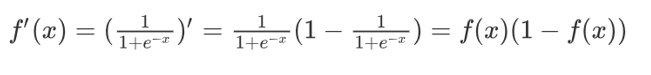
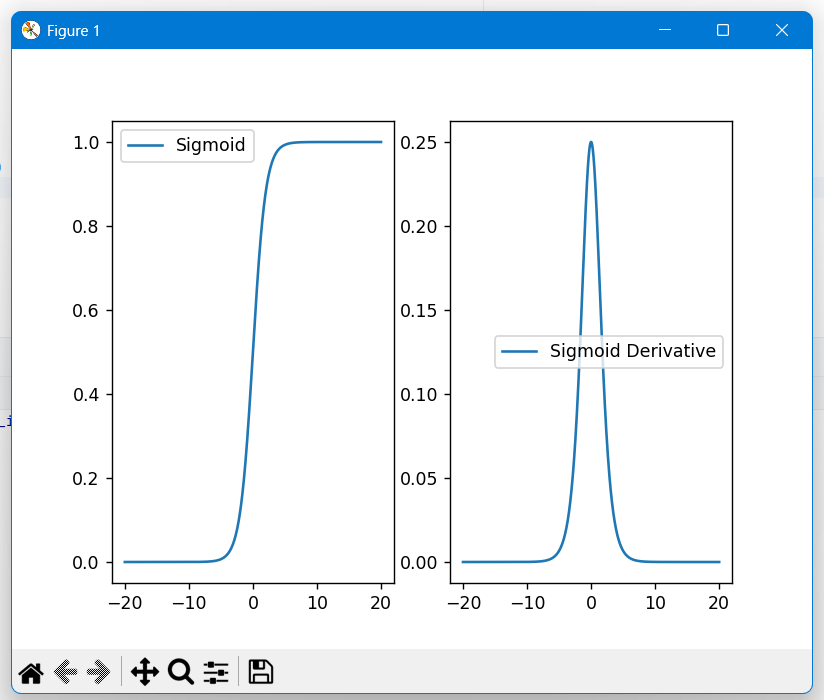
激活函数的图像：

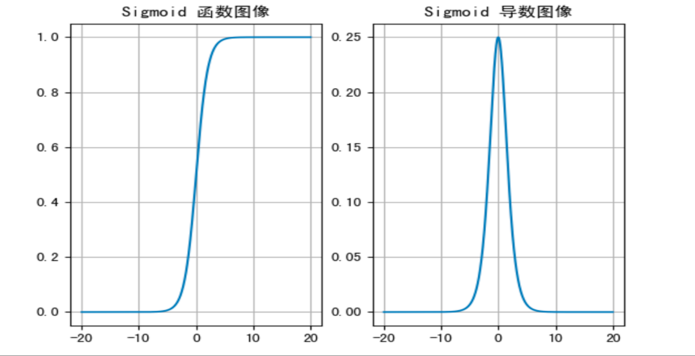
特性：

优点：输出映射到 (0, 1)，可表示概率；

缺点：

当输入的值大致在 <-6 或者 >6 时，意味着输入任何值得到的激活值都是差不多的，这样会丢失部分的信息。
导数范围 (0, 0.25)，易出现 “梯度消失”（倒数下降太快、5 层内明显）；
该激活函数并不是以 0 为中心的，所以在实践中这种激活函数使用的很少。sigmoid函数一般只用于二分类的输出层。

PyTorch 代码实现：

import torch
import matplotlib.pyplot as pltx = torch.linspace(-20, 20, 1000)
y = torch.sigmoid(x)  # Sigmoid函数计算
# 绘制函数与导数图像
_, axes = plt.subplots(1, 2)
axes[0].plot(x, y, label='Sigmoid')
axes[0].legend()
# 计算导数
x.requires_grad = True
torch.sigmoid(x).sum().backward()
axes[1].plot(x.detach(), x.grad, label='Sigmoid Derivative')
axes[1].legend()
plt.show()

输出结果

（2）Tanh 函数

公式：

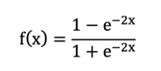
导数：

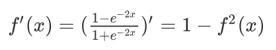
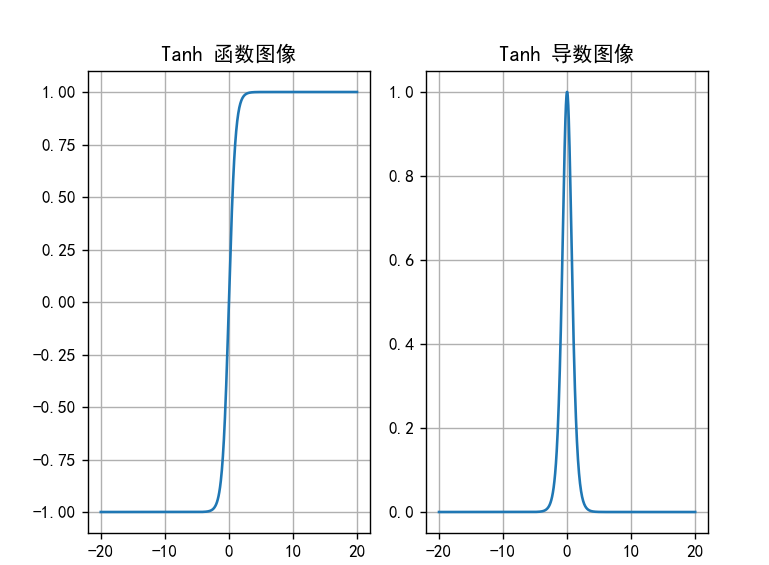
Tanh 函数的函数图像、导数图像如下：

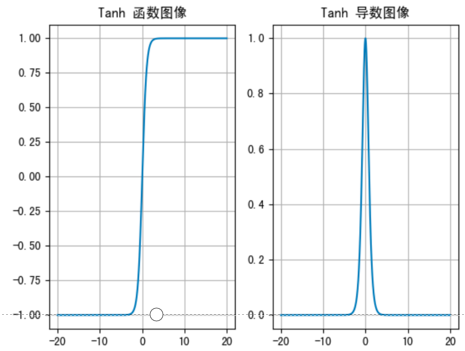
特性：

输出映射到 (-1, 1)，以 0 为中心，收敛速度比 Sigmoid 快；
输入 (|x| > 3) 时，导数趋近于 0，仍存在梯度消失问题；
适合用于隐藏层，输出层可搭配 Sigmoid（二分类）。

pyTorch代码实现：


import torch
import matplotlib.pyplot as pltplt.rcParams['axes.unicode_minus'] = False  # 解决负号'-'显示为方块的问题
plt.rcParams['font.sans-serif'] = ['SimHei']  # 设置字体，正确显示中文# 创建画布和坐标轴
_, axes = plt.subplots(1, 2)
# 函数图像
x = torch.linspace(-20, 20, 1000)
y = torch.tanh(x)
axes[0].plot(x, y)
axes[0].grid()
axes[0].set_title('Tanh 函数图像')
# 导数图像
x = torch.linspace(-20, 20, 1000, requires_grad=True)
torch.tanh(x).sum().backward()
axes[1].plot(x.detach(), x.grad)
axes[1].grid()
axes[1].set_title('Tanh 导数图像')
plt.show()

输出结果：

（3）ReLU 函数（目前最常用）

公式：f(x) = max(0, x)
导数：f'(x) = 1 或 0

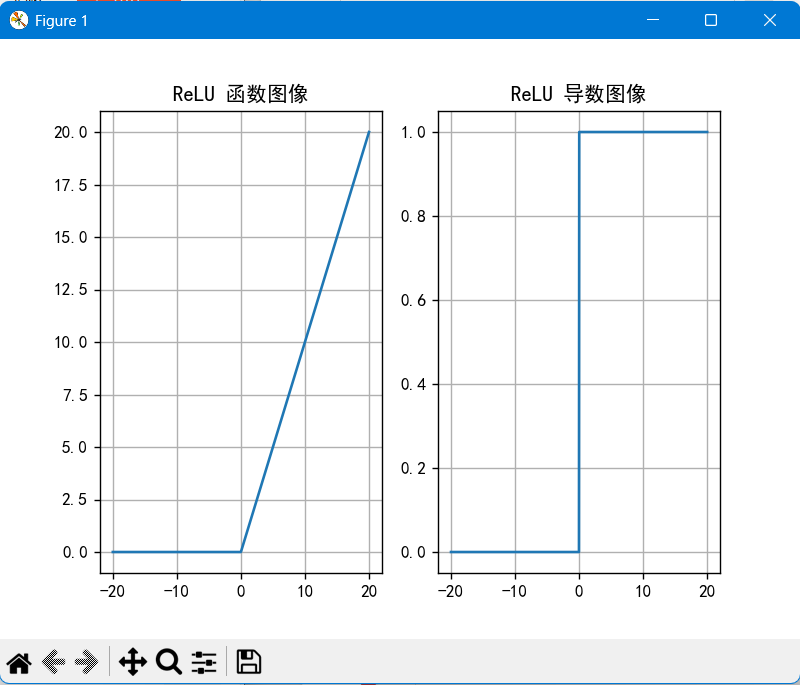
特性：
- 计算简单（无需指数运算），训练效率高；
- x>0 时梯度不衰减，能缓解梯度消失问题；
- 缺点：x < 0 时神经元 “死亡”（权重无法更新）；
- 优势：引入网络稀疏性，减少过拟合风险。

pyTorch代码实现：

# 创建画布和坐标轴
_, axes = plt.subplots(1, 2)
# 函数图像
x = torch.linspace(-20, 20, 1000)
y = torch.relu(x)
axes[0].plot(x, y)
axes[0].grid()
axes[0].set_title('ReLU 函数图像')
# 导数图像
x = torch.linspace(-20, 20, 1000, requires_grad=True)
torch.relu(x).sum().backward()
axes[1].plot(x.detach(), x.grad)
axes[1].grid()
axes[1].set_title('ReLU 导数图像')
plt.show()

输出结果：

（4）SoftMax 函数

公式：

特性：
- 将输出映射为概率分布（所有类别概率和为 1）；
- 专为多分类任务设计，通常用于输出层；
- 对输入差异敏感，易受异常值影响。
PyTorch 实现：

scores = torch.tensor([0.2, 0.02, 0.15, 0.15, 1.3, 0.5, 0.06, 1.1, 0.05, 3.75])
probabilities = torch.softmax(scores, dim=0)  # 按行计算概率
print("类别概率分布:", probabilities)
print("概率和:", probabilities.sum())  # 输出为1.0"""
输出结果：
类别概率分布: tensor([0.0212, 0.0177, 0.0202, 0.0202, 0.0638, 0.0287, 0.0185, 0.0522, 0.0183,0.7392])
概率和: tensor(1.0000)
"""

其他常见的激活函数：

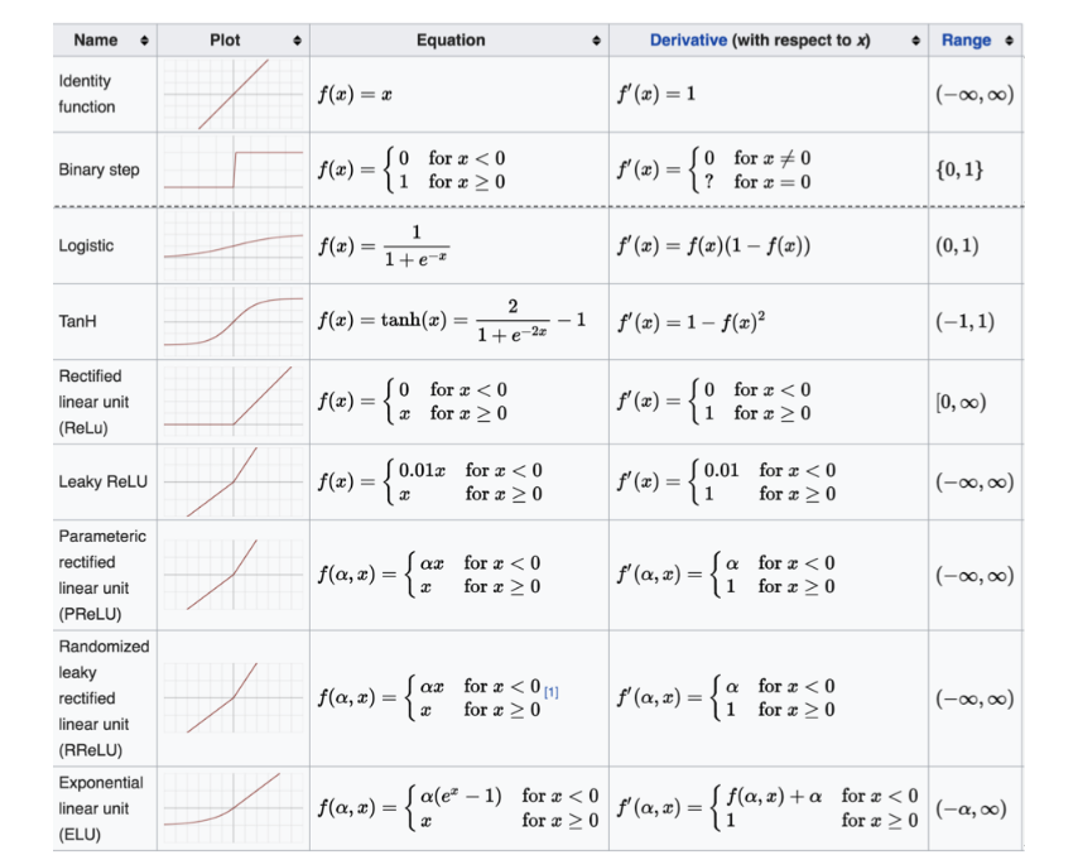
2.2 激活函数选择指南

层级	选择建议
隐藏层	优先使用 ReLU；若出现神经元死亡，尝试 Leaky ReLU、PReLU
输出层	二分类：Sigmoid；多分类：SoftMax；回归：恒等函数（无激活）

三、参数初始化方法

神经网络的参数（权重 w、偏置 b）初始化直接影响模型收敛速度和性能。若初始化不当，可能导致梯度消失 / 爆炸。

3.1 常见初始化方式

初始化方法	原理	适用场景
全 0 / 全 1 初始化	将所有参数设为 0 或 1	不推荐（导致神经元输出一致，无法更新）
均匀分布初始化	权重参数初始化从区间均匀随机取值。即在(-1/√d,1/√d)均匀分布中生成当前神经元的权重，其中d为每个神经元的输入数量	通用场景
正态分布初始化	随机初始化从均值为0，标准差是1的高斯分布中取样，使用一些很小的值对参数W进行初始化	通用场景
Xavier 初始化（也叫做 Glorot初始化）	一种是正态分布的 xavier 初始化、一种是均匀分布的 xavier 初始化正态化的Xavier初始化 stddev = sqrt(2 / (fan_in + fan_out)) 均匀分布的Xavier初始化从[-limit，limit] 中的均匀分布中抽取样本, （limit 是 sqrt(6 / (fan_in + fan_out)) fan_in 是输入神经元的个数， fan_out 是输出的神经元个数）	搭配 Sigmoid/Tanh（输入输出方差平衡）
Kaiming 初始化（也叫做 HE 初始化）	HE 初始化分为正态分布的 HE 初始化、均匀分布的 HE 初始化. 正态化的he初始化 stddev = sqrt(2 / fan_in) 均匀分布的he初始化它从 [-limit，limit] 中的均匀分布中抽取样本, （limit是 sqrt(6 / fan_in) fan_in 输入神经元的个数）	搭配 ReLU（解决 ReLU 导致的方差衰减）

3.2 PyTorch 实现代码

import torch
import torch.nn as nn# 1. 均匀分布初始化
linear = nn.Linear(5, 3)
nn.init.uniform_(linear.weight)  # 从[0,1)均匀采样# 2. 正态分布初始化
nn.init.normal_(linear.weight, mean=0, std=1)# 3. Xavier初始化
nn.init.xavier_normal_(linear.weight)  # 正态分布
# nn.init.xavier_uniform_(linear.weight)  # 均匀分布# 4. Kaiming初始化
nn.init.kaiming_normal_(linear.weight)  # 正态分布
# nn.init.kaiming_uniform_(linear.weight)  # 均匀分布# 5. 固定值初始化
nn.init.constant_(linear.weight, 5)  # 所有权重设为5

3.3 初始化选择建议

PyTorch 各层（如nn.Linear）有默认初始化方法，优先使用Kaiming（搭配 ReLU） 或 Xavier（搭配 Sigmoid/Tanh）；
避免使用全 0 / 全 1 初始化，防止神经元 “同质化”。

四、神经网络搭建与参数计算（PyTorch 实战）

4.1 搭建流程

在pytorch中定义深度神经网络其实就是层堆叠的过程，继承自nn.Module，并重写两个核心方法：

__init__：定义网络层结构（如线性层、激活函数）；
forward：定义前向传播路径（数据在网络中的流动方式）。

4.2 实战：搭建一个简单神经网络

import torch                      # 导入PyTorch库,torch的作用为
from torch import nn              # 导入PyTorch的神经网络模块nn
from torchsummary import summary  # 导入模型结构可视化工具"""
神经网络搭建的具体思路：
第一步：明确网络的 框架，也就是输入层、隐藏层和输出层的结构设计输入层设计：根据输入数据的特征维度确定。隐藏层设计：决定网络的深度和宽度输出层设计：根据任务类型确定输出维度。
第二步：实现网络结构的搭建，1.继承nn.Module类，2.定义网络层和参数初始化3.定义数据的前向传播路径和数据的传输方式
第三步：训练网络，通过反向传播算法更新网络参数，使得网络在训练数据上的性能达到最优。
第四步：测试网络，通过测试数据集评估网络的性能。
第五步：可视化网络结构，通过summary函数打印网络结构和参数信息。
"""
# 定义自定义神经网络类
class Self_Net(nn.Module):  # 继承PyTorch的基础神经网络模块类def __init__(self):# 调用父类的初始化方法，这是必须的步骤super(Self_Net, self).__init__()# 定义网络层结构 nn.Linear是全连接层self.linear_in = nn.Linear(3, 3)     # 输入层：3个输入特征，3个输出特征self.linear_hiden = nn.Linear(3, 2)  # 隐藏层：3个输入特征，2个输出特征self.linear_out = nn.Linear(2, 2)    # 输出层：2个输入特征，2个输出特征# 初始化网络层权重，和偏置(bias)    权重参数和偏置参数都一般使用的是PyTorch默认初始化(通常为0)# 手动初始化权重参数nn.init.kaiming_normal_(self.linear_in.weight)      # 使用Kaiming正态分布初始化输入层权重nn.init.kaiming_normal_(self.linear_hiden.weight)   # 使用Kaiming正态分布初始化隐藏层权重nn.init.kaiming_normal_(self.linear_out.weight)     # 使用Kaiming正态分布初始化输出层权重def forward(self, x):# 定义数据的前向传播路径x = self.linear_in(x)       # 数据通过输入层x = torch.relu(x)           # 应用ReLU激活函数，引入非线性x = self.linear_hiden(x)    # 数据通过隐藏层x = torch.relu(x)           # 再次应用ReLU激活函数x = self.linear_out(x)      # 数据通过输出层# 应用softmax函数将输出转换为概率分布# dim=-1 表示对最后一维进行softmax操作x = torch.softmax(x, dim=-1)return xif __name__ == '__main__':# 实例化神经网络net = Self_Net()# 创建随机输入数据：5个样本，每个样本有3个特征data = torch.randn(5, 3)# 将数据输入网络，获取输出out = net(data)print("网络输出(概率分布):")print(out)print("-------------")# 使用summary打印网络结构和参数信息# (3,)表示输入数据的形状(不包括批次维度)，batch_size=5指定批次大小summary(net, (3,), batch_size=5)print("======查看模型参数w和b======")# 遍历并打印所有可学习的参数for name, parameter in net.named_parameters():print(f"{name}: {parameter}")  # 打印参数名称和值"""
运行结果：网络输出(概率分布):
tensor([[0.8928, 0.1072],[0.8125, 0.1875],[0.8405, 0.1595],[0.7589, 0.2411],[0.5595, 0.4405]], grad_fn=<SoftmaxBackward0>)
-------------
----------------------------------------------------------------Layer (type)               Output Shape         Param #
================================================================Linear-1                     [5, 3]              12Linear-2                     [5, 2]               8Linear-3                     [5, 2]               6
================================================================
Total params: 26
Trainable params: 26
Non-trainable params: 0
----------------------------------------------------------------
Input size (MB): 0.00
Forward/backward pass size (MB): 0.00
Params size (MB): 0.00
Estimated Total Size (MB): 0.00
----------------------------------------------------------------
======查看模型参数w和b======
linear_in.weight: Parameter containing:
tensor([[ 0.7514,  1.0337,  1.0287],[-0.8729,  1.8803,  0.3209],[-0.0554, -0.0895, -0.5165]], requires_grad=True)
linear_in.bias: Parameter containing:
tensor([ 0.0469, -0.0453, -0.1729], requires_grad=True)
linear_hiden.weight: Parameter containing:
tensor([[-0.5828,  0.8744,  2.1210],[-0.9796, -0.0674, -1.3706]], requires_grad=True)
linear_hiden.bias: Parameter containing:
tensor([ 0.4696, -0.0716], requires_grad=True)
linear_out.weight: Parameter containing:
tensor([[ 0.3660, -0.7400],[-0.4122, -1.1524]], requires_grad=True)
linear_out.bias: Parameter containing:
tensor([0.4938, 0.2545], requires_grad=True)"""

4.3 模型参数计算规则

参数数量 = 权重数量 + 偏置数量，其中：

权重数量：第 l 层权重矩阵维度为（输入神经元数 × 输出神经元数）；
偏置数量：第 l 层偏置向量维度为（输出神经元数 × 1）。

以上述模型为例：

第一层（linear1）：输入 3，输出 3 → 权重 (3×3=9)，偏置 3 → 总参数 12；
第二层（linear2）：输入 3，输出 2 → 权重 (3×2=6)，偏置 2 → 总参数 8；
输出层（out）：输入 2，输出 2 → 权重 (2×2=4)，偏置 2 → 总参数 6；
模型总参数：(12+8+6=26)（与summary输出一致）。

五、损失函数：衡量模型预测误差

损失函数（Loss Function）用于量化模型预测值与真实值的差异，是模型优化的 “指南针”。不同任务（分类 / 回归）需选择不同的损失函数。

5.1 分类任务损失函数

（1）多分类交叉熵损失（CrossEntropyLoss）

适用场景：多分类任务；
原理：结合 SoftMax 函数，将预测值转换为概率后，计算真实类别与预测概率的交叉熵；从概率角度理解，我们的目的是最小化正确类别所对应的预测概率的对数的负值(损失值最小)

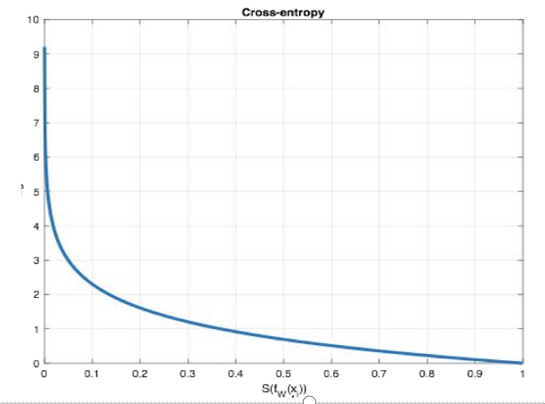
PyTorch 实现：

# 真实标签（无需独热编码，直接输入类别索引）
y_true = torch.tensor([1, 2], dtype=torch.int64)
# 模型预测分数（未经过SoftMax）
y_pred = torch.tensor([[0.2, 0.6, 0.2], [0.1, 0.8, 0.1]], dtype=torch.float32)loss_fn = nn.CrossEntropyLoss()
loss = loss_fn(y_pred, y_true)
print("多分类交叉熵损失:", loss.item())
"""
输出结果：
多分类交叉熵损失: 1.1200754642486572
"""

（2）二分类交叉熵损失（BCELoss）

适用场景：二分类任务（如垃圾邮件识别）；
原理：结合 Sigmoid 函数，计算真实标签（0/1）与预测概率的交叉熵；
注意：输入需先经过 Sigmoid 处理；
PyTorch 实现：

# 真实标签（0/1）
y_true = torch.tensor([0, 1, 0], dtype=torch.float32)
# 模型预测概率（已经过Sigmoid）
y_pred = torch.tensor([0.69, 0.55, 0.25], requires_grad=True)loss_fn = nn.BCELoss()
loss = loss_fn(y_pred, y_true)
print("二分类交叉熵损失:", loss.item())"""
输出结果：
二分类交叉熵损失: 0.6855673789978027
"""

5.2 回归任务损失函数

（1）MAE（L1 损失）

公式：

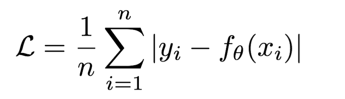
特性：对异常值鲁棒（受极端值影响小），但梯度在 0 点不连续，易跳过最优解；

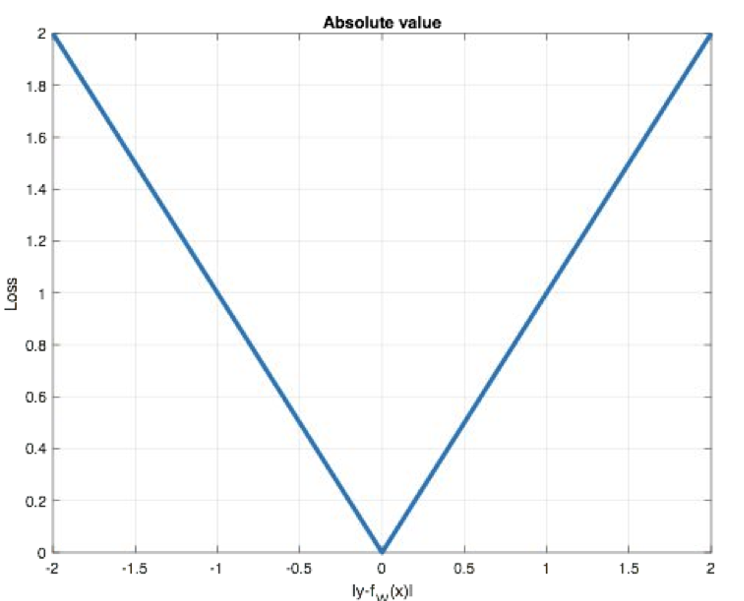
PyTorch 实现：

# 1 设置真实值和预测值
y_pred = torch.tensor([1.0, 1.0, 1.9], requires_grad=True)
y_true = torch.tensor([2.0, 2.0, 2.0], dtype=torch.float32)
# 2 实例MAE损失对象
loss = nn.L1Loss()
# 3 计算损失
my_loss = loss(y_pred, y_true).detach().numpy()
print('loss:', my_loss)"""
输出结果：
loss: 0.7
"""

（2）MSE loss（Mean Squared Loss/ Quadratic Loss也被称为L2 loss，或欧氏距离）它以误差的平方和的均值作为距离

公式：

特性：梯度连续，收敛稳定，但对异常值敏感（平方放大误差）；
当预测值与目标值相差很大时, 梯度容易爆炸。

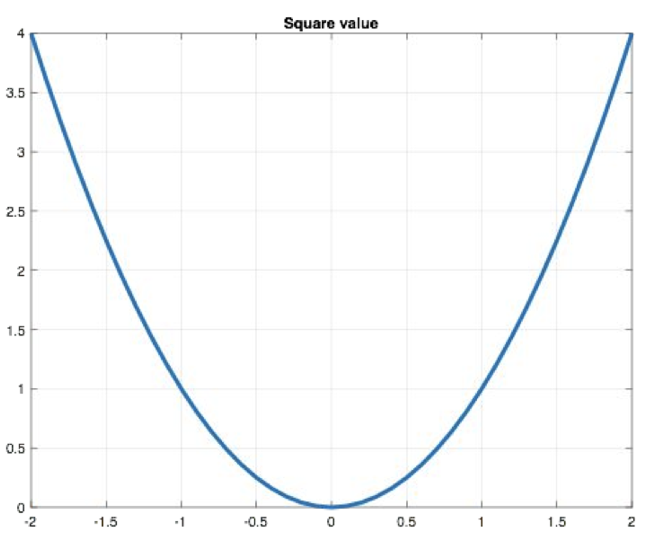
PyTorch 实现：

# 1 设置真实值和预测值
y_pred = torch.tensor([1.0, 1.0, 1.9], requires_grad=True)
y_true = torch.tensor([2.0, 2.0, 2.0], dtype=torch.float32)
# 2 实例MSE损失对象
loss = nn.MSELoss()
# 3 计算损失
my_loss = loss(y_pred, y_true).detach().numpy()
print('myloss:', my_loss)"""
输出结果：
myloss: 0.67
"""

（3）Smooth L1 损失：smooth L1说的是光滑之后的L1

公式：

特性：在[-1,1]之间实际上就是L2损失，这样解决了L1的不光滑问题
在[-1,1]区间外，实际上就是L1损失，这样就解决了离群点梯度爆炸的问题

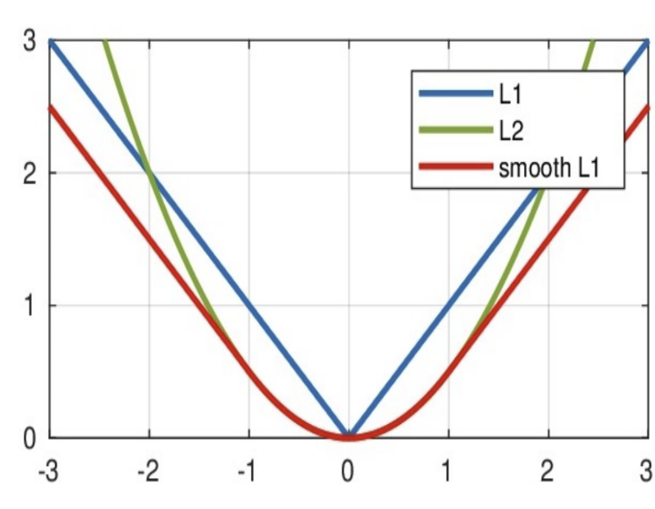
PyTorch 实现：

# 1 设置真实值和预测值
y_true = torch.tensor([0, 3])
y_pred = torch.tensor ([0.6, 0.4], requires_grad=True)
# 2 实例smmothL1损失对象
loss = nn.SmoothL1Loss()
# 3 计算损失
my_loss = loss(y_pred, y_true).detach().numpy()
print('loss:', my_loss)"""
输出结果：
loss: 1.14
"""

六、网络优化方法

优化方法的核心是通过梯度下降最小化损失函数，解决传统梯度下降中 “梯度消失、鞍点、收敛慢” 等问题。

6.1 梯度下降基础概念

Epoch：使用全部数据对模型进行以此完整训练，训练轮次
Batch Size：使用训练集中的小部分样本对模型权重进行以此反向传播的参数更新，每次训练每批次样本数量
Iteration：每使用一个 Batch 更新一次参数的过程；

示例：假设数据集有 50000 个训练样本，现在选择 Batch Size = 256 对模型进行训练。

每个 Epoch 要训练的图片数量：50000

训练集具有的 Batch 个数：50000/256+1=196

每个 Epoch 具有的 Iteration 个数：196

10个 Epoch 具有的 Iteration 个数：1960

6.2 常见梯度下降变体

方法	原理	优点	缺点
BGD（批量）	用全部数据计算梯度，更新一次参数	收敛稳定，梯度准确	数据量大时计算慢，内存占用高
SGD（随机）	用单个样本计算梯度，更新参数	计算快，适合大数据	梯度波动大，收敛不稳定
Mini-Batch	用 Batch 数据计算梯度，更新参数	平衡收敛速度与稳定性	需调优 Batch Size

6.3 进阶优化算法

梯度下降优化算法中，可能会碰到以下情况：

碰到平缓区域，梯度值较小，参数优化变慢
碰到 “鞍点” ，梯度为 0，参数无法优化
碰到局部最小值，参数不是最优

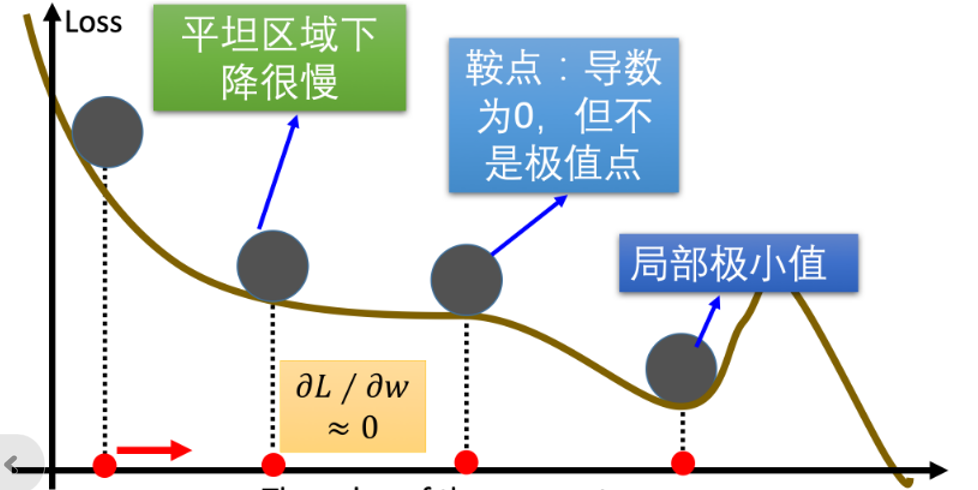
对于这些问题, 出现了一些对梯度下降算法的优化方法，

（1）指数加权平均

原理：参考各数值，并且各数值的权重都不同，距离越远的数字对平均数计算的贡献就越小（权重较小），距离越近则对平均数的计算贡献就越大（权重越大）。
公式：

代码示例

生成30个服从标准正态分布的随机数，产生 30 天的气温数据：

import torch
import  matplotlib.pyplot as plttorch.manual_seed(1) # 设置随机种子# 生成30个服从标准正态分布的随机数temps = torch.randn(size=(30,)) * 10
days = torch.arange(1, 31, 1)# 绘制原始数据
plt.scatter(days, temps)
plt.plot(days, temps,color='red')beta = 0.5 # 权重系数
#beta = 0.9 # 权重系数avg_weights = []
for i,t in enumerate(temps):if i == 0:avg_weights.append(t)continuetemp = beta*avg_weights[i-1] + (1-beta)*tavg_weights.append(temp)plt.plot(days, avg_weights,color='blue')
plt.show()

运行结果：

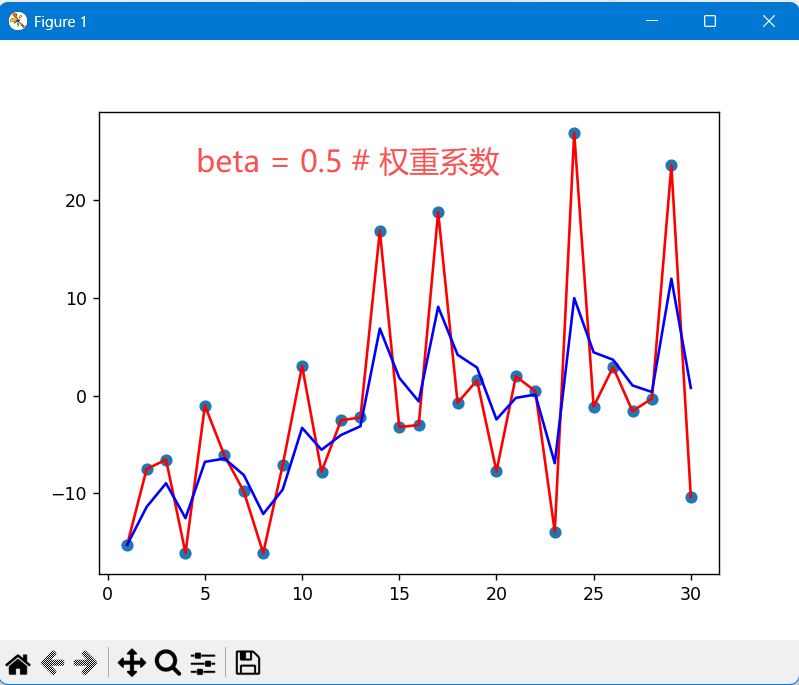
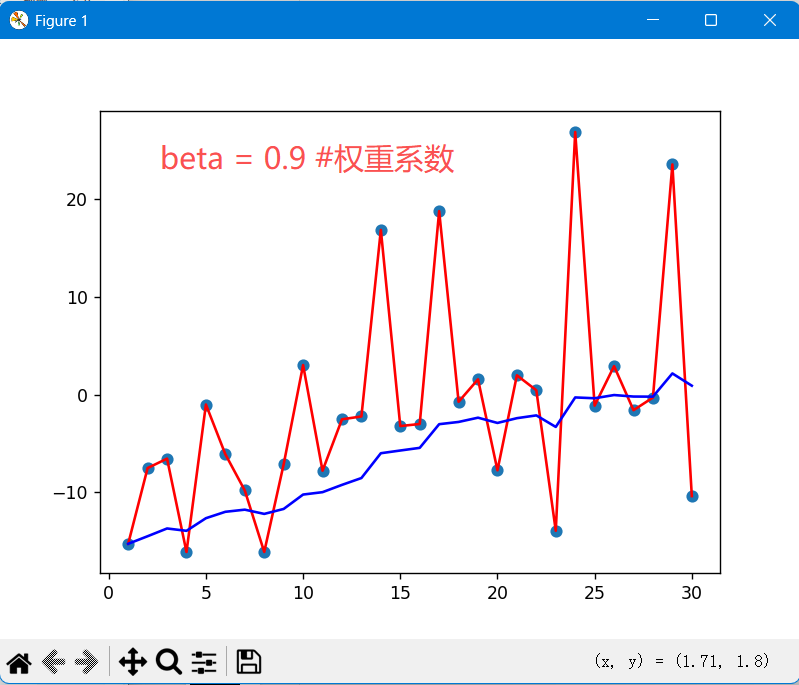
上图是β为0.5和0.9时的结果，从中可以看出：指数加权平均绘制出的气氛变化曲线更加平缓， β 的值越大，则绘制出的折线越加平缓，波动越小

（2）Momentum（动量法）

原理：引入 “动量”（历史梯度加权平均），模拟物理惯性，加速收敛并抑制震荡；
当处于鞍点位置时，由于当前的梯度为 0，参数无法更新。但是 Momentum 动量梯度下降算法已经在先前积累了一些梯度值，很有可能使得跨过鞍点。
由于 mini-batch 普通的梯度下降算法，每次选取少数的样本梯度确定前进方向，可能会出现震荡，使得训练时间变长。Momentum 使用移动加权平均，平滑了梯度的变化，使得前进方向更加平缓，有利于加快训练过程。
公式：

代码实现：

import torch# 1 初始化权重参数
w = torch.tensor([1.0], requires_grad=True, dtype=torch.float32)
y = ((w ** 2) / 2.0).sum()
# 2 实例化优化方法：SGD 指定参数beta=0.9
optimizer = torch.optim.SGD([w], lr=0.01, momentum=0.9)
# 3 第1次更新 计算梯度，并对参数进行更新
optimizer.zero_grad()
y.backward()
optimizer.step()
print('第1次: 梯度w.grad: %f, 更新后的权重:%f' % (w.grad.numpy(), w.detach().numpy()))
# 4 第2次更新 计算梯度，并对参数进行更新
# 使用更新后的参数机选输出结果
y = ((w ** 2) / 2.0).sum()
optimizer.zero_grad()
y.backward()
optimizer.step()
print('第2次: 梯度w.grad: %f, 更新后的权重:%f' % (w.grad.numpy(), w.detach().numpy()))"""
运行结果：
第1次: 梯度w.grad: 1.000000, 更新后的权重:0.990000
第2次: 梯度w.grad: 0.990000, 更新后的权重:0.971100"""

（3）AdaGrad

原理：为每个参数分配自适应学习率，频繁更新的参数学习率减小，稀疏参数学习率增大；
计算步骤：

初始化学习率 α、初始化参数 θ、小常数 σ = 1e-6
初始化梯度累积变量 s = 0
从训练集中采样 m 个样本的小批量，计算梯度 g
累积平方梯度 s = s + g ⊙ g，⊙ 表示各个分量相乘

缺点：可能会使得学习率过早、过量的降低，导致模型训练后期学习率太小，较难找到最优解。
PyTorch 实现：

# 1 初始化权重参数
w = torch.tensor([1.0], requires_grad=True, dtype=torch.float32)
y = ((w ** 2) / 2.0).sum()
# 2 实例化优化方法：adagrad优化方法
optimizer = torch.optim.Adagrad ([w], lr=0.01)
# 3 第1次更新 计算梯度，并对参数进行更新
optimizer.zero_grad()
y.backward()
optimizer.step()
print('第1次: 梯度w.grad: %f, 更新后的权重:%f' % (w.grad.numpy(), w.detach().numpy()))
# 4 第2次更新 计算梯度，并对参数进行更新
# 使用更新后的参数机选输出结果
y = ((w ** 2) / 2.0).sum()
optimizer.zero_grad()
y.backward()
optimizer.step()
print('第2次: 梯度w.grad: %f, 更新后的权重:%f' % (w.grad.numpy(), w.detach().numpy()))"""
输出结果：
第1次: 梯度w.grad: 1.000000, 更新后的权重:0.990000
第2次: 梯度w.grad: 0.990000, 更新后的权重:0.982965
"""

（4）RMSProp

原理：改进 AdaGrad，用指数移动平均替代累积平方梯度，避免学习率过早衰减；
前部分的步骤一样，最后使用指数移动平均累积历史梯度，公式如下

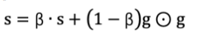
PyTorch 实现：

#修改上诉代码中的优化方法
# 1 初始化权重参数
w = torch.tensor([1.0], requires_grad=True, dtype=torch.float32)
y = ((w ** 2) / 2.0).sum()# # 2 实例化优化方法：adagrad优化方法
# optimizer = torch.optim.Adagrad ([w], lr=0.01)
# 2 实例化优化方法：RMSprop算法，其中alpha对应这beta
optimizer = torch.optim.RMSprop([w], lr=0.01,alpha=0.9)# 3 第1次更新 计算梯度，并对参数进行更新
optimizer.zero_grad()
y.backward()
optimizer.step()
print('第1次: 梯度w.grad: %f, 更新后的权重:%f' % (w.grad.numpy(), w.detach().numpy()))
# 4 第2次更新 计算梯度，并对参数进行更新
# 使用更新后的参数机选输出结果
y = ((w ** 2) / 2.0).sum()
optimizer.zero_grad()
y.backward()
optimizer.step()
print('第2次: 梯度w.grad: %f, 更新后的权重:%f' % (w.grad.numpy(), w.detach().numpy()))"""
输出结果：
第1次: 梯度w.grad: 1.000000, 更新后的权重:0.968377
第2次: 梯度w.grad: 0.968377, 更新后的权重:0.945788
"""

（5）Adam（目前最常用）

原理：Momentum 使用指数加权平均计算当前的梯度值
AdaGrad、RMSProp 使用自适应的学习率
Adam优化算法（Adaptive Moment Estimation，自适应矩估计）将 Momentum 和 RMSProp 算法结合在一起。

修正梯度: 使⽤梯度的指数加权平均
修正学习率: 使⽤梯度平⽅的指数加权平均。

PyTorch 实现：

# 1 初始化权重参数
w = torch.tensor([1.0], requires_grad=True, dtype=torch.float32)
y = ((w ** 2) / 2.0).sum()# # 2 实例化优化方法：adagrad优化方法
# optimizer = torch.optim.Adagrad ([w], lr=0.01)
# 2 实例化优化方法：RMSprop算法，其中alpha对应这beta
# optimizer = torch.optim.RMSprop([w], lr=0.01,alpha=0.9)
# 2 实例化优化方法：Adam算法，其中betas是指数加权的系数
optimizer = torch.optim.Adam([w], lr=0.01,betas=[0.9,0.99])# 3 第1次更新 计算梯度，并对参数进行更新
optimizer.zero_grad()
y.backward()
optimizer.step()
print('第1次: 梯度w.grad: %f, 更新后的权重:%f' % (w.grad.numpy(), w.detach().numpy()))
# 4 第2次更新 计算梯度，并对参数进行更新
# 使用更新后的参数机选输出结果
y = ((w ** 2) / 2.0).sum()
optimizer.zero_grad()
y.backward()
optimizer.step()
print('第2次: 梯度w.grad: %f, 更新后的权重:%f' % (w.grad.numpy(), w.detach().numpy()))"""
输出结果：
第1次: 梯度w.grad: 1.000000, 更新后的权重:0.990000
第2次: 梯度w.grad: 0.990000, 更新后的权重:0.980003
"""

6.4 学习率衰减策略

学习率过大易跳过最优解，过小则收敛慢。通过衰减策略动态调整学习率：

1.等间隔衰减（StepLR）：每间隔一定 Epoch，学习率乘以衰减系数；

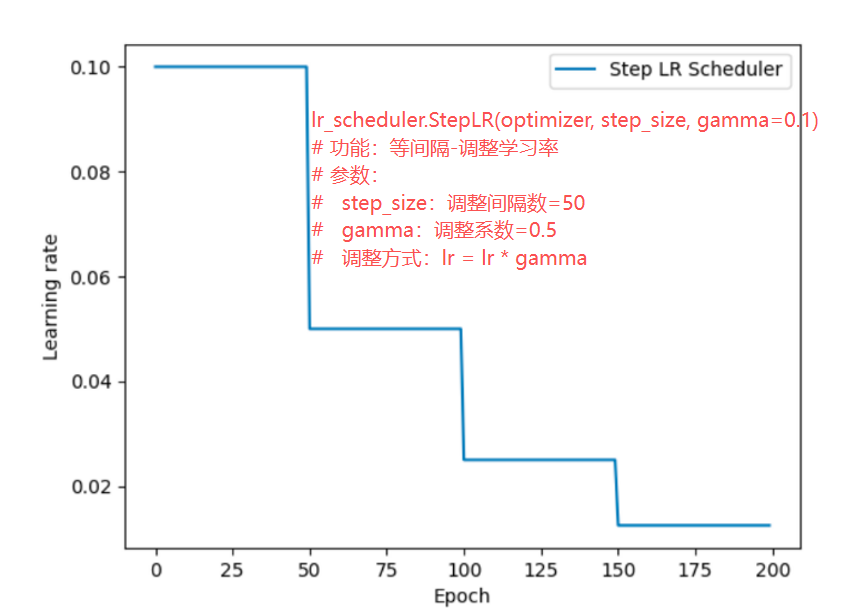
scheduler = torch.optim.lr_scheduler.StepLR(optimizer, step_size=50, gamma=0.5)

2.指定间隔衰减（MultiStepLR）：在预设 Epoch 处衰减学习率；

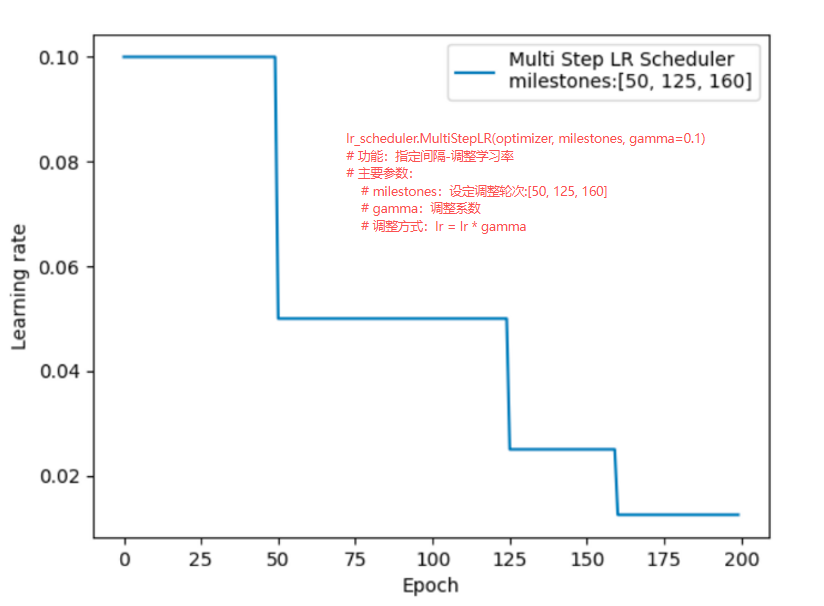
scheduler = torch.optim.lr_scheduler.MultiStepLR(optimizer, milestones=[50, 125], gamma=0.5)

3.指数衰减（ExponentialLR）：学习率随 Epoch 指数衰减

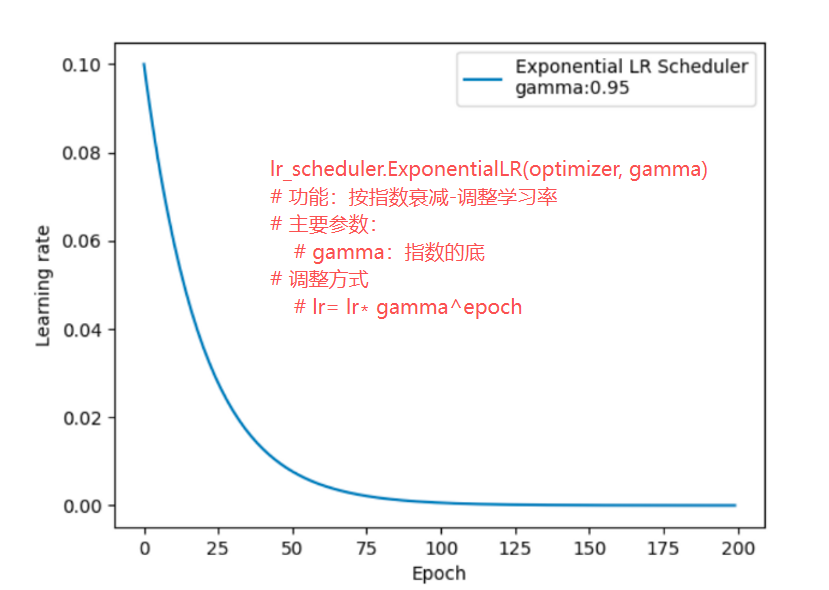
scheduler = torch.optim.lr_scheduler.ExponentialLR(optimizer, gamma=0.95)

用具体代码实现：

import torch
import torch.optim as optim
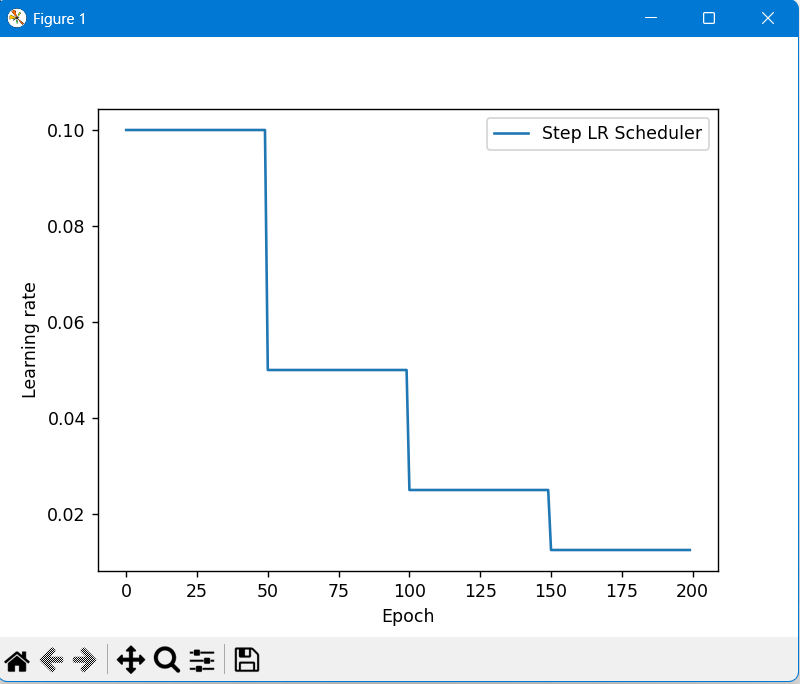
import matplotlib.pyplot as pltdef test_StepLR():# 0.参数初始化LR = 0.1  # 设置学习率初始化值为0.1iteration = 10max_epoch = 200# 1 初始化参数y_true = torch.tensor([0])x = torch.tensor([1.0])w = torch.tensor([1.0], requires_grad=True)# 2.优化器optimizer = optim.SGD([w], lr=LR, momentum=0.9)# 3.设置学习率下降策略scheduler_lr = optim.lr_scheduler.StepLR(optimizer, step_size=50, gamma=0.5)# 4.获取学习率的值和当前的epochlr_list, epoch_list = list(), list()for epoch in range(max_epoch):lr_list.append(scheduler_lr.get_last_lr()) # 获取当前lrepoch_list.append(epoch) # 获取当前的epochfor i in range(iteration): # 遍历每一个batch数据loss = ((w*x-y_true)**2)/2.0 # 目标函数optimizer.zero_grad()# 反向传播loss.backward()optimizer.step()# 更新下一个epoch的学习率scheduler_lr.step()# 5.绘制学习率变化的曲线plt.plot(epoch_list, lr_list, label="Step LR Scheduler")plt.xlabel("Epoch")plt.ylabel("Learning rate")plt.legend()plt.show()def test_MultiStepLR():torch.manual_seed(1)LR = 0.1iteration = 10max_epoch = 200weights = torch.randn((1), requires_grad=True)target = torch.zeros((1))print('weights-->', weights, 'target-->', target)optimizer = optim.SGD([weights], lr=LR, momentum=0.9)# 设定调整时刻数milestones = [50, 125, 160]# 设置学习率下降策略scheduler_lr = optim.lr_scheduler.MultiStepLR(optimizer, milestones=milestones, gamma=0.5)lr_list, epoch_list = list(), list()for epoch in range(max_epoch):lr_list.append(scheduler_lr.get_last_lr())epoch_list.append(epoch)for i in range(iteration):loss = torch.pow((weights - target), 2)optimizer.zero_grad()# 反向传播loss.backward()# 参数更新optimizer.step()# 更新下一个epoch的学习率scheduler_lr.step()plt.plot(epoch_list, lr_list, label="Multi Step LR Scheduler\nmilestones:{}".format(milestones))plt.xlabel("Epoch")plt.ylabel("Learning rate")plt.legend()plt.show()def test_ExponentialLR():# 0.参数初始化LR = 0.1  # 设置学习率初始化值为0.1iteration = 10max_epoch = 200# 1 初始化参数y_true = torch.tensor([0])x = torch.tensor([1.0])w = torch.tensor([1.0], requires_grad=True)# 2.优化器optimizer = optim.SGD([w], lr=LR, momentum=0.9)# 3.设置学习率下降策略gamma = 0.95scheduler_lr = optim.lr_scheduler.ExponentialLR(optimizer, gamma=gamma)# 4.获取学习率的值和当前的epochlr_list, epoch_list = list(), list()for epoch in range(max_epoch):lr_list.append(scheduler_lr.get_last_lr())epoch_list.append(epoch)for i in range(iteration): # 遍历每一个batch数据loss = ((w*x-y_true)**2)/2.0optimizer.zero_grad()# 反向传播loss.backward()optimizer.step()# 更新下一个epoch的学习率scheduler_lr.step()# 5.绘制学习率变化的曲线plt.plot(epoch_list, lr_list, label="Exponential LR Scheduler")  # 修正了标签名称plt.xlabel("Epoch")plt.ylabel("Learning rate")plt.legend()plt.show()# 运行测试函数
if __name__ == "__main__":test_StepLR()test_MultiStepLR()test_ExponentialLR()

运行结果：

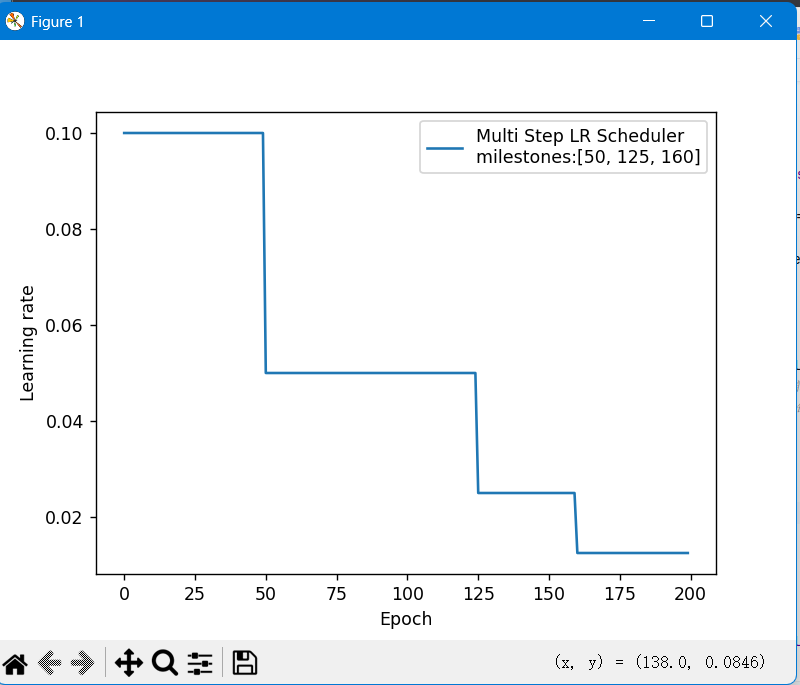
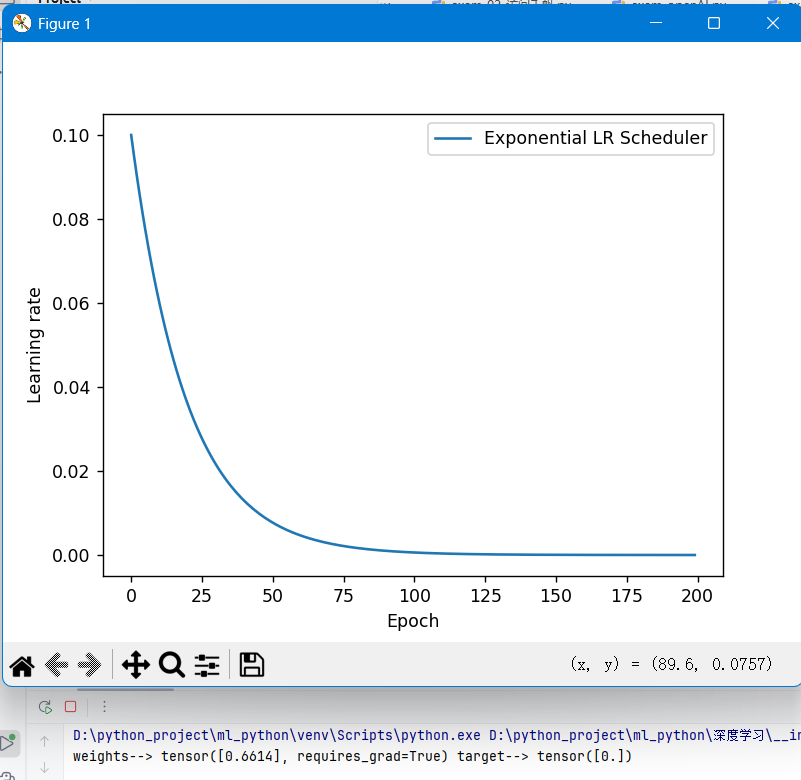
七、正则化：缓解过拟合

过拟合是指模型在训练集上表现好，但在测试集上泛化能力差。正则化通过限制模型复杂度，提升泛化能力。

7.1 Dropout（随机失活）

原理：在训练过程中，Dropout的实现是让神经元以超参数p的概率停止工作或者激活被置为0,未被置为0的进行缩放，缩放比例为1/(1-p)。
训练过程可以认为是对完整的神经网络的一些子集进行训练，每次基于输入数据只更新子网络的参数。；
测试时，所有神经元正常工作，无需缩放；
作用：防止神经元过度依赖某几个输入特征，减少过拟合；
PyTorch 实现：

class NetWithDropout(nn.Module):def __init__(self):super().__init__()self.linear1 = nn.Linear(10, 20)self.dropout = nn.Dropout(p=0.4)  # 40%概率失活self.linear2 = nn.Linear(20, 2)def forward(self, x):x = torch.relu(self.linear1(x))x = self.dropout(x)  # 训练时自动生效，测试时需用model.eval()关闭x = torch.softmax(self.linear2(x), dim=-1)return x

7.2 批量归一化（BN 层）

原理：对每一层的输入进行标准化（均值为 0，方差为 1），再通过可学习参数λ 缩放，β 平移重构数据分布；
公式：

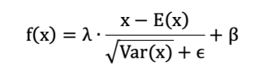
λ 和 β 是可学习的参数，它相当于对标准化后的值做了一个线性变换，λ 为系数，β 为偏置；

eps 通常指为 1e-5，避免分母为 0； E(x) 表示变量的均值； Var(x) 表示变量的方差

作用：加速训练收敛，缓解梯度消失，降低对初始化的敏感度；
PyTorch 实现：

class NetWithBN(nn.Module):def __init__(self):super().__init__()self.linear1 = nn.Linear(10, 20)self.bn = nn.BatchNorm1d(20)  # 1D BN层，输入维度20self.linear2 = nn.Linear(20, 2)def forward(self, x):x = self.linear1(x)x = self.bn(x)  # 标准化+重构x = torch.relu(x)x = torch.softmax(self.linear2(x), dim=-1)return x

八、实战案例：手机价格分类

8.1 需求分析

基于二手手机的 20 个特征（如电池容量、RAM、摄像头像素等），预测手机价格区间（0-3，共 4 类），属于多分类任务。

8.2 数据准备

数据集：2000 条样本，含 20 个特征和 1 个标签（price_range）；
划分：70%（1600 条）为训练集，30%（400 条）为测试集；
工具：使用pandas读取数据，sklearn划分数据集，PyTorch构建数据加载器。

8.3 模型构建

构建 4层全连接神经网络，使用 ReLU 激活函数，输出层用 SoftMax：

8.4 模型训练

损失函数：多分类交叉熵（CrossEntropyLoss）；
优化器：adam（学习率 0.01）；
训练轮次：300 Epoch,(引用了早停机制，在达到最优模型时自动停止训练，保存模型)
批量大小：64（最好是2的指数）。

8.5 模型评估

使用测试集评估模型准确率

整体代码如下：

训练模型

import pandas as pd
import torch
from matplotlib import pyplot as plt
from sklearn.model_selection import train_test_split
from torch import relu
from torch.nn import Linear, Module
from torch.utils.data import TensorDataset, DataLoader
from torchsummary import summary
from torch.optim import SGD, Adam, AdamWplt.rcParams['axes.unicode_minus'] = False  # 解决负号'-'显示为方块的问题
plt.rcParams['font.sans-serif'] = ['SimHei']  # 设置字体，正确显示中文# 数据显示的行数和列数
pd.set_option('display.max_rows', 5000)
pd.set_option('display.max_columns', 10000)
pd.set_option('display.width', 9000)#数据加载和预处理
def load_and_preprocess_data():# 数据读取data = pd.read_csv('../data/手机价格预测.csv')# print(data.head(5))# print(data.info())x = data.iloc[:, :-1]y = data.iloc[:, -1]# 标准化# x = (x - x.mean()) / x.std()x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.3, random_state=42)# 将数据转换为PyTorch张量x_train = torch.tensor(x_train.values, dtype=torch.float32)x_test = torch.tensor(x_test.values, dtype=torch.float32)# 多分类模型， 标签数据需要转换为long类型，表示类别索引y_train = torch.tensor(y_train.values, dtype=torch.long)y_test = torch.tensor(y_test.values, dtype=torch.long)return x_train, x_test, y_train, y_test# 创建数据加载器
def create_data_loaders(x_train, y_train, x_test, y_test):# 创建TensorDataset对象# 将 “特征张量” 和 “标签张量” 绑定为一个数据集对象，确保每次取数据时，特征和对应的标签能一一对应。train_dataset = TensorDataset(x_train, y_train)test_dataset = TensorDataset(x_test, y_test)# 初始化数据加载器# 将TensorDataset为可迭代的 “批量数据生成器”，每次迭代返回一批（batch_size个）样本，避免手动处理批量逻辑。# shuffle参数设置为True表示每次迭代时，将数据集打乱顺序，以打乱数据集的顺序，避免模型过拟合。data_loader = DataLoader(train_dataset, batch_size=64, shuffle=True)test_loader = DataLoader(test_dataset, batch_size=64, shuffle=False)return train_dataset,test_dataset,data_loader, test_loader# 定义模型
class PirceModule(Module):def __init__(self):super(PirceModule, self).__init__()self.layer_1 = Linear(20, 128)self.layer_2 = Linear(128, 256)self.layer_2_ = Linear(256, 512)self.layer_3 = Linear(512, 4)def forward(self, x):x = relu(self.layer_1(x))x = relu(self.layer_2(x))x = relu(self.layer_2_(x))x = self.layer_3(x)#默认softmax激活函数return x# 训练函数
def train_model(model, data_loader, loss_func, optimizer, train_dataset,patience=10):# 训练模型epochs = 300train_losses = [] # 训练损失best_loss = 9999.9 # 最佳损失counter = 0best_model_state = Nonefor epoch in range(epochs):# 训练阶段model.train()total_train_loss = 0for x, y in data_loader:# 前向传播output = model(x)# 计算损失loss = loss_func(output, y)# 反向传播optimizer.zero_grad()loss.backward()# 更新参数optimizer.step()total_train_loss += loss.item() * len(x)avg_train_loss = total_train_loss / len(train_dataset)train_losses.append(avg_train_loss)print(f"第{epoch + 1}轮训练，平均训练损失: {avg_train_loss:.4f}")# 早停机制if avg_train_loss < best_loss:best_loss = avg_train_lossbest_model_state = model.state_dict().copy()counter = 0print(f"训练损失改善，当前最佳损失: {best_loss}")else:counter += 1print(f"训练损失第{counter}次未改善，第{patience}次时将停止训练")print("---------")if counter >= patience:print(f"早停触发，在第{epoch + 1}轮停止训练")break# 加载最佳模型if best_model_state is not None:model.load_state_dict(best_model_state)print(f"训练完成，最佳训练损失: {best_loss}")return train_losses# 绘制损失曲线
def plot_losses(train_loss):# 绘制训练损失图plt.figure(figsize=(10, 6))plt.plot(train_loss, label='训练损失')plt.title('训练损失图')plt.xlabel('轮数')plt.ylabel('损失值')plt.legend()plt.grid(True)plt.show()# 保存模型
def save_model(model, filename="phone_predict_model.pth"):torch.save(model.state_dict(), filename)print(f"模型已保存为 {filename}")# 主函数
if __name__ == '__main__':# 设置随机种子以确保结果可重现torch.manual_seed(42)# 创建模型对象model = PirceModule()# 自定义损失函数loss_func = torch.nn.CrossEntropyLoss()# 定义优化器optimizer = torch.optim.Adam(model.parameters(), lr=0.01)# 加载和预处理数据x_train, x_test, y_train, y_test = load_and_preprocess_data()# 创建数据加载器train_dataset, test_dataset, data_loader, test_loader = create_data_loaders(x_train, y_train, x_test, y_test)# 训练模型train_loss= train_model(model, data_loader, loss_func, optimizer, train_dataset)plot_losses(train_loss)save_model(model)

测试模型：

import torch
from torch.utils.data import DataLoader
from New_phone_train import PirceModule, load_and_preprocess_data, create_data_loaders# 加载和预处理数据
x_train, x_test, y_train, y_test = load_and_preprocess_data()
# 创建数据加载器
train_dataset, test_dataset, data_loader, test_loader = create_data_loaders(x_train, y_train, x_test, y_test)model = PirceModule()model.load_state_dict(torch.load("phone_predict_model.pth"))correct = 0
for x,y in test_loader:y_pred_ = model(x)y_pred = torch.argmax(y_pred_,dim=1)correct += (y_pred == y).sum()print("准确率：", correct / len(test_dataset))"""
打印结果：
准确率： tensor(0.9200)
"""

8.6 模型调优建议

一般来说，模型的优化方法：

优化器：将 SGD 替换为 Adam；
学习率：调整为 0.0001，并使用学习率衰减；
数据预处理：对特征进行标准化（如均值归一化）；
模型改进：增加 BN 层、Dropout 层，或加深网络；
超参数调优：调整 Batch Size（如 16/32/64/128）、训练轮次（如 100）、添加早停机制等等。

九、神经网络的优缺点

优点	缺点
拟合能力强，可逼近任意非线性函数	模型 “黑箱”，难以解释预测逻辑
精度高，在图像、NLP 等领域超越传统方法	训练时间长，需大量计算资源（GPU）
自动化特征学习，无需人工设计特征	网络结构复杂，超参数调优难度大
有丰富的框架支持（PyTorch/TensorFlow）	小数据集易过拟合，依赖大量标注数据

十、总结

本文从神经网络的基础概念出发，系统讲解了激活函数、参数初始化、损失函数、优化方法、正则化等核心技术，并通过手机价格分类案例完成了从理论到实践的落地。神经网络的学习需要 “理论 + 代码” 结合，建议读者结合本文代码反复调试，逐步掌握超参数调优、模型改进等实战技巧。后续可进一步学习卷积神经网络（CNN）、循环神经网络（RNN）等更复杂的网络结构，探索深度学习在计算机视觉、自然语言处理等领域的应用