数据结构(C语言篇):(十五)二叉树OJ题
目录
前言
一、单值二叉树
1.1 题目分析
1.2 核心解题思路
1.3 详细解题步骤与代码实现
1.3.1 前提:二叉树节点结构定义
1.3.2 方法一:递归遍历
(1)解题步骤
(2)代码实现与详解
(3)关键细节
1.3.3 方法二:迭代遍历(BFS / 层序遍历)
(1)解题步骤
(2)代码实现与详解
(3)关键细节
二、相同的树
2.1 题目分析
2.2 核心解题思路
2.3 详细解题步骤与代码实现
2.3.1 递归遍历
(1)解题步骤
(2)代码实现与详解
(3)关键细节
2.3.2 迭代遍历(BFS / 层序遍历)
(1)解题步骤
(2)代码实现与详解(使用队列辅助)
(3)关键细节
三、对称二叉树
3.1 题目分析
3.2 核心解题思路
3.3 详细解题步骤与代码实现
3.3.1 方法一:递归法
(1)解题步骤
(2)代码实现与详解
(3)关键细节
3.3.2 方法二:迭代法(BFS / 队列实现)
(1)解题步骤
(2)代码实现与详解(需队列辅助)
(3)关键细节
四、另一棵树的子树
4.1 题目分析
4.2 核心解题思路
4.3 详细解题步骤与代码实现
4.3.1 核心辅助函数:判断两棵树是否相同(复用“相同的树”逻辑)
4.3.2 方法一:递归法
(1)解题步骤
(2)代码实现与详解
(3)关键细节
4.3.3 方法二:迭代法(DFS / 栈实现)
(1)解题步骤
(2)代码实现与详解(用栈辅助)
(3)关键细节
五、二叉树性质补充
总结
前言
在学习完二叉树的一些相关函数的实现之后,相信大家都很想做一些题目来实战一下吧!本期博客,博主就为大家带来了一些优质好题,让我们一起来加深一下对二叉树的理解,现在正式开始吧!
一、单值二叉树

题目链接:https://leetcode.cn/problems/univalued-binary-tree/description/
1.1 题目分析
题目要求:判断一棵二叉树是否为「单值二叉树」—— 即树中所有节点的值都相同,是则返回true,否则返回false。
题目还给出了如下的约束条件:
- 树的节点数范围:
[1, 100](根节点必存在,无需处理空树边界); - 节点值范围:
[0, 99](整数类型)。
1.2 核心解题思路
单值二叉树的本质是“所有节点的值与根节点的值一致”,因此我们解题的核心思路是:
1. 确定基准值:以根节点的值为target(所有节点需与之相等);以根节点的值为target(所有节点需与之相等);
2. 遍历全树检查:通过「递归遍历」或「迭代遍历」(DFS/BFS)逐个检查节点值,若存在任意节点值≠target,直接返回false;全部检查通过则返回true。
这里我们给出两种主流的遍历方式:
- 递归:利用二叉树的递归结构(每个子树也是二叉树),代码简洁直观,适合题目节点数较少的场景;
- 迭代:通过栈(DFS)或队列(BFS)手动维护遍历顺序,避免递归栈溢出风险(虽题目节点数少, but 通用解法)。
1.3 详细解题步骤与代码实现
1.3.1 前提:二叉树节点结构定义
LeetCode 中其实已经为我们预设了节点结构,这里为了清晰展示逻辑,补充定义如下:
// 二叉树节点结构
typedef struct TreeNode {int val; // 节点值struct TreeNode *left; // 左子节点struct TreeNode *right; // 右子节点
} TreeNode;1.3.2 方法一:递归遍历
(1)解题步骤
1. 记录基准值:获取根节点的值target(所有节点需匹配此值);获取根节点的值target(所有节点需匹配此值)。
2. 定义递归检查函数:
- 终止条件 1:若当前节点为
NULL(空子树,无节点需检查)→ 返回true; - 终止条件 2:若当前节点值≠
target(找到不匹配节点)→ 返回false; - 递归逻辑:当前节点匹配时,需同时递归检查左子树和右子树(二者均需匹配才返回
true)。
3. 调用递归函数:从根节点开始检查,返回最终结果。
(2)代码实现与详解
bool isUnivalTree(TreeNode* root) {// 步骤1:确定基准值(根节点值,题目保证root非空)int target = root->val;// 步骤2:定义递归辅助函数(检查当前节点及其子树)// 函数功能:判断以node为根的子树是否所有节点值为targetbool check(TreeNode* node) {// 终止条件1:空节点,无需检查,返回trueif (node == NULL) {return true;}// 终止条件2:节点值不匹配,返回falseif (node->val != target) {return false;}// 递归检查左子树 AND 右子树(需两者都满足)return check(node->left) && check(node->right);}// 步骤3:从根节点开始检查,返回结果return check(root);
}(3)关键细节
- 递归的「短路特性」:若左子树检查返回
false,则不会再递归检查右子树(直接返回false),能够大大提升效率。 - 空节点返回
true的原因:空子树是 “合法” 的(没有不匹配节点),例如示例 1 中根节点的右子树有一个null节点,是不影响结果的。
1.3.3 方法二:迭代遍历(BFS / 层序遍历)
(1)解题步骤
1. 记录基准值:同方法 1,获取根节点值target。
2. 初始化队列:用队列实现 BFS(层序遍历),先将根节点入队。
3. 循环遍历队列:
- 出队头节点:取出当前要检查的节点;
- 检查节点值:若≠
target,直接返回false; - 入队子节点:若左 / 右子节点非空,依次入队,确保后续检查。
4. 队列遍历结束:所有节点均匹配,返回true。
(2)代码实现与详解
// 先实现队列的基础操作(适配TreeNode*类型)
typedef struct QueueNode {TreeNode* data; // 队列存储二叉树节点指针struct QueueNode* next; // 队列节点的下一个节点
} QueueNode;typedef struct Queue {QueueNode* front; // 队头(出队)QueueNode* rear; // 队尾(入队)
} Queue;// 队列初始化:空队列,队头队尾均为NULL
void QueueInit(Queue* q) {q->front = q->rear = NULL;
}// 入队:从队尾添加元素
void QueuePush(Queue* q, TreeNode* val) {QueueNode* newNode = (QueueNode*)malloc(sizeof(QueueNode));newNode->data = val;newNode->next = NULL;if (q->rear == NULL) { // 队列空时,队头队尾指向新节点q->front = q->rear = newNode;} else { // 队列非空时,队尾链接新节点并更新队尾q->rear->next = newNode;q->rear = newNode;}
}// 出队:从队头删除元素(需确保队列非空)
void QueuePop(Queue* q) {if (q->front == NULL) return; // 空队列无需出队QueueNode* temp = q->front; // 暂存队头节点q->front = q->front->next; // 队头后移if (q->front == NULL) { // 若出队后队列空,队尾也置为NULLq->rear = NULL;}free(temp); // 释放原队头节点的内存
}// 判空:队列是否为空
bool QueueEmpty(Queue* q) {return q->front == NULL;
}// 获取队头元素(需确保队列非空)
TreeNode* QueueFront(Queue* q) {return q->front->data;
}// 销毁队列:释放所有队列节点内存
void QueueDestroy(Queue* q) {while (!QueueEmpty(q)) {QueuePop(q);}
}// 核心:单值二叉树判断(BFS迭代版)
bool isUnivalTree(TreeNode* root) {if (root == NULL) return true; // 题目保证root非空,此处为通用处理// 步骤1:记录基准值int target = root->val;// 步骤2:初始化队列,根节点入队Queue q;QueueInit(&q);QueuePush(&q, root);// 步骤3:循环遍历队列while (!QueueEmpty(&q)) {// 3.1 出队头节点TreeNode* curr = QueueFront(&q);QueuePop(&q);// 3.2 检查当前节点值:不匹配则返回falseif (curr->val != target) {QueueDestroy(&q); // 销毁队列避免内存泄漏return false;}// 3.3 子节点非空则入队(继续检查后续节点)if (curr->left != NULL) {QueuePush(&q, curr->left);}if (curr->right != NULL) {QueuePush(&q, curr->right);}}// 步骤4:所有节点检查通过,销毁队列并返回trueQueueDestroy(&q);return true;
}(3)关键细节
- 队列的作用:确保按「层序」遍历所有节点,不遗漏任何一个;
- 内存安全:每次返回前必须销毁队列(
QueueDestroy),避免队列节点的内存泄漏; - 与递归的对比:迭代版无递归栈溢出风险,适合节点数极多的树(本题无需,但是是通用的)。
二、相同的树
题目链接:https://leetcode.cn/problems/same-tree/description/
2.1 题目分析
题目要求:判断两棵二叉树是否「相同」—— 需同时满足两个条件:① 结构完全一致(对应位置的节点存在性相同);② 对应节点的值完全相等,是则返回true,否则返回false。
约束条件:
- 两棵树的节点数范围:
[0, 100](允许空树,需处理 “两棵都空”“一棵空一棵非空” 的边界); - 节点值范围:
[-10⁴, 10⁴](整数类型,需支持负数对比)。
2.2 核心解题思路
“相同树” 的本质是「两棵树的节点在 “位置” 和 “值” 上完全对齐」,因此核心思路是同步遍历两棵树,每一步对「对应位置的节点」做双重检查:
- 结构检查:判断当前位置的两个节点是否 “同时存在” 或 “同时不存在”(若一个存在、一个不存在,则结构不一致);
- 值检查:若两个节点均存在,判断其值是否相等(值不等则直接不相同)。
我们同样也可以分别使用递归和迭代两种遍历方式实现:
2.3 详细解题步骤与代码实现
2.3.1 递归遍历
(1)解题步骤
递归的核心是 “分而治之”:将 “判断整棵树相同” 拆解为 “判断根节点相同 + 左子树相同 + 右子树相同”,终止条件覆盖所有边界情况:
1. 边界条件处理:
- 若两棵树的当前节点均为
NULL(同时不存在)→ 结构一致,返回true; - 若其中一棵的当前节点为
NULL、另一棵非NULL(一存一失)→ 结构不一致,返回false。
2. 值检查:若两个节点均存在,但值不相等 → 返回false。
3. 递归深入:当前节点检查通过后,递归判断「p 的左子树与 q 的左子树」和「p 的右子树与 q 的右子树」(需两者均相同,故用 “与运算” 连接)。
(2)代码实现与详解
bool isSameTree(TreeNode* p, TreeNode* q) {// 步骤1:处理边界条件(结构检查)// 情况1:两棵树当前节点都为空 → 结构一致,返回trueif (p == NULL && q == NULL) {return true;}// 情况2:一棵空、一棵非空 → 结构不一致,返回falseif (p == NULL || q == NULL) {return false;}// 步骤2:值检查(均非空时对比值)if (p->val != q->val) {return false;}// 步骤3:递归深入左子树和右子树(需两者均相同才返回true)return isSameTree(p->left, q->left) && isSameTree(p->right, q->right);
}(3)关键细节
- 终止条件的顺序:必须先判断 “是否为空”,再判断 “值是否相等”—— 若先判断值,会对
NULL节点解引用(p->val),导致程序崩溃; - 递归的 “与运算” 逻辑:只有左子树和右子树同时相同,整棵树才相同。例如示例 3 中,左子树对比返回
false,则无需再判断右子树,直接返回false(对短路进行的优化)。
2.3.2 迭代遍历(BFS / 层序遍历)
(1)解题步骤
迭代的核心是 “同步入队、同步出队”:用队列存储两棵树的「对应节点对」,每次取出一对节点做检查,再将它们的左、右子节点成对入队,确保遍历顺序完全同步:
1. 初始化队列:将两棵树的根节点p和q作为 “第一对节点” 入队。
2. 循环处理队列:
- 出队:取出队头的两个节点(
currP为 p 的当前节点,currQ为 q 的当前节点); - 检查:按 “边界条件(结构)→ 值” 的顺序判断,若不满足直接返回
false; - 入队:将
currP的左子节点与currQ的左子节点、currP的右子节点与currQ的右子节点成对入队(确保下一轮处理对应位置)。
3. 队列遍历结束:所有节点对均检查通过,返回true。
(2)代码实现与详解(使用队列辅助)
首先实现适配 “节点对” 的队列(存储TreeNode*类型,每次处理两个元素):
// 队列节点结构(存储二叉树节点指针)
typedef struct QueueNode {TreeNode* data;struct QueueNode* next;
} QueueNode;// 队列结构(队头出、队尾入)
typedef struct Queue {QueueNode* front;QueueNode* rear;
} Queue;// 队列初始化:空队列,队头队尾均为NULL
void QueueInit(Queue* q) {q->front = q->rear = NULL;
}// 入队:从队尾添加元素
void QueuePush(Queue* q, TreeNode* val) {QueueNode* newNode = (QueueNode*)malloc(sizeof(QueueNode));newNode->data = val;newNode->next = NULL;if (q->rear == NULL) { // 空队列时,队头队尾指向新节点q->front = q->rear = newNode;} else { // 非空队列时,链接新节点并更新队尾q->rear->next = newNode;q->rear = newNode;}
}// 出队:从队头删除元素(需确保队列非空)
void QueuePop(Queue* q) {if (q->front == NULL) return;QueueNode* temp = q->front;q->front = q->front->next;if (q->front == NULL) { // 出队后为空,队尾置NULLq->rear = NULL;}free(temp); // 释放原队头内存
}// 判空:队列是否为空
bool QueueEmpty(Queue* q) {return q->front == NULL;
}// 获取队头元素(需确保队列非空)
TreeNode* QueueFront(Queue* q) {return q->front->data;
}// 销毁队列:释放所有队列节点内存
void QueueDestroy(Queue* q) {while (!QueueEmpty(q)) {QueuePop(q);}
}再实现核心的 “相同树判断” 逻辑:
bool isSameTree(TreeNode* p, TreeNode* q) {// 初始化队列,将p和q作为第一对节点入队Queue qNode;QueueInit(&qNode);QueuePush(&qNode, p);QueuePush(&qNode, q);// 循环处理队列中的节点对while (!QueueEmpty(&qNode)) {// 步骤1:出队一对节点(currP对应p的节点,currQ对应q的节点)TreeNode* currP = QueueFront(&qNode);QueuePop(&qNode);TreeNode* currQ = QueueFront(&qNode);QueuePop(&qNode);// 步骤2:结构检查(边界条件)if (currP == NULL && currQ == NULL) {continue; // 均为空,无需后续检查,跳过当前轮}if (currP == NULL || currQ == NULL) {QueueDestroy(&qNode); // 销毁队列避免内存泄漏return false; // 一存一失,结构不同}// 步骤3:值检查(均非空时对比值)if (currP->val != currQ->val) {QueueDestroy(&qNode);return false;}// 步骤4:将下一对节点入队(左子树对 + 右子树对)QueuePush(&qNode, currP->left);QueuePush(&qNode, currQ->left);QueuePush(&qNode, currP->right);QueuePush(&qNode, currQ->right);}// 所有节点对均检查通过QueueDestroy(&qNode);return true;
}(3)关键细节
- 节点对的入队顺序:必须严格按照 “p 的左 → q 的左 → p 的右 → q 的右” 入队,确保下一轮处理的是 “对应位置的子节点”—— 若顺序错误(如 p 的左和 q 的右入队),会导致结构对比错位。
- 队列的内存安全:无论返回
true还是false,都必须调用QueueDestroy释放队列内存,避免队列节点的内存泄漏。 - 空节点的处理:当一对节点均为空时,用
continue跳过后续检查(无需入队子节点,因为空节点没有子节点),避免无效操作。
三、对称二叉树
题目链接:https://leetcode.cn/problems/symmetric-tree/description/
3.1 题目分析
题目要求:判断一棵二叉树是否「轴对称」—— 即树的左子树与右子树呈「镜像对称」(结构一致且对称位置的节点值相等),是则返回true,否则返回false。
约束条件:
- 树的节点数范围:
[1, 1000](根节点必存在,需处理 “左 / 右子树为空” 的边界); - 节点值范围:
[-100, 100](支持负数对比)。
3.2 核心解题思路
“对称二叉树” 的本质不是 “树与自身相同”,而是左子树与右子树镜像。镜像的核心条件是:
- 根值相等:左子树的根节点值 = 右子树的根节点值;
- 结构镜像:左子树的「左孩子」对应右子树的「右孩子」,左子树的「右孩子」对应右子树的「左孩子」;
- 递归满足:所有对称位置的子树均需满足上述两点。
下面我同样也用递归法和迭代法两种方法解题。
3.3 详细解题步骤与代码实现
3.3.1 方法一:递归法
(1)解题步骤
递归的核心是 “拆分镜像检查”:用辅助函数接收两个节点(左子树的某节点、右子树的对称节点),按以下逻辑判断:
1. 边界条件处理:
- 若两个节点均为
NULL(对称位置都空)→ 结构对称,返回true; - 若一个节点为
NULL、另一个非NULL(对称位置一存一失)→ 结构不对称,返回false。
2. 值检查:若两个节点均存在,但值不相等 → 不对称,返回false。
3. 递归深入:当前节点检查通过后,递归检查「左节点的左 vs 右节点的右」和「左节点的右 vs 右节点的左」(需两者均对称,用 “与运算” 连接)。
(2)代码实现与详解
// 辅助函数:检查两个节点是否镜像对称
bool isMirror(TreeNode* leftNode, TreeNode* rightNode) {// 步骤1:边界条件(结构检查)// 情况1:两个节点都为空 → 对称if (leftNode == NULL && rightNode == NULL) {return true;}// 情况2:一个空、一个非空 → 不对称if (leftNode == NULL || rightNode == NULL) {return false;}// 步骤2:值检查(均非空时对比值)if (leftNode->val != rightNode->val) {return false;}// 步骤3:递归检查镜像位置(左左对右右,左右对右左)return isMirror(leftNode->left, rightNode->right) && isMirror(leftNode->right, rightNode->left);
}// 主函数:判断树是否轴对称
bool isSymmetric(TreeNode* root) {// 根节点为空(题目约束节点数≥1,此处兼容空树)if (root == NULL) {return true;}// 检查根节点的左子树与右子树是否镜像return isMirror(root->left, root->right);
}(3)关键细节
- 辅助函数的必要性:主函数无法直接处理 “对称位置” 的节点,需辅助函数接收两个节点(左子树和右子树的对应节点);
- 递归的镜像逻辑:比如示例 1 中,左子树的 2(根的左)与右子树的 2(根的右)对比后,需进一步检查 “左 2 的左(3)vs 右 2 的右(3)”“左 2 的右(4)vs 右 2 的左(4)”,完全匹配才对称;
3.3.2 方法二:迭代法(BFS / 队列实现)
(1)解题步骤
迭代的核心是 “同步处理对称节点对”:用队列存储「左子树的节点、右子树的对称节点」,每次取出一对节点检查,再将它们的 “镜像子节点” 成对入队,确保遍历顺序与镜像逻辑一致:
1. 初始化队列:将节点的左子树和右子树作为 “第一对对称节点” 入队;
2. 循环处理队列:
- 出队:取出队头的两个节点(
leftCurr为左子树节点,rightCurr为右子树的对称节点); - 检查:按 “边界条件→值” 的顺序判断,若不满足直接返回
false; - 入队:将
leftCurr的左、rightCurr的右(第一镜像对),leftCurr的右、rightCurr的左(第二镜像对)依次入队。
3. 队列遍历结束:所有对称节点对均检查通过,返回true。
(2)代码实现与详解(需队列辅助)
首先需要实现适配TreeNode*的队列(存储节点指针,每次处理一对节点):
// 队列节点结构(存储二叉树节点指针)
typedef struct QueueNode {TreeNode* data;struct QueueNode* next;
} QueueNode;// 队列结构(队头出、队尾入)
typedef struct Queue {QueueNode* front;QueueNode* rear;
} Queue;// 队列初始化:空队列,队头队尾均为NULL
void QueueInit(Queue* q) {q->front = q->rear = NULL;
}// 入队:从队尾添加元素
void QueuePush(Queue* q, TreeNode* val) {QueueNode* newNode = (QueueNode*)malloc(sizeof(QueueNode));newNode->data = val;newNode->next = NULL;if (q->rear == NULL) { // 空队列时,队头队尾指向新节点q->front = q->rear = newNode;} else { // 非空队列时,链接新节点并更新队尾q->rear->next = newNode;q->rear = newNode;}
}// 出队:从队头删除元素(需确保队列非空)
void QueuePop(Queue* q) {if (q->front == NULL) return;QueueNode* temp = q->front;q->front = q->front->next;if (q->front == NULL) { // 出队后为空,队尾置NULLq->rear = NULL;}free(temp); // 释放原队头内存
}// 判空:队列是否为空
bool QueueEmpty(Queue* q) {return q->front == NULL;
}// 获取队头元素(需确保队列非空)
TreeNode* QueueFront(Queue* q) {return q->front->data;
}// 销毁队列:释放所有队列节点内存
void QueueDestroy(Queue* q) {while (!QueueEmpty(q)) {QueuePop(q);}
}再实现核心的 “对称树判断” 逻辑:
bool isSymmetric(TreeNode* root) {if (root == NULL) {return true; // 兼容空树(题目约束节点数≥1,可省略)}// 步骤1:初始化队列,入队第一对对称节点(根的左、根的右)Queue q;QueueInit(&q);QueuePush(&q, root->left);QueuePush(&q, root->right);// 步骤2:循环处理队列中的对称节点对while (!QueueEmpty(&q)) {// 出队一对节点(leftCurr对应左子树,rightCurr对应右子树的对称位置)TreeNode* leftCurr = QueueFront(&q);QueuePop(&q);TreeNode* rightCurr = QueueFront(&q);QueuePop(&q);// 步骤3:结构检查(边界条件)if (leftCurr == NULL && rightCurr == NULL) {continue; // 均为空,无需后续检查,跳过当前轮}if (leftCurr == NULL || rightCurr == NULL) {QueueDestroy(&q); // 销毁队列避免内存泄漏return false; // 一存一失,不对称}// 步骤4:值检查(均非空时对比值)if (leftCurr->val != rightCurr->val) {QueueDestroy(&q);return false;}// 步骤5:入队下一对镜像节点(关键:确保对称顺序)QueuePush(&q, leftCurr->left); // 左的左QueuePush(&q, rightCurr->right); // 右的右(第一镜像对)QueuePush(&q, leftCurr->right); // 左的右QueuePush(&q, rightCurr->left); // 右的左(第二镜像对)}// 所有对称节点对均检查通过QueueDestroy(&q);return true;
}(3)关键细节
- 入队顺序的重要性:必须严格按 “左左→右右→左右→右左” 入队,确保下一轮处理的是 “对称位置” 的节点。若顺序错误(如左左→左右→右右→右左),会导致对比错位(如左左和左右对比,而非左左和右右);
- 空节点的处理:即使节点为空,若其对称位置有节点,也需入队检查;
- 内存安全:所有返回路径(包括
false)均需销毁队列,避免队列节点的内存泄漏。
四、另一棵树的子树
题目链接:https://leetcode.cn/problems/subtree-of-another-tree/description/
4.1 题目分析
题目要求:判断二叉树 root 中是否包含与 subRoot 结构完全一致、节点值完全相等的子树(子树定义:包含某个节点及其所有后代节点,root 也可视为自身的子树),是则返回true,否则返回false。
约束条件:
root节点数范围:[1, 2000],subRoot节点数范围:[1, 1000](均非空树,无需处理空树边界);- 节点值范围:
[-10⁴, 10⁴](支持负数对比)。
4.2 核心解题思路
“子树判断” 的本质是 “遍历 + 相同树校验” :
- 遍历主树
root:逐个访问root的每个节点,将每个节点视为 “潜在的子树根节点”; - 校验相同树:对每个 “潜在子树根节点”,调用 “相同树判断函数”(复用“相同的树”逻辑),检查以该节点为根的子树是否与
subRoot完全相同; - 结果判定:若存在任意一个 “潜在子树根节点” 通过校验,返回
true;遍历完root所有节点均未通过,返回false。
下面同样也介绍两种方法。
4.3 详细解题步骤与代码实现
4.3.1 核心辅助函数:判断两棵树是否相同(复用“相同的树”逻辑)
子树判断依赖 “相同树校验”,需先实现辅助函数 isSameTree,用于判断两棵树是否结构和值完全一致:
// 辅助函数:判断树a和树b是否完全相同(结构+值)
bool isSameTree(TreeNode* a, TreeNode* b) {// 边界1:两棵树当前节点均为空 → 相同if (a == NULL && b == NULL) {return true;}// 边界2:一棵空、一棵非空 → 不同if (a == NULL || b == NULL) {return false;}// 边界3:节点值不同 → 不同if (a->val != b->val) {return false;}// 递归校验左子树和右子树(需均相同)return isSameTree(a->left, b->left) && isSameTree(a->right, b->right);
}4.3.2 方法一:递归法
(1)解题步骤
递归遍历 root 的逻辑:
- 当前节点校验:判断以
root当前节点为根的子树是否与subRoot相同,若是则返回true; - 递归左子树:递归检查
root的左子树是否包含subRoot; - 递归右子树:递归检查
root的右子树是否包含subRoot; - 结果合并:左子树或右子树任意一个包含
subRoot,则返回true;否则返回false。
(2)代码实现与详解
bool isSubtree(TreeNode* root, TreeNode* subRoot) {// 边界:若root遍历到空(无更多节点可校验),返回falseif (root == NULL) {return false;}// 步骤1:校验当前节点为根的子树是否与subRoot相同if (isSameTree(root, subRoot)) {return true;}// 步骤2:递归校验左子树和右子树(只要一个包含就返回true)return isSubtree(root->left, subRoot) || isSubtree(root->right, subRoot);
}(3)关键细节
- 短路优化:若
root的左子树已找到匹配的子树,||运算符会直接返回true,无需再递归右子树,提升效率; - 遍历顺序:本质是
root的前序遍历(先校验当前节点,再遍历左右子树),确保每个节点都被作为 “潜在子树根” 检查。
4.3.3 方法二:迭代法(DFS / 栈实现)
(1)解题步骤
迭代遍历 root 的逻辑如下(用栈实现 DFS,模拟递归遍历顺序):
1. 初始化栈:将 root 入栈,栈存储 root 中待校验的 “潜在子树根节点”。
2. 循环处理栈:
- 出栈:取出栈顶节点(当前待校验的节点);
- 校验:调用
isSameTree检查该节点为根的子树是否与subRoot相同,若是则返回true; - 入栈:将该节点的右子树、左子树依次入栈(栈是 LIFO,先入右子树确保左子树先被处理,与递归顺序一致)。
3. 栈空返回:遍历完所有节点均未匹配,返回false。
(2)代码实现与详解(用栈辅助)
首先实现适配 TreeNode* 的栈结构:
// 栈节点结构(存储二叉树节点指针)
typedef struct StackNode {TreeNode* data;struct StackNode* next;
} StackNode;// 栈结构(栈顶入、栈顶出)
typedef struct Stack {StackNode* top; // 栈顶指针
} Stack;// 栈初始化:空栈,栈顶为NULL
void StackInit(Stack* s) {s->top = NULL;
}// 入栈:从栈顶添加元素
void StackPush(Stack* s, TreeNode* val) {StackNode* newNode = (StackNode*)malloc(sizeof(StackNode));newNode->data = val;newNode->next = s->top; // 新节点指向原栈顶s->top = newNode; // 更新栈顶为新节点
}// 出栈:从栈顶删除元素(需确保栈非空)
void StackPop(Stack* s) {if (s->top == NULL) return;StackNode* temp = s->top;s->top = s->top->next; // 栈顶后移free(temp); // 释放原栈顶内存
}// 判空:栈是否为空
bool StackEmpty(Stack* s) {return s->top == NULL;
}// 获取栈顶元素(需确保栈非空)
TreeNode* StackTop(Stack* s) {return s->top->data;
}// 销毁栈:释放所有栈节点内存
void StackDestroy(Stack* s) {while (!StackEmpty(s)) {StackPop(s);}
}再来实现核心的“子树判断” 逻辑:
bool isSubtree(TreeNode* root, TreeNode* subRoot) {// 步骤1:初始化栈,将root入栈(第一个待校验节点)Stack s;StackInit(&s);StackPush(&s, root);// 步骤2:循环处理栈中所有待校验节点while (!StackEmpty(&s)) {// 出栈:取出当前待校验节点TreeNode* curr = StackTop(&s);StackPop(&s);// 步骤3:校验当前节点为根的子树是否与subRoot相同if (isSameTree(curr, subRoot)) {StackDestroy(&s); // 销毁栈避免内存泄漏return true;}// 步骤4:将当前节点的右、左子树入栈(确保左子树先处理)if (curr->right != NULL) {StackPush(&s, curr->right);}if (curr->left != NULL) {StackPush(&s, curr->left);}}// 步骤5:遍历完所有节点均未匹配,销毁栈并返回falseStackDestroy(&s);return false;
}(3)关键细节
- 入栈顺序:先入右子树、再入左子树 —— 因栈是 “后进先出”(LIFO),左子树后入栈会先出栈,确保遍历顺序与递归法一致(左子树优先校验);
- 内存安全:所有返回路径(包括
true和false)均需调用StackDestroy释放栈节点内存,避免内存泄漏; - 空节点过滤:入栈前判断子树是否为空,避免空节点入栈(空节点不可能与非空的
subRoot匹配,减少无效校验)。
五、二叉树性质补充
💡二叉树性质
对于任何一棵二叉树,如果度为0其结点个数为,度为2的分支结点个数为
,则有
。
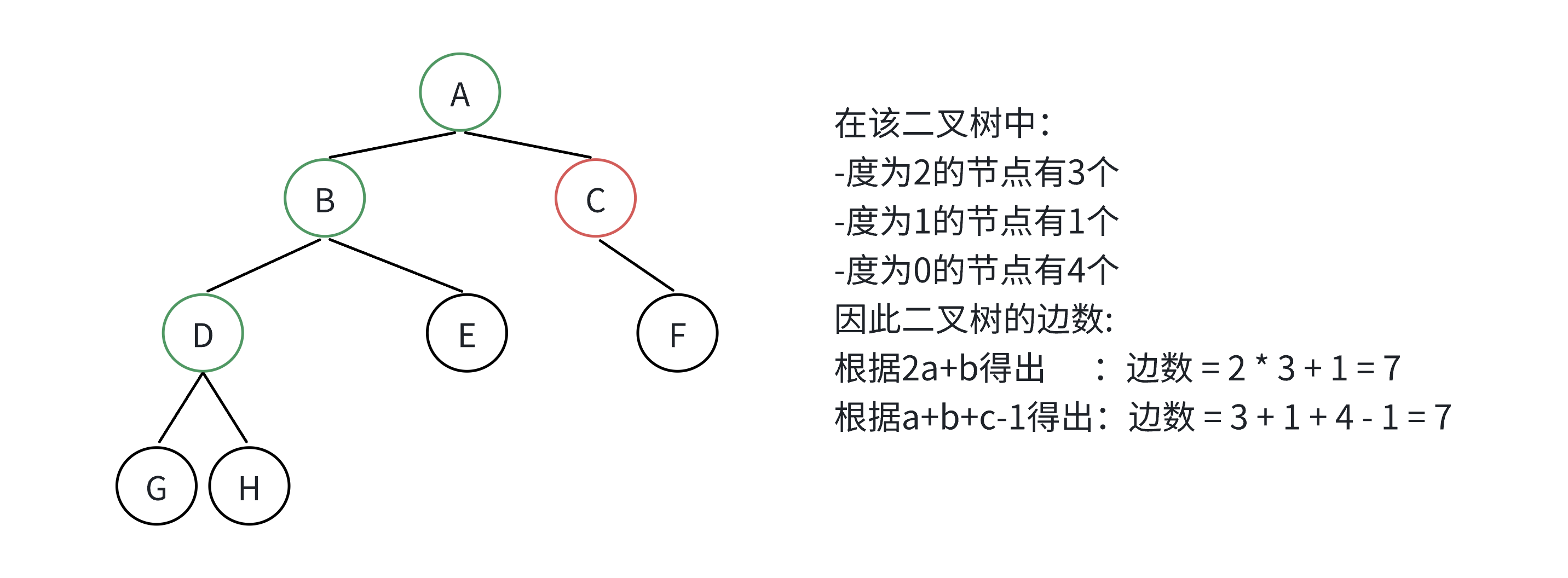
上述性质证明如下:
假设一个二叉树有a个度为2的结点,b个度为1的结点,c个叶子结点,则这个二叉树的边数就是;
另一方面,由于一共有个节点,所以边数又等于
。
结合上面两个公式可以得到:,即
。
总结
本期博客我为大家介绍了四道具有代表性的二叉树OJ题,并从不同角度为大家分析了解题思路。希望本期博客对大家学习二叉树能够有所帮助!感谢大家的支持!!!
