当前位置： 首页 > news >正文

ego(5)---Astar绕障

news 2025/9/16 13:13:52

Astar的基础原理

关于 Astar 算法的原理网上有特别多，因为也不算是特别难推导的，我之前也有文章专门介绍 Astar 的算法：https://blog.csdn.net/a_xiaoning/article/details/123518943?spm=1001.2014.3001.5501
因此，这里就简单回顾一下 Astar 的一些基础概念，然后再分析 ego 工程。
Astar 的核心公式是：
f(n) = g(n) + h(n)
用以评估每个节点的代价，其中：
  1. g(n) 表示从起点到当前节点 n 的实际代价(已走距离，耗时等)
  2. h(n) 表示从当前节点 n 到终点的估计代价(如欧式距离，曼哈顿距离或其他启发函数)
算法总是优先处理总代价最小的节点，这样就可以大致以最优路径来快速收敛到终点。

ego中的Astar应用

开集与闭集

在 ego 中使用开集与闭集的概念，区分节点的状态。
  1. 开集(OPENSET) 存放已发现但还未处理的节点，也就是邻居还没有探索完的点，每次在开集中取代价最小的节点进一步探索
  2. 闭集(CLOSESET) 存放已处理完毕的节点，也就是已探索完所有邻居的节点，确保不会重复处理，减少无效计算。

ego 中的搜索流程

Astar 在 ego 中是使用在上一节检测到B样条轨迹中的障碍物进出点后，其流程大致如下：
  1. 初始化：将起点加入开集，g = 0， h 按启发函数计算：
// 初始化起始节点
startPtr->index = start_idx;
startPtr->rounds = rounds_; // 标记当前轮回次数
startPtr->gScore = 0;   // 存储节点到起始点的代价 g 
startPtr->fScore = getHeu(startPtr, endPtr);    // f = g + 启发值h
startPtr->state = GridNode::OPENSET; //put start node in open set   路径集中加入起始点
startPtr->cameFrom = NULL;  // 起始点的父节点设置为空
openSet_.push(startPtr); //put start in open set   Astar路径集中添加初始点
  1. 循环执行：在开集中取代价最小的节点记作 current，检测 current 是否是终点，如果是终点，则回溯路径并记录(因为一直会记录节点的父节点，因此从终点一直往前找父节点，就能找到完整路径)，如果不是终点，则探索当前节点的所有邻居节点；
  2. 探索邻居节点：对 current 的所有相邻节点，计算其 g 值(从起点到当前节点的距离)，若邻居未在开集或闭集中，或者找到更优的 g 值，则更新其 g 与 f ，加入开集；
  3. 标记：将处理完的 current 移入闭集，重复 2-3 步骤，直到开集为空(开集为空表示无路径)，或找到终点。
对应 ego 中的代码如下(加入了部分注释)：
    int num_iter = 0;while (!openSet_.empty()){num_iter++;current = openSet_.top();   // 取出代价最小的节点openSet_.pop();// if ( num_iter < 10000 )//     cout << "current=" << current->index.transpose() << endl;// 检测是否到达目标点if (current->index(0) == endPtr->index(0) && current->index(1) == endPtr->index(1) && current->index(2) == endPtr->index(2)){// ros::Time time_2 = ros::Time::now();// printf("\033[34mA star iter:%d, time:%.3f\033[0m\n",num_iter, (time_2 - time_1).toSec()*1000);// if((time_2 - time_1).toSec() > 0.1)//     ROS_WARN("Time consume in A star path finding is %f", (time_2 - time_1).toSec() );gridPath_ = retrievePath(current);  // 回溯路径return true;}current->state = GridNode::CLOSEDSET; //move current node from open set to closed set.   CLOSEDSET 表示已探索过/******************搜索邻居节点*******************/ // 在三维空间中，每个节点有26个可能的邻居(xyz三轴分别±1，9+9+8)for (int dx = -1; dx <= 1; dx++)for (int dy = -1; dy <= 1; dy++)for (int dz = -1; dz <= 1; dz++){if (dx == 0 && dy == 0 && dz == 0)continue;   // 跳过自身// 计算当前邻居节点的索引Vector3i neighborIdx;neighborIdx(0) = (current->index)(0) + dx;neighborIdx(1) = (current->index)(1) + dy;neighborIdx(2) = (current->index)(2) + dz;// 检查邻居是否在有效范围内if (neighborIdx(0) < 1 || neighborIdx(0) >= POOL_SIZE_(0) - 1 || neighborIdx(1) < 1 || neighborIdx(1) >= POOL_SIZE_(1) - 1 || neighborIdx(2) < 1 || neighborIdx(2) >= POOL_SIZE_(2) - 1){continue;}// 获取邻居节点指针neighborPtr = GridNodeMap_[neighborIdx(0)][neighborIdx(1)][neighborIdx(2)];neighborPtr->index = neighborIdx;bool flag_explored = neighborPtr->rounds == rounds_;    // 是否为本轮已探索的节点// 如果已经标记为探索过，则跳过if (flag_explored && neighborPtr->state == GridNode::CLOSEDSET){continue; //in closed set.}neighborPtr->rounds = rounds_;// 检查邻居节点是否为障碍物，是则跳过if (checkOccupancy(Index2Coord(neighborPtr->index))){continue;}// 计算到达邻居节点的代价(使用欧氏距离)double static_cost = sqrt(dx * dx + dy * dy + dz * dz);tentative_gScore = current->gScore + static_cost;// 如果是未探索节点，则将节点加入开集(未探索点的集合)，并设置初始代价if (!flag_explored){//discover a new nodeneighborPtr->state = GridNode::OPENSET;neighborPtr->cameFrom = current;neighborPtr->gScore = tentative_gScore;neighborPtr->fScore = tentative_gScore + getHeu(neighborPtr, endPtr);openSet_.push(neighborPtr); //put neighbor in open set and record it.}// 如果是已探索节点但发现更优路径else if (tentative_gScore < neighborPtr->gScore){ //in open set and need updateneighborPtr->cameFrom = current;neighborPtr->gScore = tentative_gScore;neighborPtr->fScore = tentative_gScore + getHeu(neighborPtr, endPtr);}}ros::Time time_2 = ros::Time::now();// 超时判断if ((time_2 - time_1).toSec() > 0.2){ROS_WARN("Failed in A star path searching !!! 0.2 seconds time limit exceeded.");return false;}}

ego中的启发函数

启发函数的作用是用来计算当前节点到终点的代价，在 ego 中，使用量节点的标号差，再结合三维，二维，平面距离来计算。假设体素边长为1，那么一个体素差的平面距离就是1，二维距离就是 sqrt(2)，三维距离就是 sqrt(3)：

double AStar::getDiagHeu(GridNodePtr node1, GridNodePtr node2)
{// 计算三维坐标差(两个节点在 xyz 三轴上的标号差值)double dx = abs(node1->index(0) - node2->index(0));double dy = abs(node1->index(1) - node2->index(1));double dz = abs(node1->index(2) - node2->index(2));double h = 0.0;int diag = min(min(dx, dy), dz);    // 确定三个方向中的最小差值// 减去最短的一维差值，则剩余两维较长的距离dx -= diag;dy -= diag;dz -= diag;// 总的代价按标号差的三维，二维，一维距离计算，边长为1时，三维对角线距离为 sqrt(3)，二维对角线距离为 sqrt(2)，平面距离为 1if (dx == 0){h = 1.0 * sqrt(3.0) * diag + sqrt(2.0) * min(dy, dz) + 1.0 * abs(dy - dz);}if (dy == 0){h = 1.0 * sqrt(3.0) * diag + sqrt(2.0) * min(dx, dz) + 1.0 * abs(dx - dz);}if (dz == 0){h = 1.0 * sqrt(3.0) * diag + sqrt(2.0) * min(dx, dy) + 1.0 * abs(dx - dy);}return h;
}

python验证

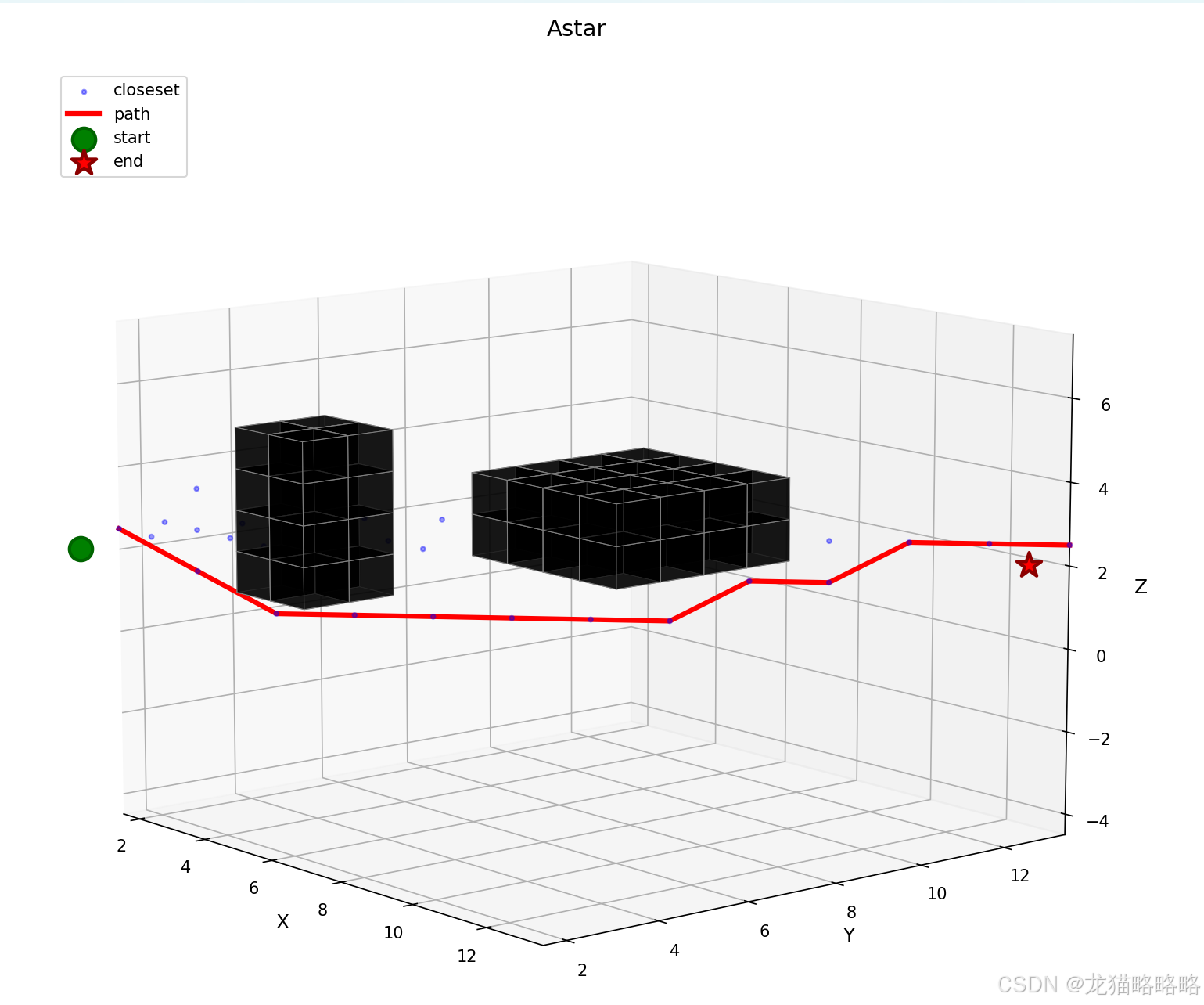
根据 ego 的主要思想，编写了一段大概的 python 验证代码来看一下效果：

import math
import heapq
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
from mpl_toolkits.mplot3d.art3d import Poly3DCollectionclass GridNode:"""网格节点类，存储A*算法所需的节点信息"""def __init__(self, index):self.index = np.array(index, dtype=int)  # 三维索引 (x, y, z)self.rounds = -1  # 所属搜索轮次self.g_score = float('inf')  # 从起点到当前节点的实际代价self.f_score = float('inf')  # 估计总代价 = g_score + h_scoreself.state = 0  # 0: 未探索, 1: 开放集, 2: 关闭集self.came_from = None  # 路径回溯指针def __repr__(self):return f"GridNode(index={self.index}, g={self.g_score:.2f}, f={self.f_score:.2f})"class AStar:"""三维A*路径搜索算法类（XYZ轴刻度等长）"""def __init__(self, grid_size, resolution=1.0):"""初始化A*算法:param grid_size: 三维网格大小 (x_size, y_size, z_size):param resolution: 网格分辨率（每个网格的实际尺寸）"""self.grid_size = np.array(grid_size, dtype=int)self.resolution = resolutionself.inv_resolution = 1.0 / resolution# 初始化三维网格节点地图self.grid_node_map = self._initialize_grid()self.open_set = []  # 开放集，使用优先队列实现self.rounds = 0  # 搜索轮次计数器self.grid_path = []  # 存储找到的路径self.explored_nodes = []  # 存储探索过的节点，用于可视化# 定义26个邻居方向（三维空间）self.neighbor_directions = [np.array([dx, dy, dz])for dx in [-1, 0, 1]for dy in [-1, 0, 1]for dz in [-1, 0, 1]if not (dx == 0 and dy == 0 and dz == 0)]def _initialize_grid(self):"""初始化三维网格节点地图"""grid = []for x in range(self.grid_size[0]):y_grid = []for y in range(self.grid_size[1]):z_grid = [GridNode([x, y, z]) for z in range(self.grid_size[2])]y_grid.append(z_grid)grid.append(y_grid)return griddef coord_to_index(self, coord):"""将三维坐标转换为网格索引"""index = np.round(coord * self.inv_resolution).astype(int)index = np.clip(index, [0, 0, 0], self.grid_size - 1)  # 确保索引有效return indexdef index_to_coord(self, index):"""将网格索引转换为三维坐标（返回网格中心坐标）"""return (index + 0.5) * self.resolution  # +0.5确保坐标在网格中心def check_occupancy(self, coord, obstacle_map):"""检查坐标点是否为障碍物"""index = self.coord_to_index(coord)if np.any(index < 0) or np.any(index >= self.grid_size):return True  # 超出网格范围视为障碍物return obstacle_map[index[0], index[1], index[2]] == 1def get_heu(self, node1, node2):"""计算启发值，使用对角线启发式函数"""dx = abs(node1.index[0] - node2.index[0])dy = abs(node1.index[1] - node2.index[1])dz = abs(node1.index[2] - node2.index[2])h = 0.0diag = min(min(dx, dy), dz)dx -= diagdy -= diagdz -= diag# 三维对角线、二维对角线、直线移动的代价加权if dx == 0:h = math.sqrt(3) * diag + math.sqrt(2) * min(dy, dz) + 1.0 * abs(dy - dz)if dy == 0:h = math.sqrt(3) * diag + math.sqrt(2) * min(dx, dz) + 1.0 * abs(dx - dz)if dz == 0:h = math.sqrt(3) * diag + math.sqrt(2) * min(dx, dy) + 1.0 * abs(dx - dy)return h * self.resolution  # 转换为实际距离def retrieve_path(self, current_node):"""从终点回溯到起点，获取路径"""path = []current = current_nodewhile current is not None:coord = self.index_to_coord(current.index)path.append(coord)current = current.came_fromreturn path[::-1]  # 反转路径为“起点→终点”顺序def astar_search(self, start_coord, end_coord, obstacle_map, max_time=0.2):"""执行A*路径搜索"""import timestart_time = time.time()self.rounds += 1self.explored_nodes = []  # 重置探索节点记录# 坐标转索引并检查起点/终点合法性start_index = self.coord_to_index(start_coord)end_index = self.coord_to_index(end_coord)if self.check_occupancy(start_coord, obstacle_map) or self.check_occupancy(end_coord, obstacle_map):print("起点或终点在障碍物中，无法搜索路径")return False, []# 初始化起点节点start_node = self.grid_node_map[start_index[0]][start_index[1]][start_index[2]]end_node = self.grid_node_map[end_index[0]][end_index[1]][end_index[2]]start_node.rounds = self.roundsstart_node.g_score = 0.0start_node.f_score = self.get_heu(start_node, end_node)start_node.state = 1  # 标记为开放集start_node.came_from = None# 清空开放集并加入起点（用id避免节点比较冲突）self.open_set = []heapq.heappush(self.open_set, (start_node.f_score, id(start_node), start_node))num_iter = 0found = Falsewhile self.open_set:# 超时判断if time.time() - start_time > max_time:print(f"A*搜索超时（超过{max_time}秒）")return False, []num_iter += 1_, _, current_node = heapq.heappop(self.open_set)self.explored_nodes.append(current_node)  # 记录探索节点# 到达终点：回溯路径if np.array_equal(current_node.index, end_node.index):self.grid_path = self.retrieve_path(current_node)found = Truebreakcurrent_node.state = 2  # 标记为关闭集# 探索26个邻居for dir in self.neighbor_directions:neighbor_index = current_node.index + dir# 检查邻居索引有效性if np.any(neighbor_index < 0) or np.any(neighbor_index >= self.grid_size):continueneighbor_node = self.grid_node_map[neighbor_index[0]][neighbor_index[1]][neighbor_index[2]]is_explored = (neighbor_node.rounds == self.rounds)# 跳过关闭集节点if is_explored and neighbor_node.state == 2:continueneighbor_node.rounds = self.rounds  # 标记为本轮次# 跳过障碍物neighbor_coord = self.index_to_coord(neighbor_index)if self.check_occupancy(neighbor_coord, obstacle_map):continue# 计算代价并更新节点step_cost = np.linalg.norm(dir) * self.resolution  # 欧氏距离代价tentative_g_score = current_node.g_score + step_costif not is_explored or tentative_g_score < neighbor_node.g_score:neighbor_node.came_from = current_nodeneighbor_node.g_score = tentative_g_scoreneighbor_node.f_score = tentative_g_score + self.get_heu(neighbor_node, end_node)if not is_explored:neighbor_node.state = 1heapq.heappush(self.open_set, (neighbor_node.f_score, id(neighbor_node), neighbor_node))print(f"A*搜索完成：迭代{num_iter}次，耗时{time.time() - start_time:.4f}秒")return found, self.grid_path if found else []def _get_cube_faces(self, center_coord, size):"""生成立方体的6个面（用于绘制障碍物立体块）"""x, y, z = center_coordhalf_size = size / 2.0# 立方体8个顶点（x±half, y±half, z±half）vertices = [[x - half_size, y - half_size, z - half_size],[x + half_size, y - half_size, z - half_size],[x + half_size, y + half_size, z - half_size],[x - half_size, y + half_size, z - half_size],[x - half_size, y - half_size, z + half_size],[x + half_size, y - half_size, z + half_size],[x + half_size, y + half_size, z + half_size],[x - half_size, y + half_size, z + half_size]]# 6个面的顶点索引（每个面4个顶点）faces = [[0, 1, 2, 3],  # 底面（z-）[4, 5, 6, 7],  # 顶面（z+）[0, 1, 5, 4],  # 前面（y-）[2, 3, 7, 6],  # 后面（y+）[0, 3, 7, 4],  # 左面（x-）[1, 2, 6, 5]  # 右面（x+）]# 转换为面的顶点坐标列表face_coords = [[vertices[i] for i in face] for face in faces]return face_coordsdef plot_3d_scene(self, start_coord, end_coord, obstacle_map):"""绘制3D场景：XYZ轴刻度等长"""if not self.grid_path:print("无路径可绘制（未找到有效路径）")return# 创建3D图fig = plt.figure(figsize=(12, 10))ax = fig.add_subplot(111, projection='3d')# 1. 绘制障碍物（黑色立体块）obstacle_faces = []for x in range(self.grid_size[0]):for y in range(self.grid_size[1]):for z in range(self.grid_size[2]):if obstacle_map[x, y, z] == 1:# 获取障碍物网格中心坐标obs_center = self.index_to_coord(np.array([x, y, z]))# 生成立方体6个面cube_faces = self._get_cube_faces(obs_center, self.resolution)obstacle_faces.extend(cube_faces)# 批量添加障碍物面（黑色半透明，有边框）if obstacle_faces:obs_collection = Poly3DCollection(obstacle_faces,facecolors='black',  # 面颜色：黑色edgecolors='gray',  # 边框颜色：灰色alpha=0.7,  # 透明度：70%linewidths=0.5  # 边框宽度)ax.add_collection3d(obs_collection)# 2. 绘制探索过的节点（蓝色小点，半透明）if self.explored_nodes:explored_coords = np.array([self.index_to_coord(node.index) for node in self.explored_nodes])ax.scatter(explored_coords[:, 0], explored_coords[:, 1], explored_coords[:, 2],c='blue', marker='.', s=30, alpha=0.4, label='closeset')# 3. 绘制路径（红色实线，加粗）path_coords = np.array(self.grid_path)ax.plot(path_coords[:, 0], path_coords[:, 1], path_coords[:, 2],'r-', linewidth=3, label='path')# 4. 标记起点（绿色大圆点）和终点（红色大星号）ax.scatter(start_coord[0], start_coord[1], start_coord[2],c='green', marker='o', s=200, edgecolors='darkgreen', linewidths=2, label='start')ax.scatter(end_coord[0], end_coord[1], end_coord[2],c='red', marker='*', s=250, edgecolors='darkred', linewidths=2, label='end')# 图轴与标题设置ax.set_xlabel('X', fontsize=12)ax.set_ylabel('Y', fontsize=12)ax.set_zlabel('Z', fontsize=12)ax.set_title('Astar', fontsize=14, pad=20)ax.legend(fontsize=10, loc='upper left')ax.grid(True, alpha=0.3)# 关键修改：设置XYZ轴等长刻度# 获取数据的最大范围max_range = np.array([path_coords[:, 0].max() - path_coords[:, 0].min(),path_coords[:, 1].max() - path_coords[:, 1].min(),path_coords[:, 2].max() - path_coords[:, 2].min()]).max() / 2.0# 获取数据中心mid_x = (path_coords[:, 0].max() + path_coords[:, 0].min()) * 0.5mid_y = (path_coords[:, 1].max() + path_coords[:, 1].min()) * 0.5mid_z = (path_coords[:, 2].max() + path_coords[:, 2].min()) * 0.5# 设置XYZ轴范围相同，确保刻度线长度一致ax.set_xlim(mid_x - max_range, mid_x + max_range)ax.set_ylim(mid_y - max_range, mid_y + max_range)ax.set_zlim(mid_z - max_range, mid_z + max_range)# 调整视角ax.view_init(elev=30, azim=45)plt.tight_layout()return fig# 仿真测试：生成简洁的障碍物场景并绘制3D结果
def simulate_3d_astar():# 1. 配置网格与障碍物（减少障碍物数量）grid_size = (15, 15, 5)  # 15x15x5的三维网格resolution = 1.0  # 每个网格1m×1m×1mastar = AStar(grid_size, resolution)# 创建障碍物地图（1表示障碍物，0表示自由空间）obstacle_map = np.zeros(grid_size, dtype=int)# 障碍物1：中间的一个小型立方体（x6-9, y6-9, z2-3）obstacle_map[6:10, 6:10, 2:4] = 1# 障碍物2：一个垂直小柱子（x3-4, y3-4, z1-4）obstacle_map[3:5, 3:5, 1:5] = 1# 2. 配置起点与终点start_coord = np.array([1.0, 1.0, 2.0])  # 左下角起点end_coord = np.array([13.0, 13.0, 2.0])  # 右上角终点# 3. 执行A*搜索并绘制3D场景found, path = astar.astar_search(start_coord, end_coord, obstacle_map)if found:print(f"找到有效路径，共{len(path)}个路径点")fig = astar.plot_3d_scene(start_coord, end_coord, obstacle_map)plt.show()else:print("未找到从起点到终点的路径")if __name__ == "__main__":simulate_3d_astar()


文章转载自：

http://V9UG2u8m.czxrg.cn
http://GLLNNdg3.czxrg.cn
http://x7FhHEBT.czxrg.cn
http://WWPiuth2.czxrg.cn
http://YQGjDUYB.czxrg.cn
http://w8dwkvxE.czxrg.cn
http://UtipO9eC.czxrg.cn
http://dpuQprXn.czxrg.cn
http://vNFB9Syw.czxrg.cn
http://HKNruzQn.czxrg.cn
http://jtHWBE4L.czxrg.cn
http://h0sFe746.czxrg.cn
http://ngxnwHRC.czxrg.cn
http://onpA5rwl.czxrg.cn
http://C7kXNnwZ.czxrg.cn
http://sUab6545.czxrg.cn
http://6kuFbWHB.czxrg.cn
http://Qf0FaoTG.czxrg.cn
http://DZfgXydW.czxrg.cn
http://sJVM2h9S.czxrg.cn
http://imLcy6Rb.czxrg.cn
http://lOTozf7g.czxrg.cn
http://L3H0ekkv.czxrg.cn
http://ApKdvj1C.czxrg.cn
http://zvzKfw2B.czxrg.cn
http://8ltGgKVm.czxrg.cn
http://Nyi3IEIO.czxrg.cn
http://xlnGyjyp.czxrg.cn
http://dcrhA7S3.czxrg.cn
http://YDB6U8en.czxrg.cn
http://www.dtcms.com/a/385539.html

相关文章：

  • UE5C++编译遇到MSB3073
  • 记一次JS逆向学习
  • 【PyTorch】单目标检测
  • RabbitMQ—基础篇
  • 介绍一下 Test-Time Training 技术
  • 【LangChain指南】Document loaders
  • 日语学习-日语知识点小记-进阶-JLPT-N1阶段蓝宝书，共120语法（10）：9１-100语法＋考え方１３
  • 2021/07 JLPT听力原文 问题四
  • MySQL 视图的更新与删除：从操作规范到风险防控
  • 【SQLMap】获取 Shell
  • Java之异常处理
  • C# 通过 TCP/IP 控制 Keysight 34465A 万用表（保姆级教程）
  • TVS二极管详解：原理、选型与应用实战
  • C++实现文件中单词统计等
  • 数据库（四）MySQL读写分离原理和实现
  • 关于数据库的导入和导出
  • 【氮化镓】GaN中受主的氢相关钝化余激活
  • AI 进课堂 - 语文教学流程重塑
  • 最近一些机器github解析到本地回环地址127.0.0.1
  • P6352 [COCI 2007/2008 #3] CETIRI
  • 【LeetCode 每日一题】37. 解数独
  • 多项式回归：线性回归的扩展
  • AI生成到无缝PBR材质：Firefly+第三方AI+Substance工作流
  • Java分布式锁实战指南：从理论到实践
  • 【CSS】层叠上下文和z-index
  • inline-block元素错位原因及解决方法
  • 【Java】P3 Java基础：关键字、标识符与变量详解
  • Golang语言入门篇003_Go源代码结构
  • 【Docker】报错Data page checksums are disabled.
  • Viper：Go语言中强大的配置管理库入门教程