LeetCode热题100--105. 从前序与中序遍历序列构造二叉树--中等
1. 题目
给定两个整数数组 preorder 和 inorder ,其中 preorder 是二叉树的先序遍历, inorder 是同一棵树的中序遍历,请构造二叉树并返回其根节点。
示例 1:
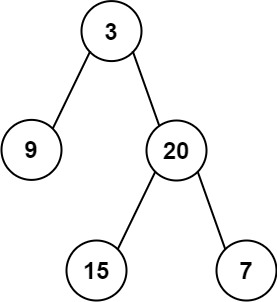
输入: preorder = [3,9,20,15,7], inorder = [9,3,15,20,7]
输出: [3,9,20,null,null,15,7]
示例 2:
输入: preorder = [-1], inorder = [-1]
输出: [-1]
2. 题解
/*** Definition for a binary tree node.* public class TreeNode {* int val;* TreeNode left;* TreeNode right;* TreeNode() {}* TreeNode(int val) { this.val = val; }* TreeNode(int val, TreeNode left, TreeNode right) {* this.val = val;* this.left = left;* this.right = right;* }* }*/
class Solution {int[] preorder;HashMap<Integer, Integer> dic = new HashMap<>();public TreeNode buildTree(int[] preorder, int[] inorder) {this.preorder = preorder;for(int i = 0; i < inorder.length; i++)dic.put(inorder[i], i);return recur(0, 0, inorder.length - 1);}TreeNode recur(int root, int left, int right) {if (left > right) return null; // 递归终止TreeNode node = new TreeNode(preorder[root]); // 建立根节点int i = dic.get(preorder[root]); // 划分根节点、左子树、右子树node.left = recur(root + 1, left, i - 1); // 开启左子树递归node.right = recur(root + i - left + 1, i + 1, right); // 开启右子树递归return node; // 回溯返回根节点}
}
3. 题解
出自:105. 从前序与中序遍历序列构造二叉树(分治,清晰图解)
1-6行:这是对TreeNode类的定义或者说结构体的定义,它是一棵二叉树,其中每个节点最多有两个子节点,一个左子节点和一个右子节点。如果没有提供值、左子节点或右子节点,它们将默认为null。
8-10行:这些代码定义了一个名为Solution的类,其中包含了一些与二叉树相关的方法。这段代码的主要功能是根据前序遍历和中序遍历结果来构建二叉树。
9行:将输入的前序遍历数组赋值给成员变量preorder。
11-12行:创建一个HashMap dic,用于存储中序遍历的元素及其在中序遍历中的索引。这样可以根据中序遍历结果定位根节点和左右子树的位置。
14行:调用recur函数构建二叉树。传入参数0表示前序遍历的第一个元素作为根节点,0和inorder.length - 1分别表示左边界和右边界,用于划分中序遍历结果。
23-44行:这是一个递归函数,用于根据前序遍历结果构建二叉树。该函数接受三个参数:root、left和right,分别代表前序遍历的根节点索引、中序遍历的左边界和右边界。
- 如果左边界大于右边界,表示无法继续划分子树,返回null。
- 否则,创建一个新的TreeNode,值为preorder[root](即前序遍历的根节点)。
- 在HashMap dic中查找根节点的索引i,并将其设为左子树和右子树的中界。然后递归构建左右子树。
- 最后返回当前处理的TreeNode。
在这段代码中,我们使用了前序遍历和中序遍历来确定二叉树的结构。在每一步中,我们根据前序遍历结果找到根节点,然后在中序遍历结果中划分出左子树和右子树,并递归构建它们。这样就可以从给定的前序遍历和中序遍历结果重建一棵二叉树。
