当前位置：首页 > news >正文

扩散模型之（五）基于概率流ODE方法

news 2025/9/15 10:37:20

1. 概述

本文分析SDE方法的一个特例即去除随机项得到的ODE方法。

2. SDE回顾

$\begin{aligned} \frac{\mathrm{d} \mathbf{x}_{t}}{\mathrm{d} t} = \left( f(\mathbf{x}_{t}, t) - \frac{1}{2}g^{2}(t) \nabla_{\mathbf{x}_{t}} \ln p_{t}(\mathbf{x}_{t}) \right) . \end{aligned}$

$\begin{aligned} \mathcal{L}(\theta) = \int_{0}^{1} \mathcal{L}_t(\theta) \mathrm{d} t . \end{aligned}$

$\Large \begin{aligned} \mathcal{L}_t(\theta) = \frac{1}{2} \mathbb{E}_{\mathbf{x}_0 \sim p_{data}(\mathbf{x})} \mathbb{E}_{\mathbf{x}_t \sim p_{0t}(\mathbf{x}_t|\mathbf{x}_0)} \left[ \lambda_t \| s_{\theta}(\mathbf{x}_t, t) - \nabla_{\mathbf{x}_t} \ln p_{0t}(\mathbf{x}_t|\mathbf{x}_0) \|^2 \right] . \end{aligned}$

$\Large \begin{aligned} \mathbf{x}_{t} = \mathbf{x}_{t+\Delta} - \left( f(\mathbf{x}_{t+\Delta}, t+\Delta) - \frac{1}{2}g^{2}(t+\Delta) \nabla_{\mathbf{x}_{t+\Delta}} \ln p_{t}(\mathbf{x}_{t+\Delta}) \right) \cdot \Delta . \end{aligned}$

需注意：这里假定漂移项和扩散项均为已知条件。虽然我们坚持使用（后向）欧拉方法，但完全可以选用其他ODE求解器。不过本文为保证清晰性和简洁性，将采用最基础的方法。

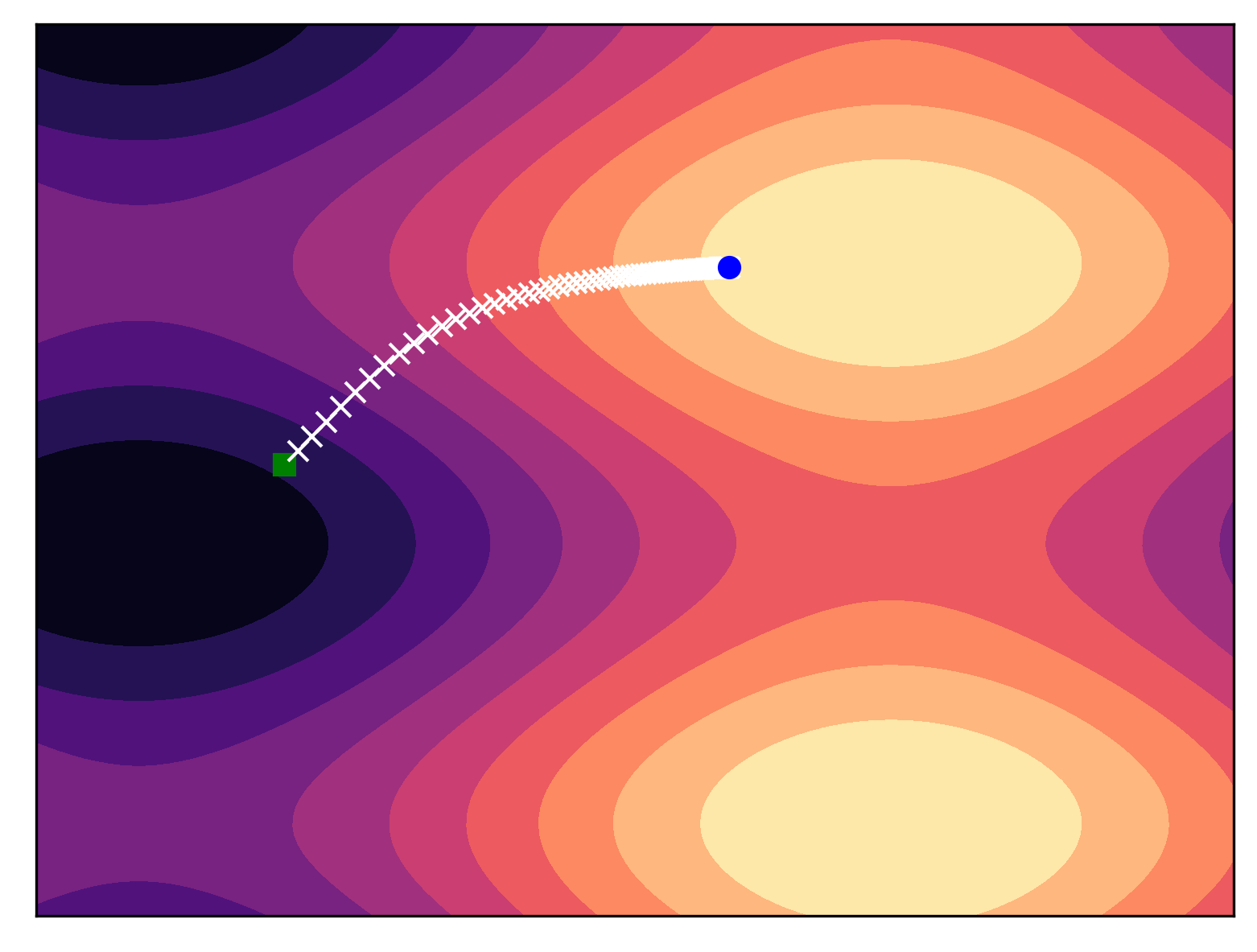
图1展示了使用后向欧拉方法进行采样的示例。对于某个概率流ODE（PF-ODE）和给定的评分函数，我们可以从多峰分布中获取样本。可以想象，ODE求解器会"朝向"分布模态移动。通过这个简单示例可以看出，定义概率流ODE实为一种强大的生成工具。只要评分函数得到恰当近似，我们便能以直接的方式从原始分布中进行采样。

3.方差爆炸PF-ODE

在（Song等人，2020）和（Song等人，2021）的研究中，我们可以找到三类随机梯度生成模型（SGBMs）的典型示例：方差爆炸（VE）型随机微分方程、方差保持（VP）型随机微分方程以及次方差保持（sub-VP）型随机微分方程。本文将重点探讨方差爆炸型随机微分方程（VE SDE）。

在VE-SDE中，考虑选择如下的漂移项与扩散项：

$f(\mathbf{x}, t) = 0$
$g(t) = \sigma^{t}$ ，其中 $\sigma > 0$ 为超参数，

根据上述的分析，选取适当的 $f(\mathbf{x}, t)$ 与 $g(t)$ 得到通用形式的PF-ODE方程如下：

$\Large\begin{aligned} \frac{\mathrm{d} \mathbf{x}_{t}}{\mathrm{d} t} = - \frac{1}{2} \sigma^{2t} \nabla_{\mathbf{x}_t} \ln p_{t}(\mathbf{x}_{t}) \end{aligned}$

现在为了训练评分模型，我们需要定义用于获取 $\mathbf{x}_0$ 加噪版本的条件分布。幸运的是，随机微分方程理论（参见Särkkä与Solin2019年著作第五章）揭示了如何计算 $p_{0t}(\mathbf{x}_{t}|\mathbf{x}_0)$ 具体计算公式已发表于（Song等人，2020）的附录中。此处我们直接给出最终解：

$\Large \begin{aligned} p_{0t}(\mathbf{x}_{t}|\mathbf{x}_0) = \mathcal{N}\left(\mathbf{x}_t | \mathbf{x}_0, \frac{1}{2 \ln \sigma}(\sigma^{2t} - 1) \mathbf{I}\right) \end{aligned}$

因此得到随时间变化的方差的函数形式如下：

$\Large \begin{aligned} \sigma_t^2 = \frac{1}{2 \ln \sigma}(\sigma^{2t} - 1) \end{aligned}$

最终得到的 $p_{01}(\mathbf{x})$ 为如下的近似高斯分布：

$\begin{aligned} p_{01}(\mathbf{x}) &= \int p_{0}(\mathbf{x}_0) * \mathcal{N} \left( \mathbf{x} | \mathbf{x}_{0}, \frac{1}{2 \ln \sigma}(\sigma^{2} - 1)\mathbf{I} \right) \\ &\approx \mathcal{N}\left( \mathbf{x} | 0, \frac{1}{2 \ln \sigma}(\sigma^{2} - 1)\mathbf{I} \right) . \end{aligned}$