深度学习(九):逻辑回归
逻辑回归(Logistic Regression)是机器学习与深度学习中最经典、最基础的模型之一。虽然名字里带有“回归”,但它实际上是一个用于分类问题的线性模型,通常用于二分类任务。
基本概念
逻辑回归是一种广义线性模型(GLM),它通过对输入特征进行线性组合,然后使用逻辑函数(sigmoid)将结果映射到 [0,1] 区间,输出可以看作是样本属于某一类别的概率。
-
输入:样本特征向量 x∈Rn
-
参数:权重向量 w、偏置项 b
-
线性变换:
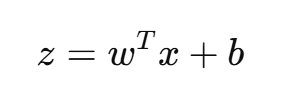
-
非线性映射(sigmoid):
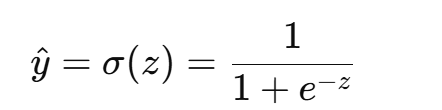
-
输出:y^∈(0,1),代表样本属于正类(y=1)的概率。
因此,逻辑回归的决策边界由线性函数决定,而概率估计则通过 sigmoid 完成。
逻辑回归的数学推导
概率建模
在二分类问题中,设样本的真实标签 y∈{0,1},预测概率为:
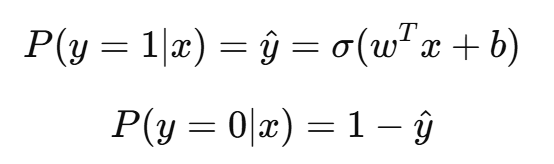
即模型对样本属于正类/负类的概率进行建模。
损失函数
逻辑回归采用极大似然估计(MLE)来求解参数。假设训练集有 m 个样本:
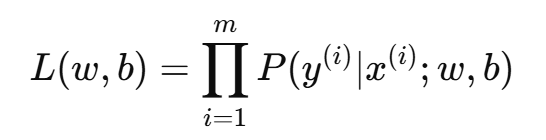
取对数似然函数:
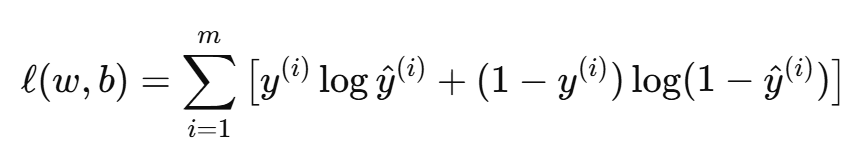
为了最小化损失,通常定义负对数似然作为损失函数:
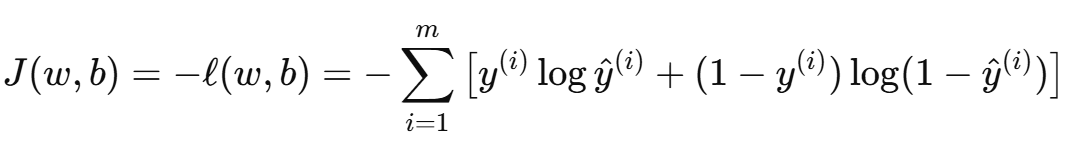
这就是著名的 交叉熵损失(Cross Entropy Loss)。
梯度下降更新
对参数求梯度:
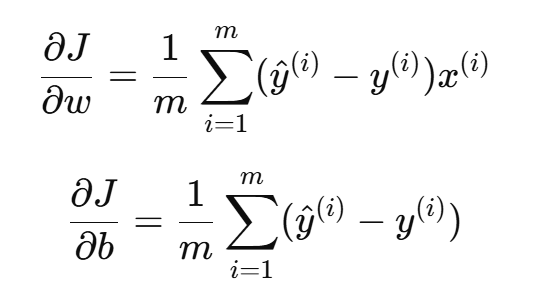
采用梯度下降法更新参数:
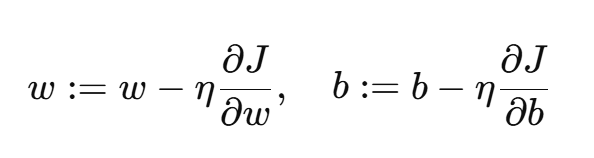
其中 η 是学习率。
逻辑回归与深度学习的关系
单层神经网络
- 逻辑回归可以看作是一个只有输入层和输出层的神经网络:
- 输入层:特征向量 x
- 权重:w
- 激活函数:sigmoid
- 本质上,逻辑回归 = 感知机 + 概率解释。
损失函数联系
- 逻辑回归的交叉熵损失是深度学习分类模型的标准选择。
- 在多分类问题中,逻辑回归自然扩展为 softmax 回归(Softmax Regression),其损失函数就是 softmax + cross entropy。
优化方式
- 逻辑回归参数求解过程使用梯度下降,与神经网络训练一致。
- 可以使用 SGD、Adam 等优化器来加速收敛。
基础性地位
- 逻辑回归是深度学习的入口模型,帮助理解神经网络的前向传播、反向传播和损失函数。
- 在 NLP(如词向量 + LR)、CV(如特征提取 + LR)等场景中,逻辑回归常作为基准模型。
逻辑回归的应用场景
二分类任务
- 垃圾邮件识别(spam vs. not spam)
- 广告点击预测(点击 vs. 不点击)
- 医疗诊断(二分类疾病预测)
作为大模型的最后一层
- 在深度神经网络、卷积网络、Transformer 中,最后一层往往是一个逻辑回归(或 softmax 回归),将隐藏特征映射为概率输出。
线性可分数据
- 逻辑回归天然适用于线性可分或近似线性可分的数据集。
逻辑回归的改进与扩展
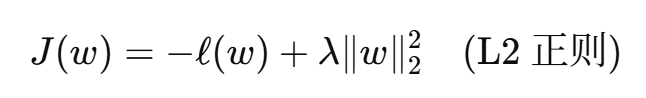
正则化
-
为防止过拟合,逻辑回归常加入正则化项:
-
L1 正则还能实现特征选择(稀疏化)。
多分类扩展
- 使用 softmax 回归(多项逻辑回归)实现多分类。
核逻辑回归
- 引入核函数,将输入映射到高维空间,增强非线性建模能力。
与深度学习结合
- 在神经网络中,逻辑回归层常作为输出层。
- 对抗学习(GAN)、序列建模中,逻辑回归思想用于判别器。
实践中的逻辑回归
训练流程
- 数据预处理(归一化、标准化、特征选择)
- 参数初始化(通常为零或小随机数)
- 前向计算(线性 + sigmoid)
- 计算损失(交叉熵)
- 反向传播(梯度计算)
- 参数更新(SGD/Adam 等优化器)
- 模型评估(准确率、AUC、F1)
超参数调节
- 学习率:影响收敛速度和稳定性;
- 正则化系数:平衡拟合能力和泛化性能;
- 特征处理:对性能影响远大于参数本身。
与深度学习框架结合
在 TensorFlow、PyTorch 中,逻辑回归的实现通常只需一层线性层 + sigmoid 激活,再加上 BCE(Binary Cross Entropy)损失即可。
