当前位置：首页 > news >正文

深入理解跳表（Skip List）：原理、实现与应用

news 2025/9/15 6:55:07

一、什么是跳表？

1.1 基本思想

1.2 随机层数的引入

二、跳表的效率保证

2.1 随机层数的生成

2.2 平均层数与空间复杂度

2.3 时间复杂度

三、跳表的实现

四、跳表 vs 平衡树 vs 哈希表

4.1 跳表的优势

4.2 跳表的劣势

五、总结

参考文献

跳表（Skip List）是一种基于概率的高效动态数据结构，支持快速查找、插入和删除操作，其时间复杂度可达到O(logN)。本文将深入探讨跳表的原理、实现细节，并通过代码示例和图表分析其性能优势。

一、什么是跳表？

跳表（Skip List）是一种用于解决查找问题的数据结构，与平衡搜索树（如AVL树、红黑树）和哈希表具有相同的功能，可用于实现键或键值对的查找模型。跳表由William Pugh于1990年在其论文《Skip Lists: A Probabilistic Alternative to Balanced Trees》中首次提出。

1.1 基本思想

跳表基于有序链表构建。在普通有序链表中，查找的时间复杂度为O(N)。为了提升效率，跳表引入了“多层”链表的概念：

第一层：所有节点按顺序连接。
第二层：每两个节点中选取一个作为“索引”，指向下一层的对应节点。
更高层：依此类推，每一层的节点数约为下一层的一半。

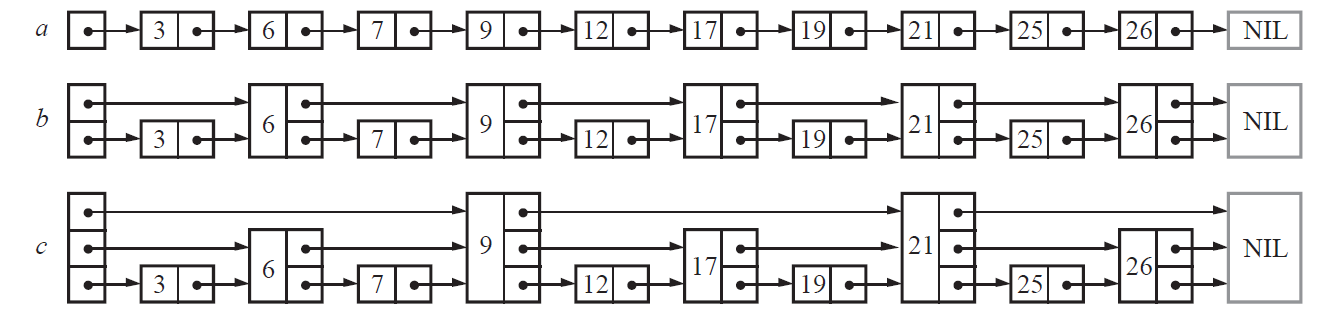
这样，查找过程类似于二分查找，时间复杂度可优化至O(logN)。

1.2 随机层数的引入

若严格保持上下两层节点数2:1的比例，插入和删除操作会破坏结构，导致重新调整的开销。跳表通过随机层数的方式解决这一问题：每个新插入节点的层数由随机函数决定，不再严格保持比例关系，从而保证操作的高效性。

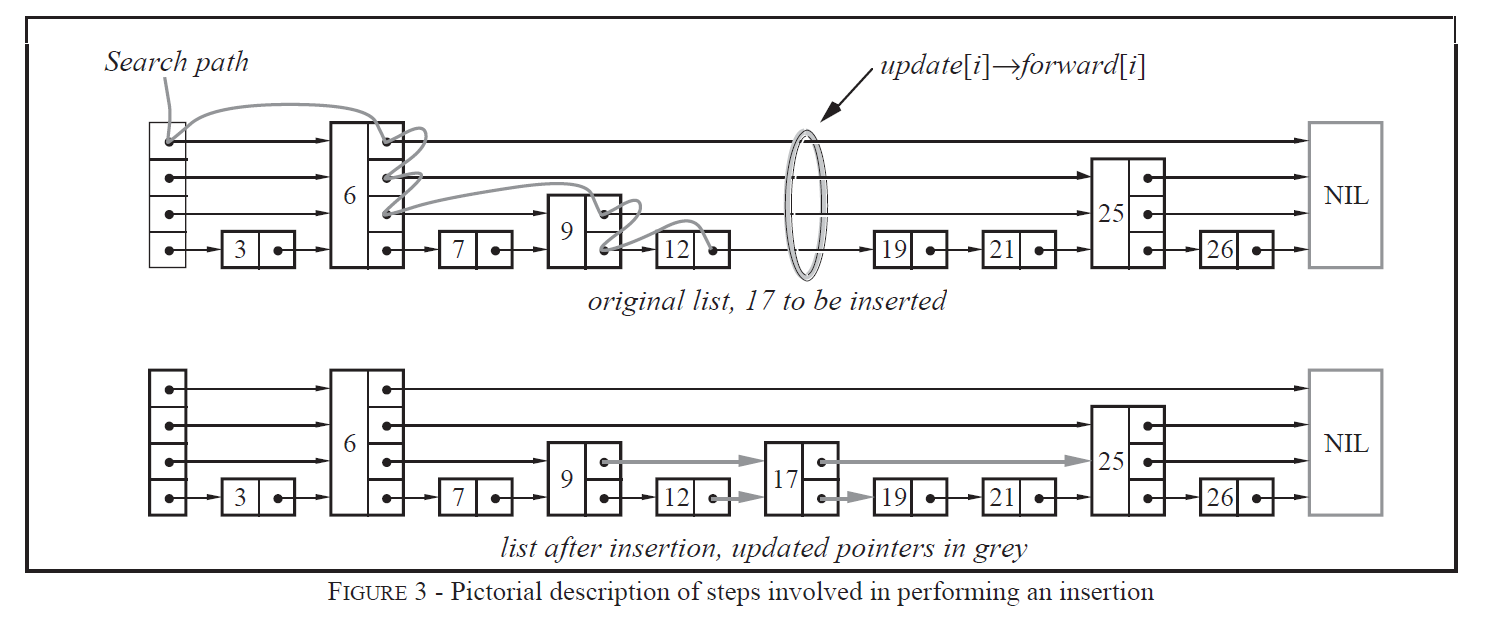
二、跳表的效率保证

2.1 随机层数的生成

跳表通常设定一个最大层数maxLevel和一个概率值p。生成随机层数的伪代码如下：

def randomLevel():lvl = 1while random() < p and lvl < maxLevel:lvl += 1return lvl

在Redis的skiplist实现中，这两个参数的取值为：

p = 1/4

maxLevel = 32

2.2 平均层数与空间复杂度

根据前面randomLevel()的伪码，我们很容易看出，产生越高的节点层数，概率越低。定量的分析如下：

节点层数至少为1。而大于1的节点层数，满足一个概率分布。
节点层数恰好等于1的概率为1-p。
节点层数大于等于2的概率为p，而节点层数恰好等于2的概率为p(1-p)。
节点层数大于等于3的概率为p^2，而节点层数恰好等于3的概率为p^2*(1-p)。
节点层数大于等于4的概率为p^3，而节点层数恰好等于4的概率为p^3*(1-p)。

因此，一个节点的平均层数（也即包含的平均指针数目），计算如下：

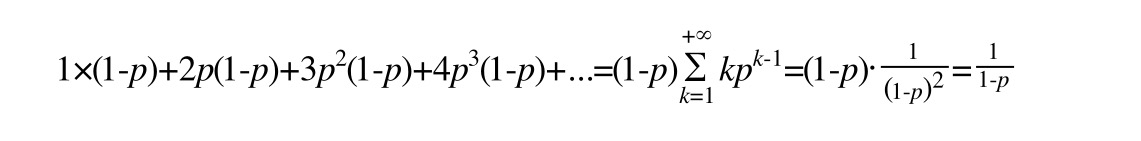
现在很容易计算出：

当p=1/2时，每个节点所包含的平均指针数目为2；

当p=1/4时，每个节点所包含的平均指针数目为1.33。

2.3 时间复杂度

跳表的查找、插入、删除操作的时间复杂度均为O(logN)，其推导过程较为复杂，需要有一定的数据功底，有兴趣的老铁，可以参考以下文章中的讲解：

铁蕾大佬的博客：：http://zhangtielei.com/posts/blog-redis-skiplist.html

William_Pugh大佬的论文：ftp://ftp.cs.umd.edu/pub/skipLists/skiplists.pdf

三、跳表的实现

以下是一个基于C++的跳表实现示例，包含搜索、插入、删除等操作：

https://leetcode.cn/problems/design-skiplist/

#include <iostream>
#include <vector>
#include <cstdlib>
#include <ctime>
#include <random>
#include <chrono>struct SkiplistNode {int _val;std::vector<SkiplistNode*> _nextV;SkiplistNode(int val, int level) : _val(val), _nextV(level, nullptr) {}
};class Skiplist {typedef SkiplistNode Node;
public:Skiplist() {srand(time(0));_head = new Node(-1, 1);}bool search(int target) {Node* cur = _head;int level = _head->_nextV.size() - 1;while (level >= 0) {if (cur->_nextV[level] && cur->_nextV[level]->_val < target) {cur = cur->_nextV[level];} else if (!cur->_nextV[level] || cur->_nextV[level]->_val > target) {level--;} else {return true;}}return false;}std::vector<Node*> findPrevNodes(int num) {Node* cur = _head;int level = _head->_nextV.size() - 1;std::vector<Node*> prevV(level + 1, _head);while (level >= 0) {if (cur->_nextV[level] && cur->_nextV[level]->_val < num) {cur = cur->_nextV[level];} else {prevV[level] = cur;level--;}}return prevV;}void add(int num) {auto prevV = findPrevNodes(num);int n = randomLevel();Node* newNode = new Node(num, n);if (n > _head->_nextV.size()) {_head->_nextV.resize(n, nullptr);prevV.resize(n, _head);}for (int i = 0; i < n; i++) {newNode->_nextV[i] = prevV[i]->_nextV[i];prevV[i]->_nextV[i] = newNode;}}bool erase(int num) {auto prevV = findPrevNodes(num);if (!prevV[0]->_nextV[0] || prevV[0]->_nextV[0]->_val != num) {return false;}Node* del = prevV[0]->_nextV[0];for (size_t i = 0; i < del->_nextV.size(); i++) {prevV[i]->_nextV[i] = del->_nextV[i];}delete del;// 降低头节点层数（若最高层为空）int i = _head->_nextV.size() - 1;while (i >= 0 && _head->_nextV[i] == nullptr) i--;_head->_nextV.resize(i + 1);return true;}int randomLevel() {int level = 1;while ((rand() / (double)RAND_MAX) < _p && level < _maxLevel) {level++;}return level;}private:Node* _head;size_t _maxLevel = 32;double _p = 0.25;
};

四、跳表 vs 平衡树 vs 哈希表

特性	跳表	平衡树（AVL/红黑树）	哈希表
时间复杂度	O(logN)	O(logN)	O(1)（平均）
空间复杂度	较低（p=1/4时≈1.33）	较高（每个节点多指针）	中等（需扩容）
实现难度	简单	复杂	中等
是否有序	是	是	否
扩容开销	无	无	有