当前位置：首页 > news >正文

MX模拟赛总结

news 2025/9/14 14:32:07

T1

题面：

很水的一道题，硬生生被题目搞没了 50pts……

首先我要说明一件事：这个题目实际上就是把按照第 $i$ 位四舍五入的过程给你仔细地说明了一下，代码非常好写，这里我不多展开。

然后我来说一说我被题目搞没 50pts 是为什么。注意看这句话：

需要注意的是，第 $1$ 位即使进位，也不会改变我们上面约定的位数的编号规则。

这句话很好理解嘛，就是编号一直保持 $1,2,…,k1,2,\dots,k$ 嘛，不会因为第一位进位变成 $0,1,2,…,k0,1,2,\dots,k$ 或者 $1,2,…,k,k+11,2,\dots,k,k+1$ 。

然后我们再来看输出：

你需要具体输出每一步后的结果，从原数开头。

现在我们来思考一个事：这个原数开头是指从 $1→k1\to k$ 还是 $0→k0\to k$ 。

首先解释一下这个 $a_0$ 是什么： $a_0$ 就是第一位进位后的值。前面说了：第一位即使进位，编号也不变。那不就是最高位的编号永远是 $1$ 咯？那这么说输出也就只需要输出 $1→k1\to k$ 就行了？但是这明显不对啊，原数不是还有一个 $a_0$ 吗？这一位不输出？

然后我就就着这个问题思考了一个小时，最终我选择：不输出 $a_0$ 。然后没了 50pts……

所以这真的不是我的错，实在是题目太……抽象了。

T2

题面：

首先这题很容易想到二维 DP，于是我们可以写出一份超级暴力的代码：

for(int i=1;i<=n;i++)
{for(int j=1;j<=m;j++){for(int k=0;k<i;k++){for(int l=1;l<=m;l++){if(a[i][j]>a[k][l]){dp[i][j]=max(dp[i][j],dp[k][l]+1);}}}}
}

但是很明显这份代码过不了，稍微一算时间复杂度就知道：这代码能过我吃。

那怎么优化呢？这里有很多大佬会说：用线段树啊！线段树不是直接秒了吗。这里确实可以用线段树，不过本蒟蒻太菜了，想到可以用线段树但写不来，于是我用了三个 DP。

在这之前，我们要先搞清楚如果要用线段树大致该怎么写：首先肯定对于每一排要求区间最大值，然后还要把每一行的区间最大值再求一次区间最大值，这样时间复杂度才稍微正常一点（差不多是 $O(nmlog⁡nlog⁡m)O(nm\log n\log m)$ 左右），那现在我们不会线段树，我们要用数组去模拟这个区间最大值，该怎么办呢？我的想法是这样的：

定义 g[i][j] 表示在第 $i$ 行且在第 $j$ 列左边的所有 dp 值中的最大值。
定义 f[i][j] 表示在第 $i$ 行上面且在第 $j$ 列左边的所有 g 值中的最大值。

然后我们就可以写出转移方程：

$dp_{i,j}=\max\{dp_{i,j},f_{i,j}+1\}$

$g_{i,j+1}=\max\{g_{i,j},dp_{i,j}\}$

$f_{i+1,j}=\max\{f_{i,j},g_{i,j}\}$

然后就可以愉快地写代码了：

#include<bits/stdc++.h>
#define code using
#define by namespace
#define plh std
code by plh;
int n,m,a[1006][1006],dp[1006][1006],g[1006][1006],f[1006][1006],b[1006][1006];
signed main()
{
//	freopen("lis.in","r",stdin);
//	freopen("lis.out","w",stdout);cin>>m>>n;for(int i=1;i<=n;i++){for(int j=1;j<=m;j++){scanf("%d",&a[i][j]);b[i][a[i][j]]=1;}}int ans=0;for(int i=1;i<=n;i++){for(int j=0;j<=1000;j++){if(b[i][j]){dp[i][j]=max(dp[i][j],f[i][j]+1);}g[i][j+1]=max(g[i][j],dp[i][j]);f[i+1][j]=max(f[i][j],g[i][j]);ans=max(ans,dp[i][j]);}}printf("%d",ans);return 0;
}

这里再顺便提一下线段树做法：建一棵权值线段树，按照 $a_i$ 建的，每个点保存它当前最大的 DP 值，总时间复杂度大概 $O(nm\log(\max_{i=1}^n\{a_i\}))$ 。

（代码自己写）。

T3

题面：

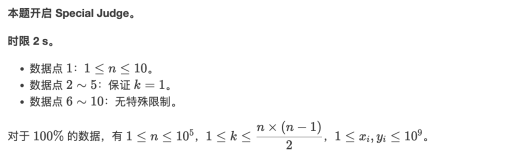
首先看到这种二元分式，第一反应应该是二分，因为这样可以把问题转变成一个判定性问题，要好做一点。

因为题目中说了对计算结果从大到小排序，所以单调性是肯定可以保证的，现在来思考如何确定我二分到的这个值是否是第 $k$ 大的。

要看是否是第 $k$ 大的，我们只需要看看比这个值还要大的值有多少就行了，现假设下面这个不等式成立：

$x<xiyi+xjyjxi+xjx\lt\cfrac{x_iy_i+x_jy_j}{x_i+x_j}$

（ $x$ 为我当前二分出来的值）。

通过变换：

$xxi+xxj<xiyi+xjyjxx_i+xx_j\lt x_iy_i+x_jy_j$

$∴xxi−xiyi<xjyj−xxj\therefore xx_i-x_iy_i\lt x_jy_j-xx_j$

设函数 $f(k)=xx_k-x_ky_k$ ，则：

$∴f(i)<−f(j)\therefore f(i)\lt-f(j)$

这时我们会发现原不等式变成了这个鬼样子。

因此我们可以把 $f (i)$ 装在一个数组里面，把 $- f (j)$ 装在一个数组里面，然后找满足这个不等式的数对 $(i, j)$ 有多少个，最后判断一下就行了。

代码：

#include<bits/stdc++.h>
#define int long long
#define code using
#define by namespace
#define plh std
code by plh;
int n,k;
const double eps=1e-5;
double x[100006],y[100006],a[100006],b[100006];
bool cmp(double x,double y)
{return x<y;
}
bool check(double s)
{int num=0;for(int i=1;i<=n;i++){a[i]=x[i]*y[i]-s*x[i];b[i]=s*x[i]-x[i]*y[i];if(b[i]-a[i]<eps)//不能自己跟自己运算{num--;}}sort(a+1,a+n+1,cmp);sort(b+1,b+n+1,cmp);for(int i=1,j=0;i<=n;i++){while(b[j+1]-a[i]<eps&&j+1<=n)//用双指针降低时间复杂度{j++;}num+=j;}return num/2<k;//如果 i,j 互换一下不等式依然成立，所以这里我们要除以一个 2
}
signed main()
{cin>>n>>k;for(int i=1;i<=n;i++){cin>>x[i]>>y[i];}double l=1.0,r=1000000000.0,mid=0.0;while(r-l>eps){mid=(l+r)/2;if(check(mid))//mid 太大了，满足不等式的数对太少了{r=mid;}else{l=mid;}}printf("%0.5lf",l);return 0;
}

T4

题面：

我们常说做一道题首先要关注它的数据范围，这里不难发现一个很奇怪的点： $0≤ai≤20\le a_i\le2$ 。这是为什么？为什么要限制 $a_i$ 只有 $0, 1, 2$ 三种数。

再看题目中求的：点权和为 $k$ 的连通块数量。其中 $+ 0$ 没有任何效果， $+ 1$ 可以改变奇偶性， $+ 2$ 只能增加和的大小。所以不难看出： $+ 1$ 是一个很特殊的情况，因为只有它可以改变奇偶性。

因此我们可以记录下当前的点权和，然后记录下 $1$ 的个数，最后看看减多少个 $1$ 才能让它们的奇偶性相同（因为这时减 $2$ 就可以了）。

代码：

#include<bits/stdc++.h>
#define int long long
#define code using
#define by namespace
#define plh std
code by plh;
struct Node{int sum,mnone,cnt[3];Node(){sum=0,mnone=LONG_LONG_MAX;memset(cnt,0,sizeof(cnt));}
};
Node operator + (const Node a,const Node b)
{Node c=Node();c.sum=a.sum+b.sum;c.mnone=min(a.mnone,b.mnone);for(int i=0;i<3;i++){c.cnt[i]=a.cnt[i]+b.cnt[i];}return c;
}
int t,n,k,ans,a[1000006];
vector<int>v[1000006];
bool check(Node x)
{if(x.sum<k)//连总和都不够{return false;}if((x.cnt[1]&1)==(k&1))//奇偶性相同，直接减就好了{return true;}if(x.sum-x.mnone+1>=k)//如果减去含有 1 的点权和最小的子树的点权和还够的话，那就随便了{return true;}return false;//反之不成立
}
Node dfs(int x,int fa)//从最底下开始计算，主要是贪心
{Node b=Node();for(auto i:v[x]){if(i==fa){continue;}b=b+dfs(i,x);}b.sum+=a[x];b.cnt[a[x]]++;if(a[x]==1){b.mnone=min(b.mnone,b.sum);}if(check(b))//如果可以，直接变成一个连通快{b=Node();ans++;}return b;
}
signed main()
{cin>>t;while(t--){cin>>n>>k;for(int i=1;i<=n;i++){cin>>a[i];}for(int i=1,x,y;i<n;i++){cin>>x>>y;v[x].push_back(y);v[y].push_back(x);}dfs(1,0);cout<<ans<<'\n';ans=0;for(int i=1;i<=n;i++){v[i].clear();}}return 0;
}