动态规划解决网格路径问题

目录

一、不同路径（LeetCode 62）

二、不同路径 II（LeetCode 63） 

三、下降路径最小和（LeetCode 931）

四、最小路径和（LeetCode 64） 

五、地下城游戏（LeetCode 174） 

总结

---

在算法的世界里，网格路径类问题是动态规划（DP）应用的经典场景。这类问题通常围绕在网格中寻找特定路径展开，比如计算不同路径数量、最小路径和等。下面就来详细探讨如何用动态规划解决这类问题。

一、不同路径（LeetCode 62）

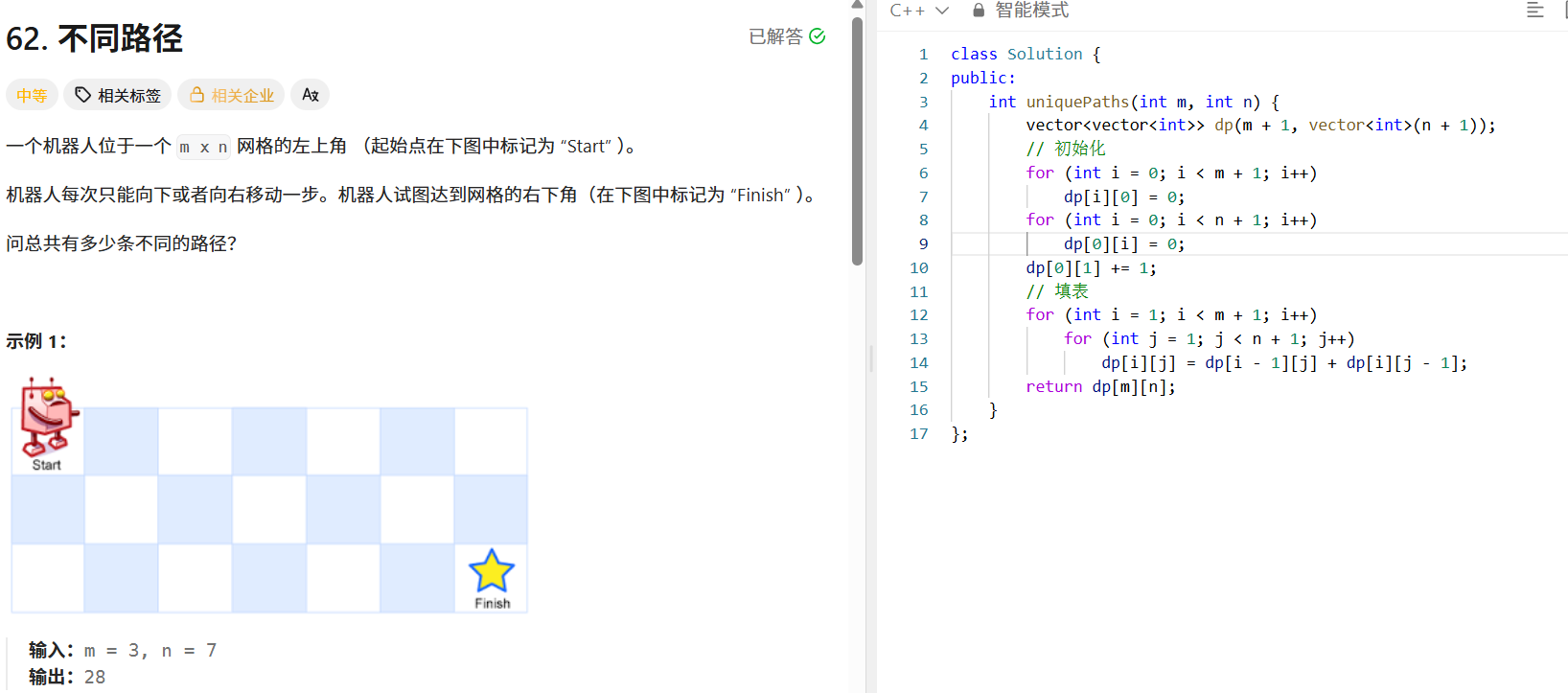
问题描述
 
一个机器人位于  m x n  网格的左上角，每次只能向下或向右移动一步，求到达右下角的不同路径总数。
 
解题思路
 
- 状态定义：设  dp[i][j]  表示从左上角到达  (i, j)  位置的不同路径数。
- 状态转移：因为只能从上方（ dp[i - 1][j] ）或左方（ dp[i][j - 1] ）到达  (i, j) ，所以  dp[i][j] = dp[i - 1][j] + dp[i][j - 1] 。
- 初始化：第一行（ i = 0 ）的每个位置只能从左边过来，所以  dp[0][j] = 1 ；第一列（ j = 0 ）的每个位置只能从上面过来，所以  dp[i][0] = 1 。
 
代码实现
 

class Solution {
public:int uniquePaths(int m, int n) {vector<vector<int>> dp(m, vector<int>(n, 0));// 初始化第一列for (int i = 0; i < m; i++) {dp[i][0] = 1;}// 初始化第一行for (int j = 0; j < n; j++) {dp[0][j] = 1;}// 状态转移for (int i = 1; i < m; i++) {for (int j = 1; j < n; j++) {dp[i][j] = dp[i - 1][j] + dp[i][j - 1];}}return dp[m - 1][n - 1];}
};

二、不同路径 II（LeetCode 63） 

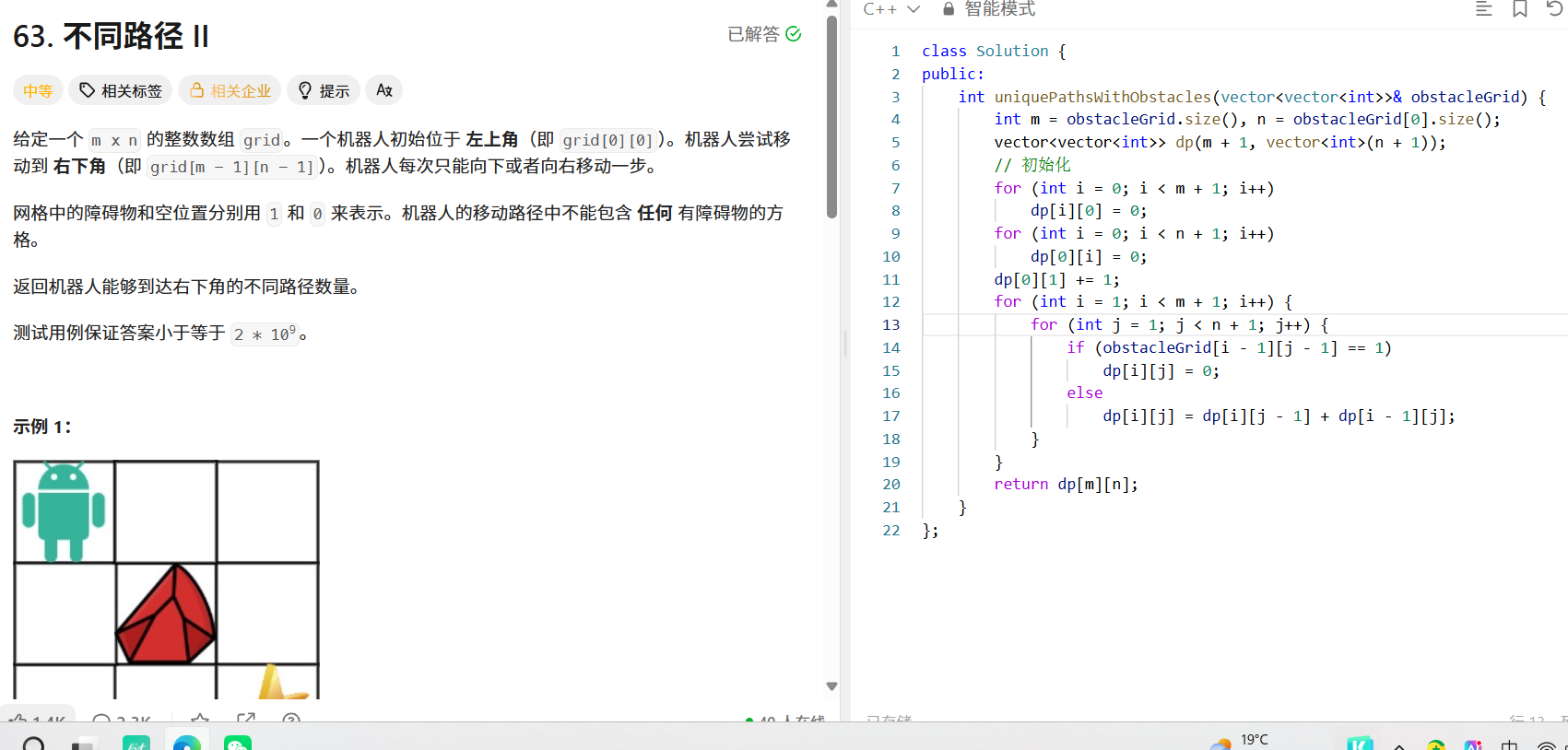
问题描述
 
在不同路径的基础上，网格中存在障碍物（用  1  表示），障碍物位置无法通过，求到达右下角的不同路径数。
 
解题思路
 
- 状态定义和转移与“不同路径”类似，但遇到障碍物时， dp[i][j] = 0 （表示此路不通）。
- 初始化时，若第一行或第一列存在障碍物，障碍物及之后的位置  dp  值都为  0 。
 
代码实现
 

class Solution {
public:int uniquePathsWithObstacles(vector<vector<int>>& obstacleGrid) {int m = obstacleGrid.size();int n = obstacleGrid[0].size();vector<vector<int>> dp(m, vector<int>(n, 0));// 初始化第一列for (int i = 0; i < m && obstacleGrid[i][0] == 0; i++) {dp[i][0] = 1;}// 初始化第一行for (int j = 0; j < n && obstacleGrid[0][j] == 0; j++) {dp[0][j] = 1;}// 状态转移for (int i = 1; i < m; i++) {for (int j = 1; j < n; j++) {if (obstacleGrid[i][j] == 0) {dp[i][j] = dp[i - 1][j] + dp[i][j - 1];} else {dp[i][j] = 0;}}}return dp[m - 1][n - 1];}
};

三、下降路径最小和（LeetCode 931）

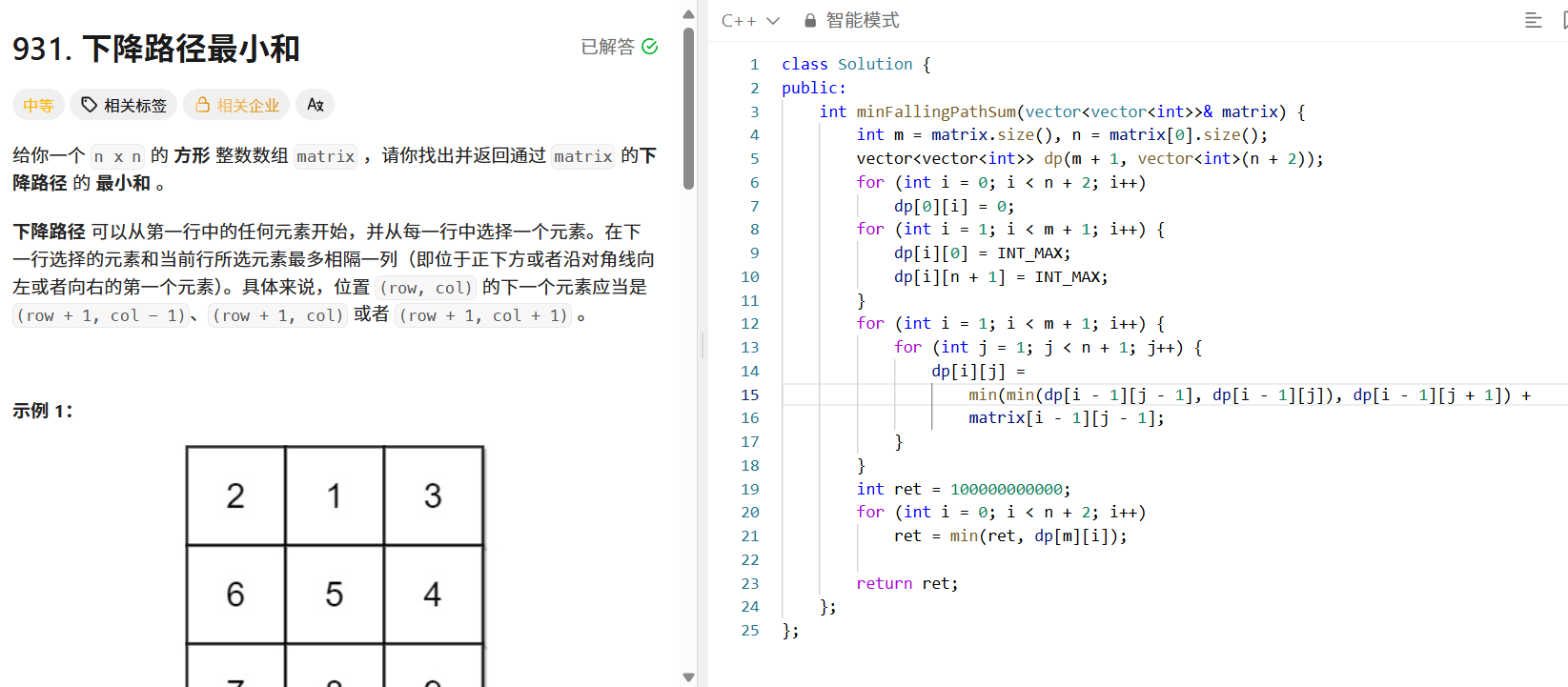
问题描述
 
给定  n x n  矩阵，下降路径可从第一行任意元素开始，下一行元素与当前行元素最多隔一列（正下方、左下方、右下方），求下降路径的最小和。
 
解题思路
 
- 状态定义： dp[i][j]  表示到达第  i  行第  j  列的最小下降路径和。
- 状态转移： dp[i][j] = min(dp[i - 1][j - 1], dp[i - 1][j], dp[i - 1][j + 1]) + matrix[i][j] ，需注意边界情况（列首和列尾）。
- 初始化：第一行的  dp  值就是矩阵第一行对应元素值。
 
代码实现

class Solution {
public:int minFallingPathSum(vector<vector<int>>& matrix) {int n = matrix.size();vector<vector<int>> dp(n, vector<int>(n, 0));// 初始化第一行for (int j = 0; j < n; j++) {dp[0][j] = matrix[0][j];}// 状态转移for (int i = 1; i < n; i++) {for (int j = 0; j < n; j++) {int minVal = dp[i - 1][j];if (j > 0) {minVal = min(minVal, dp[i - 1][j - 1]);}if (j < n - 1) {minVal = min(minVal, dp[i - 1][j + 1]);}dp[i][j] = minVal + matrix[i][j];}}// 找最后一行的最小值int minSum = dp[n - 1][0];for (int j = 1; j < n; j++) {minSum = min(minSum, dp[n - 1][j]);}return minSum;}
};

四、最小路径和（LeetCode 64） 

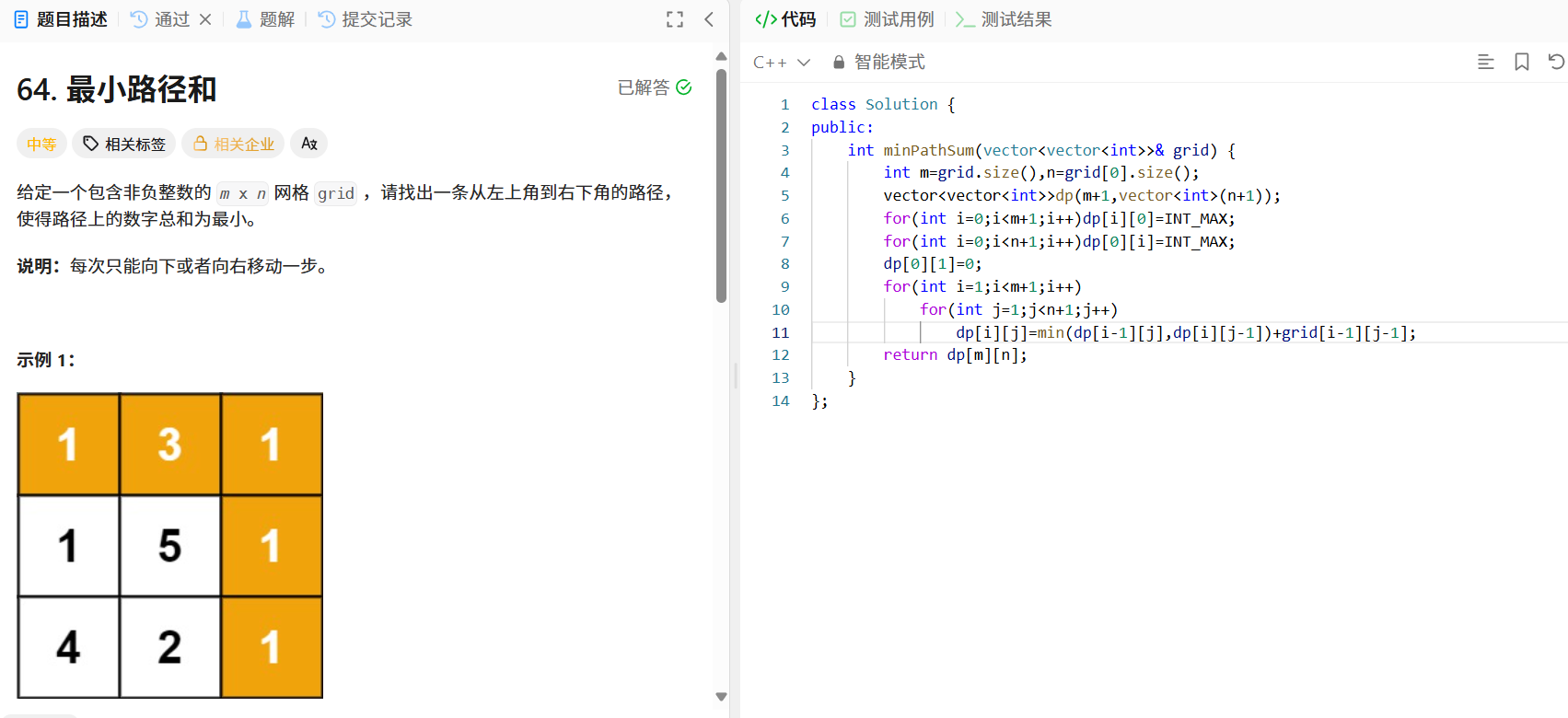
问题描述
 
给定  m x n  非负整数网格，每次只能向下或向右移动，求从左上角到右下角路径上数字总和的最小值。
 
解题思路
 
- 状态定义： dp[i][j]  表示从左上角到  (i, j)  的最小路径和。
- 状态转移： dp[i][j] = min(dp[i - 1][j], dp[i][j - 1]) + grid[i][j] 。
- 初始化：第一行  dp[0][j] = dp[0][j - 1] + grid[0][j] ；第一列  dp[i][0] = dp[i - 1][0] + grid[i][0] 。
 
代码实现
 

class Solution {
public:int minPathSum(vector<vector<int>>& grid) {int m = grid.size();int n = grid[0].size();vector<vector<int>> dp(m, vector<int>(n, 0));// 初始化第一列dp[0][0] = grid[0][0];for (int i = 1; i < m; i++) {dp[i][0] = dp[i - 1][0] + grid[i][0];}// 初始化第一行for (int j = 1; j < n; j++) {dp[0][j] = dp[0][j - 1] + grid[0][j];}// 状态转移for (int i = 1; i < m; i++) {for (int j = 1; j < n; j++) {dp[i][j] = min(dp[i - 1][j], dp[i][j - 1]) + grid[i][j];}}return dp[m - 1][n - 1];}
};

五、地下城游戏（LeetCode 174） 

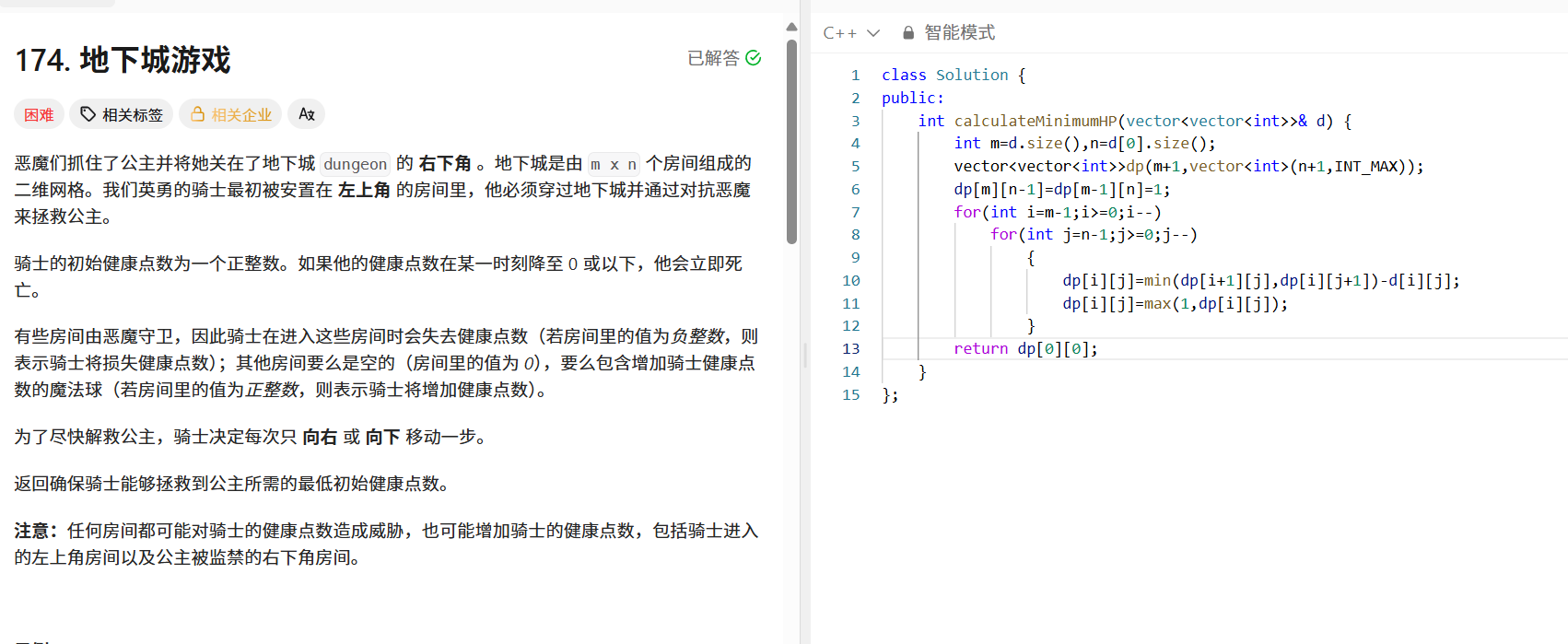
问题描述
 
骑士从左上角到右下角救公主，房间值为负表示损失健康，正表示增加健康，健康值不能≤0，求初始最低健康值。
 
解题思路
 
- 状态定义： dp[i][j]  表示从  (i, j)  到右下角所需的最低初始健康值。
- 状态转移：从右边（ dp[i][j + 1] ）或下边（ dp[i + 1][j] ）过来， dp[i][j] = max(1, min(dp[i + 1][j], dp[i][j + 1]) - dungeon[i][j]) ， max(1, ...)  保证健康值至少为  1 。
- 初始化：右下角  dp[m - 1][n - 1] = max(1, 1 - dungeon[m - 1][n - 1]) ，边界（最后一行和最后一列）单独处理。
 
代码实现

class Solution {
public:int minPathSum(vector<vector<int>>& grid) {int m = grid.size();int n = grid[0].size();vector<vector<int>> dp(m, vector<int>(n, 0));// 初始化第一列dp[0][0] = grid[0][0];for (int i = 1; i < m; i++) {dp[i][0] = dp[i - 1][0] + grid[i][0];}// 初始化第一行for (int j = 1; j < n; j++) {dp[0][j] = dp[0][j - 1] + grid[0][j];}// 状态转移for (int i = 1; i < m; i++) {for (int j = 1; j < n; j++) {dp[i][j] = min(dp[i - 1][j], dp[i][j - 1]) + grid[i][j];}}return dp[m - 1][n - 1];}
};

总结

网格路径类动态规划问题的核心在于：
 
1. 合理定义状态，明确  dp[i][j]  所代表的含义。
2. 找出状态转移方程，分析当前状态与之前状态的关系。
3. 正确初始化边界条件，确保动态规划过程的正确性。
通过对这几道经典题目进行分析，能更好地掌握动态规划在网格路径问题中的应用方法，为解决更复杂的算法问题打下基础。