DENOISING DIFFUSION IMPLICIT MODELS
摘要:
去噪扩散概率模型(Denoising Diffusion Probabilistic Models,DDPMs)无需对抗训练即可实现高质量的图像生成,但生成样本时需要模拟多步马尔可夫链。为加速采样过程,提出了去噪扩散隐模型(Denoising Diffusion Implicit Models,DDIMs),这是一类更高效的迭代隐概率模型,其训练过程与DDPMs相同。在DDPMs中,生成过程被定义为特定马尔可夫扩散过程的逆过程。我们通过一类非马尔可夫扩散过程对DDPMs进行了推广,这些过程可得到相同的训练目标。这些非马尔可夫过程可对应于确定性的生成过程,从而产生能更快生成高质量样本的隐模型。我们的实证研究表明,与DDPMs相比,DDIMs在挂钟时间(即实际运行时间)方面能够以10倍至50倍的速度生成高质量样本,使我们能够在计算量和样本质量之间进行权衡,直接在潜在空间中进行语义上有意义的图像插值,并以极低的误差重建观测结果。
总而言之,DDIM 的核心思想是:在保持 DDPM 训练方式不变的前提下,通过改变采样过程的定义(从马尔可夫变为非马尔可夫),实现了数量级级别的采样加速,并获得了如确定性生成、隐空间插值等新特性。
讨论:
我们从纯粹的变分视角出发,介绍了去噪扩散隐模型(DDIMs)——一种利用去噪自编码/得分匹配目标进行训练的隐式生成模型。DDIM能够比现有的去噪扩散概率模型(DDPMs)和噪声条件评分网络(NCSNs)更高效地生成高质量样本,并且具备从潜在空间进行有意义的插值的能力。此处提出的非马尔可夫前向过程似乎表明,除了高斯过程之外,还存在其他连续的前向过程(这在原始扩散框架中是无法实现的,因为在原始框架中,高斯分布是唯一具有有限方差的稳定分布)。此外,我们在附录A中还展示了一个多项式前向过程的离散案例,探究其他组合结构中类似的替代方案也将颇具趣味。
再者,由于DDIMs的采样过程与神经常微分方程(ODE)的采样过程相似,因此探究能否利用减小ODE离散化误差的方法(包括诸如Adams-Bashforth(Butcher & Goodwin, 2008)等多步方法)来帮助在更少的步骤内进一步提升样本质量(Queiruga et al., 2020),也将是一件很有意义的事情。此外,探究DDIMs是否具备现有隐式模型的其他特性(Bau et al., 2019)同样值得关注。
前言:
深度生成模型已在多个领域展现出生成高质量样本的能力(Karras等人,2020年;van den Oord等人,2016a)。在图像生成方面,生成对抗网络(GANs,Goodfellow等人,2014年)目前展现出的样本质量高于基于似然的方法,如变分自编码器(Kingma & Welling,2013年)、自回归模型(van den Oord等人,2016b)以及归一化流模型(Rezende & Mohamed,2015年;Dinh等人,2016年)。然而,GANs需要针对优化和架构做出非常特定的选择,才能稳定训练过程(Arjovsky等人,2017年;Gulrajani等人,2017年;Karras等人,2018年;Brock等人,2018年),并且可能无法覆盖数据分布的所有模式(Zhao等人,2018年)。
近期,关于迭代生成模型的研究(Bengio等人,2014年),如去噪扩散概率模型(DDPM,Ho等人,2020年)和噪声条件评分网络(NCSN,Song & Ermon,2019年),已展现出无需对抗训练即可生成与生成对抗网络(GANs)相媲美的样本的能力。为实现这一目标,众多去噪自编码模型被训练用于对受不同水平高斯噪声破坏的样本进行去噪。随后,样本通过一个马尔可夫链生成,该链从白噪声开始,逐步将其去噪为图像。这种生成马尔可夫链过程要么基于朗之万动力学(Song & Ermon,2019年),要么通过逆转一个前向扩散过程来获得,该前向扩散过程会逐步将图像转化为噪声(Sohl-Dickstein等人,2015年)。
这些模型的一个关键缺陷在于,它们需要多次迭代才能生成高质量样本。以去噪扩散概率模型(DDPMs)为例,这是因为其生成过程(从噪声到数据)近似于前向扩散过程(从数据到噪声)的逆过程,而该前向扩散过程可能包含数千个步骤;要生成单个样本,必须遍历所有这些步骤,这使得其生成速度远慢于只需通过网络进行一次前向传播的生成对抗网络(GANs)。例如,在英伟达2080 Ti GPU上,从DDPM中采样生成5万张32×32大小的图像大约需要20小时,而从GAN中采样生成同样数量的图像则不到一分钟。对于更大尺寸的图像而言,这一问题会更加突出,因为在同一款GPU上,采样生成5万张256×256大小的图像可能需要近1000小时。
为缩小去噪扩散概率模型(DDPMs)与生成对抗网络(GANs)之间的效率差距,我们提出了去噪扩散隐模型(DDIMs)。DDIMs属于隐式概率模型(Mohamed & Lakshminarayanan, 2016),从某种意义上说,它们与DDPMs紧密相关,因为二者采用相同的目标函数进行训练。
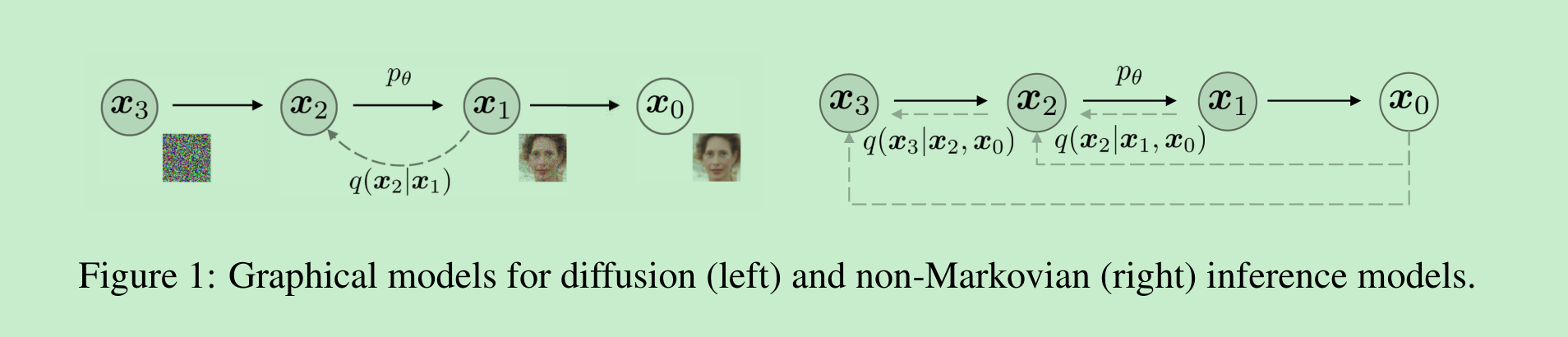
在第3节中,我们将去噪扩散概率模型(DDPMs)所使用的马尔可夫前向扩散过程推广至非马尔可夫过程,并仍能够针对这些非马尔可夫过程设计出合适的逆向生成马尔可夫链。我们证明,由此得出的变分训练目标具有一个共同的替代目标,而该目标恰好就是用于训练DDPM的目标。因此,只需选择不同的非马尔可夫扩散过程(第4.1节)及相应的逆向生成马尔可夫链,我们便可在使用同一神经网络的情况下,从一大类生成模型中自由选择。特别是,我们能够采用非马尔可夫扩散过程,这些过程会生成“简短”的生成马尔可夫链(第4.2节),可在少量步骤内完成模拟。这能在样本质量仅有微小损失的情况下,大幅提升样本生成效率。
在第5节中,我们展示了去噪扩散隐模型(DDIMs)相较于去噪扩散概率模型(DDPMs)的若干实证优势。首先,当我们采用所提方法将采样速度提升10倍至100倍时,DDIMs生成的样本质量优于DDPMs。其次,DDIM样本具有以下“一致性”特性,而DDPMs不具备:若从相同的初始潜在变量出发,利用不同长度的马尔可夫链生成多个样本,这些样本将呈现出相似的高级特征。第三,由于DDIMs具有“一致性”,我们可以通过操纵DDIMs中的初始潜在变量来实现语义上有意义的图像插值,而DDPMs由于生成过程具有随机性,只能在图像空间附近进行插值。
背景
给定来自数据分布 q(x0)q(x_0)q(x0) 的样本,我们有兴趣学习一个近似于q(x0)q(x_0)q(x0)且易于采样的模型分布pθ(x0)p_\theta(x_0)pθ(x0)。去噪扩散概率模型(DDPMs, Sohl-Dickstein 等人 (2015);Ho 等人 (2020))是以下形式的潜在变量模型:
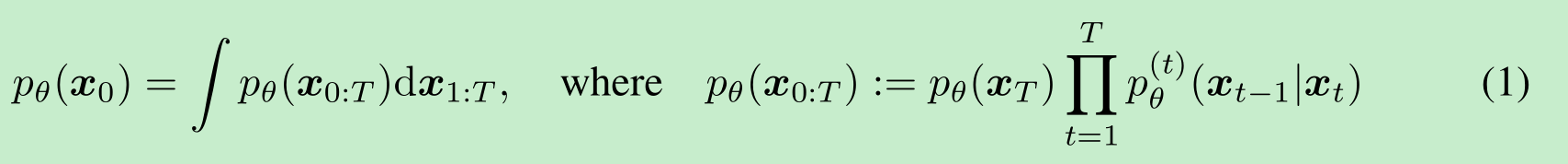
其中x1,…,xTx_1, \ldots, x_Tx1,…,xT 是与x0x_0x0 在同一样本空间中的潜在变量(记为 X\mathcal{X}X)。参数 θ\thetaθ被学习(即优化确定),通过最大化变分下界来拟合数据分布q(x0)q(x_0)q(x0):
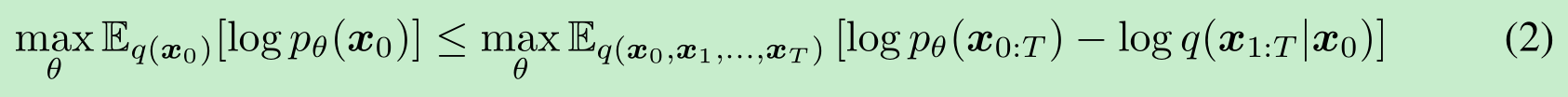
(这里公式二,我个人感觉他是写错了,我怎么推导都不对,下面是我的推导) 
其中 q(x1:T∣x0)q(x_{1:T} \mid x_0)q(x1:T∣x0) 是潜在变量上的某种推理分布。与典型的潜在变量模型(如变分自编码器 (Rezende 等人, 2014))不同,DDPMs 是用固定的(而非可训练的)推理过程q(x1:T∣x0)q(x_{1:T} \mid x_0)q(x1:T∣x0)进行学习的,并且潜在变量的维度相对较高。例如,Ho 等人 (2020) 考虑了以下由递减序列α1:T∈(0,1]T\alpha_{1:T} \in (0, 1]^Tα1:T∈(0,1]T 参数化的高斯转移马尔可夫链:
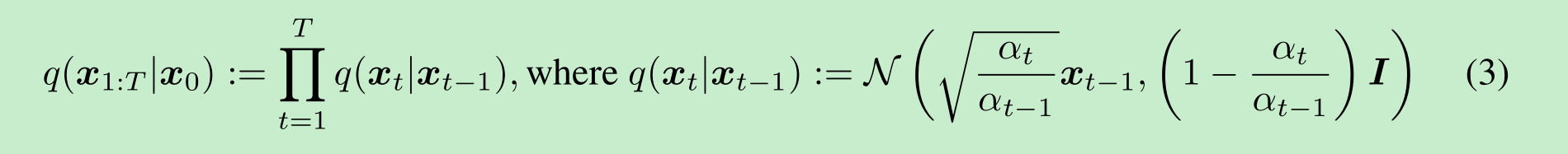
其中(协方差矩阵的设定确保)其对角线上的项为正数。由于采样过程(从x₀到xₜ)具有自回归特性,这一过程被称为前向过程。我们将潜在变量模型pθ(x₀:T)(这是一个从xₜ到x₀进行采样的马尔可夫链)称为生成过程,因为它近似于难以处理(无法直接计算)的逆向过程q(xₜ₋₁|xₜ)。直观地说,前向过程逐步向观测值x₀添加噪声,而生成过程则逐步对含噪观测值进行去噪(如图1左侧所示)。
前向过程的一个特殊性质是
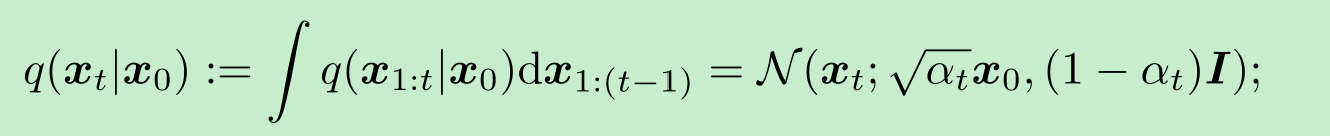
因此,我们可以将 xtx_txt表示为 x0x_0x0和一个噪声变量(设为 ϵ\epsilonϵ)的线性组合:
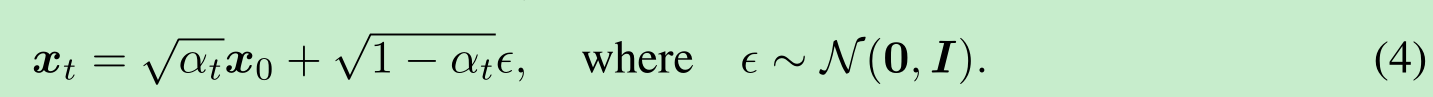
当我们将 αT\alpha_TαT 设置得足够接近0时,对于所有的 x0x_0x0,条件分布q(xT∣x0)q(x_T|x_0)q(xT∣x0)都会收敛到一个标准高斯分布,因此很自然地,我们可以将pθ(xT)p_\theta(x_T)pθ(xT) 设定为 N(0,I)\mathcal{N}(0, I)N(0,I)。如果所有条件分布都被建模为具有可训练均值函数和固定方差的高斯分布,那么公式(2)中的目标函数可以简化为:
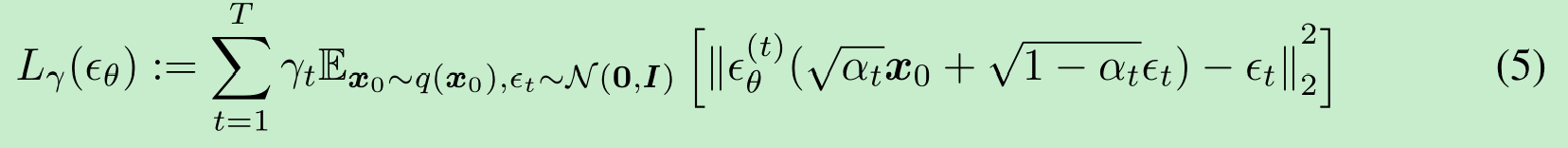
其中,ϵθ:={ϵθ(t)}t=1T\epsilon_\theta := \{\epsilon_\theta^{(t)}\}_{t=1}^Tϵθ:={ϵθ(t)}t=1T是一组TTT 个函数,每个 ϵθ(t):X→X\epsilon_\theta^{(t)}: \mathcal{X} \to \mathcal{X}ϵθ(t):X→X(由 ttt索引)是一个具有可训练参数 θ(t)\theta^{(t)}θ(t)的函数,而γ:=[γ1,…,γT]\gamma := [\gamma_1, \ldots, \gamma_T]γ:=[γ1,…,γT]是一个取决于 α1:T\alpha_{1:T}α1:T的目标函数中的正系数向量。在 Ho 等人(2020)的研究中,当γ=1\gamma = 1γ=1 时,目标函数被优化以最大化训练模型的生成性能;这也是基于分数匹配的噪声条件分数网络(Song & Ermon, 2019)所使用的目标函数(Hyvärinen, 2005; Vincent, 2011)。从训练好的模型中,首先从先验分布 pθ(xT)p_\theta(x_T)pθ(xT) 中采样 xTx_TxT,然后从生成过程中迭代采样 xt−1x_{t-1}xt−1,最终得到 x0x_0x0。
前向过程的长度 TTT 是去噪扩散概率模型(DDPMs)中的一个重要超参数。从变分角度看,较大的 TTT使得逆向过程接近高斯分布(Sohl-Dickstein 等人,2015),因此用高斯条件分布建模的生成过程成为一个良好的近似;这促使选择较大的 TTT值,例如 Ho 等人(2020)中使用的T=1000T = 1000T=1000。然而,由于所有 TTT 次迭代必须按顺序执行(而非并行),为x0x_0x0,从 DDPMs 中采样的速度比从其他深度生成模型中采样要慢得多,这使得 DDPMs 在计算资源有限且延迟敏感的任务中不切实际。
针对非马尔可夫前向过程的变分推断
由于生成模型近似于推断过程的反向过程,因此我们需要重新思考推断过程,以减少生成模型所需的迭代次数。我们的关键发现是,以 LγL_{\gamma}Lγ 形式呈现的去噪扩散概率模型(DDPM,Denoising Diffusion Probabilistic Models)目标函数仅依赖于边缘分布 q(xt∣x0)q(x_t|x_0)q(xt∣x0),而并不直接依赖于联合分布 q(x1:T∣x0)q(x_{1:T}|x_0)q(x1:T∣x0)。由于具有相同边缘分布的推断分布(联合分布)有很多种,因此我们探索了非马尔可夫的替代推断过程,这催生了新的生成过程(如图1右侧所示)。如下文所示,这些非马尔可夫推断过程得出的替代目标函数与DDPM的目标函数相同。在附录A中,我们表明非马尔可夫视角同样适用于非高斯情形。
3.1 非马尔可夫前向过程
让我们考虑一个由实向量 σ∈R≥0T\sigma \in \mathbb{R}_{\geq 0}^Tσ∈R≥0T 索引的推断分布族 Q\mathcal{Q}Q:
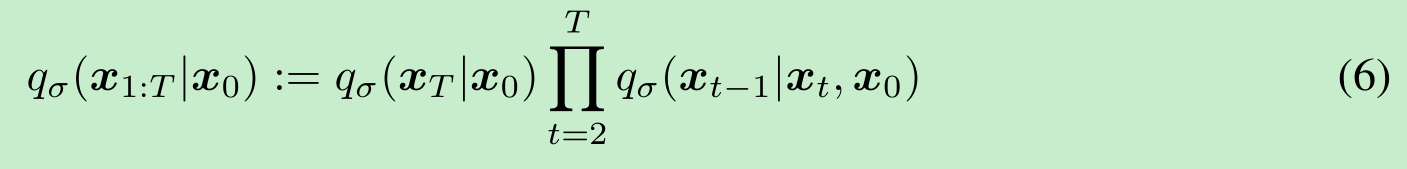
其中 qσ(xT∣x0)=N(αTx0,(1−αT)I)q_{\sigma}(\boldsymbol{x}_T|\boldsymbol{x}_0) = \mathcal{N}(\sqrt{\alpha_T}\boldsymbol{x}_0, (1 - \alpha_T)\boldsymbol{I})qσ(xT∣x0)=N(αTx0,(1−αT)I),并且对于所有 t>1t > 1t>1,
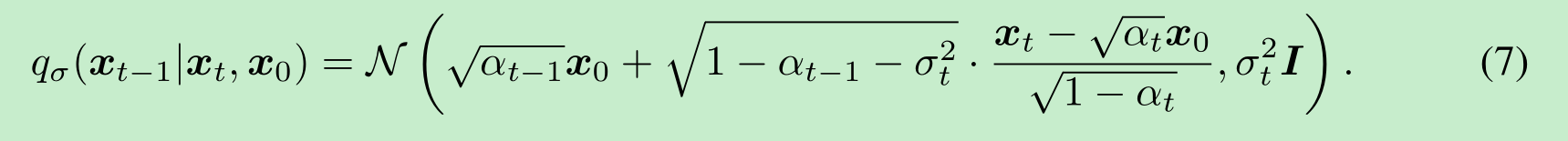
选择均值函数是为了确保对于所有 ttt,qσ(xt∣x0)=N(αtx0,(1−αt)I)q_{\sigma}(\boldsymbol{x}_t|\boldsymbol{x}_0) = \mathcal{N}(\sqrt{\alpha_t}\boldsymbol{x}_0, (1 - \alpha_t)\boldsymbol{I})qσ(xt∣x0)=N(αtx0,(1−αt)I)(见附录B的引理1),从而定义一个联合推断分布,使其如期望的那样匹配“边缘分布”。前向过程可以从贝叶斯规则推导得出:
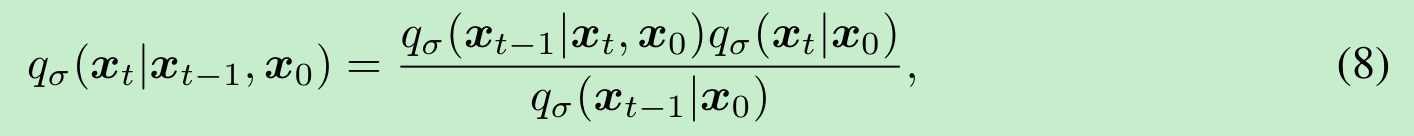
(尽管在本文的其余部分我们并未使用这一事实)它同样服从高斯分布。与公式(3)中的扩散过程不同,此处的前向过程不再是马尔可夫过程,因为每个 xtx_txt 可能同时依赖于 xt−1x_{t-1}xt−1 和 x0x_0x0。参数 σ\sigmaσ 的大小控制着前向过程的随机性程度;当 σ→0\sigma \to 0σ→0 时,我们达到一种极端情况,即只要我们观察到某个 ttt 时刻的 x0x_0x0 和 xtx_txt,那么 xt−1x_{t-1}xt−1 就会变得已知且固定。
3.2 生成过程与统一的变分推断目标
接下来,我们定义一个可训练的生成过程 pθ(x0:T)p_{\theta}(\boldsymbol{x}_{0:T})pθ(x0:T),其中每个 pθ(t)(xt−1∣xt)p_{\theta}^{(t)}(\boldsymbol{x}_{t - 1}|\boldsymbol{x}_t)pθ(t)(xt−1∣xt) 利用了 qσ(xt−1∣xt,x0)q_{\sigma}(\boldsymbol{x}_{t - 1}|\boldsymbol{x}_t, \boldsymbol{x}_0)qσ(xt−1∣xt,x0) 的知识。直观地说,给定一个含噪观测值 xt\boldsymbol{x}_txt,我们首先对相应的 x0\boldsymbol{x}_0x0 进行预测,然后通过之前定义的反向条件分布 qσ(xt−1∣xt,x0)q_{\sigma}(\boldsymbol{x}_{t - 1}|\boldsymbol{x}_t, \boldsymbol{x}_0)qσ(xt−1∣xt,x0) 得到一个样本 xt−1\boldsymbol{x}_{t - 1}xt−1。
对于某些 x0∼q(x0)\boldsymbol{x}_0 \sim q(\boldsymbol{x}_0)x0∼q(x0) 和 ϵt∼N(0,I)\epsilon_t \sim \mathcal{N}(\boldsymbol{0}, \boldsymbol{I})ϵt∼N(0,I),xt\boldsymbol{x}_txt 可以通过公式(4)得到。模型 ϵθ(t)(xt)\epsilon_{\theta}^{(t)}(\boldsymbol{x}_t)ϵθ(t)(xt) 然后在不知道 x0\boldsymbol{x}_0x0 的情况下,尝试从 xt\boldsymbol{x}_txt 预测 ϵt\epsilon_tϵt。通过重写公式(4),我们可以预测去噪后的观测值,即在给定 xt\boldsymbol{x}_txt 的情况下对 x0\boldsymbol{x}_0x0 的预测:
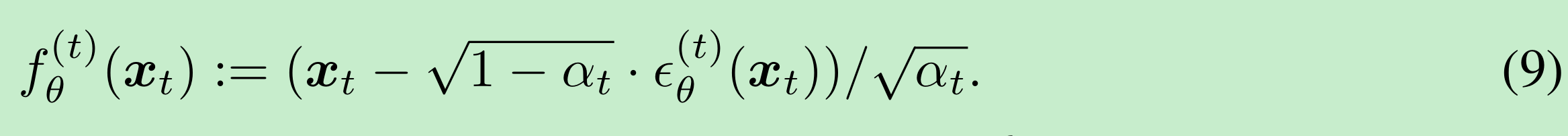
然后,我们可以定义一个固定先验 pθ(xT)=N(0,I)p_{\theta}(\boldsymbol{x}_T) = \mathcal{N}(\boldsymbol{0}, \boldsymbol{I})pθ(xT)=N(0,I) 的生成过程,以及
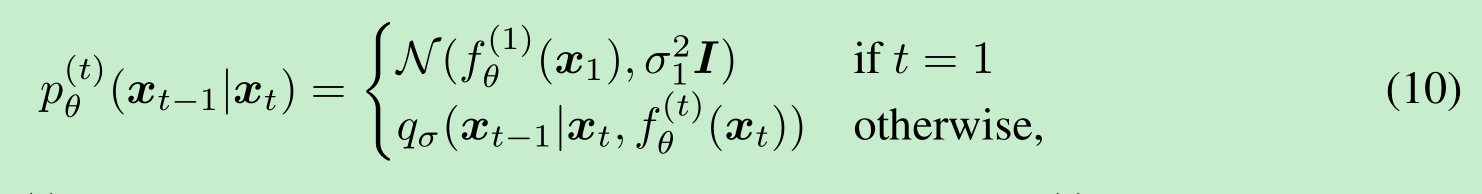
其中 qσ(xt−1∣xt,fθ(t)(xt))q_{\sigma}(\boldsymbol{x}_{t - 1}|\boldsymbol{x}_t, f_{\theta}^{(t)}(\boldsymbol{x}_t))qσ(xt−1∣xt,fθ(t)(xt)) 如公式(7)中定义,只是将 x0\boldsymbol{x}_0x0 替换为 fθ(t)(xt)f_{\theta}^{(t)}(\boldsymbol{x}_t)fθ(t)(xt)。为了确保生成过程在所有情况下都适用,我们在 t=1t = 1t=1 的情况下添加了一些高斯噪声(协方差为 σ12I\sigma_1^2\boldsymbol{I}σ12I)。
我们通过以下变分推断目标(它是关于 ϵθ\epsilon_{\theta}ϵθ 的函数)来优化 θ\thetaθ:
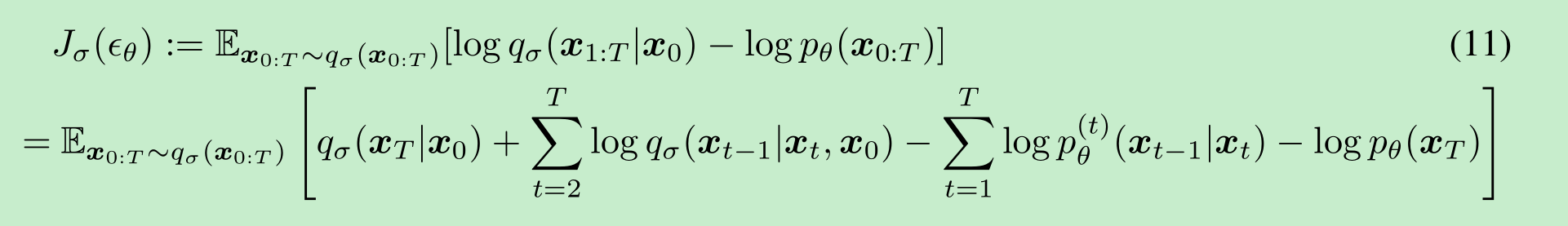
其中我们根据公式(6)对 qσ(x1:T∣x0)q_{\sigma}(\boldsymbol{x}_{1:T}|\boldsymbol{x}_0)qσ(x1:T∣x0) 进行分解,并根据公式(1)对 pθ(x0:T)p_{\theta}(\boldsymbol{x}_{0:T})pθ(x0:T) 进行分解。
从 JσJ_{\sigma}Jσ 的定义来看,对于 σ\sigmaσ 的每一个选择,似乎都需要训练一个不同的模型,因为它对应于不同的变分目标(以及不同的生成过程)。然而,如我们下面所示,对于某些权重 γ\gammaγ,JσJ_{\sigma}Jσ 等价于 LγL_{\gamma}Lγ。
定理1:对于所有 σ>0\sigma > 0σ>0,存在 γ∈R≥0T\gamma \in \mathbb{R}_{\geq 0}^Tγ∈R≥0T 和 C∈RC \in \mathbb{R}C∈R,使得 Jσ=Lγ+CJ_{\sigma} = L_{\gamma} + CJσ=Lγ+C。
变分目标 LγL_{\gamma}Lγ 的特殊性在于,如果模型 ϵθ(t)\epsilon_{\theta}^{(t)}ϵθ(t) 的参数 θ\thetaθ 在不同的 ttt 之间不共享,那么 ϵθ\epsilon_{\theta}ϵθ 的最优解将不依赖于权重 γ\gammaγ(因为全局最优解是通过对求和中的每一项分别最大化得到的)。LγL_{\gamma}Lγ 的这一性质有两个影响。一方面,这为在去噪扩散概率模型(DDPMs)中使用 L1L_1L1 作为变分下界的替代目标函数提供了理由;另一方面,根据定理1,JσJ_{\sigma}Jσ 等价于某个 LγL_{\gamma}Lγ,JσJ_{\sigma}Jσ 的最优解与 L1L_1L1 的最优解相同。因此,如果模型 ϵθ\epsilon_{\theta}ϵθ 中的参数在不同的 ttt 之间不共享,那么Ho等人(2020)中使用的 L1L_1L1 目标也可以用作变分 JσJ_{\sigma}Jσ 的替代目标。
从广义生成过程中采样
以 L1L_1L1 为目标函数时,我们不仅在学习 Sohl-Dickstein 等人(2015 年)以及 Ho 等人(2020 年)所研究的马尔可夫推断过程对应的生成过程,同时也在学习由我们前文所述、以 σ\sigmaσ 为参数的众多非马尔可夫前向过程对应的生成过程。因此,我们基本上可以将预训练的去噪扩散概率模型(DDPM)模型作为新目标函数的解,并通过调整 σ\sigmaσ 来重点寻找一个更能满足我们需求、更擅长生成样本的生成过程。
4.1 去噪扩散隐式模型
根据公式(10)中的 pθ(x1:T)p_{\theta}(\boldsymbol{x}_{1:T})pθ(x1:T),可以通过以下方式从样本 xt\boldsymbol{x}_txt 生成样本 xt−1\boldsymbol{x}_{t - 1}xt−1:
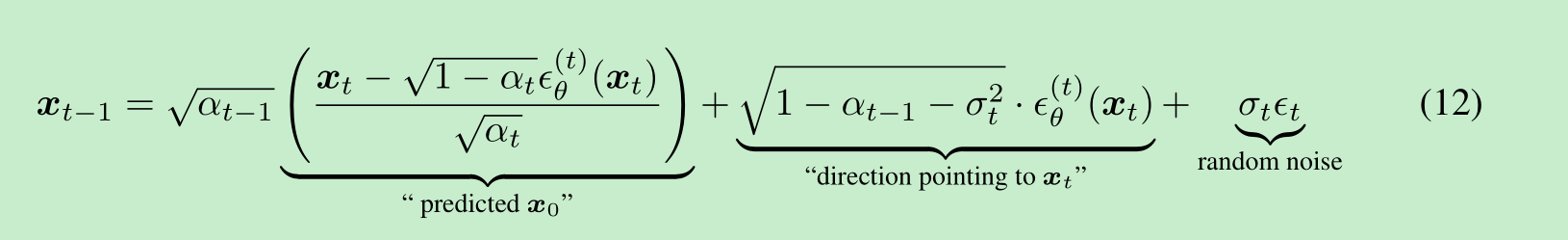
其中 ϵt∼N(0,I)\epsilon_t \sim \mathcal{N}(\boldsymbol{0}, \boldsymbol{I})ϵt∼N(0,I) 是独立于 xt\boldsymbol{x}_txt 的标准高斯噪声,我们定义 α0:=1\alpha_0 := 1α0:=1。不同的 σ\sigmaσ 值选择会得到不同的生成过程,但都使用相同的模型 ϵθ\epsilon_{\theta}ϵθ,因此无需重新训练模型。当对于所有 ttt,σt=(1−αt−1)/(1−αt)1−αt/αt−1\sigma_t = \sqrt{(1 - \alpha_{t - 1}) / (1 - \alpha_t)} \sqrt{1 - \alpha_t / \alpha_{t - 1}}σt=(1−αt−1)/(1−αt)1−αt/αt−1时,前向过程变为马尔可夫过程,生成过程则成为去噪扩散概率模型(DDPM)。
我们注意到另一种特殊情况,即对于所有 ttt,σt=0\sigma_t = 0σt=0;除了 t=1t = 1t=1 的情况外,给定 xt−1\boldsymbol{x}_{t - 1}xt−1 和 x0\boldsymbol{x}_0x0,前向过程变为确定性的。在生成过程中,随机噪声 ϵt\epsilon_tϵt 前的系数变为零。所得模型成为隐式概率模型(Mohamed & Lakshminarayanan, 2016),其中样本是从潜在变量以固定程序(从 xT\boldsymbol{x}_TxT 到 x0\boldsymbol{x}_0x0)生成的。我们将其称为去噪扩散隐式模型(DDIM,发音为 /dɪm/),因为它是一个使用 DDPM 目标进行训练的隐式概率模型(尽管前向过程不再是扩散过程)。
4.2 加速生成过程
在前面的章节中,生成过程被视为反向过程的近似。由于前向过程有 TTT 步,生成过程也被迫采样 TTT 步。然而,只要 qσ(xt∣x0)q_{\sigma}(\boldsymbol{x}_t|\boldsymbol{x}_0)qσ(xt∣x0) 固定,去噪目标 L1L_1L1 并不依赖于特定的前向过程,我们也可以考虑长度小于 TTT 的前向过程,这可以在无需训练不同模型的情况下加速相应的生成过程。
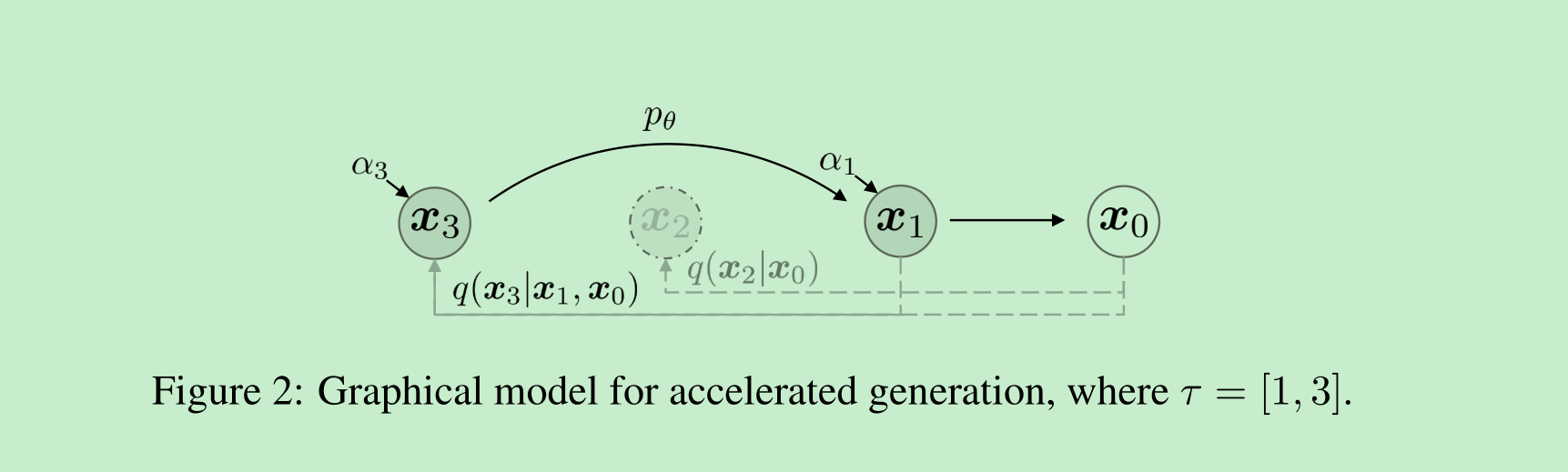
我们将前向过程定义为并非基于所有潜在变量 x1:T\boldsymbol{x}_{1:T}x1:T,而是基于一个子集 {xτ1,…,xτS}\{\boldsymbol{x}_{\tau_1}, \ldots, \boldsymbol{x}_{\tau_S}\}{xτ1,…,xτS},其中 τ\tauτ 是 [1,…,T][1, \ldots, T][1,…,T] 的一个递增子序列,长度为 SSS。特别地,我们定义在 xτ1,…,xτS\boldsymbol{x}_{\tau_1}, \ldots, \boldsymbol{x}_{\tau_S}xτ1,…,xτS 上的顺序前向过程,使得 q(xτi∣x0)=N(ατix0,(1−ατi)I)q(\boldsymbol{x}_{\tau_i}|\boldsymbol{x}_0) = \mathcal{N}(\sqrt{\alpha_{\tau_i}}\boldsymbol{x}_0, (1 - \alpha_{\tau_i})\boldsymbol{I})q(xτi∣x0)=N(ατix0,(1−ατi)I) 与“边缘分布”相匹配(见图2的说明)。生成过程现在根据 reversed(τ)\text{reversed}(\tau)reversed(τ) 对潜在变量进行采样,我们称之为(采样)轨迹。当采样轨迹的长度远小于 TTT 时,由于采样过程的迭代性质,我们可以在计算效率上实现显著提升。
使用与第3节类似的论证,我们可以合理使用用 L1L_1L1 目标训练的模型,因此在训练中无需进行任何更改。我们表明,只需对公式(12)中的更新进行微小更改,即可获得新的、更快的生成过程,这适用于去噪扩散概率模型(DDPM)、去噪扩散隐式模型(DDIM)以及公式(10)中考虑的所有生成过程。我们在附录C.1中包含了这些细节。
原则上,这意味着我们可以训练一个具有任意数量前向步骤的模型,但在生成过程中仅从中采样一些步骤。因此,训练好的模型可以考虑比(Ho等人,2020)中考虑的更多的步骤,甚至可以考虑连续时间变量 ttt(Chen等人,2020)。我们将这方面的实证研究留作未来的工作。
4.3 与神经常微分方程的相关性
此外,我们可以根据公式(12)改写去噪扩散隐式模型(DDIM)的迭代式,其与用于求解常微分方程(ODEs)的欧拉积分法的相似性变得更加明显:
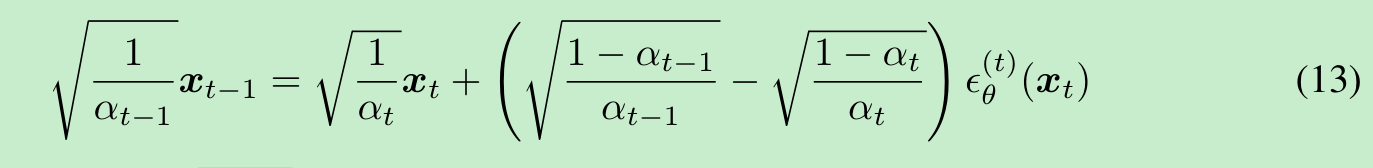
我们可以用 λ\lambdaλ 重新参数化 (1−α/α)(\sqrt{1 - \alpha} / \sqrt{\alpha})(1−α/α),用 H(λ)H(\lambda)H(λ) 重新参数化 (x/α)(\boldsymbol{x} / \sqrt{\alpha})(x/α),然后使用公式(13)对 x0\boldsymbol{x}_0x0 进行采样,这可以被视为对以下常微分方程的积分:
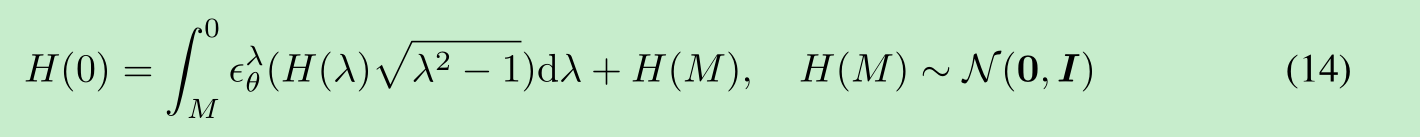
对于非常大的 MMM(对应于 α≈0\alpha \approx 0α≈0 的情况)。这表明,当离散化步数 TTT 足够多时,我们还可以逆转生成过程(从 t=0t = 0t=0 到 t=Tt = Tt=T),该过程将 x0\boldsymbol{x}_0x0 编码为 xT\boldsymbol{x}_TxT,并模拟公式(14)中常微分方程的反向过程。这表明,与去噪扩散概率模型(DDPM)不同,我们可以使用去噪扩散隐式模型(DDIM)获得观测值的编码(以 xT\boldsymbol{x}_TxT 的形式),这对于其他需要模型潜在表示的下游应用可能很有用。
实验
在本节中,我们表明,当考虑较少的迭代次数时,去噪扩散隐式模型(DDIMs)在图像生成方面优于去噪扩散概率模型(DDPMs),相比原始的DDPM生成过程,速度可提升10倍到100倍。此外,与DDPMs不同,一旦初始潜在变量xT\boldsymbol{x}_TxT固定,DDIMs无论生成轨迹如何,都能保留高水平的图像特征,因此它们能够直接从潜在空间进行插值。DDIMs还可用于对样本进行编码,以便从潜在编码中重建样本,而由于随机采样过程,DDPMs无法做到这一点。
对于每个数据集,我们使用相同的训练模型,其中T=1000T = 1000T=1000,目标函数为公式(5)中的LγL_{\gamma}Lγ且γ=1\gamma = 1γ=1;正如我们在第3节中所论述的,训练过程无需进行任何更改。我们唯一做出的改变是如何从模型中生成样本;我们通过控制τ\tauτ(控制样本获取的速度)和σ\sigmaσ(在确定性DDIM和随机DDPM之间进行插值)来实现这一点。
我们考虑[1,…,T][1, \ldots, T][1,…,T]的不同子序列τ\tauτ以及由τ\tauτ的元素索引的不同方差超参数σ\sigmaσ。为了简化比较,我们考虑如下形式的σ\sigmaσ:
στi(η)=η(1−ατi−1)/(1−ατi)1−ατi/ατi−1,(15)
\sigma_{\tau_i}(\eta) = \eta \sqrt{(1 - \alpha_{\tau_{i - 1}}) / (1 - \alpha_{\tau_i})} \sqrt{1 - \alpha_{\tau_i} / \alpha_{\tau_{i - 1}}}, \tag{15}
στi(η)=η(1−ατi−1)/(1−ατi)1−ατi/ατi−1,(15)
其中η∈R≥0\eta \in \mathbb{R}_{\geq 0}η∈R≥0是一个我们可以直接控制的超参数。当η=1\eta = 1η=1时,这包括原始的DDPM生成过程;当η=0\eta = 0η=0时,则为DDIM。我们还考虑随机噪声标准差大于σ(1)\sigma(1)σ(1)的DDPM,我们将其表示为σ^\hat{\sigma}σ^:σ^τi=1−ατi/ατi−1\hat{\sigma}_{\tau_i} = \sqrt{1 - \alpha_{\tau_i} / \alpha_{\tau_{i - 1}}}σ^τi=1−ατi/ατi−1。Ho等人(2020)中的实现仅使用此来获取CIFAR10样本,但不获取其他数据集的样本。我们在附录D中包含了更多细节。
5.1 样本质量与效率
在表1中,我们报告了使用在CIFAR10和CelebA上训练的模型生成的样本质量,使用弗雷歇初始距离(FID,Heusel等人,2017)进行衡量,其中我们改变了生成样本所用的时间步数(dim(τ)\text{dim}(\tau)dim(τ))以及过程的随机性(η\etaη)。正如预期的那样,随着dim(τ)\text{dim}(\tau)dim(τ)的增加,样本质量提高,这体现了样本质量与计算成本之间的权衡。我们观察到,当dim(τ)\text{dim}(\tau)dim(τ)较小时,去噪扩散隐式模型(DDIM,η=0\eta = 0η=0)达到了最佳的样本质量,而与具有相同dim(τ)\text{dim}(\tau)dim(τ)但随机性较低的模型相比,去噪扩散概率模型(DDPM,η=1\eta = 1η=1和σ^\hat{\sigma}σ^)的样本质量通常较差,但在Ho等人(2020)报告的dim(τ)=1000\text{dim}(\tau) = 1000dim(τ)=1000和σ^\hat{\sigma}σ^的情况下,DDIM的表现略差。然而,对于较小的dim(τ)\text{dim}(\tau)dim(τ),σ^\hat{\sigma}σ^的样本质量会变得更差,这表明它不适合较短的轨迹。另一方面,DDIM更稳定地实现了高样本质量。
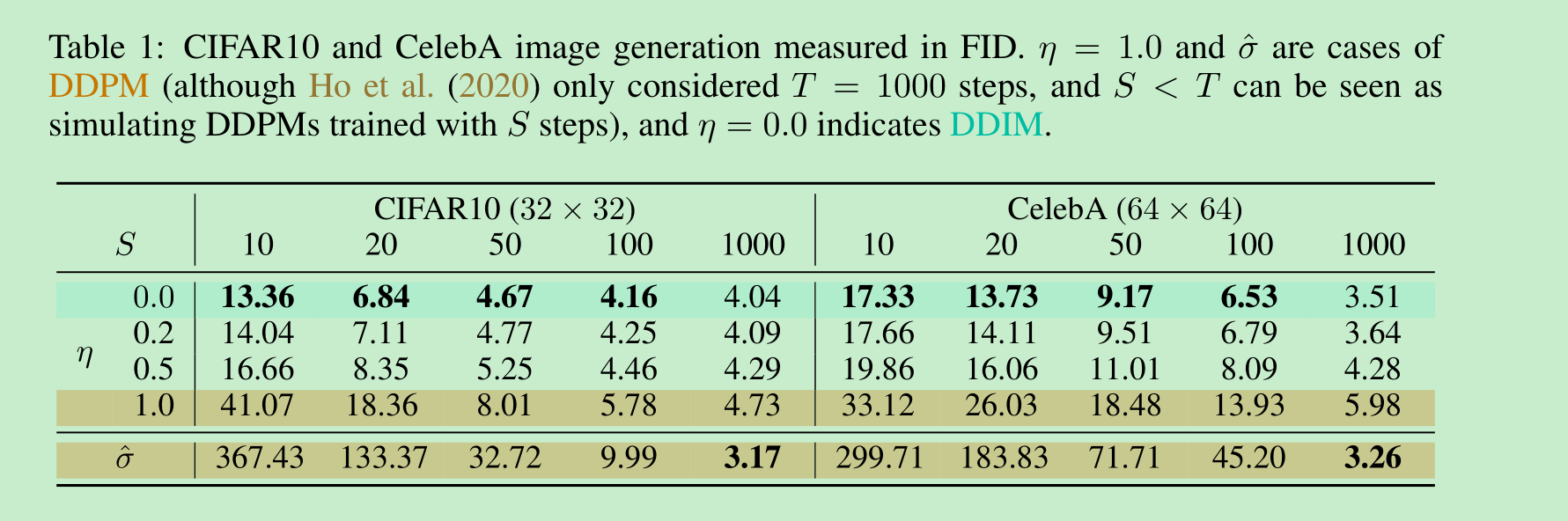
在图3中,我们展示了在采样步数相同但 σ\sigmaσ 不同的情况下,CIFAR10和CelebA数据集的样本。对于去噪扩散概率模型(DDPM),当采样轨迹为10步时,样本质量迅速下降。对于使用 σ^\hat{\sigma}σ^ 的情况,在短轨迹下生成的图像似乎带有更多噪声干扰;这就解释了为什么其弗雷歇初始距离(FID)分数比其他方法差得多,因为FID对此类干扰非常敏感(如Jolicoeur-Martineau等人(2020)所讨论的)。
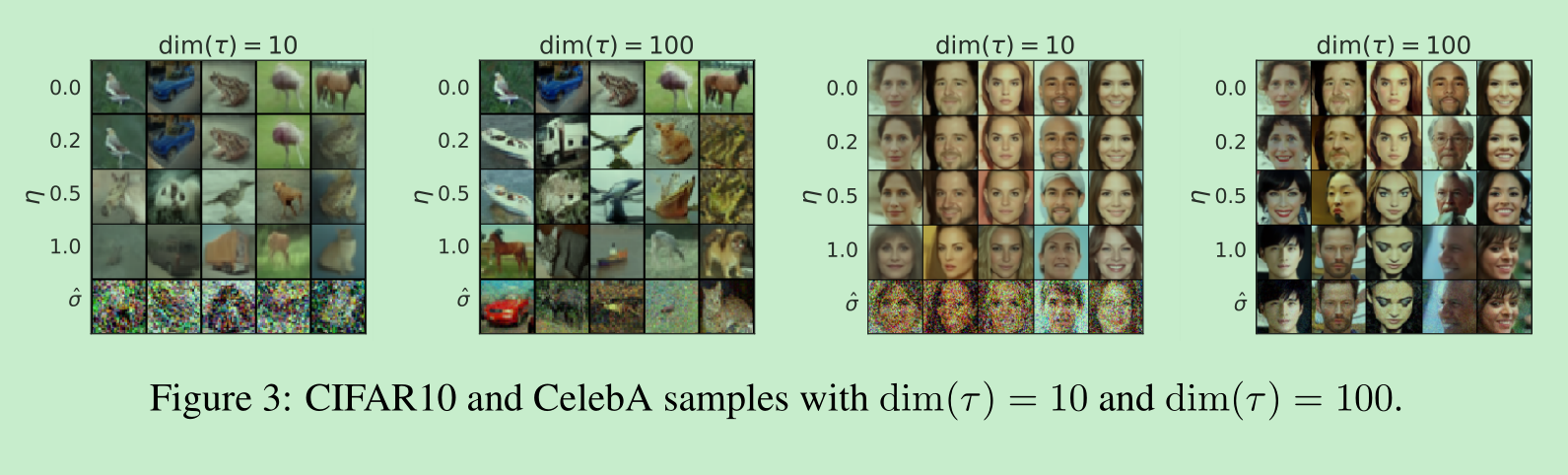
在图4中,我们展示生成一个样本所需的时间与样本轨迹的长度呈线性关系。这表明去噪扩散隐式模型(DDIM)在更高效地生成样本方面很有用,因为样本可以在更少的步骤中生成。值得注意的是,DDIM能够在20到100步内生成质量与1000步模型相当的样本,与原始的去噪扩散概率模型(DDPM)相比,速度提升了10到50倍。尽管DDPM在100步时也能达到合理的样本质量,但DDIM实现这一点所需的步骤要少得多;在CelebA数据集上,100步DDPM的弗雷歇初始距离(FID)分数与20步DDIM的FID分数相似。
5.2 去噪扩散隐式模型(DDIM)中样本的一致性
对于去噪扩散隐式模型(DDIM),生成过程是确定性的,并且 x0\boldsymbol{x}_0x0 仅取决于初始状态 xT\boldsymbol{x}_TxT。在图5中,我们从相同的初始 xT\boldsymbol{x}_TxT 开始,观察在不同生成轨迹(即不同的 τ\tauτ)下生成的图像。有趣的是,对于具有相同初始 xT\boldsymbol{x}_TxT 的生成图像,大多数高级特征是相似的,而与生成轨迹无关。在许多情况下,仅用20步生成的样本在高级特征方面已经与用1000步生成的样本非常相似,仅在细节上有微小差异。因此,似乎仅 xT\boldsymbol{x}_TxT 就能对图像进行信息丰富的潜在编码;而影响样本质量的细微细节则编码在参数中,因为更长的样本轨迹会给出更高质量的样本,但不会显著影响高级特征。我们在附录D.4中展示了更多样本。

5.3 确定性生成过程中的插值

由于去噪扩散隐式模型(DDIM)样本的高级特征由 xT\boldsymbol{x}_TxT 编码,我们有兴趣了解它是否会表现出与其他隐式概率模型(如生成对抗网络(GANs, Goodfellow等人,2014))中观察到的类似的语义插值效果。这与Ho等人(2020)中的插值过程不同,因为在去噪扩散概率模型(DDPM)中,由于生成过程的随机性,相同的 xT\boldsymbol{x}_TxT 会导致高度多样化的 x0\boldsymbol{x}_0x0 。在图6中,我们展示了 xT\boldsymbol{x}_TxT 中的简单插值可以在两个样本之间产生语义上有意义的插值。我们在附录D.5中提供了更多细节和样本。这使得DDIM能够直接通过潜在变量在高级层面上控制生成的图像,而DDPM无法做到这一点。
5.4 从潜在空间重建
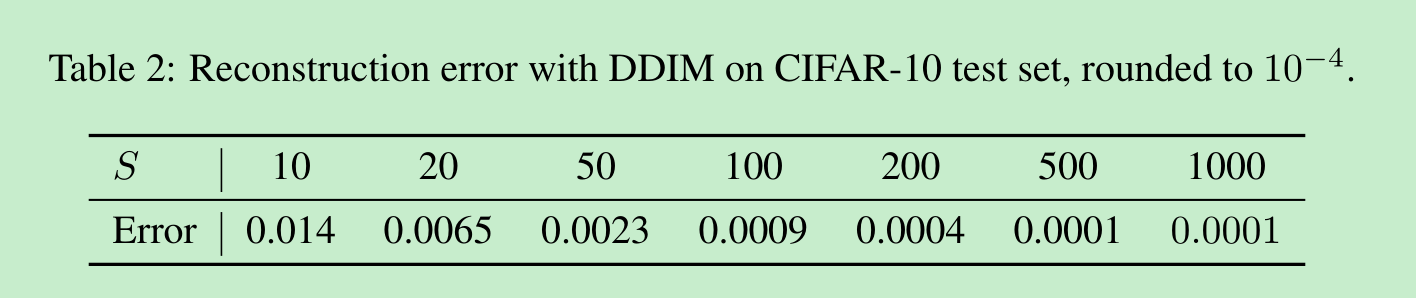
由于去噪扩散隐式模型(DDIM)是特定常微分方程(ODE)的欧拉积分,因此观察它是否能够将 x0\boldsymbol{x}_0x0 编码为 xT\boldsymbol{x}_TxT(即公式(14)的逆向过程),并从得到的 xT\boldsymbol{x}_TxT 重建 x0\boldsymbol{x}_0x0(即公式(14)的正向过程)将是一件有趣的事情。我们考虑在CIFAR-10测试集上使用CIFAR-10模型进行编码和解码,编码和解码均使用 SSS 步;我们在表2中报告了(缩放到[0, 1]范围内的)每维均方误差。我们的结果表明,对于更大的 SSS 值,DDIM的重构误差更低,并且具有与神经常微分方程(Neural ODEs)和标准化流(normalizing flows)类似的特性。由于DDPM具有随机性,因此对于DDPM不能得出同样的结论。
6 相关工作
我们的工作基于一大类现有的将生成模型作为马尔可夫链的转移算子来学习的方法(Sohl-Dickstein等人,2015;Bengio等人,2014;Salimans等人,2014;Song等人,2017;Goyal等人,2017;Levy等人,2017)。其中,去噪扩散概率模型(DDPMs,Ho等人(2020))和噪声条件得分网络(NCSNs,Song & Ermon(2019;2020))最近取得了可与生成对抗网络(GANs,Brock等人,2018;Karras等人,2018)相媲美的高样本质量。DDPMs优化对数似然的变分下界,而NCSNs优化数据在非参数帕累托密度估计器上的得分匹配目标(Hyvärinen,2005)(Vincent,2011;Raphan & Simoncelli,2011)。
尽管动机不同,DDPMs和NCSNs密切相关。两者在许多噪声水平下都使用去噪自编码器目标,并且都使用类似于朗之万动力学的过程来生成样本(Neal等人,2011)。由于朗之万动力学是梯度流的离散化(Jordan等人,1998),DDPM和NCSN都需要许多步骤才能实现良好的样本质量。这与观察结果一致,即DDPM和现有的NCSN方法在几次迭代中生成高质量样本存在困难。
另一方面,去噪扩散隐式模型(DDIM)是一种隐式生成模型(Mohamed & Lakshminarayanan,2016),其中样本由潜在变量唯一确定。因此,DDIM具有类似于GANs(Goodfellow等人,2014)和可逆流(Dinh等人,2016)的某些特性,例如产生语义上有意义的插值的能力。我们从纯变分的角度推导出DDIM,其中朗之万动力学的限制不相关;这可以部分解释为什么在更少的迭代次数下,我们能够观察到比DDPM更优越的样本质量。DDIM的采样过程也让人联想到具有连续深度的神经网络(Chen等人,2018;Grathwohl等人,2018),因为它从相同潜在变量生成的样本具有相似的高级视觉特征,而与具体的采样轨迹无关。
