Mamba模型介绍

前言

我们通过Transformer模型的学习可以知道，在最开始处理这个序列数据的时候是通过RNN和CNN来进行处理的，但是RNN由于自己不能够进行并行计算，同时会产生遗忘，所以引入了注意力机制，Transformer的创新就是引入了多头自注意力机制。

而本文所要研究的Mamba模型和Transformer模型一样同样是处理序列数据的。可以利用这个模型处理一串有顺序信息的数据

Mamba基于SSM或S4发展为S6

这些概念不需要知道特别清楚，只需要知道

• SSM 是 State Space Model（状态空间模型）的缩写
• S4 是 SSM 的一种改进版
• Mamba 又是 S4 的升级版，作者把它叫 S6（Selective SSM）
• 它们就像“祖孙三代”：SSM → S4 → S6（Mamba）。

Transformer模型有一个缺点

Transformer模型在处理特别长的文本时，计算量会爆炸。

• 这是因为由于注意力机制，Transformer模型在读取句子中的单词的时候，会把这个单词的前面的词在扫一遍。才能决定下一个字最该说什么。

• 今天天气真好，我们一起去郊游吧。

  • 生成“真”时，要回看“今、天、天、气”；
  • 生成“好”时，要回看“今、天、天、气、真”；

• 为了得到下一个字的表示，要把当前这个字的 Query，与前面所有字的 Key 做点积，算出“谁重要”，再把对应的 Value 加权求和。

• 用公式写就是Attention(Q, K, V) = softmax(Q·Kᵀ / √d) · V

几种模型的对比

• RNN：像“递纸条”，每一步只把当前字的信息写到隐藏状态里，然后把这个隐藏状态传下一步。计算量只和 L 成正比，但缺点是难以捕捉长距离关系
• Transformer：像“全班开大会”，每一步都要把前面所有同学的发言再听一遍，信息完整但时间、空间都是 L²
• Mamba：像“聪明的秘书”，把前面所有内容压缩成一份“摘要”，再决定哪些信息要留、哪些要丢，既保留长距离记忆，又保持线性复杂度 O(L)

状态空间和SSM

状态向量和状态空间：举个例子来理解
1.想象春游，路线是固定的5个站点，学校门口->公交站->公园门口->湖边->山顶
2.每个站点上都会有一个牌子，包含信息：1. 山顶还有几公里 2. 当前海拔多少米 3. 累不累（体力值 0~100)
3.比如公园的牌子写：离山顶 2 km，海拔 50 m，体力值 70将其写为一排[2, 50, 70]，这个就是一个状态向量。
4.当走路的时候这三个变量发生变化，状态向量完成更新
5.如果把 5 个站点 × 各种可能的体力值都列出来，就得到一大堆向量，这一大堆向量就称为状态空间。

将春游换成我们的自然语言处理：
我们处理这句话“I want to order a hamburger.”
读完 “I” → [主语=I, 单复数=单, 时态=现在, …]
读完 “want” → [主语=I, 动词=want, 单复数=单, …]
读完 “order” → [主语=I, 动词=want, 动作=order, …]
向量里的数字在变，每读一个词→ 状态向量更新一次，所有可能出现的向量 → 构成“状态空间，
模型就是根据当前这排数字，猜下一个词该谁上场

那么如何来表示下一步可能去哪里呢，以及哪些变化会将你带到下一个状态呢。
下一步去哪里，并不是由状态向量决定的，而是由当前的状态向量与系统中存好的地图A和B矩阵来决定的。
状态更新方程。$h_{next}=A\cdot h_{now}+B\cdot x_{input}$
A和B就是地图矩阵。其实A就是存储着之前所有历史信息的浓缩精华(可以通过一系列系数组成的矩阵表示之)，以基于A更新下一个时刻的空间状态hidden state
这个$x_{input}$就是可能的变化，可能是向左，可能是向右。这个也是矩阵。
往左往右这个动作$x_{input}$与固定矩阵 B 相乘，就直接把书包里的数字改成下一种合法状态
下一步去哪儿是由固定地图（A、B）+ 当前书包（ℎ）+ 你选择的动作$x_{input}$共同算出

地图从哪里来
这个就属于预训练权重的概念，官方或社区把训练好的 A、B、C、D 打包成 .pt、.safetensors 等文件放到 GitHub / Hugging Face

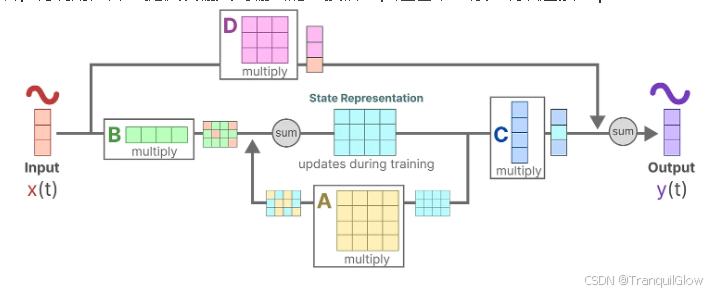
SSM的状态方程
• 状态方程：h′(t) = A·h(t) + B·x(t)
• 输出方程：y(t) = C·h(t) + D·x(t)

从SSM到S4，S4D的升级之路

总共需要6步升级
1.离散化SSM
2.循环表示
3.卷积表示
4.基于HiPPO处理长序列
5.S4
6.S4D

1.离散化SSM
SSM（State Space Model）原本是为连续信号设计的，比如电压、温度这种随时间平滑变化的物理量。
但是做NLP的时候，输入是离散的文字序列，必须把离散文字“伪装”成连续信号，才能够使用SSM进行处理。
每个字在自己的时间段里保持恒定值
$x(t)=xk当t\in [k\Delta ,(k+1)\Delta )$，其中$\Delta$是步长。可学习的参数，就像模型自己决定“楼梯多宽
之后我们就可以通过这个SSM状态方程进行激活了。但是SSM 输出的是连续信号 y(t)，但我们最终要的是离散的字向量。所以，我们在每个字的终点时间 (k+1)Δ 处采样一下，得到：$yk=y((k+1)\Delta )$，这样，又变回了我们熟悉的离散序列 [y0, y1, y2, …]。
把文字变成楼梯状的连续信号 → 喂给 SSM 微分方程 → 在关键时间点采样拿回离散输出。

2.循环结构表示：方便快速推理
引入：SSM 吃完楼梯信号后，怎么在“推理（生成）”阶段像 RNN 一样一步只跑一个 token，却跑得飞快。
把连续微分方程“折叠”成 RNN 式递推公式，每一步只依赖上一秒的状态，于是推理时不用看全部历史，省内存、常数时间出结果
连续版 SSM ，要解它，得做“积分”，理论上要从 −∞ 积到当前 t，太慢，之后就是数学推理了，可以暂时不用看。

3.卷积结构表示：方便并行训练
卷积计算就是矩阵计算，讲矩阵拆成一个个的小块。
卷积核 K = [k0, k1, k2, ...] 在计算前就已确定，不依赖任何中间结果。
每个输出位置都是“独立点积”，比如下式，这三个式子没有依赖，可以独立计算。
y0 = x0k0 + x1k1
y1 = x1k0 + x2k1
y2 = x2k0 + x3k1

4.长距离依赖问题的解决之道
为什么RNN会丢失呢，h = tanh(W h + U x)，旧信息被 W h 一遍遍地乘小数 → 梯度消失 → 几百步后≈0。新信息又 把旧位置覆盖掉 → 新的盖旧 → 更远的前文直接消失
把“整个历史”当成一条连续曲线，用一组特殊多项式（Legendre 多项式）去逼近它。只存多项式系数（正好 64 个！）就能近似恢复整条过去曲线，每来一个新点，只改系数，不改曲线形状 → 旧信息不会被清零

模型	记忆机制	远记忆存活	内存	并行
普通 RNN	直接覆写	❌ 几百步后≈0	O(N)	❌
LSTM	门控遗忘	✅ 但梯度难穿千步	O(N)	❌
SSM+HiPPO	多项式系数	✅ 千~万步仍可用	O(N)	✅ 卷积模式

1. HiPPO 把“全部历史”当成连续曲线，用 64 个多项式系数存成“缩略图” 。
2. 矩阵 A 是数学家算好的“最优更新规则”：新信息加进来，旧信息指数衰减但永不清零。
3. 因此 SSM 能像 Transformer 一样记得超远，又像 RNN 一样只存固定内存。