当前位置： 首页 > news >正文

【卷积神经网络详解与实例】6——经典CNN之LeNet

news 2025/9/13 13:26:37

1、Lenet

1.1 开发背景

本节将介绍LeNet，它是最早发布的卷积神经网络之一，也是将深度学习推向繁荣的一座里程碑，因其在计算机视觉任务中的高效性能而受到广泛关注。

Lenet 是一系列网络的合称，包括 Lenet1 - Lenet5，由 Yann LeCun （以其命名）等人在论文《Handwritten Digit Recognition with a Back-Propagation Network》中提出，目的是识别手写数字。当时，LeNet取得了与支持向量机（support vector machines）性能相媲美的成果，成为监督学习的主流方法。

LeNet首次采用了卷积层、池化层这两个全新的神经网络组件，接收灰度图像，并输出其中包含的手写数字，在手写字符识别任务上取得了瞩目的准确率。LeNet网络的一系列的版本，以LeNet-5版本最为著名，也是LeNet系列中效果最佳的版本。

1.2 网络架构

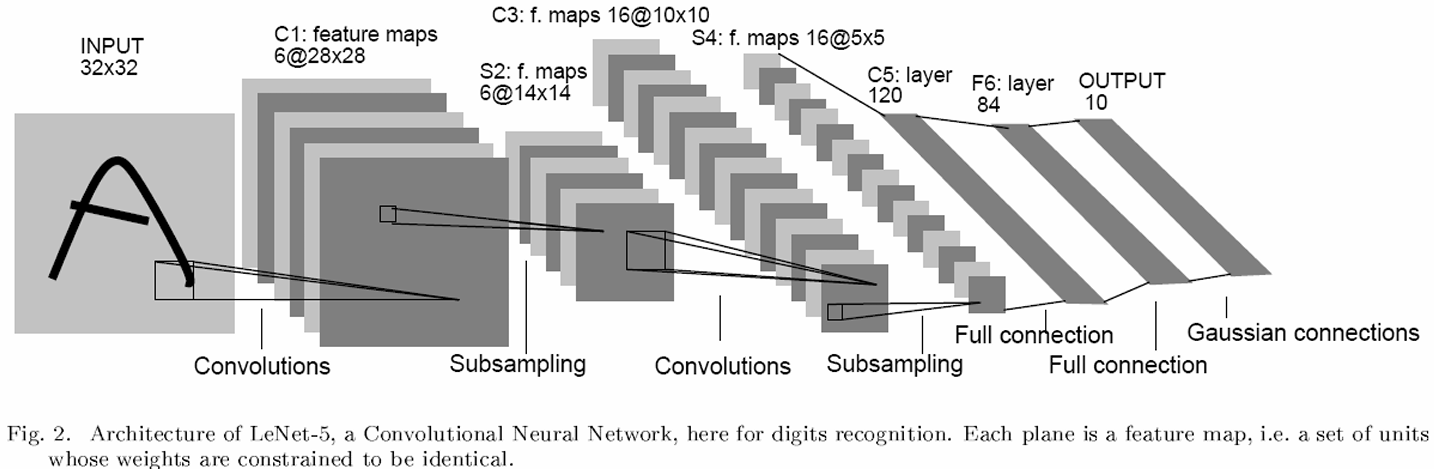
LeNet5网络总共有六层网络（不包含输入输出层的话）：C1, S2, C3, S4, C5, F6。

1.2.1 第一层——卷积层C1

卷积计算详解可以参考以下文章：

【卷积神经网络详解与实例】2——卷积计算详解_卷积运算过程示意图-CSDN博客https://blog.csdn.net/colus_SEU/article/details/150657893?spm=1001.2014.3001.5501

1.2.1.1 具体参数

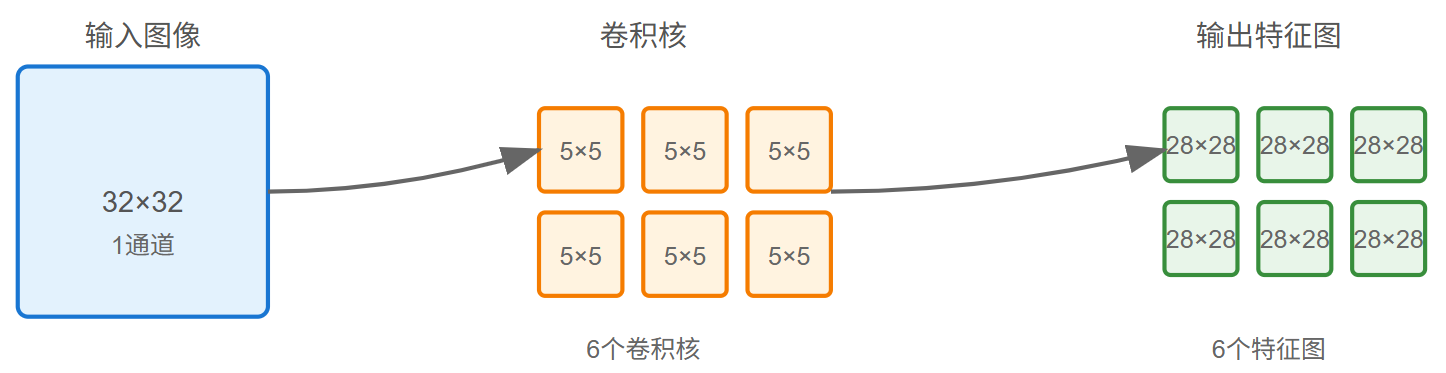
  • 输入图像的大小为 32×32

  • 卷积核kernel size的大小为 5×5

  • 卷积核数量为 6 个

  • 输出featuremap大小：28×28 （28通过32-5+1计算得到）

  • 神经元数量：28×28×6

  • 训练参数：（5×5+1)×6=156 由于参数（权值）共享的原因，对于同个卷积核每个神经元均使用相同的参数，因此，参数个数为（5×5+1）×6= 156，其中5×5为卷积核参数，1为偏置参数.

  • 连接数：训练参数×输出featuremap大小=（5×5+1）×6×28×28=122304

1.2.1.2 卷积的作用

  • 通过卷积运算，可以使原信号特征增强，降低噪音。在图像上卷积之后主要是减少图像噪声，提取图像的特征。

  • 卷积网络能很好地适应图像的平移不变性：例如稍稍移动一幅猫的图像，它仍然是一幅猫的图像。

  • 卷积操作保留了图像块之间的空间信息，进行卷积操作的图像块之间的相对位置关系没有改变。

图像在不同卷积核上进行卷积之后的效果图如下：

图中的图像处理操作名称具体有：Identity（恒等变换）、Edge detection（边缘检测）、Sharpen（锐化）、Box blur (normalized)（归一化盒式模糊）、Gaussian blur (approximation)（高斯模糊近似）。

1.2.2 第二层——池化层C2（下采样）

池化操作详解可以参考一下文章：

【卷积神经网络详解与实例】3——池化与反池化操作-CSDN博客https://blog.csdn.net/colus_SEU/article/details/151370006?spm=1001.2014.3001.5501

1.2.2.1 具体参数

在现代架构中，池化层是没有参数的，这涉及到历史和现实的区别，下文会提到。

  • 池化层的输入大小：28×28

  • 池化大小：2×2

  • 池化层数：6

  • 输出featureMap大小：14×14

  • 神经元数量：14×14×6

  • 训练参数：2×6（每个池化层有两个可训练的参数）

  • 连接数：（2×2+1）×6×14×14

1.2.2.2 池化层的作用

池化层的作用是对输入特征图进行下采样（Subsampling），从而降低数据的空间维度（高度和宽度），也叫特征映射（特征降维）。

如果池化单元为2×2，且池化单元之间没有重叠，则6个特征图的大小经池化后从28×28变为14×14。

这样操作的好处在于：

  • 减少计算量：减少了后续层的参数和计算复杂度。

  • 引入平移不变性：使网络对输入图像中特征的微小位置变化不那么敏感。

  • 控制过拟合：通过减少参数数量间接起到防止过拟合的作用。

1.2.2.3 池化层的计算

在Yann LeCun 1998年的原始论文《Gradient-Based Learning Applied to Document Recognition》中的描述如下：

  • 具体结构：在最初的LeNet-5中，池化层被称为“子采样层”（Subsampling Layer）。每个池化窗口的大小是2x2，步长（stride）为2，因此输出特征图的大小会减半。

  • 操作：它对2x2窗口内的4个值求和后乘以一个可训练的系数，再加上一个可训练的偏置，最后通过一个Sigmoid激活函数。 用公式表示就是：

    output = \text{Sigmoid}\left(w \cdot \sum_{i=1}^{4} input_i + b\right)

     

    其中 w 是权重系数，b 是偏置。

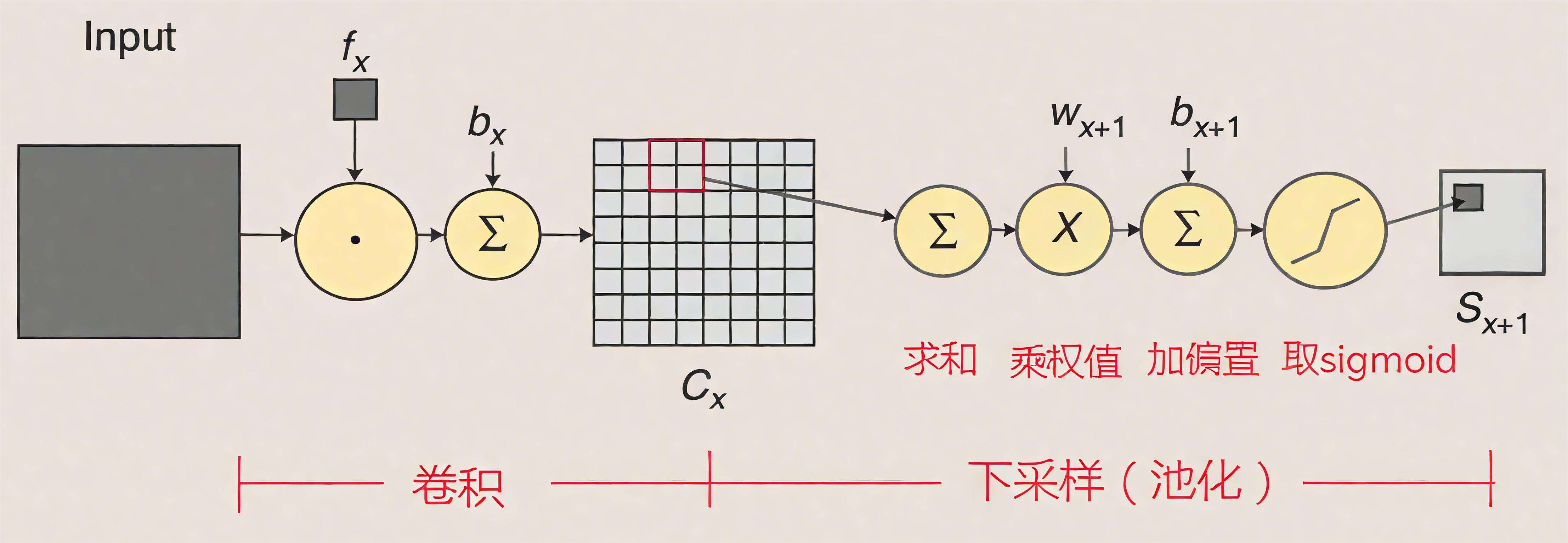
这里有一个非常重要的历史细节和现代实现的区别：

  1. 原始LeNet-5（1998）：如公式所示，虽然池化操作本身（求和）是固定的，但LeCun为每个特征图（feature map）引入了两个可训练的参数（一个缩放系数 w 和一个偏置 b）。所以，严格来说，原始的“子采样层”是一个带有参数的层，但其核心操作仍然是求平均后再缩放。

  2. 现代实现和普遍认知：当我们今天谈论“池化层”时，通常指的是没有任何参数的纯粹池化操作。因此，在绝大多数现代的LeNet-5复现和教程中（例如使用PyTorch/TensorFlow），这一层被简化为了标准的、无参数的平均池化层（AvgPool2d）。可训练的系数和偏置被省略了，因为实践证明它们对于性能的提升并非必要。

所以，当人们现在提到“LeNet-5的池化层”时，默认指的是无参数的平均池化。这也是其与更现代网络（如AlexNet, VGG之后）普遍采用最大池化（Max Pooling） 的一个关键区别。

1.2.3 第三层——卷积层C3

1.2.3.1 具体参数

  • 卷积层C3输入：S2中6个特征图组合

  • 卷积核大小： 5×5

  • 卷积核个数：16

  • 输出featureMap大小：10×10（理由：14-5+1=10）

  • 训练参数：6×(3×5×5+1)+6×(4×5×5+1)+3×(4×5×5+1)+1×(6×5×5+1)=1516

  • 连接数：10×10×1516=151600

1.2.3.2 feature map数量处理

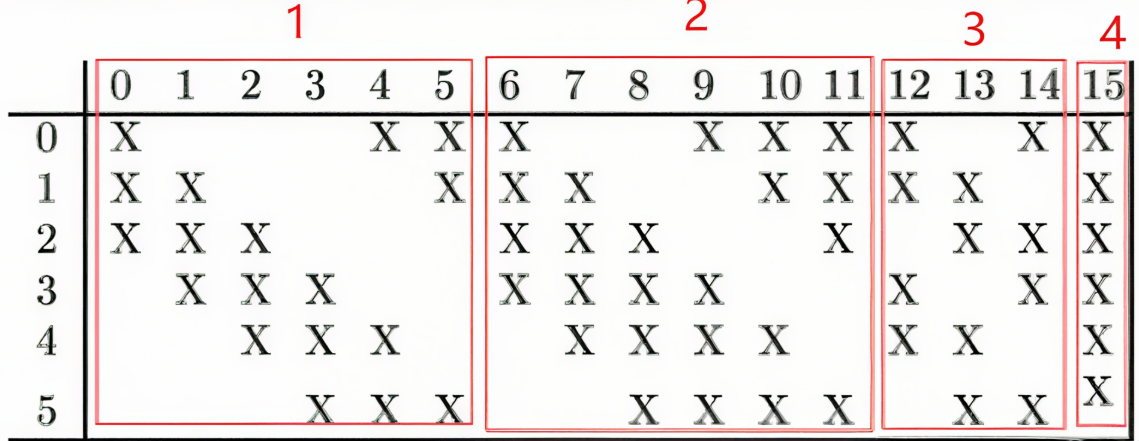
第三层的输入为14×14的6个feature map，卷积核大小为5×5，因此卷积之后输出的feature map大小为10×10。但是由于卷积核有16个，所以希望输出的feature map也为16个，但由于输入只有6个feature map，因此需要进行额外的处理。输入的6个feature map与输出的16个feature map的关系图如下：

  • 红框 1（对应前 6 个输出特征图）：这 6 个输出特征图中的每一个，都与 S2 层中相邻的 3 个输入特征图相连接。也就是说，每个这样的输出特征图是由 S2 层中 3 个相邻的输入特征图通过卷积操作得到的（多通道单卷积核卷积）。

  • 红框 2（对应接下来的 6 个输出特征图）：这 6 个输出特征图中的每一个，都与 S2 层中相邻的 4 个输入特征图相连接。即每个输出特征图由 S2 层中 4 个相邻的输入特征图卷积得到。

  • 红框 3（对应再接下来的 3 个输出特征图）：这 3 个输出特征图中的每一个，都与 S2 层中不相邻的 4 个输入特征图相连接。也就是每个输出特征图由 S2 层中 4 个不相邻的输入特征图卷积得到。

  • 红框 4（对应最后 1 个输出特征图）：这个输出特征图与 S2 层的所有 6 个输入特征图相连接。即该输出特征图是由 S2 层全部 6 个输入特征图卷积得到的。

这种特殊的连接方式，一方面解决了输入输出特征图数量不匹配的问题，另一方面也增加了特征提取的多样性，不同的连接方式可以提取不同的特征模式，使网络能够学习到更丰富的特征表示。

1.2.4 第四层——池化层S4

与S2的操作类似，如果有参数的话（现代网络池化层没有参数）：

  • 输入：上一次C3的输出10×10特征图

  • 池化大小：2×2

  • 池化个数：16

  • 输出featureMap大小：5×5

  • 神经元数量：5×5×16=400

  • 可训练参数：2×16=32

  • 连接数：16×（2×2+1）×5×5=2000

1.2.5 第五层——卷积层C5

  • 输入：S4层的全部16个5×5特征图

  • 卷积核大小：5×5

  • 卷积核种类：120

  • 输出featureMap大小：1×1（通过5-5+1=1得到）

  • 可训练参数/连接：120×（16×5×5+1）=48120

卷积核数目为120个，大小为5×5，由于第四层输出的特征图大小为5×5，因此第五层也可以看成全连接层，输出为120个大小为1×1的特征图。

1.2.6 第六层——全连接层F6

  • 输入：上一层C5输出的120维1×1的向量

  • 输出大小：84

  • 训练参数数目：(120+1)×84=10164

  • 连接数：(120+1)×84=10164

第六层是全连接层。F6层有84个节点，对应于一个7x12的比特图，-1表示白色，1表示黑色，这样每个符号的比特图的黑白色就对应于一个编码。该层的训练参数和连接数是(120 + 1)x84=10164。

1.2.7 输出层

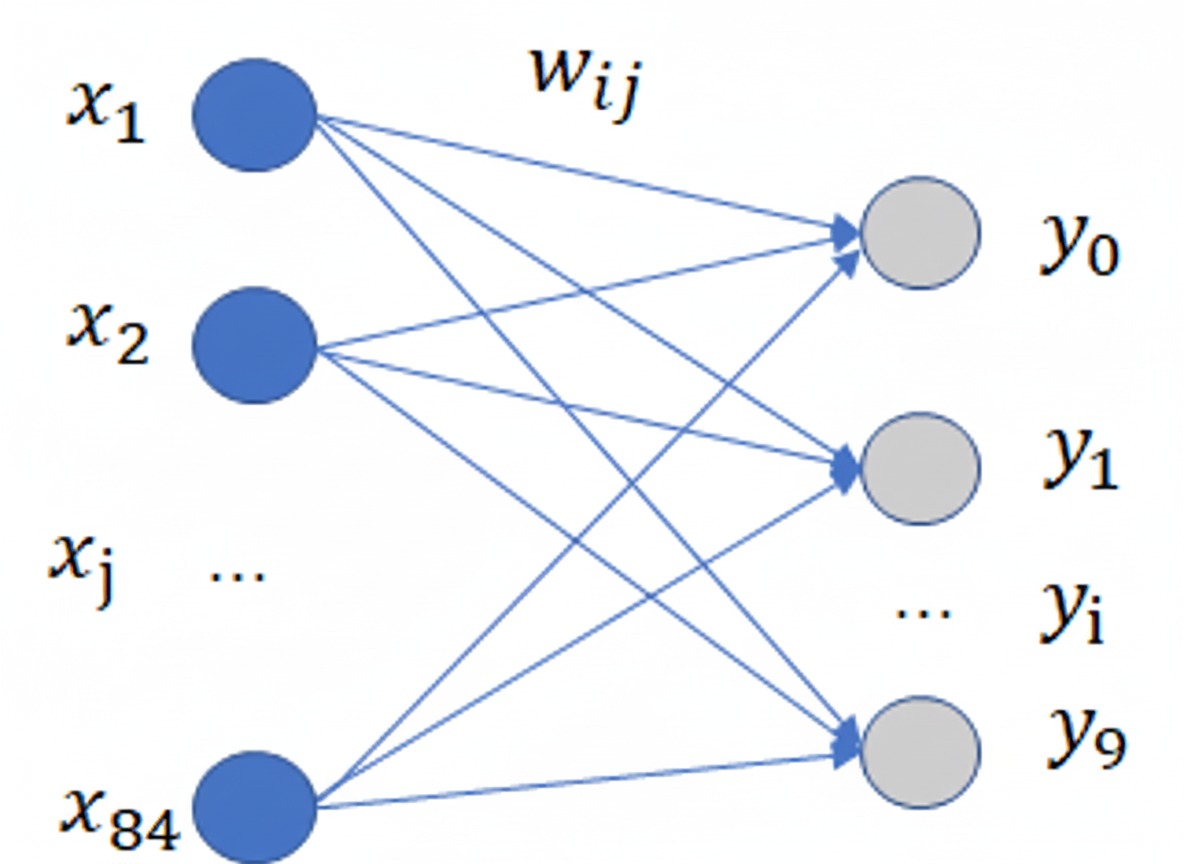
Output层也是全连接层，共有10个节点，分别代表数字0到9。如果第 i 个节点的值为0，则表示网络识别的结果是数字 i 。采用的是径向基函数（RBF）的网络连接方式。假设x是上一层的输入，y是RBF的输出，则RBF输出的计算方式是：

y_i = \sum_j \left( x_j - w_{ij} \right)^2

这公式是什么意思呢？   首先我们应该明白径向基神经网络：它基于距离进行衡量两个数据的相近程度的，RBF网最显著的特点是隐节点采用输人模式与中心向量的距离（如欧氏距离）作为函数的自变量，并使用径向基函数（如高斯函数）作为激活函数。径向基函数关于N维空间的一个中心点具有径向对称性，而且神经元的输人离该中心点越远，神经元的激活程度就越低。上式是基于欧几里得距离，怎么理解那个式子呢？就是说F6层为84个输入用表示 X_i，输出有10个用表示 y_i，而权值 W_{ji} 使用，上式说明所有输入和权值的距离平方和为依据判断，如果越相近距离越小，输出越小则去哪个，如果我们存储的到 W_{ji} 的值为标准的输出。

如标准的手写体0,1,2,3等，那么最后一层就说明。F6层和标准的作比较，和标准的那个图形越相似就说明就越是那个字符的可能性更大。我们看看标准的是什么样的：

上图标准的每个字符都是像素都是12x7=84。这就是解释了为什么F6层的神经元为84个，因为他要把所有像素点和标准的比较在进行判断，因此从这里也可以看出，这里不仅仅可以训练手写体数字，也可以识别其他字符。

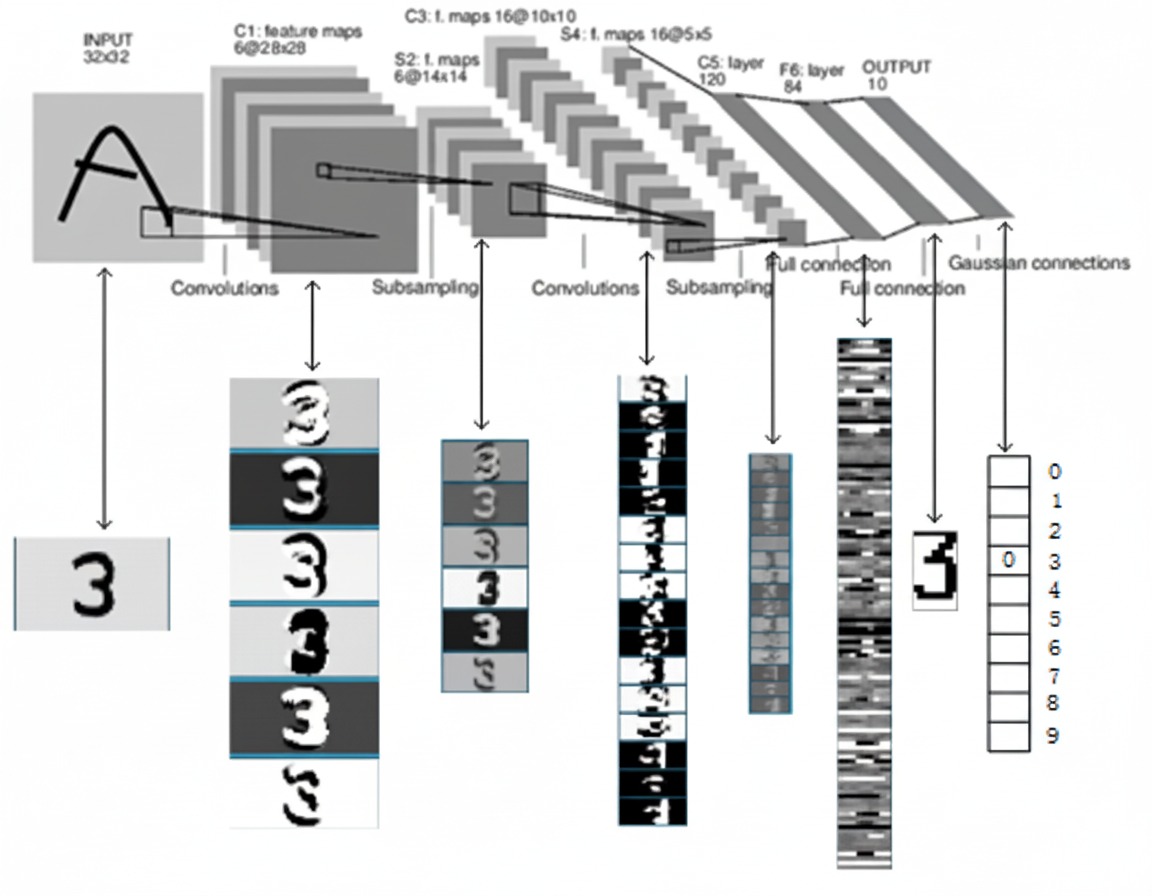
1.3 手写数字识别效果

1.4 基于Pytorch实现

 import torchimport torch.nn as nnimport torch.optim as optimimport torchvision.datasets as datasetsimport torchvision.transforms as transforms​# 定义 LeNet5 模型class LeNet5(nn.Module):def __init__(self):super(LeNet5, self).__init__() # 调用父类构造函数，初始化模型self.conv1 = nn.Conv2d(in_channels=1, out_channels=6, kernel_size=5, stride=1, padding=2)self.pool1 = nn.MaxPool2d(kernel_size=2, stride=2)self.conv2 = nn.Conv2d(in_channels=6, out_channels=16, kernel_size=5, stride=1)self.pool2 = nn.MaxPool2d(kernel_size=2, stride=2)self.fc1 = nn.Linear(16 * 5 * 5, 120)self.fc2 = nn.Linear(120, 84)self.fc3 = nn.Linear(84, 10)#self.relu = nn.ReLU() # 加入该行代码，则可使用下面注释掉的forward()函数# 使用self.relu()比torch.relu()能较为方便替换掉激活函数，符合模块化设计思想，但是一定程度上没那么简洁​'''def forward(self, x):x = self.pool1(self.relu(self.conv1(x)))x = self.pool2(self.relu(self.conv2(x)))x = x.view(-1, 16 * 5 * 5)x = self.relu(self.fc1(x))x = self.relu(self.fc2(x))x = self.fc3(x)return x'''def forward(self, x):x = self.pool1(torch.relu(self.conv1(x)))x = self.pool2(torch.relu(self.conv2(x)))x = x.view(-1, 16 * 5 * 5)x = torch.relu(self.fc1(x))x = torch.relu(self.fc2(x))x = self.fc3(x)return x​# 设置设备device = torch.device("cuda" if torch.cuda.is_available() else "cpu")print(f"Using device: {device}")​# 加载数据集train_dataset = datasets.MNIST(root='./data', train=True, download=False, transform=transforms.ToTensor())test_dataset = datasets.MNIST(root='./data', train=False, download=False, transform=transforms.ToTensor())​# 创建数据加载器train_loader = torch.utils.data.DataLoader(dataset=train_dataset, batch_size=64, shuffle=True)test_loader = torch.utils.data.DataLoader(dataset=test_dataset, batch_size=1000, shuffle=False)​# 创建模型model = LeNet5().to(device)​# 定义损失函数和优化器criterion = nn.CrossEntropyLoss()# optimizer = optim.SGD(model.parameters(), lr=0.01, momentum=0.9)# 用于对比不同优化器效果optimizer = optim.Adam(model.parameters(), lr=0.001)​# 训练模型num_epoch = 10for epoch in range(num_epoch):for i, (images, labels) in enumerate(train_loader):images = images.to(device)labels = labels.to(device)​# 前向传播outputs = model(images)loss = criterion(outputs, labels)​# 反向传播和优化optimizer.zero_grad()loss.backward()optimizer.step()​if (i+1) % 100 == 0:print('Epoch [{}/{}], Step [{}/{}], Loss:{:.4f}'.format(epoch+1, num_epoch, i+1, len(train_loader), loss.item()))​# 测试模型model.eval()with torch.no_grad():correct = 0total = 0for images, labels in test_loader:images = images.to(device)labels = labels.to(device)outputs = model(images)_, predicted = torch.max(outputs.data, 1)total += labels.size(0)correct += (predicted == labels).sum().item()print('Accuracy of the model on the 10000 test images: {} %'.format(100 * correct / total))

数据集文件路径如下：

 LeNet5.pydata/MNIST/raw/t10k-images-idx3-ubytet10k-images-idx3-ubyte.gzt10k-labels-idx1-ubytet10k-labels-idx1-ubyte.gztrain-images-idx3-ubytetrain-images-idx3-ubyte.gztrain-labels-idx1-ubytetrain-labels-idx1-ubyte.gz

实验结果如下：（控制台输出）

  • 使用Adam优化器
Using device: cudaEpoch [1/10], Step [100/938], Loss:0.7215Epoch [1/10], Step [200/938], Loss:0.2004Epoch [1/10], Step [300/938], Loss:0.2631Epoch [1/10], Step [400/938], Loss:0.0894Epoch [1/10], Step [500/938], Loss:0.0816Epoch [1/10], Step [600/938], Loss:0.1352Epoch [1/10], Step [700/938], Loss:0.2386Epoch [1/10], Step [800/938], Loss:0.0636Epoch [1/10], Step [900/938], Loss:0.0689Epoch [2/10], Step [100/938], Loss:0.1709Epoch [2/10], Step [200/938], Loss:0.1755Epoch [2/10], Step [300/938], Loss:0.0378Epoch [2/10], Step [400/938], Loss:0.0452Epoch [2/10], Step [500/938], Loss:0.0927Epoch [2/10], Step [600/938], Loss:0.0380Epoch [2/10], Step [700/938], Loss:0.0885Epoch [2/10], Step [800/938], Loss:0.0450Epoch [2/10], Step [900/938], Loss:0.0289Epoch [3/10], Step [100/938], Loss:0.0381Epoch [3/10], Step [200/938], Loss:0.0689Epoch [3/10], Step [300/938], Loss:0.1033Epoch [3/10], Step [400/938], Loss:0.0055Epoch [3/10], Step [500/938], Loss:0.0280Epoch [3/10], Step [600/938], Loss:0.0553Epoch [3/10], Step [700/938], Loss:0.0227Epoch [3/10], Step [800/938], Loss:0.0183Epoch [3/10], Step [900/938], Loss:0.0874Epoch [4/10], Step [100/938], Loss:0.0410Epoch [4/10], Step [200/938], Loss:0.0085Epoch [4/10], Step [300/938], Loss:0.0602Epoch [4/10], Step [400/938], Loss:0.0108Epoch [4/10], Step [500/938], Loss:0.0131Epoch [4/10], Step [600/938], Loss:0.0361Epoch [4/10], Step [700/938], Loss:0.0114Epoch [4/10], Step [800/938], Loss:0.0466Epoch [4/10], Step [900/938], Loss:0.0128Epoch [5/10], Step [100/938], Loss:0.0999Epoch [5/10], Step [200/938], Loss:0.0022Epoch [5/10], Step [300/938], Loss:0.0107Epoch [5/10], Step [400/938], Loss:0.0239Epoch [5/10], Step [500/938], Loss:0.0820Epoch [5/10], Step [600/938], Loss:0.0458Epoch [5/10], Step [700/938], Loss:0.0360Epoch [5/10], Step [800/938], Loss:0.0145Epoch [5/10], Step [900/938], Loss:0.0144Epoch [6/10], Step [100/938], Loss:0.0149Epoch [6/10], Step [200/938], Loss:0.0134Epoch [6/10], Step [300/938], Loss:0.0348Epoch [6/10], Step [400/938], Loss:0.0018Epoch [6/10], Step [500/938], Loss:0.0080Epoch [6/10], Step [600/938], Loss:0.0103Epoch [6/10], Step [700/938], Loss:0.0064Epoch [6/10], Step [800/938], Loss:0.0185Epoch [6/10], Step [900/938], Loss:0.0449Epoch [7/10], Step [100/938], Loss:0.0161Epoch [7/10], Step [200/938], Loss:0.0071Epoch [7/10], Step [300/938], Loss:0.0664Epoch [7/10], Step [400/938], Loss:0.0597Epoch [7/10], Step [500/938], Loss:0.0204Epoch [7/10], Step [600/938], Loss:0.0175Epoch [7/10], Step [700/938], Loss:0.0161Epoch [7/10], Step [800/938], Loss:0.0047Epoch [7/10], Step [900/938], Loss:0.0831Epoch [8/10], Step [100/938], Loss:0.0038Epoch [8/10], Step [200/938], Loss:0.0351Epoch [8/10], Step [300/938], Loss:0.0229Epoch [8/10], Step [400/938], Loss:0.0046Epoch [8/10], Step [500/938], Loss:0.0161Epoch [8/10], Step [600/938], Loss:0.0248Epoch [8/10], Step [700/938], Loss:0.0056Epoch [8/10], Step [800/938], Loss:0.0582Epoch [8/10], Step [900/938], Loss:0.0431Epoch [9/10], Step [100/938], Loss:0.0009Epoch [9/10], Step [200/938], Loss:0.0054Epoch [9/10], Step [300/938], Loss:0.0335Epoch [9/10], Step [400/938], Loss:0.0088Epoch [9/10], Step [500/938], Loss:0.0156Epoch [9/10], Step [600/938], Loss:0.1397Epoch [9/10], Step [700/938], Loss:0.0523Epoch [9/10], Step [800/938], Loss:0.0007Epoch [9/10], Step [900/938], Loss:0.0112Epoch [10/10], Step [100/938], Loss:0.0007Epoch [10/10], Step [200/938], Loss:0.0011Epoch [10/10], Step [300/938], Loss:0.0064Epoch [10/10], Step [400/938], Loss:0.0024Epoch [10/10], Step [500/938], Loss:0.0171Epoch [10/10], Step [600/938], Loss:0.0567Epoch [10/10], Step [700/938], Loss:0.0253Epoch [10/10], Step [800/938], Loss:0.0284Epoch [10/10], Step [900/938], Loss:0.0082Accuracy of the model on the 10000 test images: 99.01 %​进程已结束，退出代码为 0

  • 使用SGD优化器

Using device: cudaEpoch [1/10], Step [100/938], Loss:1.9961Epoch [1/10], Step [200/938], Loss:0.4239Epoch [1/10], Step [300/938], Loss:0.1415Epoch [1/10], Step [400/938], Loss:0.1971Epoch [1/10], Step [500/938], Loss:0.1232Epoch [1/10], Step [600/938], Loss:0.0781Epoch [1/10], Step [700/938], Loss:0.0322Epoch [1/10], Step [800/938], Loss:0.0653Epoch [1/10], Step [900/938], Loss:0.0665Epoch [2/10], Step [100/938], Loss:0.0958Epoch [2/10], Step [200/938], Loss:0.1979Epoch [2/10], Step [300/938], Loss:0.0830Epoch [2/10], Step [400/938], Loss:0.0905Epoch [2/10], Step [500/938], Loss:0.0977Epoch [2/10], Step [600/938], Loss:0.0771Epoch [2/10], Step [700/938], Loss:0.0285Epoch [2/10], Step [800/938], Loss:0.0982Epoch [2/10], Step [900/938], Loss:0.1310Epoch [3/10], Step [100/938], Loss:0.0540Epoch [3/10], Step [200/938], Loss:0.1522Epoch [3/10], Step [300/938], Loss:0.0652Epoch [3/10], Step [400/938], Loss:0.0906Epoch [3/10], Step [500/938], Loss:0.0087Epoch [3/10], Step [600/938], Loss:0.0087Epoch [3/10], Step [700/938], Loss:0.0351Epoch [3/10], Step [800/938], Loss:0.0458Epoch [3/10], Step [900/938], Loss:0.0982Epoch [4/10], Step [100/938], Loss:0.0765Epoch [4/10], Step [200/938], Loss:0.0297Epoch [4/10], Step [300/938], Loss:0.0237Epoch [4/10], Step [400/938], Loss:0.0228Epoch [4/10], Step [500/938], Loss:0.0205Epoch [4/10], Step [600/938], Loss:0.0019Epoch [4/10], Step [700/938], Loss:0.1155Epoch [4/10], Step [800/938], Loss:0.0245Epoch [4/10], Step [900/938], Loss:0.0067Epoch [5/10], Step [100/938], Loss:0.0152Epoch [5/10], Step [200/938], Loss:0.0108Epoch [5/10], Step [300/938], Loss:0.0053Epoch [5/10], Step [400/938], Loss:0.0378Epoch [5/10], Step [500/938], Loss:0.0411Epoch [5/10], Step [600/938], Loss:0.0080Epoch [5/10], Step [700/938], Loss:0.0455Epoch [5/10], Step [800/938], Loss:0.0068Epoch [5/10], Step [900/938], Loss:0.0066Epoch [6/10], Step [100/938], Loss:0.0075Epoch [6/10], Step [200/938], Loss:0.0028Epoch [6/10], Step [300/938], Loss:0.0301Epoch [6/10], Step [400/938], Loss:0.0012Epoch [6/10], Step [500/938], Loss:0.0836Epoch [6/10], Step [600/938], Loss:0.0029Epoch [6/10], Step [700/938], Loss:0.0146Epoch [6/10], Step [800/938], Loss:0.0705Epoch [6/10], Step [900/938], Loss:0.1705Epoch [7/10], Step [100/938], Loss:0.0552Epoch [7/10], Step [200/938], Loss:0.0051Epoch [7/10], Step [300/938], Loss:0.1357Epoch [7/10], Step [400/938], Loss:0.0515Epoch [7/10], Step [500/938], Loss:0.0190Epoch [7/10], Step [600/938], Loss:0.0782Epoch [7/10], Step [700/938], Loss:0.0443Epoch [7/10], Step [800/938], Loss:0.0033Epoch [7/10], Step [900/938], Loss:0.0046Epoch [8/10], Step [100/938], Loss:0.0350Epoch [8/10], Step [200/938], Loss:0.0022Epoch [8/10], Step [300/938], Loss:0.0024Epoch [8/10], Step [400/938], Loss:0.0461Epoch [8/10], Step [500/938], Loss:0.0116Epoch [8/10], Step [600/938], Loss:0.0007Epoch [8/10], Step [700/938], Loss:0.0019Epoch [8/10], Step [800/938], Loss:0.0253Epoch [8/10], Step [900/938], Loss:0.0415Epoch [9/10], Step [100/938], Loss:0.0021Epoch [9/10], Step [200/938], Loss:0.0147Epoch [9/10], Step [300/938], Loss:0.0223Epoch [9/10], Step [400/938], Loss:0.0556Epoch [9/10], Step [500/938], Loss:0.0210Epoch [9/10], Step [600/938], Loss:0.0008Epoch [9/10], Step [700/938], Loss:0.0075Epoch [9/10], Step [800/938], Loss:0.0025Epoch [9/10], Step [900/938], Loss:0.0022Epoch [10/10], Step [100/938], Loss:0.0036Epoch [10/10], Step [200/938], Loss:0.0119Epoch [10/10], Step [300/938], Loss:0.0052Epoch [10/10], Step [400/938], Loss:0.0016Epoch [10/10], Step [500/938], Loss:0.0003Epoch [10/10], Step [600/938], Loss:0.0035Epoch [10/10], Step [700/938], Loss:0.0010Epoch [10/10], Step [800/938], Loss:0.0003Epoch [10/10], Step [900/938], Loss:0.0194Accuracy of the model on the 10000 test images: 98.99 %​进程已结束，退出代码为 0


文章转载自：

http://okd5bL5k.bsghk.cn
http://PjZp8mCq.bsghk.cn
http://yKYC3564.bsghk.cn
http://kxXC0WkC.bsghk.cn
http://LZotqOJU.bsghk.cn
http://Ps14qTmc.bsghk.cn
http://lypaYioW.bsghk.cn
http://6XnYm8Y1.bsghk.cn
http://tu24gZ1r.bsghk.cn
http://DIK5ZXkn.bsghk.cn
http://B0koNYzh.bsghk.cn
http://IpQl2GKV.bsghk.cn
http://1plDrZQo.bsghk.cn
http://0IEuDBt5.bsghk.cn
http://ojQCJ4xs.bsghk.cn
http://S12mkhqz.bsghk.cn
http://1iyeL4e6.bsghk.cn
http://7wqCNIPG.bsghk.cn
http://1EXH2xfY.bsghk.cn
http://bXeIjs9t.bsghk.cn
http://hMkpHGGK.bsghk.cn
http://UpBJ1piJ.bsghk.cn
http://gSs9oaTU.bsghk.cn
http://x5aH9QI1.bsghk.cn
http://rUuiR5A4.bsghk.cn
http://ugXQUdVQ.bsghk.cn
http://UUkr6UA2.bsghk.cn
http://ULsvjsMO.bsghk.cn
http://pgNeqYba.bsghk.cn
http://x71pHRvm.bsghk.cn
http://www.dtcms.com/a/381083.html

相关文章：

  • 微信小程序开发教程（八）
  • 四川危化品安全员考试题库及答案
  • AI数字人：虚拟世界的新宠儿
  • 数据结构：优先级队列（堆）
  • [Vi] 打开或新建文件
  • Network in Network (NIN)：1×1卷积首次提出
  • 【硬件-笔试面试题-93】硬件/电子工程师，笔试面试题（知识点：波特图）
  • 【RelayMQ】基于 Java 实现轻量级消息队列（九）
  • 机器学习-数据清理、数据变换
  • 测试用例全解析：从入门到精通(1)
  • Linux Netfilter 之 如何完成一个自制的防火墙实例
  • 大语言模型强化学习中的熵崩溃现象：机制、影响与解决方案
  • Netty 源码扩展篇：零拷贝、内存池与背压机制
  • 21.1 《24GB显存搞定LLaMA2-7B指令微调：QLoRA+Flash Attention2.0全流程实战》
  • 前端架构-CSR、SSR 和 SSG
  • range与enumerate的异同与使用
  • Cursor MCP调用流程
  • UBOOT启动流程详解-现代FIT设备加载
  • 中级统计师-统计法规-第七章 统计调查管理
  • 力扣刷题笔记-电话号码的字母组合
  • 基于arduino的视频监控土壤灌溉系统
  • 【硬件-笔试面试题-90】硬件/电子工程师，笔试面试题（知识点：DCDC开关电源的效率计算）
  • 快速理解并记住Python中的可变与不可变对象
  • Netty 调优篇：实战配置、性能监控与常见坑
  • ZYNQ7020+AD9361裸机驱动验证
  • 【超简单】后端入门案例-基于SpringBoot+MyBatis-plus+MySQL图书管理系统
  • 【C++】:list容器全面解析（超详细）
  • Java 笔记 OCA 备考Checked Exception（受检异常）
  • DAY 26 函数专题1：函数定义与参数-2025.9.13
  • MySQL的基础和进阶与运维