数据结构:优先级队列(堆)
1.相关概念
1.1 优先级队列(PriorityQueue)
前面介绍过队列,队列是一种先进先出(FIFO)的数据结构,但有些情况下,操作的数据往往可能带有优先级,一般出队 列时,可能需要优先级高的元素先出队列,该中场景下,使用队列显然不合适。所以在这种情况下,数据结构应该提供两个最基本的操作,一个是返回最高优先级对象,一个是添加新的对象。这种数据结构就是优先级队列(PriorityQueue)。这个单词的发音大家可以自行从翻译软件查看。
1.2 堆的概念及应用
PriorityQueue底层使用了堆这种数据结构,而堆实际就是在完全二叉树的基础上进行了一些调整。
如果有一个关键码的集合K = {k0,k1, k2,…,kn-1},把它的所有元素按完全二叉树的顺序存储方式存储在一个一维数组中,并满足:Ki <= K2i+1 且 Ki<= K2i+2 (Ki >= K2i+1 且 Ki >= K2i+2) i = 0,1,2…,则称为小堆(或大堆)。将根节点最大的堆叫做最大堆或大根堆,根节点最小的堆叫做最小堆或小根堆。
1. 小根堆就是根节点一定比左右孩子节点的值小的完全二叉树,左右孩子节点的值没有要求。
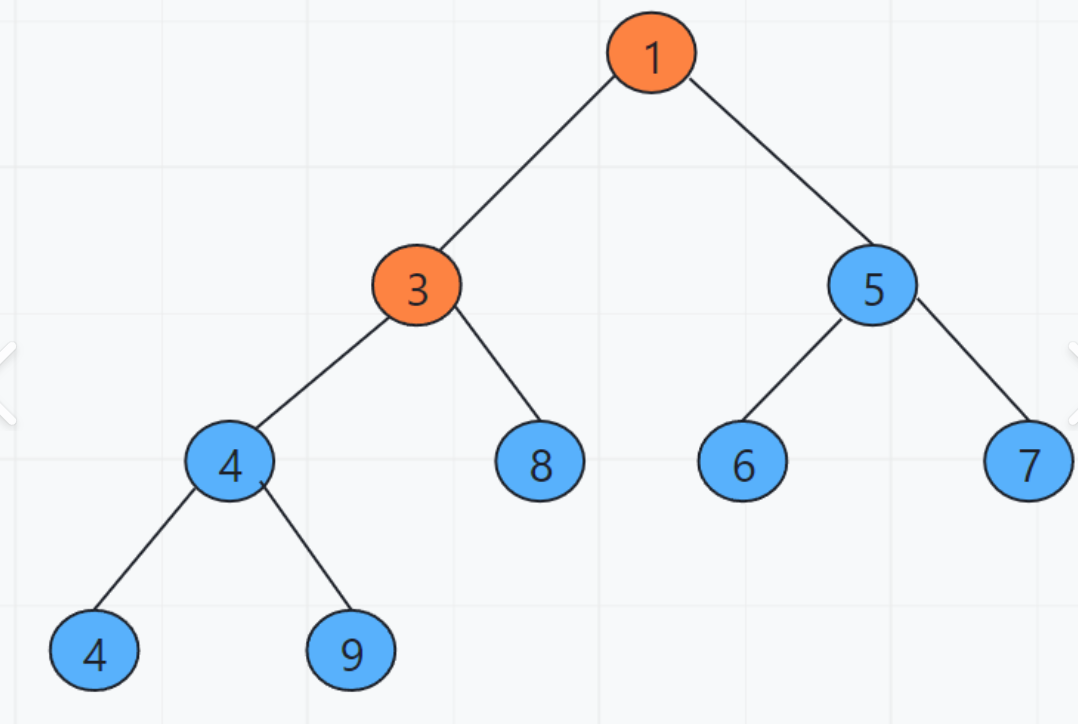
图1:小根堆
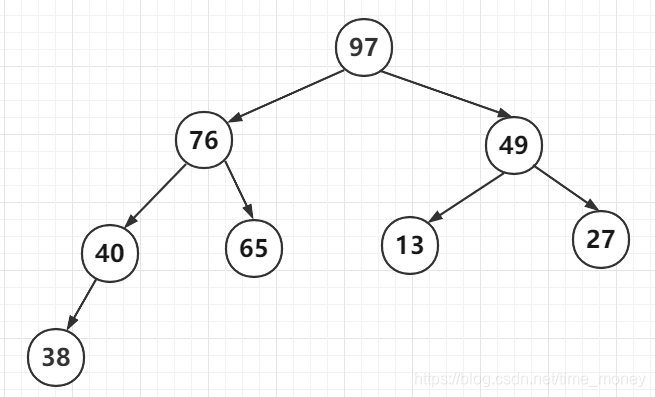
图2:大根堆
堆有以下性质:
1. 堆中某个节点的值总是不大于或不小于其父节点的值;
2. 堆总是一棵完全二叉树。
1.3 堆的存储方式
从堆的概念可知,堆是一棵完全二叉树,因此可以层序的规则采用一维数组的方式来高效存储。那么如果是非完全二叉树呢?还可以用顺序表来存储吗?
注意:对于非完全二叉树,则不适合使用顺序方式进行存储,因为为了能够还原二叉树,数组或空间中必须要存储空节点,就会导致空间利用率比较低。
在我们将元素存储到数组中后,可以根据我上节所讲的二叉树的性质部分对树进行还原。我们假设i为节点在数组中的下标,则有:
1. 如果i为0,则i表示的节点为根节点,否则i节点的双亲节点为 (i - 1)/2;
2. 如果2 * i + 1 小于节点个数,则节点i的左孩子下标为2 * i + 1,否则没有左孩子;
3. 如果2 * i + 2 小于节点个数,则节点i的右孩子下标为2 * i + 2,否则没有右孩子。
这个很重要,在后面关于建立小根堆或大根堆都有相应的作用!
2. 堆的创建和相关操作
堆的创建一般有两种创建方式:向下调整和向上调整。
2.1 调整成小根堆(向下调整)
我们想要把一个堆调整成大根堆或小根堆,一般是采用的向下调整的方式。向上调整也可以的,但是时间复杂度会高。总的来说调整堆也是要遍历整个二叉树的。
思路:
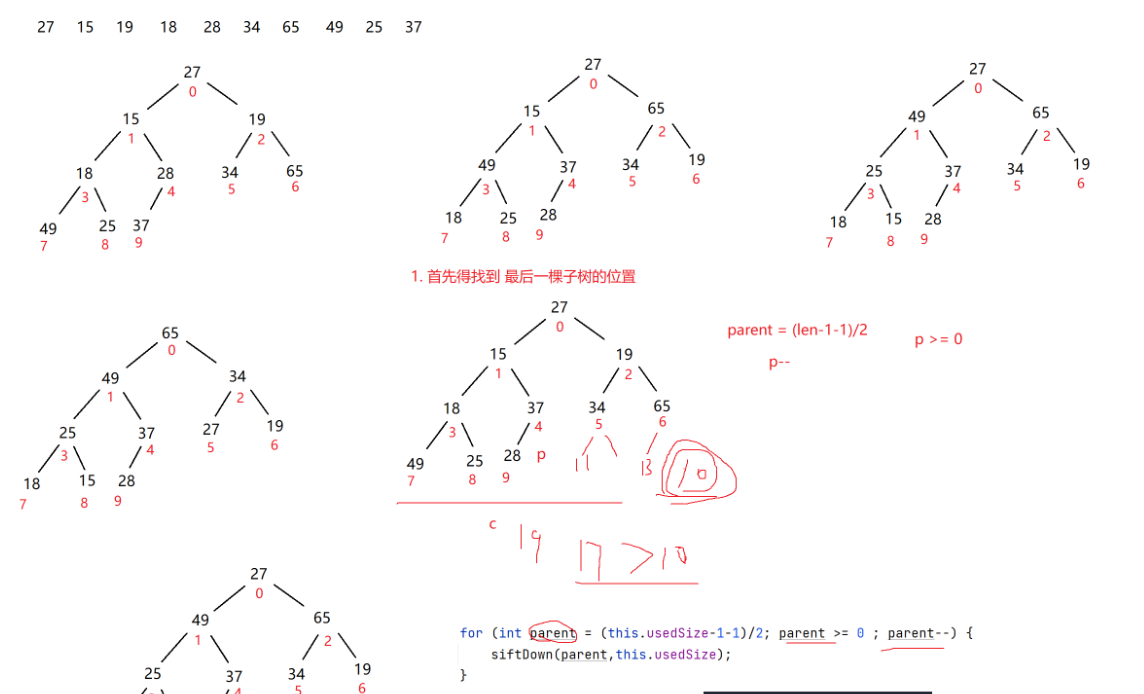
1. 先将该二叉树转化成一个数组。定义出一个usedSize,来代表数组的长度;再定义一个parent和child(parent 代表父节点,child代表子节点(初始是最后一个)),让parent从该数组最后一个元素的父节点,child标记为parent的孩子节点(初始是最后一个);写成循环:每执行一次parent就减减一下,直到parent < 0 就不执行。(本示例写代码时创建树是一个方法,向下调整是一个方法,统计useSize是一个方法,二叉树转化为数组是一个方法)
2. 向下调整时,由于是在不断调换的,所以也要写成一个循环;由于是否要调整的依据是看子节点是否比父节点大,所以循环条件也应该是这个;
现在是调换部分:调换时有可能该父节点有一个子节点或两个子节点,一个子节点时直接交换即可,两个子节点时我们需要先判断这两个子节点哪个子节点更大,然后再以更大的那个来和父节点交换。当然在此之前,我们要判断这个父节点到底是有两个子节点还是一个子节点,相应情况执行相应程序。然后在这之后,一定是要交换了,交换的代码我相信学到这里的大家都会,这里就不赘述了。即当子节点大于父节点时,交换;否则不交换,break跳出循环。
下面是具体代码实现:useSize 和 数组的创建这里不做说明。

2.2 插入、删除操作
关于插入操作,之前在数组中,我们首先要判满,满则扩容;在堆中,因为可以用顺序表堆的方式来实现,故也是要判满,满了我们扩容;然后再来插入操作。注意在最后useSize要 ++;
堆的插入总共需要两个步骤:
1. 先将该元素放入到底层空间中(最后的元素下标 + 1 的地方)(注意:空间不够时需要扩容);
2. 将最后新插入的节点向上调整,直到满足堆的性质。
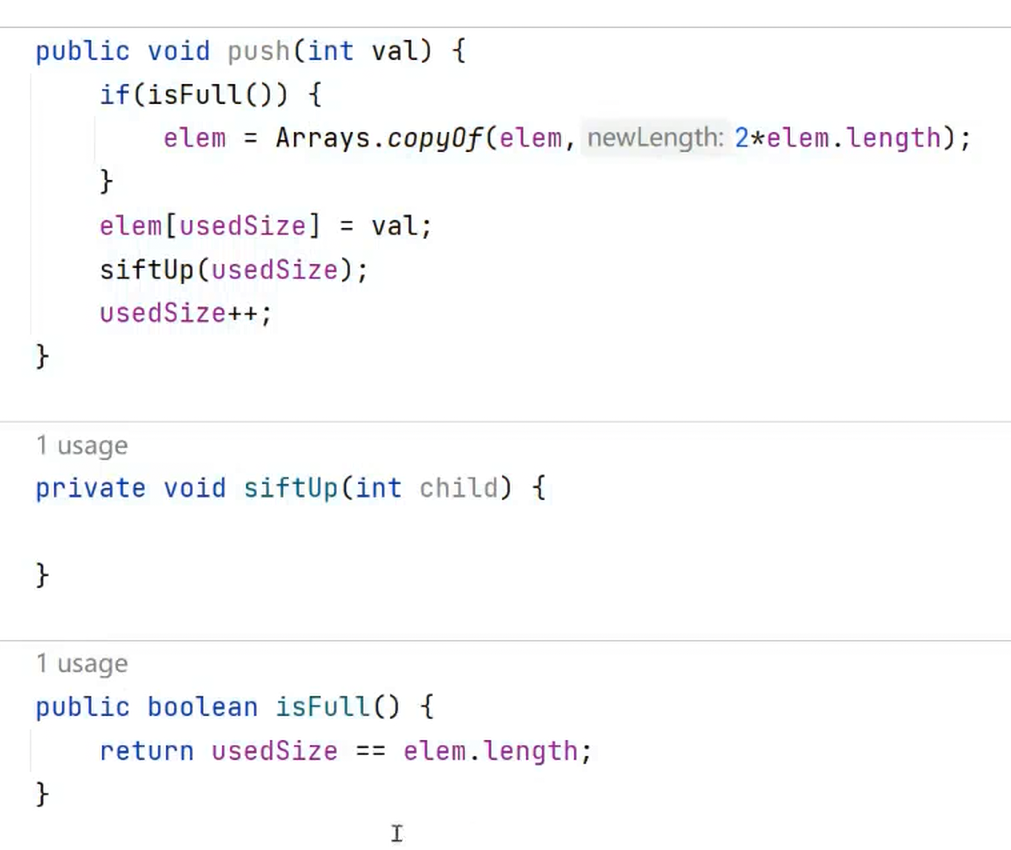
至于插入操作的实现,由于你在插入后有可能原来的小根堆(大根堆)会被破坏,所以在插入之后你还要对堆进行调整。但是注意了,这里使用的是向上调整而不是向下调整。因为插入之前原来就是一个已经被调整好的堆,如图所示:
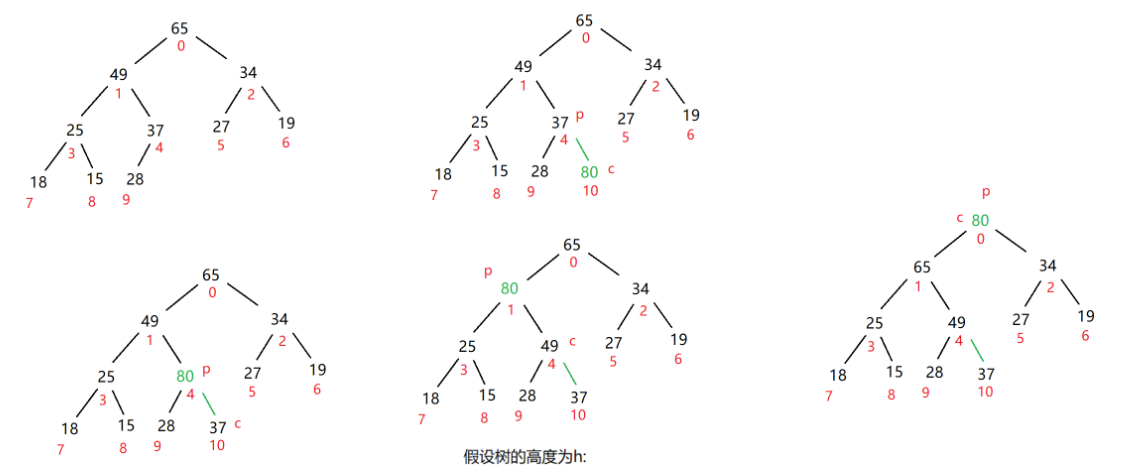
由图可知,在这个堆中所有的节点并没有都被调整过,只有部分进行了调整;如果你这时选择去向下调整,就会多了很多冗余的过程;而向上调整,就能够定位到插入节点的父节点——该父节点的父节点——该父节点的父节点—— ...... —— 根节点的这一条“线”,我们就只需要在这条线上进行调整即可。具体代码实现参考如下:
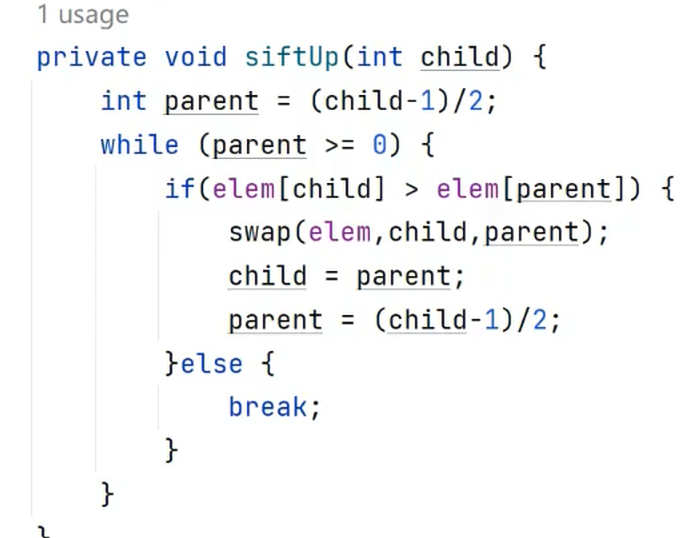
这里的swap(elem,child,parent)其实就是刚才所写的交换的代码,这里是把它改成了方法,这样会看起来更简洁一些。下面的swap同样。
删除操作步骤和思路图具体如下:
1. 将堆顶元素对堆中最后一个元素交换;
2. 将堆中有效数据(useSize)个数减少一个;
3. 对堆顶元素进行向下调整。
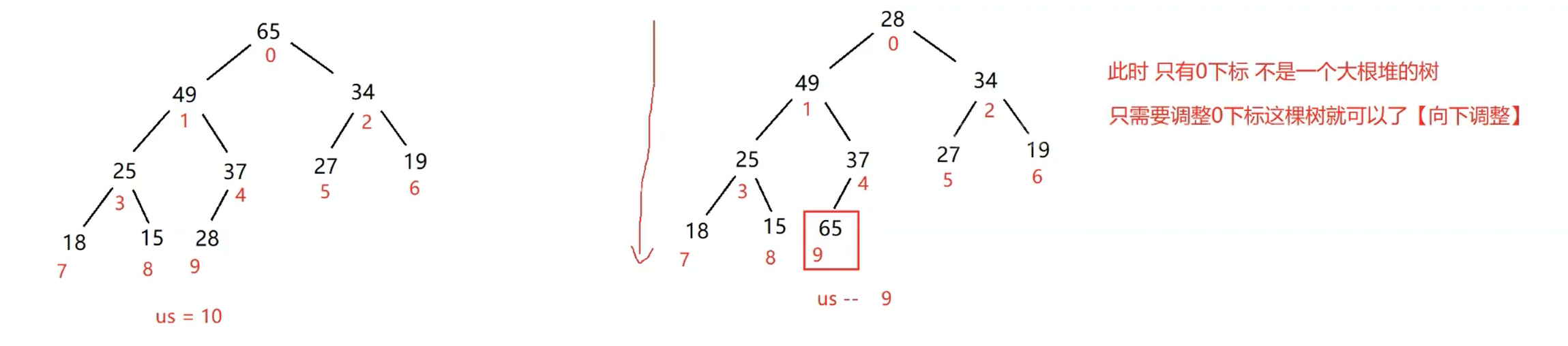
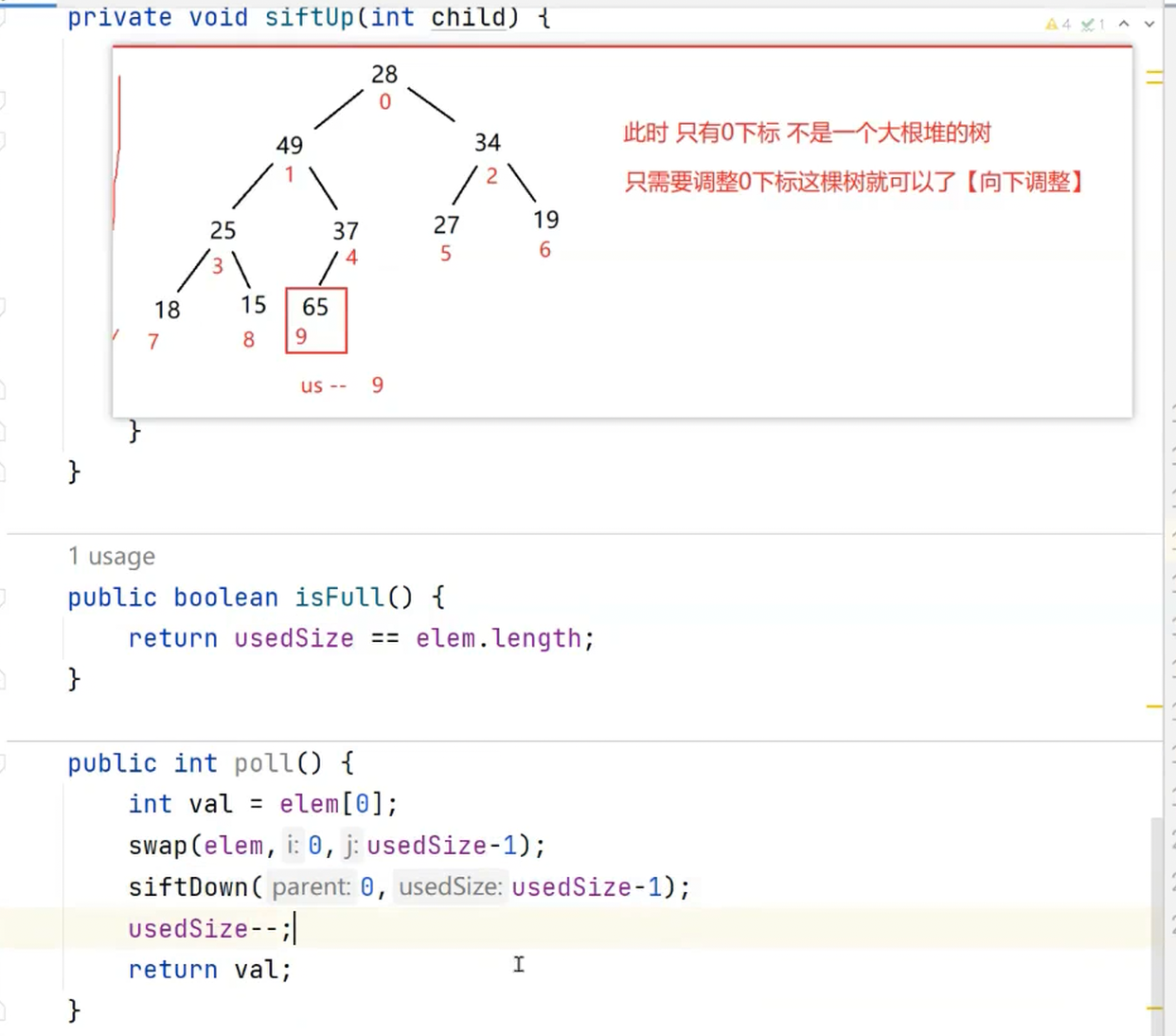
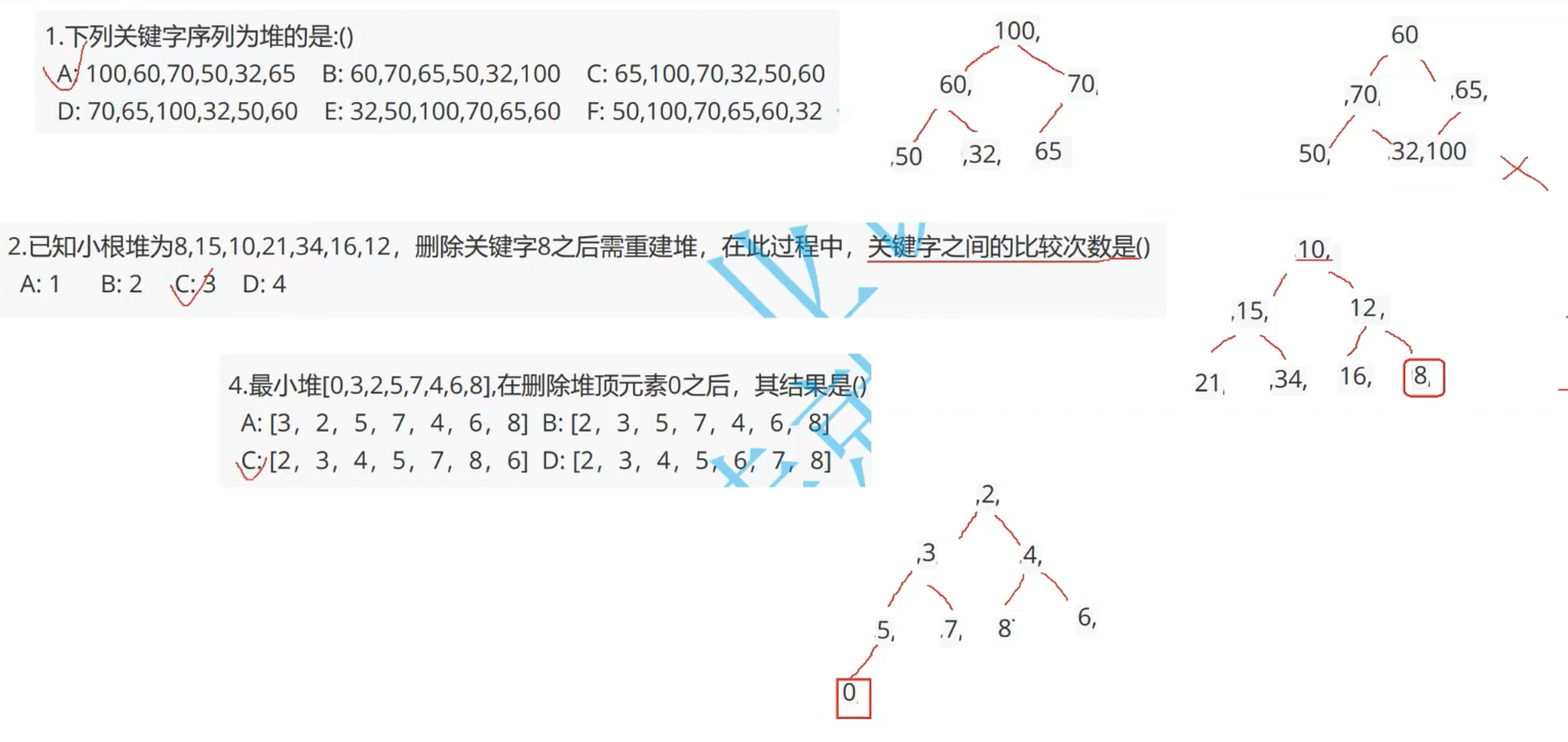
下面先来做几道选择题,巩固一下:

答案:A;堆分为大根堆和小根堆,画图就能知道答案。

答案:C;解析如下。

答案:C;解析如下。
关于PriorityQueue的使用要注意:
1. 使用时必须导入PriorityQueue所在的包;
2. PriorityQueue中放置的元素必须要能够比较大小,不能插入无法比较大小的对象,否则会抛出
ClassCastException异常;
3. 不能插入null对象,否则会抛出NullPointerException;
4. 没有容量限制,可以插入任意多个元素,其内部可以自动扩容;
5. 插入和删除元素的时间复杂度为O(log以2为底的N);
6. PriorityQueue底层使用了堆数据结构;
7. PriorityQueue默认情况下是小根堆---即每次获取到的元素都是最小的元素,如果要改成大根堆则需要创建一个比较器。
下来就是一些PriorityQueue的一些源码与其的功能。看源码可能会有点枯燥乏味,但是还是要看一下,这对于我们的理解也有帮助。
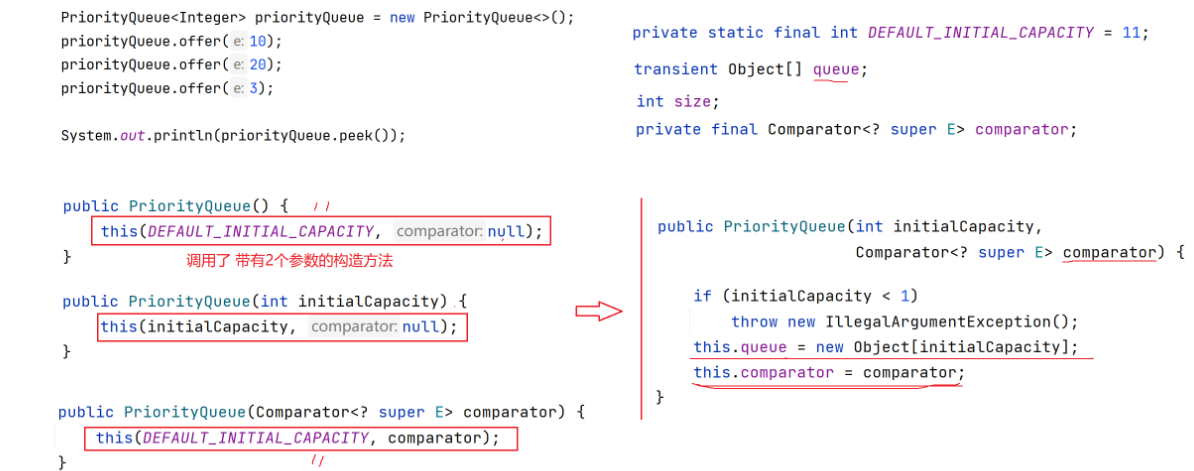
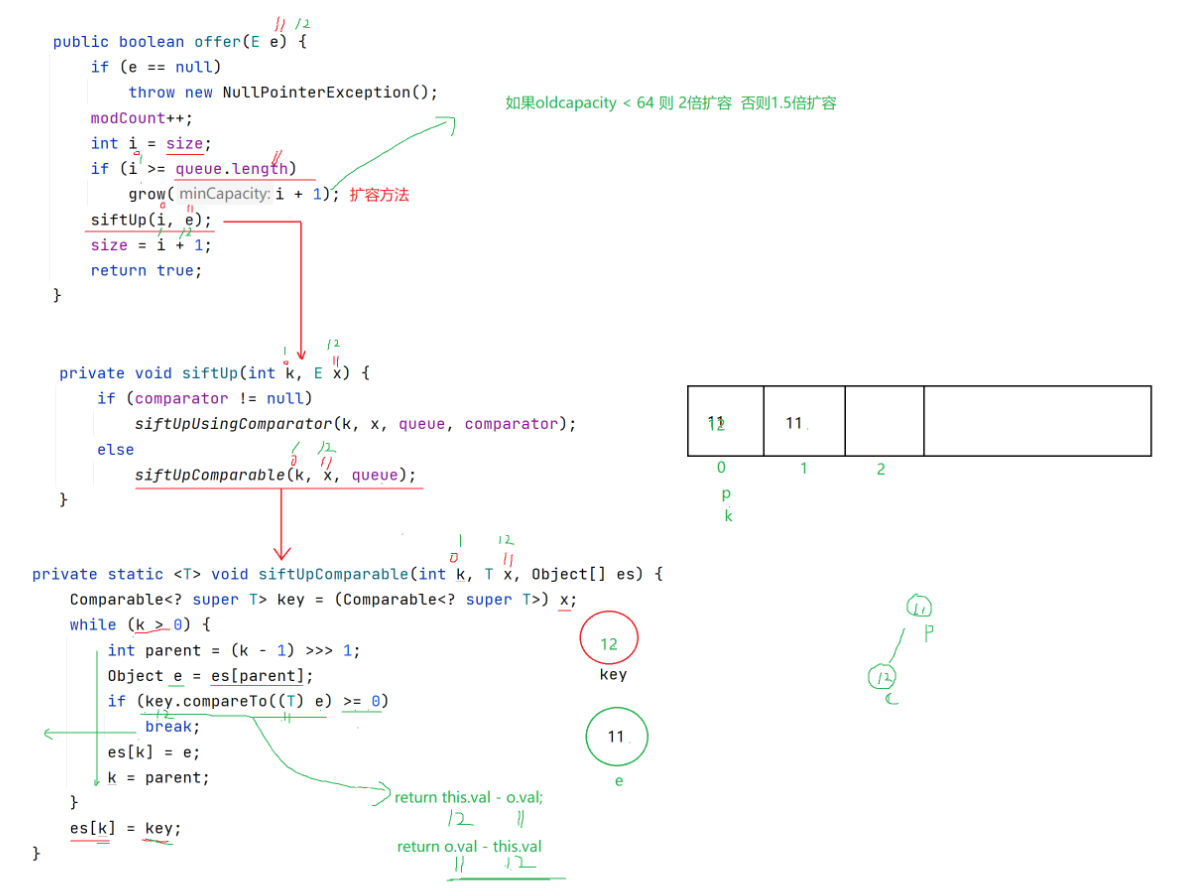

下图是默认小根堆转成大根堆的方法:
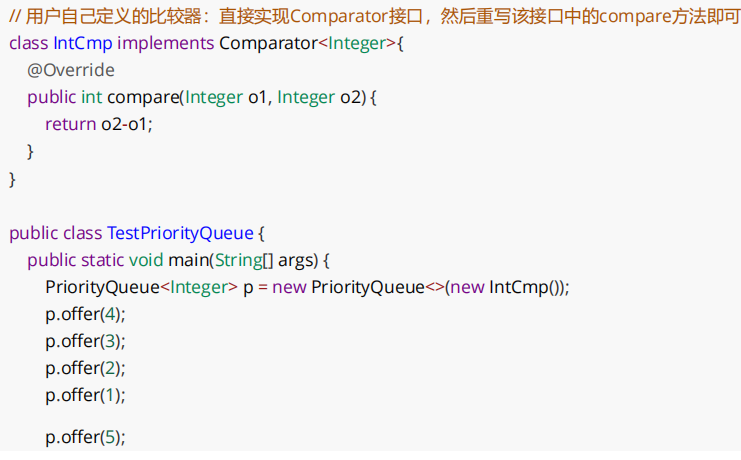
这里顺带再复习一下equals、Comparable、Comparator,它们三者的异同点:

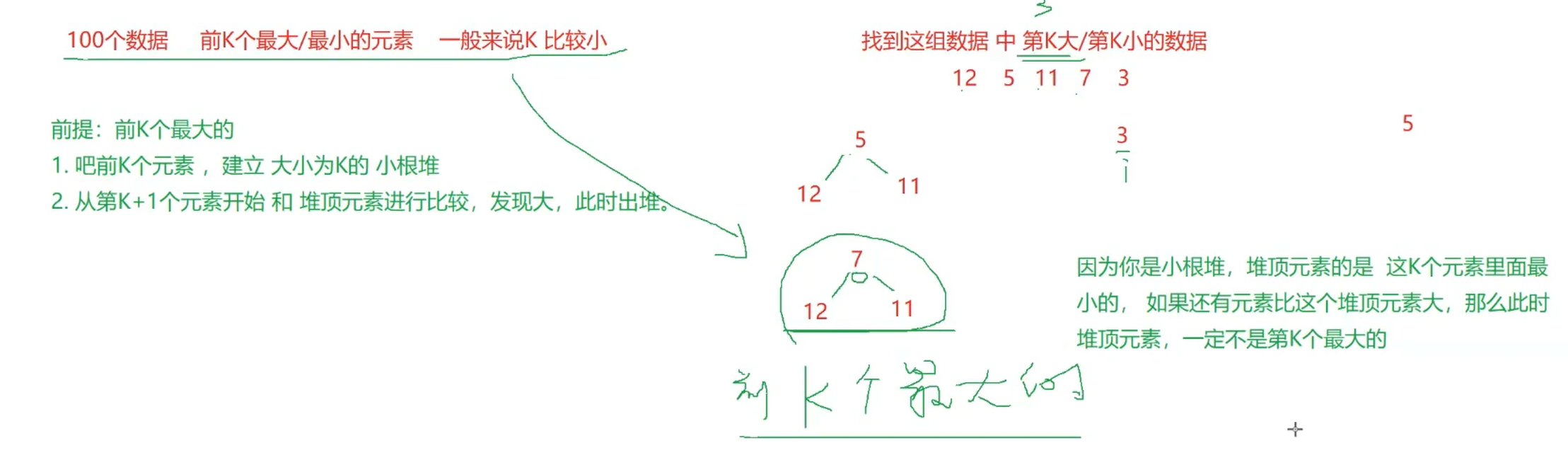
下来又是一个小重点,如何查找堆中前K个最大的元素:
面试题 17.14. 最小K个数 - 力扣(LeetCode)

这里推荐第三种方法,第一种和第二种都是把整个堆重新排列或创建,这样的时间复杂度会相对高;而第三种,只创建了一定数量的堆,最坏的时间复杂度也会比上面那两个好。
那么,本篇文章到此结束!
本篇文章的截图部分摘自于比特科技 。希望能对你有帮助。
