【Luogu】P2613 【模板】有理数取余

题目：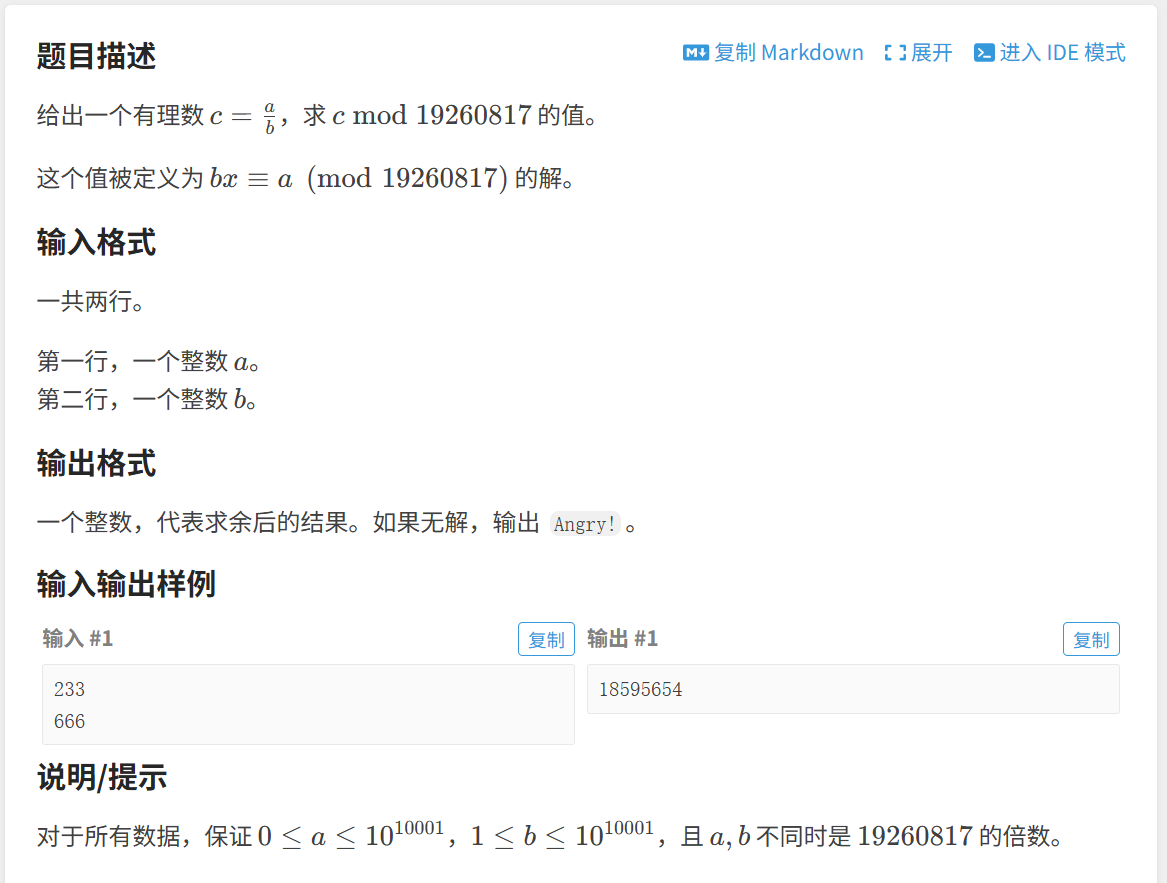

思路：

方法一：

注意到 MOD 是一个质数，所以利用费马小定理和快速幂求 b 的逆元即可

方法二：

利用 exgcd 求得 b 在模 MOD 下的逆元，然后直接 a * inv_b % MOD 即可

特别的：本题数据特别大，但是注意到对 a b 取模不影响结果，所以可以转为字符串进行取模运算

代码：

#include <bits/stdc++.h>
using namespace std;
#define int long long
#define yes cout << "YES\n"
#define no cout << "NO\n"
mt19937 rnd(chrono::steady_clock::now().time_since_epoch().count());
const int MOD = 19260817;
int qp(int a, int b)
{int res = 1;a %= MOD;while (b){if (b & 1)res = res * a % MOD;a = a * a % MOD;b >>= 1;}return res;
}void exgcd(int a,int b,int& x,int& y)
{if(b == 0){x = 1;y = 0;return;}exgcd(b,a%b,x,y);int t = x;x = y;y = t - a/b*y;
}void solve()
{string A, B;cin >> A >> B;int a = 0, b = 0;for (auto &c : A)a = (a * 10 + c - '0') % MOD;for (auto &c : B)b = (b * 10 + c - '0') % MOD;int invb,y;exgcd(b,MOD,invb,y);invb = (invb + MOD) % MOD;cout << a * invb % MOD << endl; //cout << a * qp(b, MOD - 2) % MOD << endl;
}signed main()
{cin.tie(0)->sync_with_stdio(0);int t = 1;while (t--){solve();}return 0;
}