当前位置： 首页 > news >正文

24年秋招-京东-后端开发岗-第1批笔试总结

news 2025/9/13 7:39:07

一

  1. 函数结构：这是一个递归函数，当 n > 0 时，会递归调用自身 2 次（foo(n-1, x+1, y) 和 foo(n-1, x, y+1)），当 n ≤ 0 时触发终止条件（仅执行简单的加法操作，时间复杂度为 O (1)）。

  2. 递归调用次数：

    • 设 T(n) 为函数处理输入 n 时的时间复杂度。
    • 递归关系为：T(n) = 2 × T(n-1)（每次调用产生 2 个规模为 n-1 的子问题）。
    • 终止条件：T(0) = O(1)（无需递归，直接计算）。

  3. 展开计算：

    • T(n) = 2 × T(n-1)
    • T(n) = 2 × 2 × T(n-2) = 2² × T(n-2)
    • ...
    • 最终展开为：T(n) = 2ⁿ × T(0) = O(2ⁿ)

因此，该函数的时间复杂度为 指数级 O (2ⁿ)，随着 n 的增大，执行时间会急剧增长。

二

“缺页”（Page Fault），简单来说：当程序试图访问某个 “虚拟内存页面” 时，发现该页面并未加载到计算机的 “物理内存” 中，此时就会触发 “缺页” 事件。

要计算 LRU（最近最少使用）算法的缺页数，我们需要模拟页面访问过程，跟踪主存块的使用情况：

  • 初始状态：3 个主存块均为空（缺页时会分配新块）
  • 访问序列：{1, 3, 2, 1, 2, 1, 5, 1, 2, 3}
  • LRU 规则：当主存块满时，替换最久未被访问的页面

模拟过程：

步骤访问页面主存块状态（最近使用的页面在右侧）是否缺页
11[1]缺页（1）
23[1, 3]缺页（2）
32[1, 3, 2]缺页（3）
41[3, 2, 1] （1 被访问，移至最近位置）不缺页
52[3, 1, 2] （2 被访问，移至最近位置）不缺页
61[3, 2, 1] （1 被访问，移至最近位置）不缺页
75[2, 1, 5] （替换最久未用的 3）缺页（4）
81[2, 5, 1] （1 被访问，移至最近位置）不缺页
92[5, 1, 2] （2 被访问，移至最近位置）不缺页
103[1, 2, 3] （替换最久未用的 5）缺页（5）

结果：

采用 LRU 算法时，总缺页数是 5 次。

本题主要考察的是传输层中两个非常重要的协议之间的区别。

在网络操作系统中，TCP和UDP是传输层中两个非常重要的协议。

TCP提供的是面向连接的、可靠的端到端通信机制，因此TCP协议在注重数据安全的场景下获得了极为广泛的应用，A选项是正确的。

TCP采用了确认和重发机制来确保数据的可靠传输，B选项正确。

相较于UDP，TCP的优势在于保证了传输的安全性与可靠性，所以D选项是正确的，但传输效率方面TCP不及UDP，C选项错误。

知识点：网络基础、测试、后端开发、客户端开发、前端开发、数据、运维/技术支持

三

答案：A

A，SSL(Secure Sockets Layer 安全套接层)，是https采用的加密通道

B，IPSec（InternetProtocolSecurity）用以提供公用和专用网络的端对端加密和验证服务。

C，PGP(Pretty Good Privacy)，是一个基于RSA公钥加密体系的邮件加密系统

D，SET是安全电子交易协议，是为了在互联网上进行在线交易时保证信用卡支付的安全而设立的一个开放的规范

知识点：2015、网络基础、Java工程师、C++工程师、计算机网络、测试、后端开发、客户端开发、前端开发、数据、运维/技术支持

四

B选项，MyISAM支持全文索引，用于查找文本中的关键词，而InnoDB在MySQL5.6版本后也支持全文索引。

C选项，InnoDB支持事务，对于每一条SQL语言都默认封装成事务，而MyISAM不支持事务。

D选项，InnoDB支持外键，而MyISAM不支持外键，因此含有外键的InnoDB表不能转换为MYISAM表。

知识点：数据库、测试、后端开发、客户端开发、前端开发、人工智能/算法、数据、运维/技术支持

五

SQL Server中每一条select、insert、update、delete语句都是隐形事务的一部分，显性事务用BEGIN TRANSACTION明确指定事务。

知识点：数据库、SQL、SQL+MySQL

六

sed 命令是利用脚本来处理文本文件，sed 可依照脚本的指令来处理、编辑文本文件，主要用来自动编辑一个或多个文件、简化对文件的反复操作、编写转换程序等。

s 表示替换命令，/AAA 表示匹配 "AAA"，/BBB 表示把匹配替换成 "BBB"，/g 表示全局匹配。

> xyz 表示将内容重定向到 xyz 文件中。

知识点：Linux

七

八

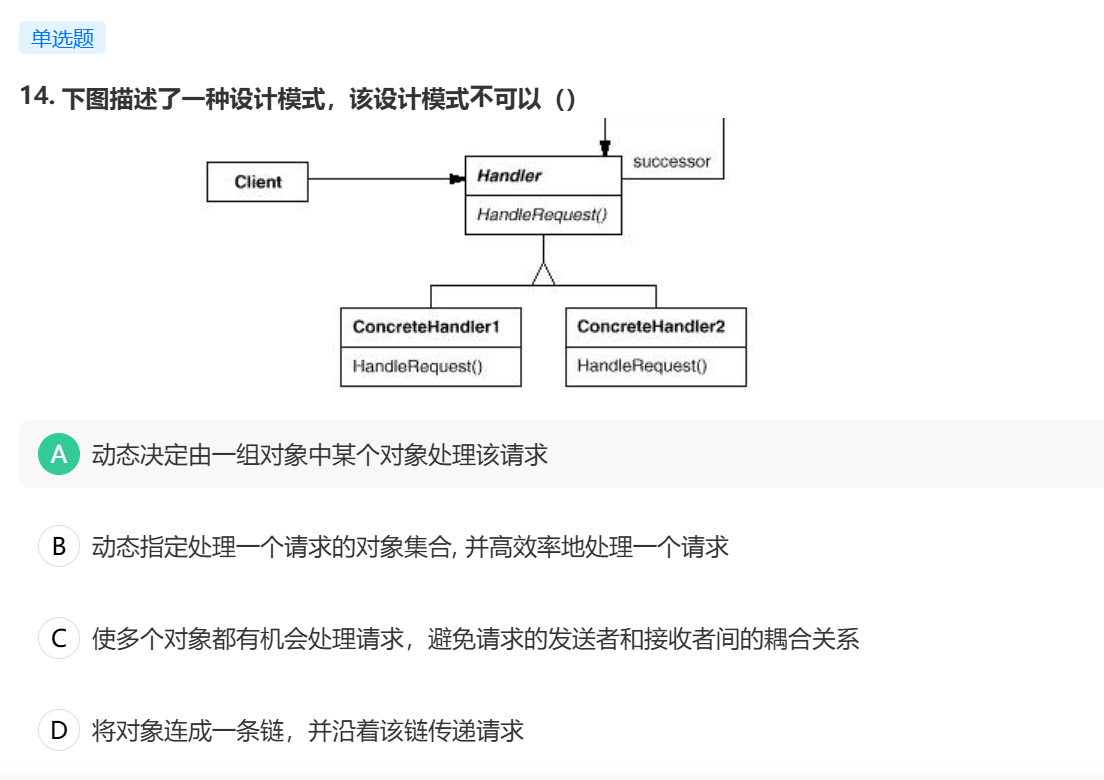
责任链模式使一种对象行为模式，它将多个对象连成一条链，并沿着该链传递请求，链路上的每一个对象都有机会处理这个请求，它提供了一种松耦合的机制。

知识点：设计模式

九

import java.util.Scanner;// 注意类名必须为 Main, 不要有任何 package xxx 信息
public class Main {public static void main(String[] args) {Scanner in = new Scanner(System.in);// 注意 hasNext 和 hasNextLine 的区别int length = in.nextInt();long[] a = new long[length];for (int i = 0; i < length; i++) {a[i] = in.nextInt();}System.out.println(minPay(a));}public static long minPay(long[] num) {long sum = 0;for (long n : num) {sum += n;}long min = Long.MAX_VALUE;;long leftSum = 0;for (int i = 0 ; i < num.length - 1; i++) {leftSum += num[i];if (leftSum * (sum - leftSum) < min) min = leftSum * (sum - leftSum);}return min;}
}

十

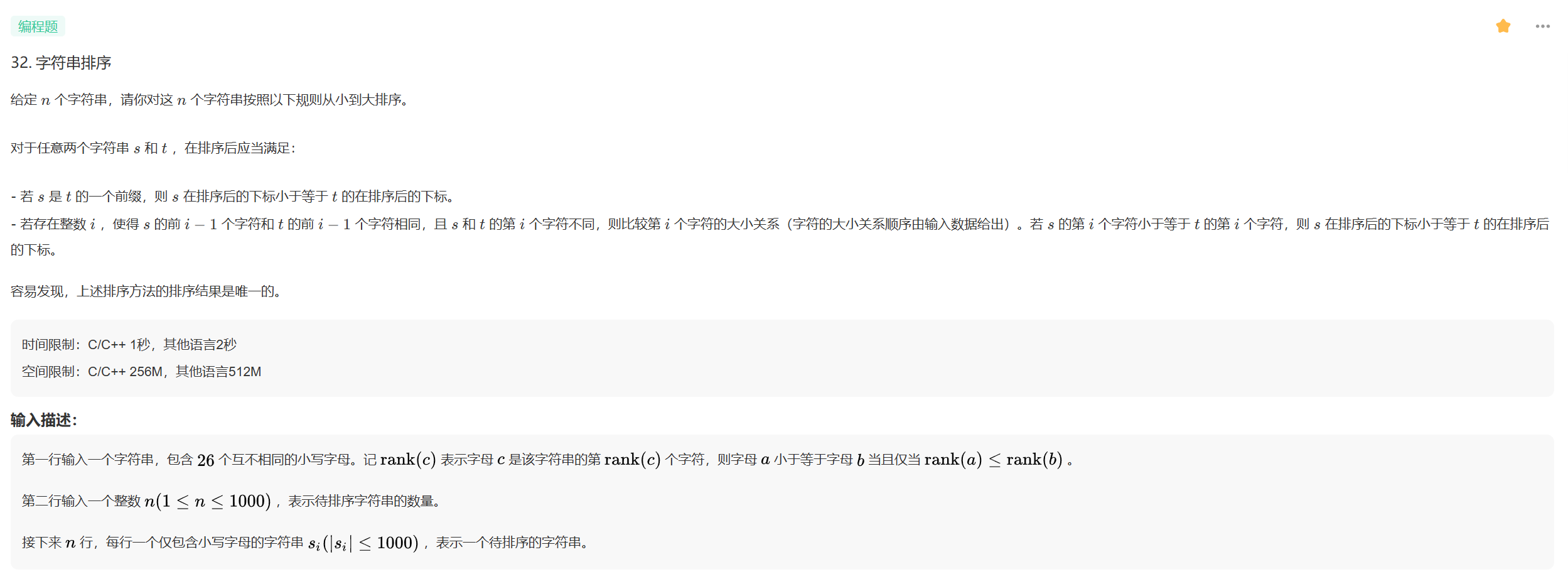
思路：通过自定义比较器来进行排序。

相关知识点注意事项：Java自定义比较器详解-CSDN博客https://blog.csdn.net/weixin_73847538/article/details/151620549?sharetype=blogdetail&sharerId=151620549&sharerefer=PC&sharesource=weixin_73847538&spm=1011.2480.3001.8118
java.util.Scanner及其注意事项-CSDN博客https://blog.csdn.net/weixin_73847538/article/details/151620387?spm=1011.2124.3001.6209

import java.util.*;  // 注意类名必须为 Main, 不要有任何 package xxx 信息
public class Main {public static void main(String[] args) {Scanner in = new Scanner(System.in);         // 注意 hasNext 和 hasNextLine 的区别String sortStr = in.nextLine();int count = in.nextInt();in.nextLine();List<String> strings = new ArrayList<>();for (int i = 0; i < count; i++) {strings.add(in.nextLine());}sortByStr(sortStr, strings);}public static void sortByStr(String s, List<String> str) {char[] c = s.toCharArray();Map<Character, Integer> map = new HashMap<>();for (int i = 0; i < c.length; i++) {map.put(c[i], i);}Collections.sort(str, new Comparator<String>() {@Overridepublic int compare(String s1, String s2) {if(s1.equals(s2)) return 0;if (s1.startsWith(s2, 0)) return 1;if (s2.startsWith(s1, 0)) return -1;for (int i = 0; i < Integer.min(s1.length(), s2.length()); i++) {if (s1.charAt(i) == s2.charAt(i)) continue;return Integer.compare(map.get(s1.charAt(i)),map.get(s2.charAt(i)));}return Integer.compare(s1.length(), s2.length());}});for (String x : str) {System.out.println(x);}}
}

十一

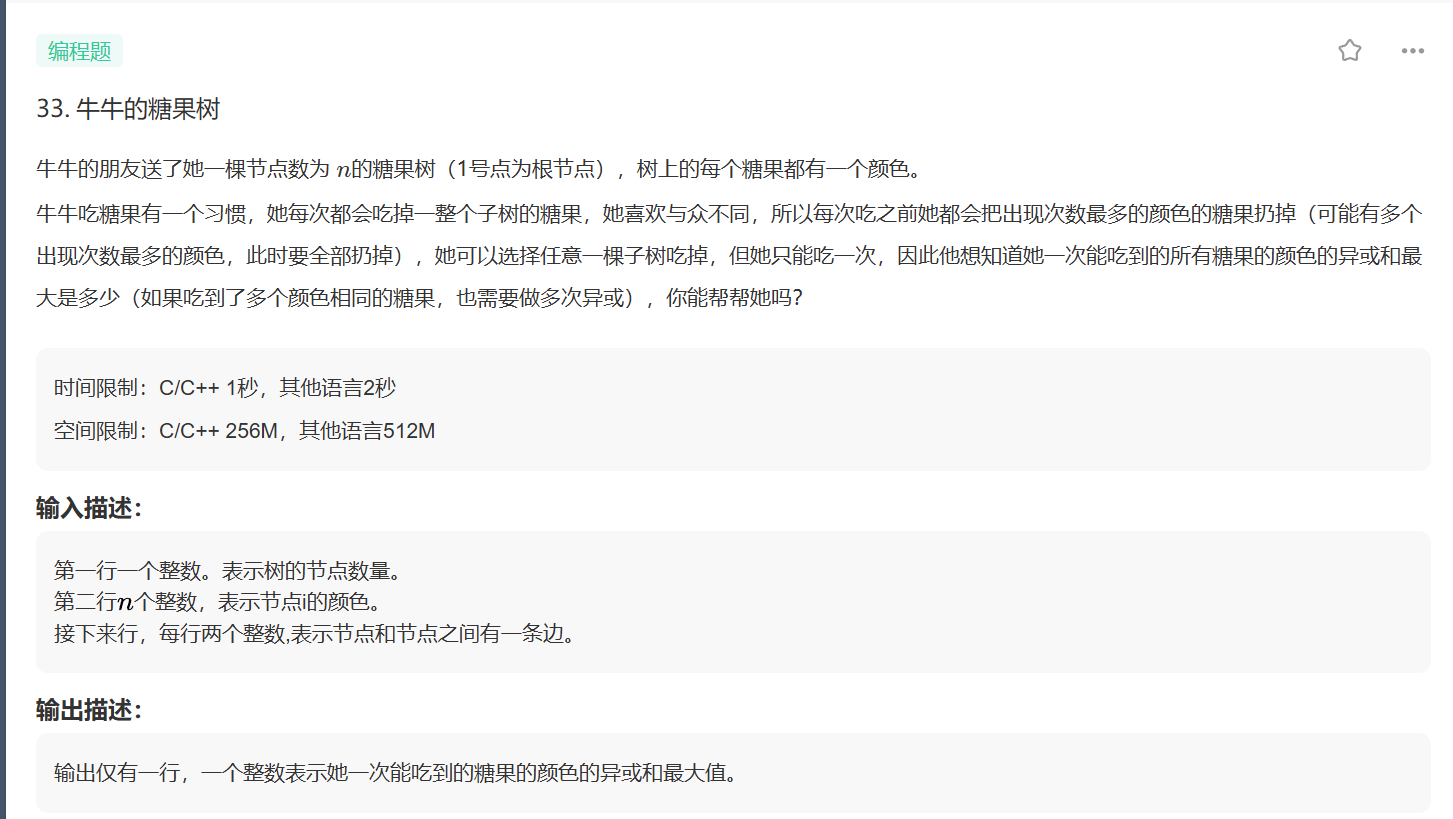
思路：

  1. 树的构建与预处理：用邻接表存储树的边，通过 DFS/BFS 从根节点（1 号）出发，构建 “子节点列表”，明确每个节点的后代，同时用数组存储各节点颜色。

  2. 子树信息统计：用后序 DFS 遍历所有节点（每个节点作为子树根），合并其所有子节点的颜色频次（各颜色出现次数）和总异或和（子树所有颜色异或结果），再加入自身颜色信息，一次遍历完成所有子树的信息统计，避免重复计算。

  3. 计算子树处理后异或和：对每个子树，先找颜色最大出现次数，再计算所有该频次颜色的异或贡献（奇数次为颜色本身，偶数次为 0），用子树总异或和异或该贡献，得到处理后异或和（即扔掉最多频颜色后的结果）。

  4. 求最大值：遍历所有子树的处理后异或和，记录最大值即为答案

import java.util.*;public class Main {static List<List<Integer>> children; // 子节点列表static int[] color; // 节点颜色（1-based）static int maxXor = 0; // 最终答案public static void main(String[] args) {Scanner sc = new Scanner(System.in);int n = sc.nextInt();color = new int[n + 1];for (int i = 1; i <= n; i++) {color[i] = sc.nextInt();}// 构建邻接表List<List<Integer>> adj = new ArrayList<>();for (int i = 0; i <= n; i++) {adj.add(new ArrayList<>());}for (int i = 0; i < n - 1; i++) {int u = sc.nextInt();int v = sc.nextInt();adj.get(u).add(v);adj.get(v).add(u);}// 构建子节点列表（从根1出发，BFS/DFS）children = new ArrayList<>();for (int i = 0; i <= n; i++) {children.add(new ArrayList<>());}boolean[] visited = new boolean[n + 1];buildTree(1, visited, adj); // 1是根节点// 后序DFS统计所有子树信息，并计算异或和dfs(1);System.out.println(maxXor);}// 构建子节点列表（DFS）static void buildTree(int u, boolean[] visited, List<List<Integer>> adj) {visited[u] = true;for (int v : adj.get(u)) {if (!visited[v]) {children.get(u).add(v);buildTree(v, visited, adj);}}}// 后序DFS：返回当前子树的[颜色频次数组, 总异或和]static Object[] dfs(int u) {int[] cnt = new int[1001]; // 颜色频次（颜色<=1000）int totalXor = 0;// 1. 合并所有子节点的信息for (int v : children.get(u)) {Object[] childRes = dfs(v);int[] childCnt = (int[]) childRes[0];int childXor = (int) childRes[1];// 合并频次for (int c = 1; c <= 1000; c++) {cnt[c] += childCnt[c];}// 合并总异或和totalXor ^= childXor;}// 2. 加入当前节点u的信息int c = color[u];cnt[c]++;totalXor ^= c;// 3. 计算当前子树的处理后异或和// 找max_cntint maxCnt = 0;for (int i = 1; i <= 1000; i++) {if (cnt[i] > maxCnt) {maxCnt = cnt[i];}}// 计算del_xorint delXor = 0;for (int i = 1; i <= 1000; i++) {if (cnt[i] == maxCnt) {// 贡献：奇数次为i，偶数次为0if (cnt[i] % 2 == 1) {delXor ^= i;}}}// 处理后异或和int currentXor = totalXor ^ delXor;// 更新最大值if (currentXor > maxXor) {maxXor = currentXor;}// 4. 返回当前子树的信息给父节点return new Object[] {cnt, totalXor};}
}


文章转载自：

http://2zdyBynf.tqygx.cn
http://hyCJ3kQd.tqygx.cn
http://52Attqmt.tqygx.cn
http://9cmpxSAS.tqygx.cn
http://EKBU22b1.tqygx.cn
http://FamiHwKm.tqygx.cn
http://twOL9RgG.tqygx.cn
http://1COhY6iS.tqygx.cn
http://i05Ut73x.tqygx.cn
http://gj1tENuw.tqygx.cn
http://pj5dZ013.tqygx.cn
http://E5nI0WzV.tqygx.cn
http://HOrsv0Hq.tqygx.cn
http://51f3tPdS.tqygx.cn
http://cGvKeRiO.tqygx.cn
http://vC24yEx1.tqygx.cn
http://0wKcFMjn.tqygx.cn
http://xIesLNAY.tqygx.cn
http://CwB9BTIj.tqygx.cn
http://1aYUWLcn.tqygx.cn
http://gHuBjhge.tqygx.cn
http://0PN38ak0.tqygx.cn
http://3mA1QBkT.tqygx.cn
http://X0UhQb9F.tqygx.cn
http://IQD9dhBz.tqygx.cn
http://X61TmPtc.tqygx.cn
http://jRTpbAyz.tqygx.cn
http://91xXZBa2.tqygx.cn
http://3WeyzOXW.tqygx.cn
http://56XclmOi.tqygx.cn
http://www.dtcms.com/a/380372.html

相关文章：

  • 技术与情感交织的一生 （十三）
  • 1 环境配置
  • 老年人生活照护实训室：支撑照护实操教学的关键场所
  • 俄罗斯方块终端游戏实现 —— C语言系统编程与终端控制
  • 跨屏互联KuapingCMS建站系统发布更新 增加seo自动外链功能
  • 域账号提权后权限管理问题解析
  • Go语言设计模式(七)组合模式
  • 解密完全二叉树顺序存储之堆结构
  • 【Vue2 ✨】Vue2 入门之旅 · 进阶篇（三）：模板编译原理
  • 嵌入式仿真技术在教学中的应用与挑战探析
  • Kaggle项目实践——Titanic: Machine Learning from Disaster
  • 【leetcode】127. 三角形的最小路径和
  • Java设计模式中的几种常用设计模式
  • 【Vue2 ✨】Vue2 入门之旅 · 进阶篇（四）：异步更新与 nextTick 原理
  • 【小程序】微信小程序九宫格抽奖动画（完整版）
  • [BJDCTF 2020]encode
  • 系统核心解析：深入操作系统内部机制——进程管理与控制指南（一）【进程/PCB】
  • 速通ACM省铜第二天 赋源码（Adjacent XOR和Arboris Contractio）
  • Python快速入门专业版（二十四）：while循环：条件循环与“死循环”避免（猜数字游戏案例）
  • 神经网络构成框架-理论学习
  • 智能眼镜产品成熟度分析框架与评估
  • 从零学算法2327
  • 【C++】:list容器全面解析
  • 渲染农场多少钱一小时
  • IDEA试用过期，无法登录，重置方法
  • IP验证学习之case编写
  • 通过Dockerfile构建Docker镜像并训练模型
  • 操作系统内核架构深度解析：从微内核到宏内核的设计哲学与性能权衡
  • IIS运行账户设置记录
  • 服务管理 systemctl