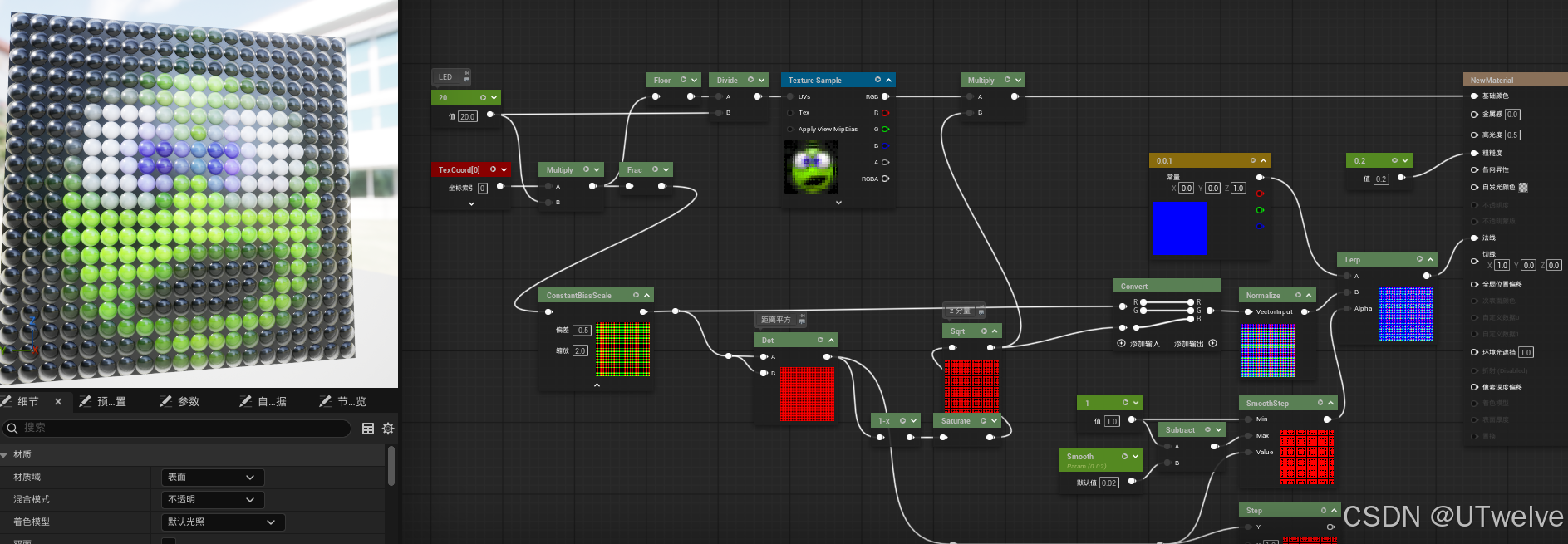
【UE】2D SphereNormalsMap - 实时计算2D “球形法线” 贴图
提示
本文介绍的是 2D 球形法线 的实时计算方法。
如果你在寻找 3D 球形法线 ,可以参考:
【UE5】在材质中实现球形法线技术,常用于改善植物等表面的渲染效果
为什么要用实时计算的球形法线?
在游戏开发中经常被当球踢的朋友都知道,球形法线贴图(Sphere Normal Map) 是一种被广泛使用的工具。
它不仅被用作圆形物体的表面法线,更是有着"真空下的球形鸡"般的图形学地位。
引擎附带一张现成的球形法线贴图,但它存在以下问题:
- 分辨率有限,放大后会产生像素化。
- 法线无法紧贴边缘,因为过于接近边界,会产生多种贴图问题。
- 自行烘培高精版本的成本较高(占用空间、生成时间长)。
因此,使用 实时计算 的方式有明显优势:
- 节省贴图资源:不占用额外的磁盘与显存空间,减少打包体积。
- 高精度结果:像素级精确计算,支持无损的任意缩放。
- 灵活可控:可根据实际需求修改形状、平滑程度、法线方向等参数。
SphereNormals 算法核心
算法思想非常简单:
将 UV 坐标映射到 [-1,1] 范围,得到球面上的二维投影位置,然后计算对应的 Z 分量以获得完整的球面法线。
公式:
z=1−saturate(u2+v2)z = \sqrt{1 - \text{saturate}(u^2 + v^2)} z=1−saturate(u2+v2)
最终法线向量:
n⃗=(u,v,z)\vec{n} = (u, v, z) n=(u,v,z)
💻 基础实现(Step 硬边版本)
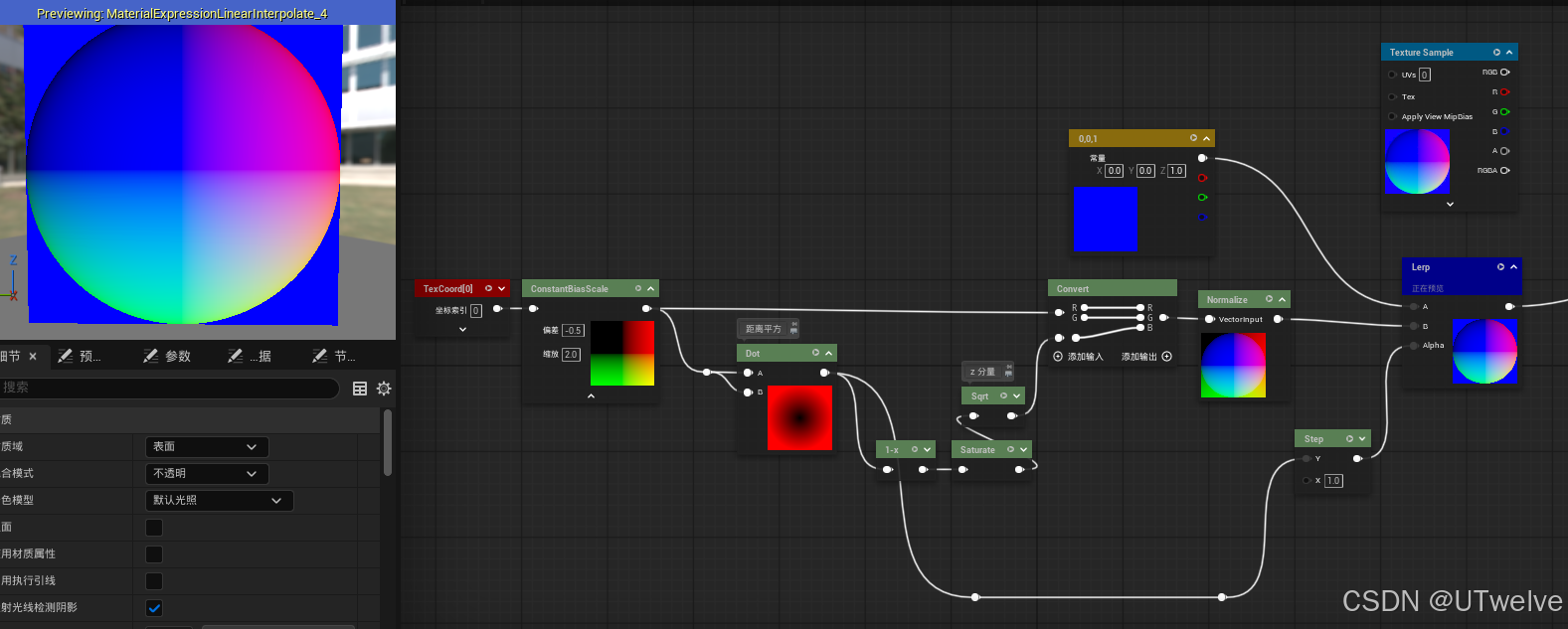
数学精确,法线严格满足球面公式,但由于计算十分精确、1:1对齐屏幕像素的输出、
在“圆的切线”与“屏幕像素排列”角度刁钻时,会出现锯齿状边缘的(摩尔纹的一种表现)
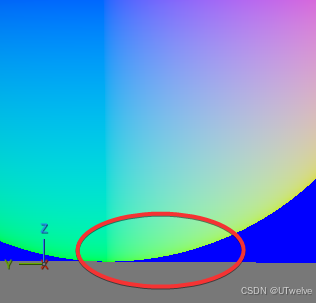
🌊 平滑版(Smoothstep 过渡)
消除硬边十分必要的话,可以使用Smoothstep代替Step,获得一个插值过渡,更适合视觉上柔和的效果
但!缺点是影响数学精度。如果此法线后续是用来参与进一步的数学计算的,那肯定不要选择使用Smoothstep平滑
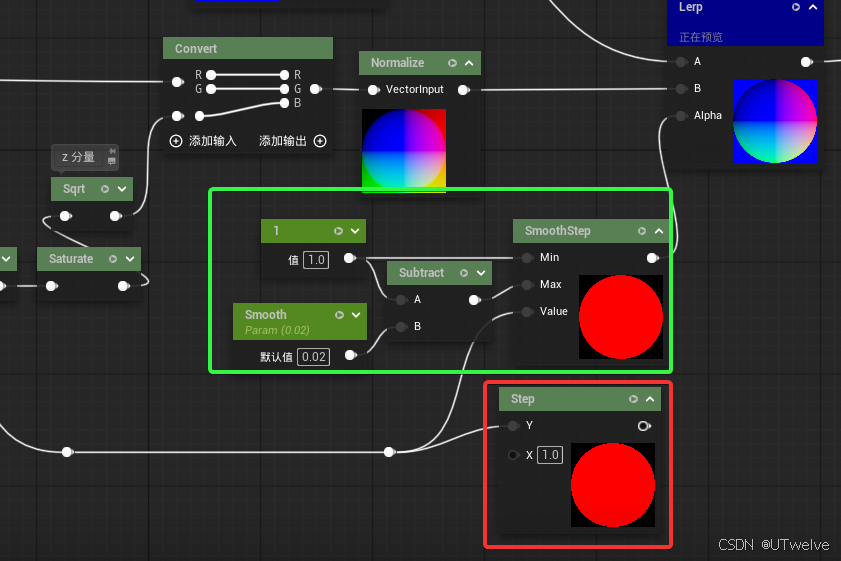
通过Smooth调整边缘平滑
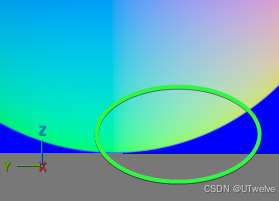
结果
这样一个快乐的2D球形法线就计算好了
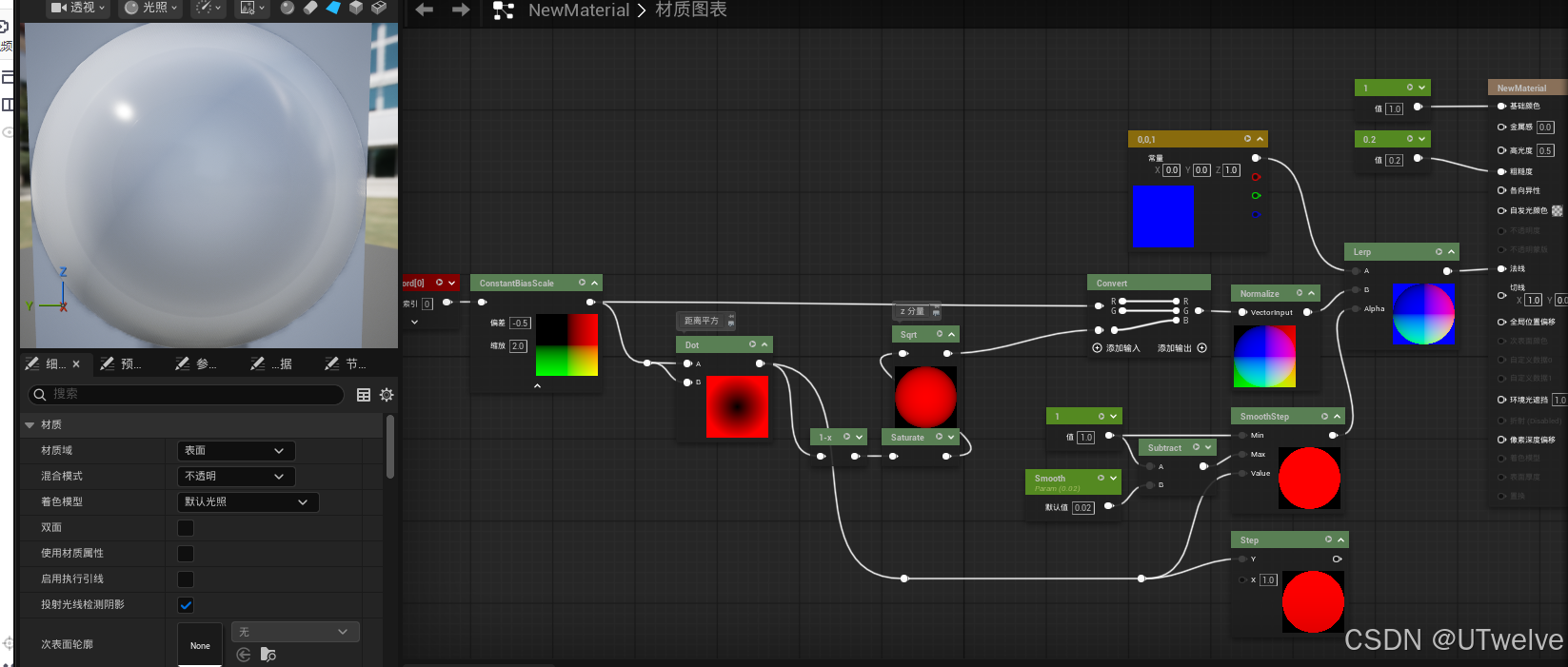
一些应用