Unity 三维数学方法
一.Vector3
(1) 叉积
public static Vector3 Cross(Vector3 lhs, Vector3 rhs)
输入:两个向量
lhs(左操作数)、rhs(右操作数)输出:一个新的
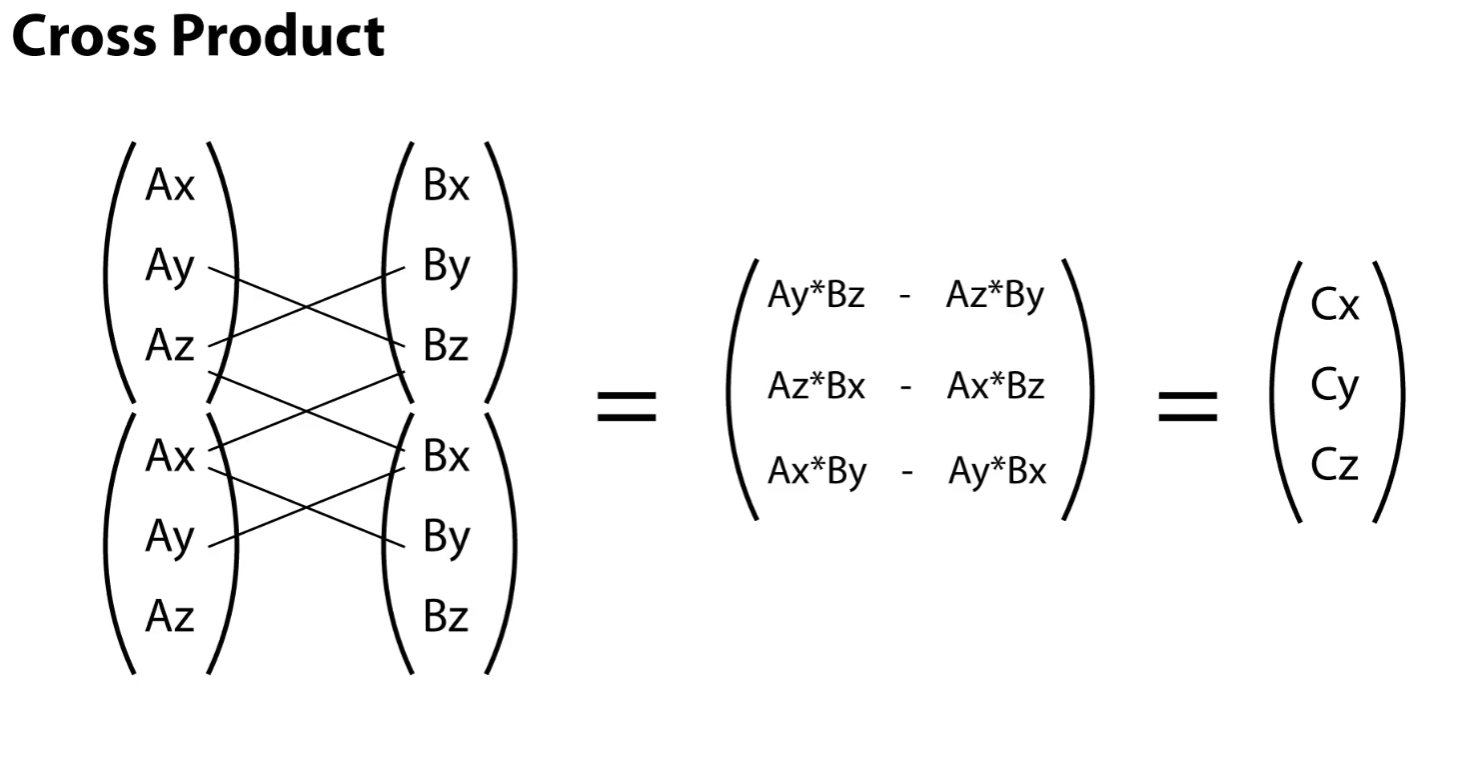
Vector3,它是这两个向量的叉积两个三维向量 叉积的结果是一个 垂直于这两个向量所在平面 的新向量。
长度:等于
|lhs| * |rhs| * sin(θ)其中 θ 是两个向量的夹角方向:我们使用左手,大拇指方向为lhs,食指方向为rhs,中指方向即结果的方向(因为unity是左手坐标系,所以我们使用左手,但是如果你查看一些数学文档会发现他们会让你使用右手)
(2) 点积
public static float Dot(Vector3 lhs, Vector3 rhs)
公式:Dot(a,b)=axbx+ayby+azbz
与夹角的关系:Dot(a,b)=∣a∣⋅∣b∣⋅cosθ

如果我们在求点积之前先将两向量归一化,那么点积就只等于 cosθ,范围在 [-1, 1],这时结果本身的大小也能量化两向量夹角,这很有用
(3)常见静态属性
| 属性 | 值 | 说明 |
|---|---|---|
Vector3.zero | (0,0,0) | 原点向量 |
Vector3.one | (1,1,1) | 每个分量都是 1 的向量 |
Vector3.right | (1,0,0) | X 轴正方向 |
Vector3.left | (-1,0,0) | X 轴负方向 |
Vector3.up | (0,1,0) | Y 轴正方向 |
Vector3.down | (0,-1,0) | Y 轴负方向 |
Vector3.forward | (0,0,1) | Z 轴正方向(Unity 左手坐标系:屏幕里) |
Vector3.back | (0,0,-1) | Z 轴负方向(Unity 左手坐标系:屏幕外) |
Vector3.positiveInfinity | (∞, ∞, ∞) | 所有分量正无穷大 |
Vector3.negativeInfinity | (-∞, -∞, -∞) | 所有分量负无穷大 |
(4)常见实例属性
| 属性 | 类型 | 说明 |
|---|---|---|
x, y, z | float | 向量的三个分量 |
magnitude | float | 向量的长度(√(x²+y²+z²)) |
sqrMagnitude | float | 向量长度的平方(效率更高,避免开方运算) |
normalized | Vector3 | 单位化向量(方向相同,长度为 1) |
(5)public static Vector3 ClampMagnitude(Vector3 vector, float maxLength)
把一个向量的长度限制在不超过 maxLength
参数
vector:输入的向量。
maxLength:允许的最大模长(长度)。
返回值
一个新的向量。
如果
vector的长度小于等于maxLength,返回原向量。如果
vector的长度大于maxLength,返回一个方向相同但长度为maxLength的向量。
(6)public static Vector3 ProjectOnPlane(Vector3 vector, Vector3 planeNormal)
把一个向量投影到某个平面上。
vector:要投影的向量。planeNormal:平面的法线(垂直于平面的方向)
返回值:
投影后的新向量(位于平面内,方向是
vector在平面上的分量)。
二.Quaternion
(1) public static Quaternion Euler(Vector3 euler)
欧拉角代表一个旋转,将该旋转转换为四元数,沿欧拉角的z旋转z度,然后是x,最后是y
(2)public static Quaternion LookRotation(Vector3 forward, Vector3 upwards)
Quaternion.LookRotation 用来创建一个旋转四元数,使得物体的 前方向(Z 轴方向)对准 forward,并且用 upwards 来指定物体的“头顶”方向。
典型用途是:让一个物体“朝向”某个方向。
参数解释
forward目标前方向(世界坐标或局部计算出来的向量)
必须是 非零向量
upwards(可选,默认Vector3.up)用来指定旋转后的物体的“上方向”。
通常用默认的
(0,1,0),即世界的 Y 轴正方向。
Quaternion.LookRotation(forward, upwards) = 生成一个旋转,使得物体的 Z 轴对准 forward,并且 Y 轴尽量贴合 upwards。
三.Mathf
(1) public static float Exp(float power);
计算 e 的 x 次方,即 指数函数。e 是自然对数的底数,约等于 2.71828,而 x 是你传入的参数
