当前位置：首页 > news >正文

权重衰减与暂退法

news 2025/9/11 9:48:41

为什么需要权重衰减

机器学习模型如果参数值过大，容易在训练数据上拟合得过好，进而对测试或新数据表现不佳。这就是所谓的“过拟合”。通过对参数进行适度惩罚，可以让模型更简洁、更稳健。

L2 正则化通过加入参数平方和的惩罚项，使得训练过程中模型尽量保持较小的权值，有助于泛化性能。

L2 范数

对于权重向量 $\mathbf{w} = [w_1, w_2, ..., w_n]$ ，其 L2 范数定义为： $\|\mathbf{w}\|_2 = \sqrt{\sum_{i} w_i^2}$
为简化计算，通常使用平方后的 L2 范数： $\|\mathbf{w}\|_2^2 = \sum_{i} w_i^2$ 这样避免平方根操作，方便求导。

权重衰减（L2 正则化）

通过损失函数加入惩罚项： $L_{\text{new}} = L_{\text{original}} + \frac{\lambda}{2} \sum_i w_i^2$ 将原来的训练目标最小化训练标签上的预测损失，调整为最小化预测损失和惩罚项之和。

其中 $\lambda$ 是正则化系数，控制惩罚强度；添加 $\tfrac12$ 是为了求导时方便。

在使用 SGD 时，L2 正则化与权重衰减等价。原理是惩罚项导数会导致每次更新中权重按比例缩小，就像“衰减”了一样。

代码实现

%matplotlib inline
import torch
from torch import nn
from d2l import torch as d2ln_train, n_test, num_inputs, batch_size = 20, 100, 200, 5
true_w, true_b = torch.ones((num_inputs, 1)) * 0.01, 0.05
train_data = d2l.synthetic_data(true_w, true_b, n_train)
train_iter = d2l.load_array(train_data, batch_size)
test_data = d2l.synthetic_data(true_w, true_b, n_test)
test_iter = d2l.load_array(test_data, batch_size, is_train=False)def init_params():w = torch.normal(0, 1, size=(num_inputs, 1), requires_grad=True)b = torch.zeros(1, requires_grad=True)return [w, b]def l2_penalty(w):return torch.sum(w.pow(2)) / 2def train(lambd):w, b = init_params()net, loss = lambda X: d2l.linreg(X, w, b), d2l.squared_lossnum_epochs, lr = 100, 0.003animator = d2l.Animator(xlabel='epochs', ylabel='loss', yscale='log',xlim=[5, num_epochs], legend=['train', 'test'])for epoch in range(num_epochs):for X, y in train_iter:# 增加了L2范数惩罚项，# 广播机制使l2_penalty(w)成为一个长度为batch_size的向量l = loss(net(X), y) + lambd * l2_penalty(w)l.sum().backward()d2l.sgd([w, b], lr, batch_size)if (epoch + 1) % 5 == 0:animator.add(epoch + 1, (d2l.evaluate_loss(net, train_iter, loss),d2l.evaluate_loss(net, test_iter, loss)))print('w的L2范数是：', torch.norm(w).item())train(lambd=0)train(lambd=3)

代码整体流程

造数据
- 用 D2L 生成高维（200 特征）、小样本（20 训练、100 测试）的线性回归数据。
- 真实权重很小（0.01），容易过拟合。
定义工具
- init_params() 初始化参数。
- l2_penalty(w) 定义 L2 范数惩罚。
训练函数 train(lambd)
- 构建线性模型 + 平方损失。
- 在每个 batch 的损失中加入 λ * ½‖w‖²。
- 用 SGD 更新参数，并记录训练/测试损失曲线。
- 最后输出权重的 L2 范数。
实验对比
- train(0)：无正则，训练损失低但过拟合，权重范数大。
- train(3)：加正则，权重被压小，测试损失更稳健，泛化更好。

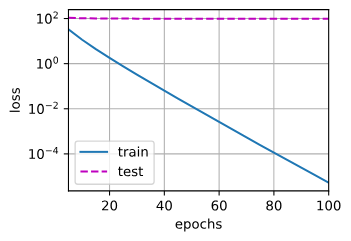
无权重衰减

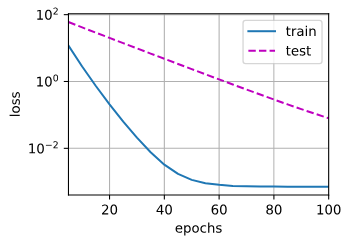
有权重衰减

权重衰减部分代码

def l2_penalty(w):
return torch.sum(w.pow(2)) / 2

这里实现了 L2 惩罚： $\tfrac12 \sum w_i^2$ 。
除以 2 只是数学上方便求导，导数刚好是 $w$ 。

l = loss(net(X), y) + lambd * l2_penalty(w)

loss(net(X), y)：常规平方损失（逐样本）。
lambd * l2_penalty(w)：额外的正则项，不依赖输入数据，只依赖参数 w。
二者相加后，就形成了“带权重衰减的损失函数”。

l.sum().backward()

由于前面 loss 返回的是按样本的向量，正则项会被广播到每个样本。
.sum() 把所有样本的损失 + 正则项求和，再反向传播。
在反向传播时，正则项对 w 的梯度贡献就是 $\lambda w$ ，这就是“权重衰减”的来源。

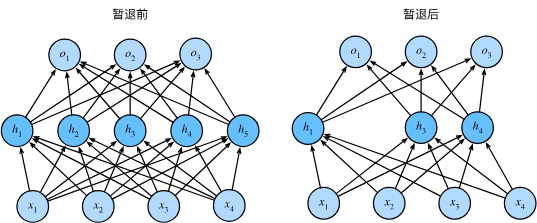
什么是暂退法（Dropout）？

暂退法是一种在训练过程中随机“丢弃”部分神经元（通常是隐藏层）的技术，通过这种随机剔除来降低网络对特定节点的依赖，有助于破坏神经元之间的“共适应性”，减少过拟合，提高模型的泛化能力。

原理：带无偏缩放的随机剔除

在每次训练的前向传播中，以概率 $p$ 将某些神经元置为 0（即被“暂退”），其他保留的神经元则按比例 $1/(1-p)$ 缩放输出。这种处理确保了每层输出的期望保持不变，从而不会改变网络整体的行为分布：

$h' = \begin{cases} 0, & \text{with probability } p,\\ \displaystyle\frac{h}{1-p}, & \text{with probability } 1-p. \end{cases}$

何时使用暂退法？

训练阶段：使用 Dropout，随机丢弃部分节点，并缩放保留节点的输出。
推理（测试）阶段：通常不使用 Dropout（即不会丢弃节点，也不进行缩放），直接使用全网络进行前向传播。这样做确保了输出的稳定性，同时由于训练时已缩放过，推理时输出期望仍然一致。
有些研究会在推理过程中使用 Dropout 多次采样，以估计模型输出的不确定性：通过多次随机 Dropout，观察输出变化的稳定性，判断模型预测的可信度。

暂退法简洁代码实现：

import torch
import torch.nn as nn
import torch.optim as optim
from torchvision import datasets, transforms
from torch.utils.data import DataLoader# 数据准备（以 Fashion-MNIST 为例）
transform = transforms.Compose([transforms.ToTensor(),transforms.Normalize((0.5,), (0.5,))
])
train_loader = DataLoader(datasets.FashionMNIST(root='./data', train=True, download=True, transform=transform),batch_size=128, shuffle=True
)
test_loader = DataLoader(datasets.FashionMNIST(root='./data', train=False, download=True, transform=transform),batch_size=128, shuffle=False
)# 使用 Sequential 构建网络
model = nn.Sequential(nn.Flatten(),nn.Linear(28 * 28, 256),nn.ReLU(),nn.Dropout(0.3),         # Dropout 概率为 0.3nn.Linear(256, 128),nn.ReLU(),nn.Dropout(0.5),         # 第二层 Dropout 概率为 0.5nn.Linear(128, 10)
)device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
model.to(device)criterion = nn.CrossEntropyLoss()
optimizer = optim.Adam(model.parameters(), lr=0.001)# 训练和测试函数
def train_epoch():model.train()total_loss = total_correct = total_samples = 0for X, y in train_loader:X, y = X.to(device), y.to(device)optimizer.zero_grad()outputs = model(X)loss = criterion(outputs, y)loss.backward()optimizer.step()total_loss += loss.item() * X.size(0)_, predicted = outputs.max(1)total_correct += predicted.eq(y).sum().item()total_samples += X.size(0)return total_loss / total_samples, total_correct / total_samplesdef evaluate():model.eval()total_loss = total_correct = total_samples = 0with torch.no_grad():for X, y in test_loader:X, y = X.to(device), y.to(device)outputs = model(X)loss = criterion(outputs, y)total_loss += loss.item() * X.size(0)_, predicted = outputs.max(1)total_correct += predicted.eq(y).sum().item()total_samples += X.size(0)return total_loss / total_samples, total_correct / total_samples# 训练过程
num_epochs = 10
for epoch in range(1, num_epochs + 1):train_loss, train_acc = train_epoch()test_loss, test_acc = evaluate()print(f"Epoch {epoch}/{num_epochs} — "f"Train: loss={train_loss:.4f}, acc={train_acc:.4f} | "f"Test: loss={test_loss:.4f}, acc={test_acc:.4f}")

关键部分：

# 使用 Sequential 构建网络
model = nn.Sequential(
nn.Flatten(),
nn.Linear(28 * 28, 256),
nn.ReLU(),
nn.Dropout(0.3), # Dropout 概率为 0.3
nn.Linear(256, 128),
nn.ReLU(),
nn.Dropout(0.5), # 第二层 Dropout 概率为 0.5
nn.Linear(128, 10)
)

只需在每个全连接层之后添加一个Dropout层，将暂退概率作为唯一的参数传递给它的构造函数。在训练时，Dropout层将根据指定的暂退概率随机丢弃上一层的输出（相当于下一层的输入）。在测试时，Dropout层仅传递数据。