当前位置：首页 > news >正文

栈：逆波兰表达式求解

news 2025/9/11 5:35:11

什么是前缀表达式（波兰式）

运算符位于数之前。

比如：

10+2 对应前缀表达式是 + 10 2

(4 + (13 / 5)) 对应前缀表达式是 + 4 / 13 5

什么是中缀表达式

我们常用的算数表达式。比如 (4 + (13 / 5))，人类很容易计算出来，但计算机需要进行优先级比较，所以计算机更偏向于前缀或者后缀表达式。

什么是后缀表达式（逆波兰式）

运算符位于数之后。

比如：

10+2 对应的后缀表达式是 10 2 +

(4 + (13 / 5)) 对应的后缀表达式是 4 13 5 / +

计算思路

类型	示例	计算方式
前缀表达式	+ 4 / 13 5	从右往左读，压入栈中
中缀表达式	(4 + (13 / 5))	考虑优先级
后缀表达式	4 13 5 / +	从左往右读，压入栈中

求解逆波兰表达式

题目描述：给一个逆波兰表达式字符串，求解并返回。

注意：

有效的算符为 '+'、'-'、'*' 和 '/' 。
每个操作数（运算对象）都可以是一个整数或者另一个表达式。
两个整数之间的除法总是 向零截断 。
表达式中不含除零运算。
输入是一个根据逆波兰表示法表示的算术表达式。
答案及所有中间计算结果可以用 32 位 整数表示。

示例：

输入：tokens = ["4","13","5","/","+"]
输出：6
解释：该算式转化为常见的中缀算术表达式为：(4 + (13 / 5)) = 6

求解思路：利用栈

class Solution {public int evalRPN(String[] tokens) {Deque<Integer> deque = new ArrayDeque<>();for (int i = 0; i < tokens.length; i++) {if (isOprate(tokens[i])) {int num2 = deque.pop();int num1 = deque.pop();int re = calculate(num1, num2, tokens[i]);deque.push(re);} else {deque.push(Integer.parseInt(tokens[i]));}}return deque.pop();}//操作符判断public boolean isOprate(String str) {return "+".equals(str) || "-".equals(str) || "*".equals(str) || "/".equals(str);}//计算public int calculate(int num1, int num2, String op) {int res = 0;switch (op) {case "+":res = num1 + num2;break;case "-":res = num1 - num2;break;case "*":res = num1 * num2;break;case "/":res = num1 / num2;break;default:break;}return res;}
}

求解波兰表达式

public class Prefix {// 前缀表达式（波兰式）求解public int prefix(String[] tokens) {Deque<Integer> stack = new ArrayDeque<>();for (int i = tokens.length - 1; i >= 0; i--) { //从后往前遍历if (isOperator(tokens[i])) {int num2 = stack.pop();int num1 = stack.pop();stack.push(calculate(num1, num2, tokens[i]));} else {stack.push(Integer.parseInt(tokens[i]));}}return stack.pop();}// 操作符判断public boolean isOperator(String op) {return "+".equals(op) || "-".equals(op) || "*".equals(op) || "/".equals(op);}// 计算public int calculate(int num1, int num2, String op) {switch (op) {case "+":return num1 + num2;case "-":return num1 - num2;case "*":return num1 * num2;case "/":return num1 / num2;default:}return 0;}public static void main(String[] args) {String[] tokens = {"+", "4", "/", "15", "5"};//4+15/5System.out.println(new Prefix().prefix(tokens));}
}

求解中缀表达式：中缀转后缀-》再后缀求解

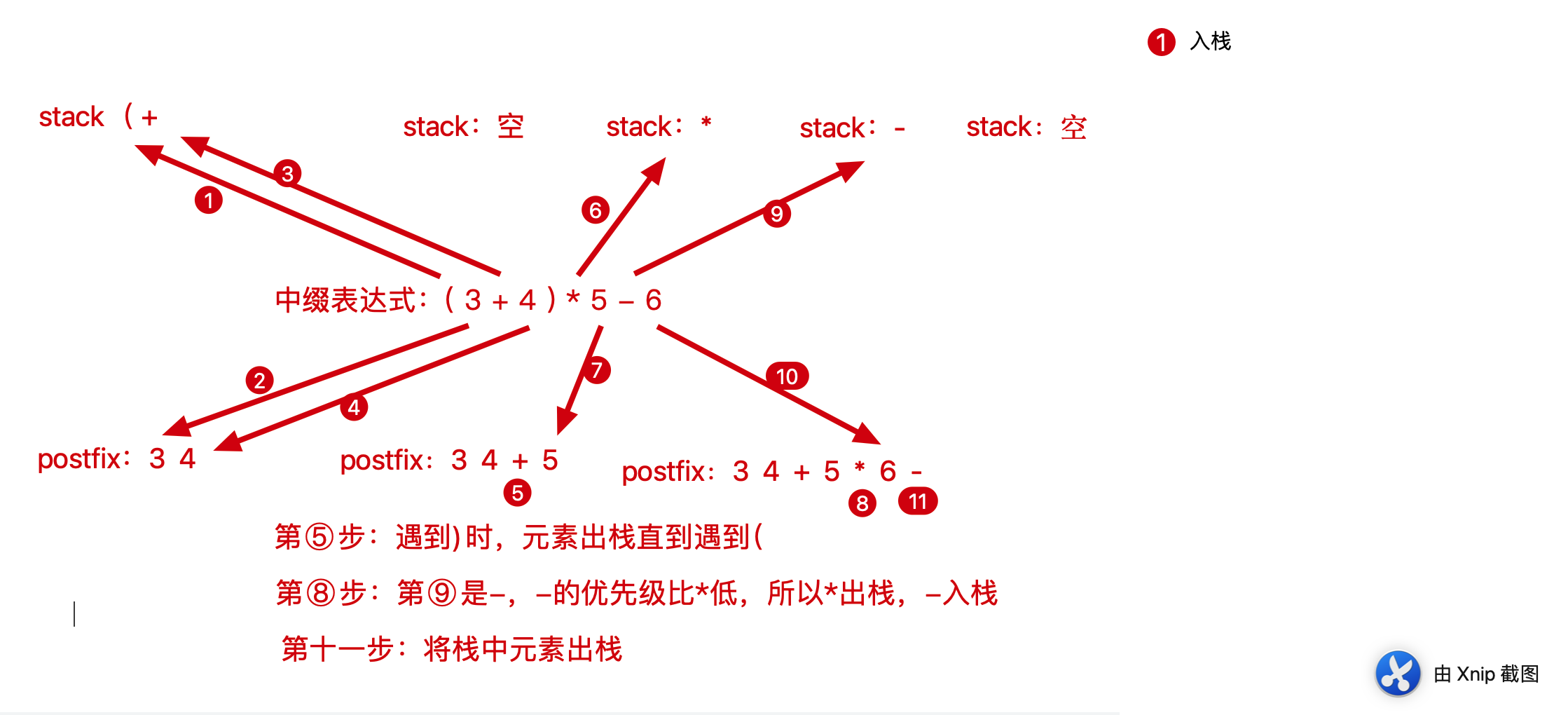
中缀转后缀的过程：

数字：后缀表达式元素+1。
遇到 ( 左括号：压入栈中。
遇到 ) 右括号：将栈中的元素弹出作为后缀表达式的元素，直到遇到左括号(，再把左括号弹出。
遇到操作符：当前操作符和栈中的操作符比较优先级，优先级高的作为后缀表达式一员，优先级低的入栈。

public class Infix {private static final Map<String, Integer> PRECEDENCE = new HashMap<>();static {PRECEDENCE.put("+", 1);PRECEDENCE.put("-", 1);PRECEDENCE.put("*", 2);PRECEDENCE.put("/", 2);PRECEDENCE.put("^", 3);}// 中缀表达式转后缀表达式public String[] infixToPostfix(String[] tokens) {// 栈用来存放表达式Deque<String> stack = new ArrayDeque();// 后缀表达式StringBuilder postfix = new StringBuilder();for (int i = 0; i < tokens.length; i++) {String token = tokens[i];if (isNumber(token)) {  // 是数字postfix.append(token).append(" ");} else if ("(".equals(token)) {  // 是左括号(stack.push(token);} else if (")".equals(token)) {  // 是右括号）while (!stack.isEmpty() && !"(".equals(stack.peek())) {postfix.append(stack.pop()).append(" ");}stack.pop();} else if (isOperator(token)) {  // 是操作符while (!stack.isEmpty() && isOperator(stack.peek()) &&hasHigherPrecedence(stack.peek(), token)) {postfix.append(stack.pop()).append(" ");}stack.push(token);}}return postfix.toString().split(" ");}// 优先级比较public boolean hasHigherPrecedence(String op1, String op2) {return PRECEDENCE.get(op1) >= PRECEDENCE.get(op2);}// 判断是不是数字private static boolean isNumber(String token) {try {Integer.parseInt(token);return true;} catch (NumberFormatException e) {return false;}}private static boolean isOperator(String token) {return PRECEDENCE.containsKey(token);}public static void main(String[] args) {String infix = "( 3 + 4 ) * 5 - 6";String[] postfix = new Infix().infixToPostfix(infix.split(" "));System.out.println("Infix to Postfix: " + Arrays.toString(postfix));}
}

练习地址：https://leetcode.cn/problems/evaluate-reverse-polish-notation/description/