动态规划篇(背包问题)
目录
一、01背包问题
二、完全背包问题
三、对比01背包和完全背包核心代码
四、多重背包问题Ⅰ
编辑 五、多重背包问题Ⅱ
编辑 六、分组背包问题
一、01背包问题

#include<bits/stdc++.h>using namespace std;const int MAXN = 1005;
int v[MAXN]; // 体积
int w[MAXN]; // 价值
int f[MAXN][MAXN]; // f[i][j], j体积下前i个物品的最大价值 int main()
{int n, m; cin >> n >> m;for(int i = 1; i <= n; i++) cin >> v[i] >> w[i];for(int i = 1; i <= n; i++) for(int j = 1; j <= m; j++){// 当前背包容量装不进第i个物品,则价值等于前i-1个物品if(j < v[i]) f[i][j] = f[i - 1][j];// 能装,需进行决策是否选择第i个物品else f[i][j] = max(f[i - 1][j], f[i - 1][j - v[i]] + w[i]);} cout << f[n][m] << endl;return 0;
}
代码优化
include<bits/stdc++.h>using namespace std;const int MAXN = 1005;
int f[MAXN]; // int main()
{int n, m; cin >> n >> m;for(int i = 1; i <= n; i++) {int v, w;cin >> v >> w; // 边输入边处理for(int j = m; j >= v; j--)f[j] = max(f[j], f[j - v] + w);}cout << f[m] << endl;return 0;
}讲解:



二、完全背包问题

动态规划解题步骤
动态规划问题一般从三个步骤进行考虑。
步骤一:集合和集合的状态
所谓的集合,就是一些方案的集合。
用 g[i][j] 表示从前 i 种物品中进行选择,且总体积不大于 j 的各个选法获得的价值的集合。注意:g[i][j] 不是一个数,是一堆数。
例如 g[2][3] 从前 2 种物品中进行选择,且总体积不大于 3 的各个选法获得的价值的集合。
g[2][3] 的可选择方案包括:
方案一:都不选,总价值为 0。
方案二:选 1 件 物品 1,总价值为 2。
方案三:选 2 件物品 1,总价值为 4。
方案四:选 3件 物品 1,总价值为 6。
方案五:选 1 件物品 2,总价值为 4。
方案六:选 1 件物品 2,一件物品 1,总价值为 6。
所以 g[2][3] = {0,2,4,6,4,2}。
i j 取不同的值,对应不同的 g[i][j],也就是对应不同的集合。
用 f[i][j] 表示从前 i 种物品中进行选择,总体积小于等于 j 所能获得的最大价值。很明显,f[i][j] 就是 g[i][j] 中的最大值。i j 取不同的值,就对应不同的 f[i][j]。我们把 f[i][j] 叫做集合的状态。
例如 f[2][3] 表示从前 2 种物品中进行选择,且总体积不大于 3 的获得的最大价值。f[2][3] = max(g[2][3] ) = max( 0,2,4,6,4,2) = 6。
g[i][j] 的最大值就是 f[i][j]。
如果我们能把所有集合对应的最大值都求出来,即求出了 f[0][0] ~ f[N][V], f[N][V] 的含义是在前 N 种物品中进行选择,总体积不大于 V 所获得的最大价值,就是我们要找的答案。
注意,我们不需要把各个集合的所有元素都找出来,只需要求出各个集合的最大值,就能找到答案。下面就是如何求出各个集合的最大值。
步骤二:状态计算
g[i][j] 是从前 i 种物品中进行选择,且总体积不大于 j 的各个选法获得的价值的集合。
f[i][j] 是从前 i 种物品中进行选择,总体积小于等于 j 所能获得的最大价值。
f[i][j] 是集合 g[i][j] 的最大值。

所谓的状态计算是指,如何将把 f[i][j] 算出来。
如果把各个集合 g[i][j] 的状态 f[i][j] 求出来, f[N][V] 就是要找的答案。
回想一下 0 1 背包问题。
01 背包问题把 g[i][j]划分成了 A B 两部分,分别求出这两个部分对应的最大值,然后两者取最大值就是整体 g[i][j] 的最大值,就是 f[i][j]。
01 背包根据是否选择第 i 件物品,也就是第 i 件物品选 0 个还是 1 个,把 g[i][j] 划分成了 A B 两部分,分别求出这两个部分的最大值,然后两者取最大值就是整体 g[i][j] 的最大值,也就求出了 f[i][j]。
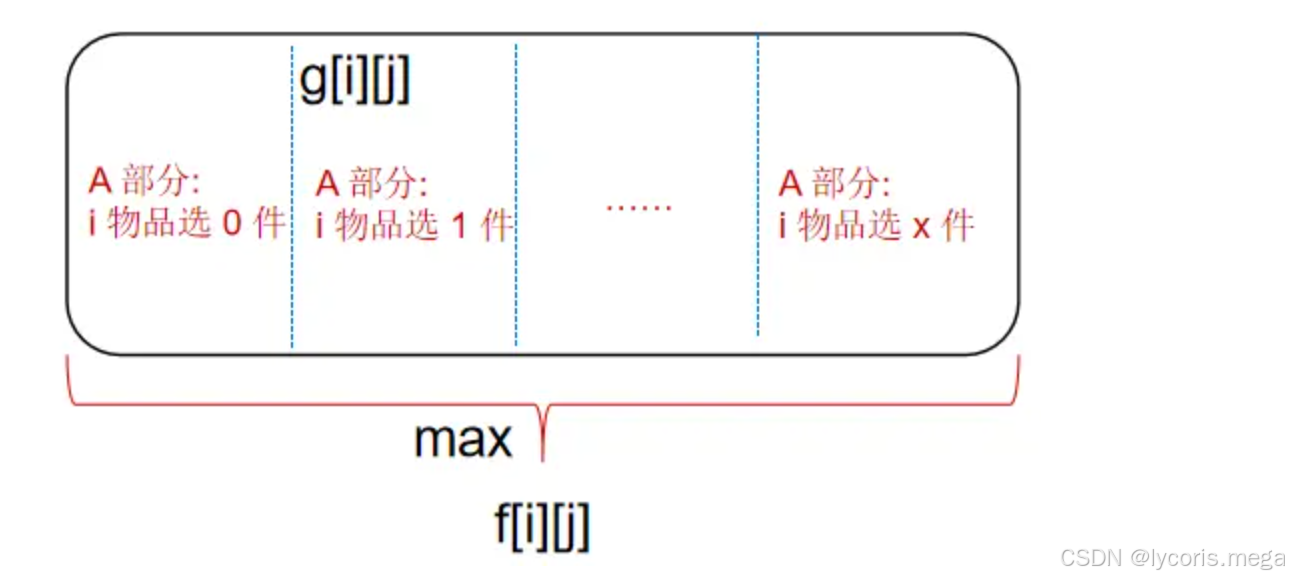
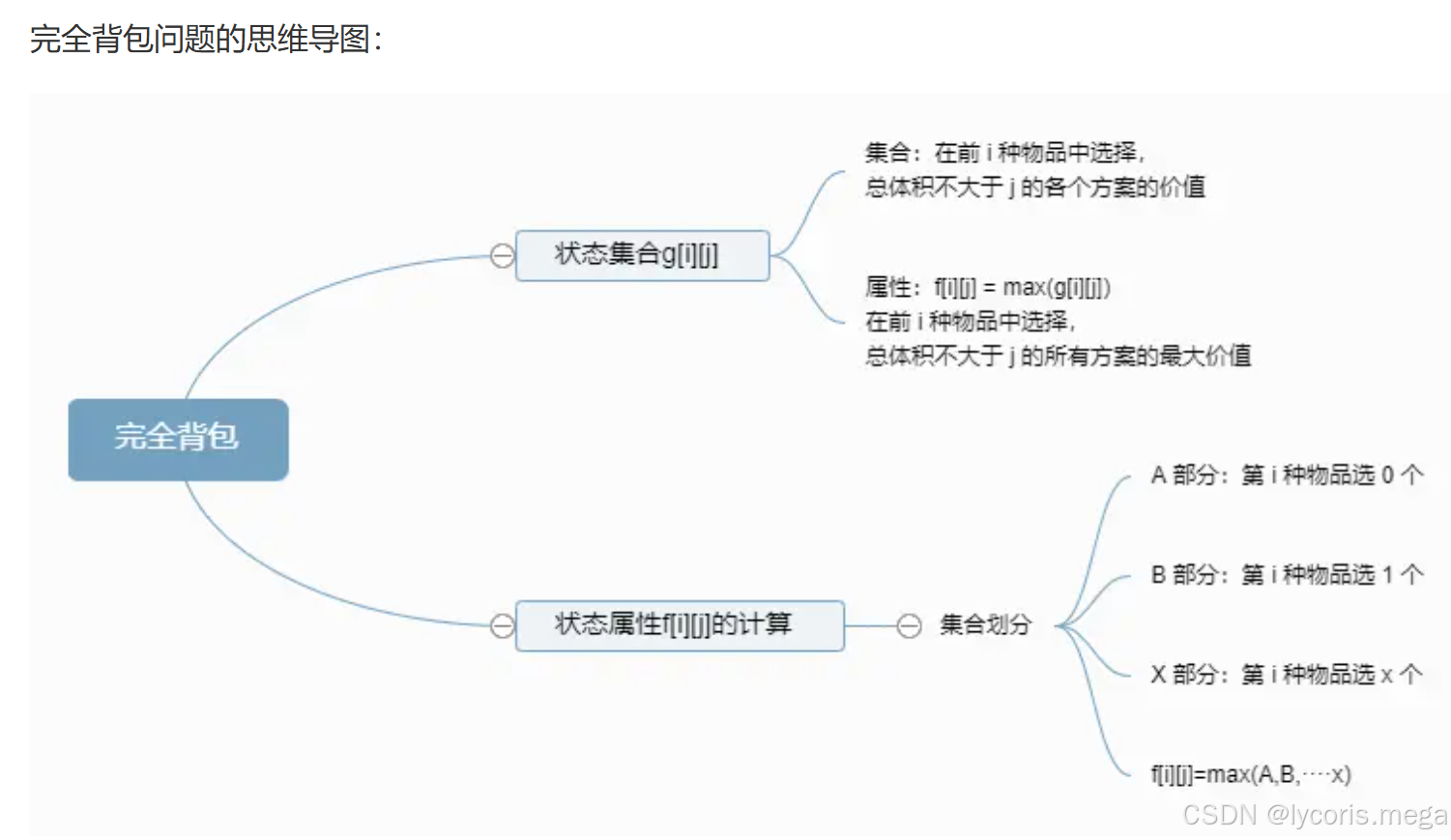
完全背包问题也是根据第 i 件物品的选择数量,把 g[i][j] 划分成不同的部分,分别求出各个部分的最大值,取各个部分最大值中的最大值,就是整体 g[i][j] 的最大值,也就求出了 f[i][j]。
因为每种物品的数量是无限的,根据第 i 种物品的选择数量可以把 g[i][j] 分为这样几部分:
A 部分: 第 i 种物品选 0 件。
B 部分:第 i 件物品选 1 件。
C 部分: 第 i 件物品选 2 件。
X 部分: 第 i 件物品选 x 件。
. . . . .



#include<iostream>
using namespace std;const int N = 1010;int n, m;
int f[N][N], v[N], w[N];int main(){cin >> n >> m;for(int i = 1; i <= n; i ++ )cin >> v[i] >> w[i];for(int i = 0; i <= m; i++)//初始化{f[0][i] = 0;}for(int i = 1; i <= n; i ++ )for(int j = 0; j <= m; j ++ )for(int k = 0; k * v[i] <= j; k ++ )f[i][j] = max(f[i][j], f[i - 1][j - k * v[i]] + k * w[i]);//求出每一个 f[i][j]cout << f[n][m] << endl;
} 



for(int i = 1; i <= n; i ++ ){for(int j = 0; j <= m; j ++ ){if(v[i] <= j)//第 i 种能放进去f[i][j] =max(f[i - 1][j], f[i][j - v[i]] + w[i]);else//如果第 i 件物品不能放进去f[i][j] = f[i - 1][j];}}#include<iostream>
using namespace std;const int N = 1010;int n, m;
int f[N][N], v[N], w[N];int main()
{cin >> n >> m;for(int i = 1; i <= n; i ++ )cin >> v[i] >> w[i];for(int i = 1; i <= n; i ++ ){for(int j = 0; j <= m; j ++ ){if(v[i] <= j)f[i][j] =max(f[i - 1][j], f[i][j - v[i]] + w[i]);elsef[i][j] = f[i - 1][j];}}cout << f[n][m] << endl;
}三、对比01背包和完全背包核心代码
f[i][j] = max(f[i][j],f[i-1][j-v[i]]+w[i]);//01背包f[i][j] = max(f[i][j],f[i][j-v[i]]+w[i]);//完全背包问题 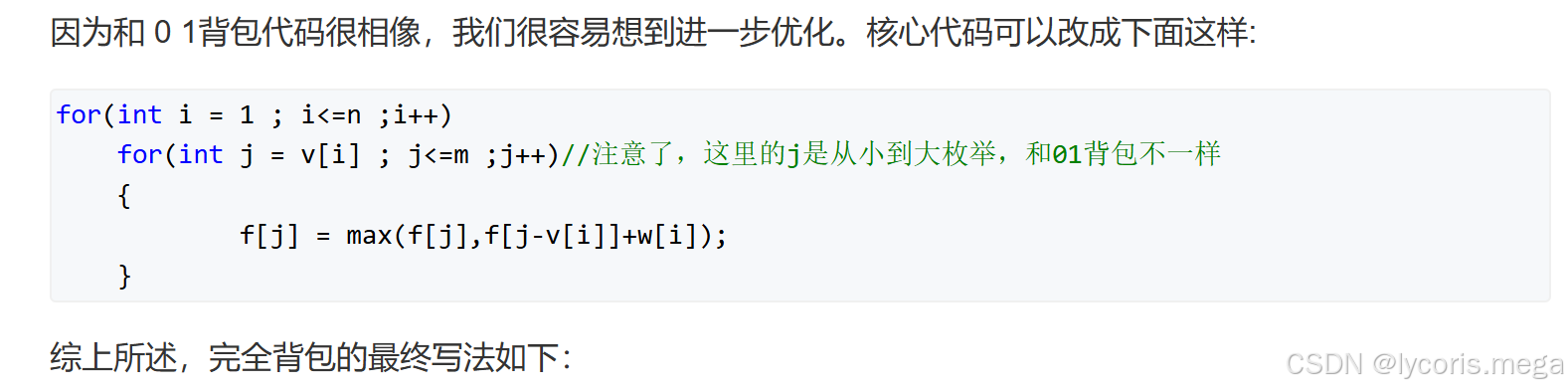
#include<iostream>
using namespace std;
const int N = 1010;
int f[N];
int v[N],w[N];
int main()
{int n,m;cin>>n>>m;for(int i = 1 ; i <= n ;i ++){cin>>v[i]>>w[i];}for(int i = 1 ; i<=n ;i++)for(int j = v[i] ; j<=m ;j++){f[j] = max(f[j],f[j-v[i]]+w[i]);}cout<<f[m]<<endl;
} 
四、多重背包问题Ⅰ


#include <bits/stdc++.h>
using namespace std;
int a[10005],b[10005],t=0,n,m,dp[10005]={ },w,v,s;
int main()
{cin>>n>>m;while(n--){cin>>v>>w>>s;while(s--){a[++t]=v;b[t]=w;}//死拆,把多重背包拆成01背包}for(int i=1;i<=t;i++)for(int j=m;j>=a[i];j--)dp[j]=max(dp[j-a[i]]+b[i],dp[j]);//直接套01背包的板子cout<<dp[m]<<endl;return 0;
}优化
#include <bits/stdc++.h>
using namespace std;
int dp[1005],n,t,v,w,s;
main()
{cin>>n>>t;while(n--){cin>>w>>v>>s;while(s--)for(int j=t;j>=w;j--)dp[j]=max(dp[j],dp[j-w]+v);}cout<<dp[t];
}


 五、多重背包问题Ⅱ
五、多重背包问题Ⅱ

#include<iostream>
using namespace std;const int N = 12010, M = 2010;int n, m;
int v[N], w[N]; //逐一枚举最大是N*logS
int f[M]; // 体积<Mint main()
{cin >> n >> m;int cnt = 0; //分组的组别for(int i = 1;i <= n;i ++){int a,b,s;cin >> a >> b >> s;int k = 1; // 组别里面的个数while(k<=s){cnt ++ ; //组别先增加v[cnt] = a * k ; //整体体积w[cnt] = b * k; // 整体价值s -= k; // s要减小k *= 2; // 组别里的个数增加}//剩余的一组if(s>0){cnt ++ ;v[cnt] = a*s; w[cnt] = b*s;}}n = cnt ; //枚举次数正式由个数变成组别数//01背包一维优化for(int i = 1;i <= n ;i ++)for(int j = m ;j >= v[i];j --)f[j] = max(f[j],f[j-v[i]] + w[i]);cout << f[m] << endl;return 0;
} 
 六、分组背包问题
六、分组背包问题

#include<bits/stdc++.h>
using namespace std;const int N=110;
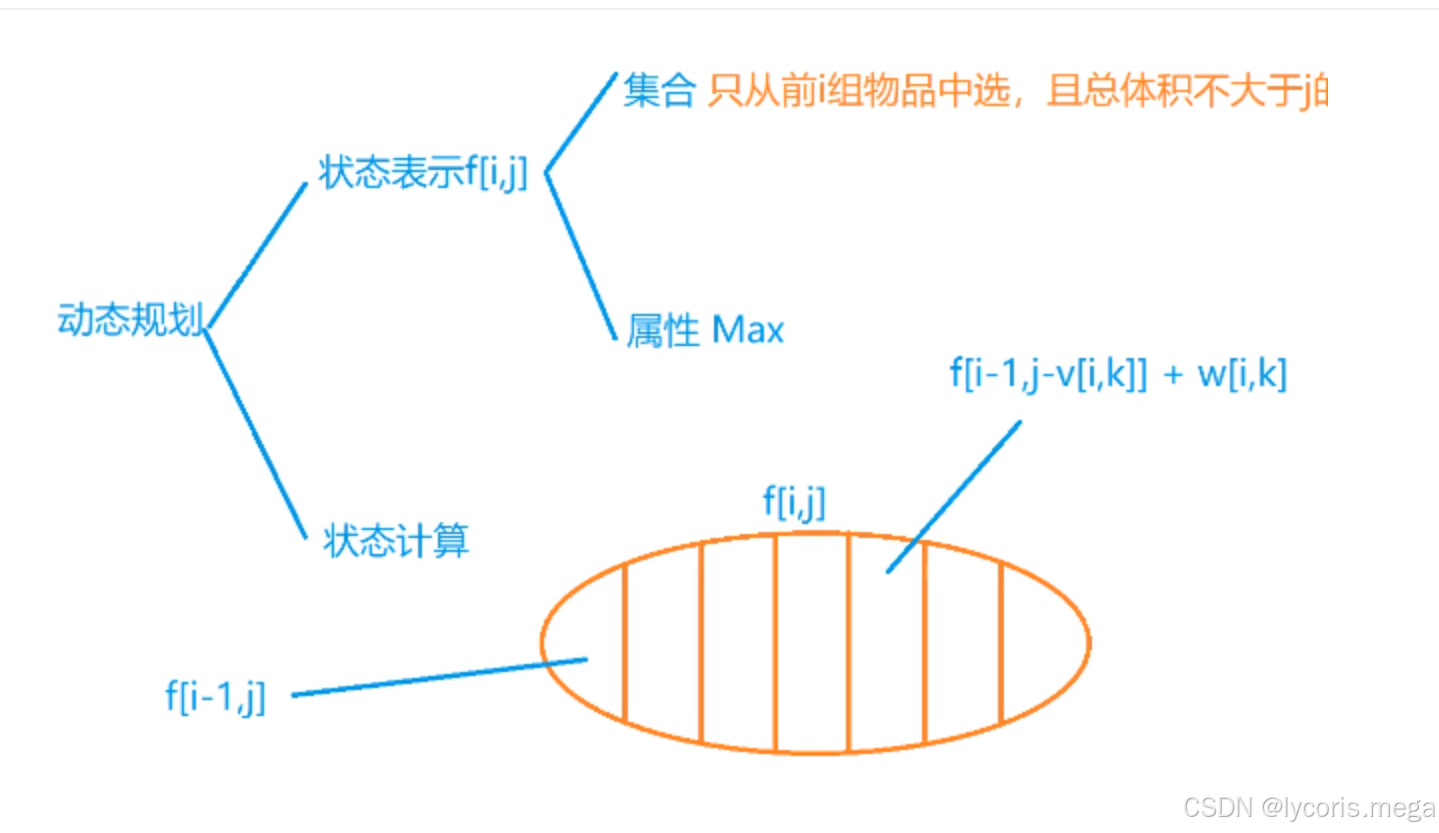
int f[N][N]; //只从前i组物品中选,当前体积小于等于j的最大值
int v[N][N],w[N][N],s[N]; //v为体积,w为价值,s代表第i组物品的个数
int n,m,k;int main(){cin>>n>>m;for(int i=1;i<=n;i++){cin>>s[i];for(int j=0;j<s[i];j++){cin>>v[i][j]>>w[i][j]; //读入}}for(int i=1;i<=n;i++){for(int j=0;j<=m;j++){f[i][j]=f[i-1][j]; //不选for(int k=0;k<s[i];k++){if(j>=v[i][k]) f[i][j]=max(f[i][j],f[i-1][j-v[i][k]]+w[i][k]); }}}cout<<f[n][m]<<endl;
}
因为只用到了第i-1列,所以可以仿照01背包的套路逆向枚举体积
#include<bits/stdc++.h>
using namespace std;const int N=110;
int f[N];
int v[N][N],w[N][N],s[N];
int n,m,k;int main(){cin>>n>>m;for(int i=0;i<n;i++){cin>>s[i];for(int j=0;j<s[i];j++){cin>>v[i][j]>>w[i][j];}}for(int i=0;i<n;i++){for(int j=m;j>=0;j--){for(int k=0;k<s[i];k++){ //for(int k=s[i];k>=1;k--)也可以if(j>=v[i][k]) f[j]=max(f[j],f[j-v[i][k]]+w[i][k]); }}}cout<<f[m]<<endl;
}
