常见的排序算法总结
目录
插入排序
直接插入排序
希尔排序
选择排序
选择排序
堆排序
交换排序
冒泡排序
快速排序
归并排序
排序算法总结
排序即使一串记录按照其中某个或某些关键字的大小,递增或递减的排列起来的操作。排序这块所说的稳定性就是指,在排序前相同的数据的顺序在排序后依然保持这个顺序,如果排序前后这个顺序没有发生改变,就说明这个排序算法是稳定的,反之不稳定。
常见的排序算法可以分为:插入排序(直接插入排序、希尔排序)、选择排序(选择排序、堆排序)、交换排序(冒牌排序、快速排序)、归并排序。
插入排序
直接插入排序
直接插入排序即将待排记录按其关键码的值逐个插入到已经排好序的有序序列中,直到所有的记录插入完为止。插入排序的空间复杂度为O(1),平均时间复杂度为O(n^2),最坏时间复杂度是O(n^2),也就是待排序列为逆序的情况,最好的时间复杂度是O(n),也就是待排序列为要排的顺序时,它是稳定的排序算法。
public class InsertSort {private static void insertSort(int[] nums) {if (nums == null || nums.length == 0) {return;}for (int i = 1; i < nums.length; i++) { // 待排序列int j = i - 1;int tmp = nums[i];for (; j >= 0; j--) { // 有序序列if (tmp < nums[j]) {nums[j + 1] = nums[j];} else {break;}}nums[j + 1] = tmp;}}public static void main(String[] args) {int[] nums = {6,5,4,4,3,1,2,10,8};insertSort(nums);for (int num : nums) {System.out.print(num + " ");}}
}希尔排序
希尔排序是在直接插入排序基础上做的进一步优化。它是将待排序列按照指定距离分为若干个组,然后对每个组分别进行直接插入排序,当指定距离为1时,排序结束。
此处这个指定距离gap的取法有很多种,我们按照gap = n / 2这种方式来进行取值,每一轮结束后gap /= 2,直到gap == 1为止。
希尔排序的空间复杂度为O(1),是不稳定的排序算法,其时间复杂度最好的情况下是O(n),最坏的情况是O(n^2),平均时间复杂度是O(n^1.3)。
public class ShellSort {public static void shellSort(int[] nums) {if (nums == null || nums.length == 0) {return;}int gap = nums.length / 2;while (gap >= 1) {shell(nums, gap);gap /= 2;}}public static void shell(int[] nums, int gap) {for (int i = gap; i < nums.length; i++) { // 待排序列int j = i - gap;int tmp = nums[i];for (; j >= 0; j -= gap) { // 有序序列if (nums[j] > tmp) {nums[j + gap] = nums[j];} else {break;}}nums[j + gap] = tmp;}}public static void main(String[] args) {int[] nums = {6,5,4,4,3,1,2,10,8};shellSort(nums);for (int num : nums) {System.out.print(num + " ");}}
}选择排序
选择排序
选择排序(以升序为例)即每次从待排序列中选则最小的一个待排元素放在序列起始位置,直到所有待排序元素排完为止。选择排序的平均时间复杂度、最好时间复杂度、最坏时间复杂度都是O(n^2),空间复杂度为O(1),是不稳定的排序算法。
public class SelectSort {public static void selectSort(int[] nums) {if (nums == null || nums.length == 0) {return;}for (int i = 0; i < nums.length; i++) {int minIndex = i; // 记录最小值的下标for (int j = i; j < nums.length; j++) {if (nums[minIndex] > nums[j]) {minIndex = j;}}int tmp = nums[minIndex];nums[minIndex] = nums[i];nums[i] = tmp;}}public static void main(String[] args) {int[] nums = {6,5,4,4,3,1,2,10,8};selectSort(nums);for (int num : nums) {System.out.print(num + " ");}}
}堆排序
堆排序是指利用堆这种数据结构所设计的一种排序算法,它是选择排序的一种,它是通过堆来选择数据的。当要排升序的时候建立大根堆,排降序时建立小根堆。
以排升序为例:
1、首先我们要建立一个大根堆(如果要排降序,建立小根堆)
2、将堆顶元素与堆最后一个元素进行交换,使末尾元素最大;
3、继续调整堆,再将堆顶元素与堆最后一个元素进行互换,得到第二大元素;
4、重复2和3操作,直到end==0,结束排序。
堆排序是不稳定的排序算法,其空间复杂度为O(1),时间复杂度为O(nlog2n)。
public class HeapSort {private static void heapSort(int[] nums) {if (nums == null || nums.length == 0) {return;}// 1、创建大根堆createHeap(nums);// 堆排序int end = nums.length - 1;while (end > 0) {swap(nums, 0, end);shiftDown(nums, 0, end);end--;}}private static void createHeap(int[] nums) {for (int parent = (nums.length - 2) / 2; parent >= 0; parent--) { // 确保从最后一个非叶子结点开始向下调整shiftDown(nums, parent, nums.length);}}private static void shiftDown(int[] nums, int parent, int len) {int child = parent * 2 + 1; // 通常指向的是当前结点的左孩子while (child < len) {if (child + 1 < len && nums[child] < nums[child + 1]) { // 确保child指向的是两个节点中最大的那个child++;}if (nums[parent] < nums[child]) {swap(nums, parent, child);parent = child;child = 2 * parent + 1;} else {break;}}}private static void swap(int[] nums, int left, int right) {int tmp = nums[left];nums[left] = nums[right];nums[right] = tmp;}public static void main(String[] args) {int[] nums = {6,5,4,4,3,1,2,10,8,9,9,9,9};heapSort(nums);for (int num : nums) {System.out.print(num + " ");}}
}交换排序
冒泡排序
冒泡排序是一种简单的排序算法,它重复的遍历数组,每次比较两个元素,按照规定的排序规则将其排序,当数组已经有序时,排序结束.冒泡排序无论数组是否有序都会遍历一遍数组。其平均时间复杂度为O(n^2),最好时间复杂度为O(n),最坏时间复杂度为O(n^2),空间复杂度为O(1),是稳定的排序算法。
public class BubbleSort {public static void bubbleSort(int[] nums) {if (nums == null || nums.length == 0) {return;}for (int i = 0; i < nums.length; i++) {int flag = 0;for (int j = 0; j < nums.length - i - 1; j++) {if (nums[j] > nums[j + 1]) {int tmp = nums[j];nums[j] = nums[j + 1];nums[j + 1] = tmp;flag = 1;}}if (flag == 0) {break;}}}public static void main(String[] args) {int[] nums = {6,5,4,4,3,1,2,10,8};bubbleSort(nums);for (int num : nums) {System.out.print(num + " ");}}
}快速排序
任取待排序元素序列中的某元素作为基准值,按照该排序码将待排序集合分割成两子序列,左子序列中所有元素均小于基准值,右子序列中所有元素均大于基准值,然后最左右子序列重复该过程,直至所有元素都排列在相应位置上为止。快速排序是不稳定的排序算法,其空间复杂度为O(log2n),其平均时间复杂度为O(log2n),
public class QuickSort {public static void quickSort(int[] nums, int start, int end) {if (start >= end) {return;}int pivot = partition(nums, start, end);quickSort(nums, start, pivot - 1);quickSort(nums, pivot + 1, end);}private static int partition(int[] nums, int left, int right) {int tmp = nums[left];while (left < right) {// 从右边找到第一个比它小的值while (left < right && nums[right] >= tmp) {right--;}nums[left] = nums[right];// 从左边找第一个大于它的值while (left < right && nums[left] <= tmp) {left++;}nums[right] = nums[left];}nums[left] = tmp;return left;}public static void main(String[] args) {int[] nums = {6,5,4,4,3,1,2,10,8};quickSort(nums, 0, nums.length - 1);for (int num : nums) {System.out.print(num + " ");}}
}归并排序
归并排序是建立在归并操作上的一种有效的排序算法,该算法是采用分治法的一个经典应用。将已有序的子序列合并,得到完全有序的序列;先使每个子序列有序,再使子序列段间有序。归并排序的时间复杂度为O(nlog2n),空间复杂度是O(n),是稳定的排序算法。
public class MergeSort {private static void mergeSort(int[] nums, int left, int right) {if (left >= right) {return;}int mid = (left + right) / 2;mergeSort(nums, left, mid);mergeSort(nums, mid + 1, right);merge(nums, left, right, mid);}private static void merge(int[] nums, int left, int right, int mid) {int[] tmp = new int[right - left + 1];int s1 = left;int e1 = mid;int s2 = mid + 1;int e2 = right;int k = 0;while (s1 <= e1 && s2 <= e2) { // 两个归并段都有数据if (nums[s1] <= nums[s2]) { // <= 确保了它是稳定的排序算法tmp[k++] = nums[s1++];} else {tmp[k++] = nums[s2++];}}while (s1 <= e1) {tmp[k++] = nums[s1++];}while (s2 <= e2) {tmp[k++] = nums[s2++];}for (int i = 0; i < k; i++) {nums[i + left] = tmp[i];}}public static void main(String[] args) {int[] nums = {6,5,4,4,3,1,2,10,8};mergeSort(nums, 0, nums.length - 1);for (int num : nums) {System.out.print(num + " ");}}
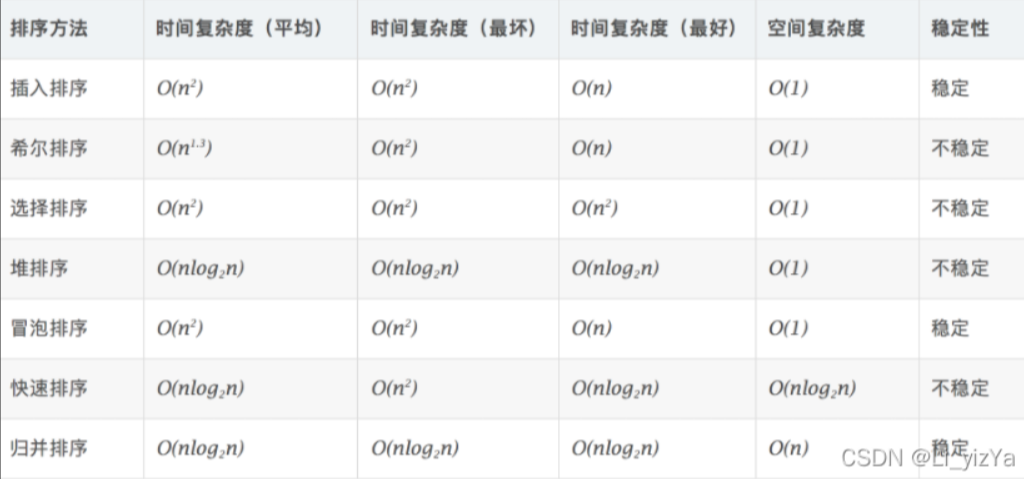
}排序算法总结
稳定性:上述的七大排序算法中,其中归并排序、插入排序、冒泡排序是稳定的排序算法;选择排序、希尔排序、堆排序、快速排序是不稳定的排序算法。
空间复杂度:冒泡排序、插入排序、希尔排序、选择排序、堆排序的空间复杂度是O(1),快速排序的空间复杂度是O(nlog2n),归并排序的空间复杂度为O(n)。
时间复杂度:以平均时间复杂度来看,冒泡排序、插入排序、选择排序的平均时间复杂度是O(n^2),希尔排序的平均时间复杂度是O(n^1.3),归并排序、快速排序、堆排序的平均时间复杂度是O(nlog2n)。