当前位置：首页 > news >正文

[优化算法]神经网络结构搜索（一）

news 2025/9/10 6:50:26

一、概述

神经网络主要由两类数据构成：参数(Parameters)和超参数(Hyper-Parameters)。其中参数即需要从训练数据中学习，并进行更新的数据，如卷积核中的参数；超参数则分为两类：结构超参数(Architecture)和算法超参数(Algorithm)，其中结构超参数具体表现在一个神经网络有多少层、每层有多少卷积核、每个卷积核的尺寸等；算法超参数则体现在使用的迭代算法，如SGD或Adam。

以CNN为例，结构超参数可以分为以下三种：

①卷积层(Conv)的数量和全连接层(Dense)的数量

②每个卷积层中的卷积核数量、大小和步长

③每个全连接层的宽度

神经网络结构搜索(Neural Architecture Search, NAS)：指使用算法找到最优的神经网络结构超参数，是的模型在验证集上的精度最高。

搜索空间(Search space)：搜索空间是一组包含所有神经网络可能结构的集合，是用户事先制定的。

通过NAS的选择，得出的搜索结果（结构超参数）如下所示：

二、随机搜索

通过不断重复：选择结构超参数->构建神经网络->进行验证。这三个步骤，选择验证结果中最佳的有种作为最佳结构超参数，这个过程是随机的，如下图所示。

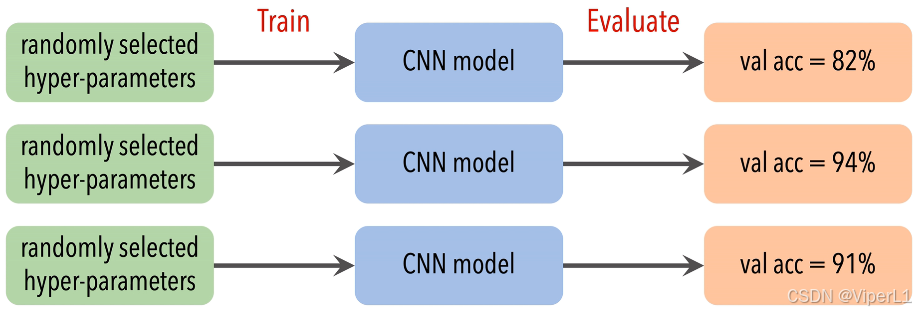
随机搜索虽然实现简单，但是依旧存在以下问题：

①优化开销巨大：每次选择超参数后，需要单独进行建模，并从零开始对这个模型进行训练。

②搜索空间巨大：由于各模块的组合多样性，NAS并不能完整的穷举整个搜索空间。

三、循环神经网络+强化学习

3.1 控制器RNN的构型

使用RNN生成一个CNN，可以分为以下几步：

①对于RNN的初始状态 $h_0$ （全0）和输入 $x_0$ （随机生成），通过RNN处理后输出一个向量 $h_1=tanh(W\begin{bmatrix} h_0\\ x_0 \end{bmatrix}+b)$ ，如下图。

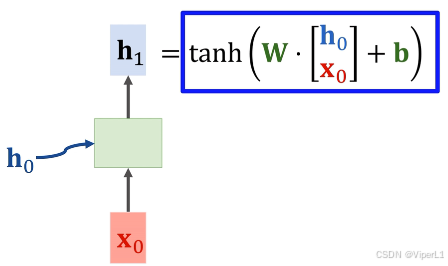
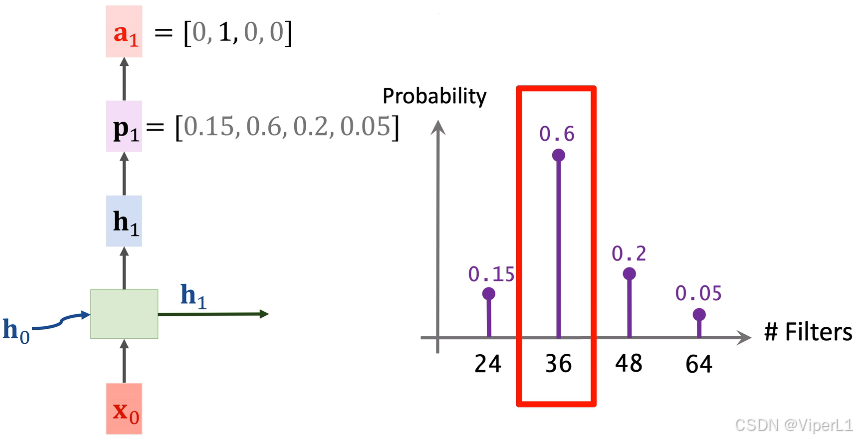
②将 $h_1$ 输入一个softmax分类器，输出记作 $p_1$ ， $p_1$ 为第一层卷积核个数的概率预测（需要提前指定几个可选项），并使用随机选择(random)或最大值选择(argmax)选出一个值，将这个值记作one-hot向量 $a_1$ ，如下图；在这里模型预测的内容为卷积核个数，可选项为24,36,48,64这4个。

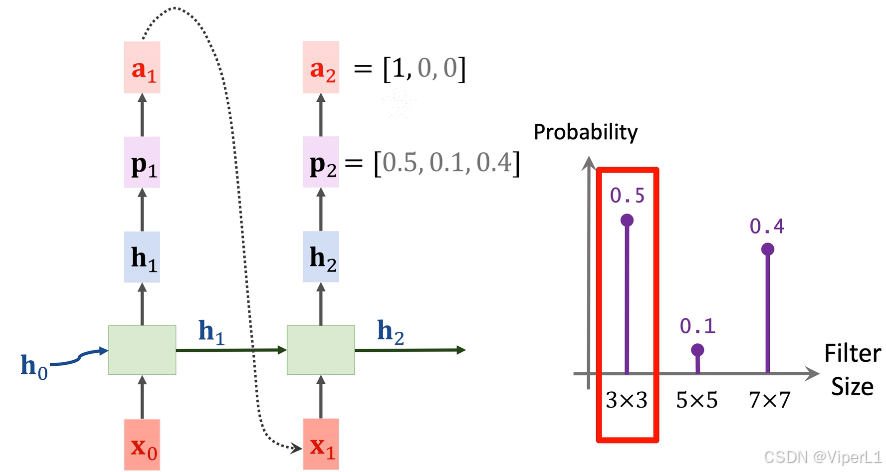
③利用嵌入层(Embedding)将 $a_1$ 映射为一个稠密向量 $x_1$ ，再将向量 $h_1$ 作为状态，向量 $x_1$ 作为输入，使用RNN计算出向量 $h_2$ ；再将向量 $h_2$ 的拷贝作为下一时刻的状态，同时使用softmax分类器将 $h_2$ 映射为概率 $p_2$ ，进一步使用softmax选择一个值，记作one-hot向量 $a_2$ 。如下图；在这里模型预测的是卷积核尺寸，可选项为3x3,5x5,7x7这三个，需要注意的是，由于输出维度和任务均不相同，此处的softmax与步骤②并不复用。

Ps.虽然这些softmax不能复用，但嵌入层在相同的任务中是可以复用的。同时由于RNN要求输入向量的维度一致，所以映射后的向量 $x_i$ 的维度需要保持一致。

④接下来重复步骤③的操作，来预测卷积步长。如下图；

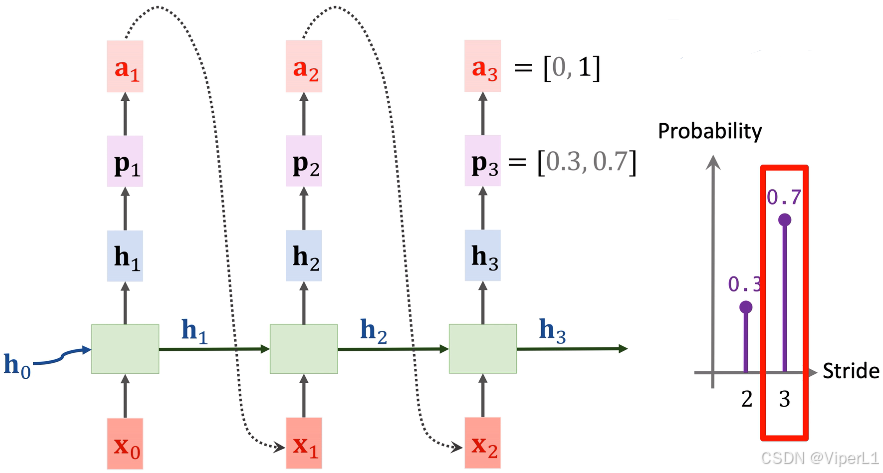
通过不断重复上述步骤，即可得到一个模型的所有结构超参数，以一个20层的模型为例，每三个超参数可以确定一个卷积层（卷积核个数，卷积核尺寸，步长），用来生成超参数的RNN被称为控制器RNN(Controller RNN)。

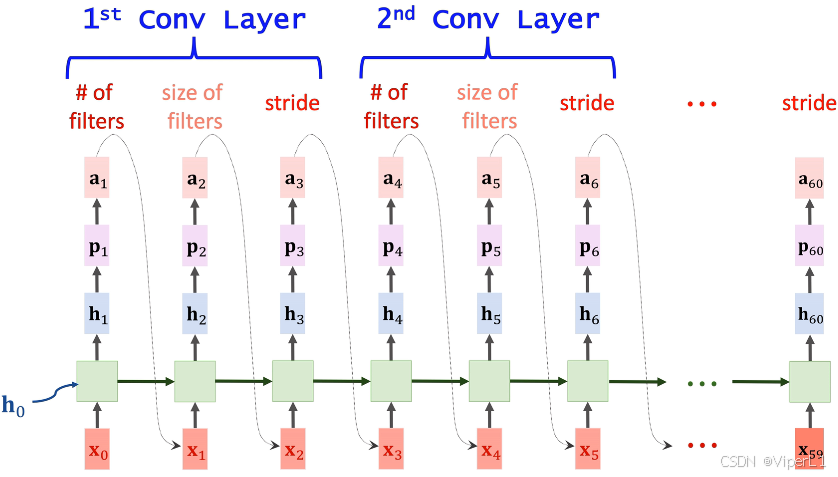
3.2训练控制器RNN

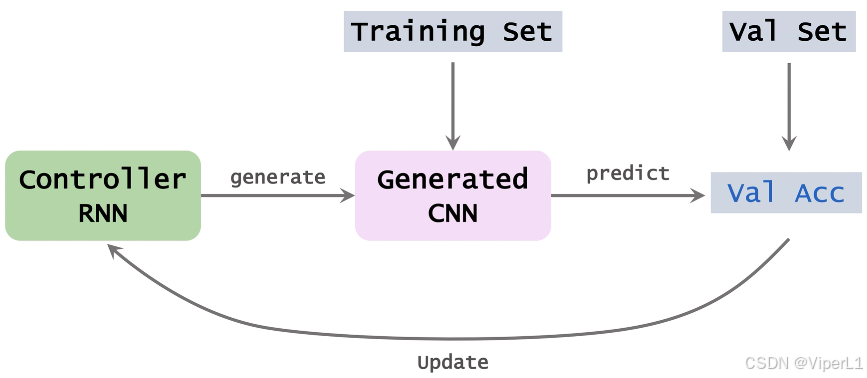
要训练一个控制器RNN需要以下几步，同时如下图所示：

①使用控制器RNN生成一组CNN的结构超参数。

②根据步骤①的结构超参数实例化一个CNN。

③使用数据集训练步骤②搭建的神经网络

④对步骤③训练好的数据集进行预测，得到平均准确率

⑤使用步骤④的平均准确率更新控制器RNN，控制器RNN更新的目标是让平均准确率更高。

实现上述步骤还存在一个问题：即目标函数 $r$ 必须对于参数 $\theta$ 可微，才可以将其计算为梯度形式： $\theta\leftarrow \theta+\beta \frac{\alpha r}{\partial \theta}$ 。在上述问题中，目标函数 $r$ 为CNN的平均准确率，但优化参数 $\theta$ 是控制器RNN的参数，两者并不构成可微关系，所以无法直接使用反向传播更新RNN。为了解决这个问题，引入强化学习。强化学习并不要求 $r$ 和 $\theta$ 之间可微，直接将不可微的目标作为环境奖励。

3.3使用强化学习训练控制器RNN

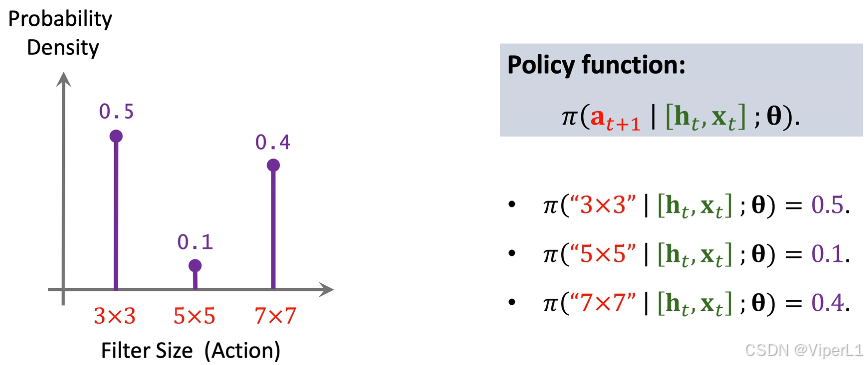
对于整个强化学习而言：奖励(Rewards)是CNN的平均准确率，策略函数(Policy Function)为控制器RNN，使用策略梯度上升来更新策略函数。

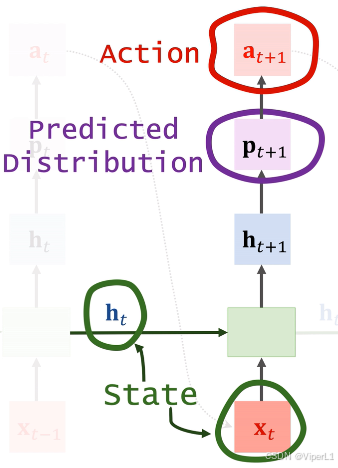
对于策略函数 $p_{t+1}=\pi(a_{t+1}|[h_t,x_t];\theta)$ 而言， $p_{t+1}$ 为策略函数输出的概率分布， $a_{t+1}$ 为动作（离散的）， $h_t$ 到 $x_t$ 为状态。

以第60步为例，前59步的奖励不可见，记作 $r_1=r_2=...r_{59}=0$ ；第60步的奖励记作 $r_{60}=ValAcc$ ；将 $t$ 时刻的回报记作 $u_t$ ， $u_t=r_t+r_{t+1}+r_{t+2}+...r_{59}+r_{60}$ ，故 $u_1=u_2=...=u_{60}=ValAcc$ 。

通过上面的推导，第 $t$ 步的近似策略梯度函数可以写作： $\frac{\partial log_\pi(a_{t+1}|[h_t,x_t];\theta)}{\partial \theta}u_t$

通过对策略梯度求和可以用来更新参数： $\theta\leftarrow \theta+\beta \sum_{t=1}^{60} \frac{\partial log_\pi(a_{t+1}|[h_t,x_t];\theta)}{\partial \theta}u_t$ ，其中 $\beta$ 为手动设置的学习率参数。